“用油膜法估测分子大小”改编题型中的科学性错误
“用油膜法估测分子大小”改编题型中的科学性错误
庄勇飞
(江苏省锡山高级中学江苏 无锡214174)
摘 要:“用油膜法估测分子大小” 可以把油酸分子简化为球形,测出油膜的厚度d,就认为是油酸分子的直径,这只是在估测油酸分子大小的数量级时的简化处理,而对于其直径数值的估算,偏差是非常大的,通过下面的几个例子可以看出,我们不应该将这种简化的模型来处理更多的计算,特别是对基本物理学常数——阿伏伽德罗常数的计算.
关键词:估测数量级计算
收稿日期:(2015-05-19)
估测法是利用物理概念、规律、物理常数和常识对物理量的数值、数量级以及取值范围合理估测的近似方法[1].“用油膜法估测分子大小”,是最早测量分子大小的一种方法.自1997年开始使用的全日制高级中学物理教科书开设该实验以来,各种版本的教材中都保留了该实验.该实验利用的用宏观量来测量微观量的实验方法是科学研究的重要方法之一,该实验又是高中物理学生实验中唯一体现该方法的实验.学生在认识微观世界的过程中,对分子直径的数量级有了清晰的感性认识,进一步认识了物理模型在物理研究中的重要价值,启迪学生处理微观问题的思路,为正确解决关于微观世界的实际问题做了铺垫.
人教版《物理·选修3-3》第七章第1节中对“怎样估算油酸分子的大小”做了详细的论述:“把很小一滴油酸滴在水面上,水面上会形成一块油酸薄膜,薄膜是由单层的油酸分子组成的.尽管油酸分子有着复杂的结构和形状,但在估测其大小的数量级时,可以把它简化为球形,示意图如图1所示.测出油膜的厚度d,就是油酸分子的直径.”[2]
这段话中有一个非常关键的点“在估测其大小的数量级时”,也就是说,该种模型的处理方法对数量级的估测是没有问题的,但对粗略测定油酸分子的直径,会出现较大的偏差.
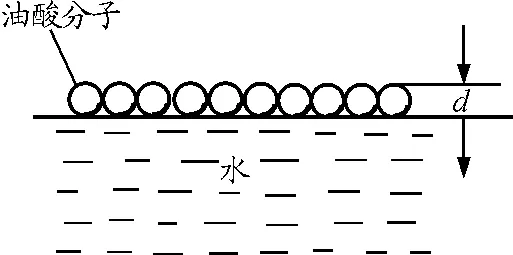
图1
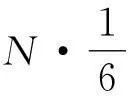
在2013年某地的高考模拟试卷上有这样一个问题:用单分子油膜法测出油酸分子(视为球形)直径后,还需要下列哪一个物理量就可以计算出阿伏伽德罗常数
A.油滴的体积
B.油滴的质量
C.油酸的摩尔体积
D.油酸的摩尔质量
从纯粹计算上说,知道了摩尔体积当然就能算出阿伏伽德罗常数,但正如笔者前面所说,油膜法估测的只是分子直径的数量级,而在测算分子大小上面偏差较大,所以用该数据计算出来的阿伏伽德罗常数必然偏差也较大,只能保证其在数量级上准确而已,笔者认为,阿伏伽德罗常数作为一个物理学中非常重要的常数,就算我们要近似计算其数值,也不应该有太大的偏差,何况是偏离实际值30%以上.因此根本就不应该用这样的方法来求阿伏伽德罗常数,这对学生是一种不科学的引导.
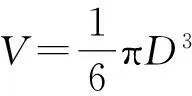
我们不妨从另一个角度来考虑这个问题,油膜的面积当然也可以是分子总个数与每个分子截面积的乘积,即
计算得
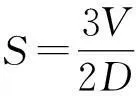
作为一个高考题,正是因为编者对油膜法的相关计算采用了常规化的思考方式,而没有考虑到其他非常规的求解法,致使本题有两个不同的答案,就算题中要求保留一位有效数字,依然未能化解两个答案的不同,由此也可知,油膜法估测在数值上的偏差之大.
更有甚者,在许多教辅材料中,有选编了某地的模拟考试题:利用单分子油膜法可以粗测分子的大小和阿伏加德罗常数,如果已知体积为V的一滴油在水面上散开形成的单分子油膜的面积为S,这种油的摩尔质量为M,密度为ρ,则阿伏加德罗常数NA可表示为?
本题给出的标准解答是
得
但是,我们班上也有好多学生做出来是
得
通过上述几个例子的分析,我们可以看到,我们对于一种方法的理解和应用,首先应该是正确理解课本,从课本所给出的科学定义出发,而不要随意的对其改编,最后变得曲解了课本的原意,扭曲了科学的事实.
参 考 文 献
1冯杰. 高中物理探究实验及案例教学设计. 北京:北京大学出版社,2011. 139
2普通高中课程标准实验教科书.物理·选修3-3.北京:人民教育出版社,2010.2

