均值不等式在高中物理解题中的应用

均值不等式在高中物理解题中的应用*

杨绍林

(云南师范大学物理与电子信息学院云南 昆明650500；

昆明一中度假区分校金岸中学云南 昆明650031)

彭朝阳

(云南师范大学物理与电子信息学院云南 昆明650500)

中学物理实验教学研究教学案例建设，编号：YJG2014-A05

摘 要：运用数学工具解决物理问题，是高考考查学生能力的方式之一，而高中物理问题中常出现求极值问题，如：最长、最大、最短、至少、最多等．这些问题渗透在物理中的运动学、力学、电磁学和电学等问题中．均值不等式是求解极值问题有效的方法，分为定和求积与定积求和两种形式．在物理解题中有许多极值题可以构造出定和或定积的形式，进而求出最大值或最小值．

关键词：极值问题均值不等式定和求积定积求和

作者简介：杨绍林(1985-)，男，在读硕士研究生.

通讯作者：彭朝阳(1971-)，男，教授，主要从事物理教育教学研究.

收稿日期：(2015-05-26)

每年各种各样的高考模拟题、高考仿真卷、高考试题中，出现用均值不等式解题的极值问题较多，所以教师在平时的教学中应该多渗透用均值不等式来求解，不仅省时省力，学生用数学工具解决物理问题的能力也会得到提高．

但现在教师们多数停留在普通的数学求解和单纯的解题，没有把物理思想和解题规律进行融合和归纳总结，使得学生不得解极值问题的精髓．就这些问题，下面例举一些均值不等式的应用，以期加深对此类问题的理解．

1均值不等式在高考模拟题中的应用

【例1】如图1半径为R的半圆形光滑凹槽固定，质量为m的小球Q，从最高点A运动至B的过程中，在什么位置重力做功的功率最大？最大值是多少？

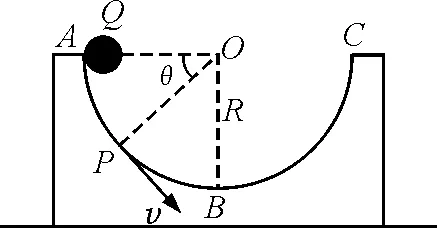
图1

解析：设小球Q运动到A与B间某位置P时，半径OP与水平方向成θ角，此时瞬时速度为v，则此时重力的瞬时功率为

P=mgvcosθ

(1)

由机械能守恒定律的

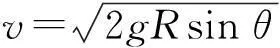
(2)

将式(2)代入式(1)得

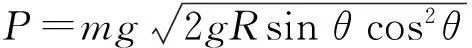
(3)

此时问题转化为求极值

y=sinθcos2θ

(4)

将式(4)做数学变形如下

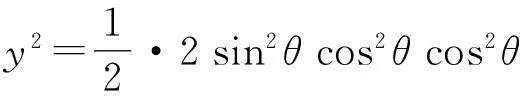
(5)

由均值不等式得

(6)

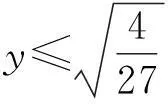
(7)

将式(7)代入式(3)得

(8)

【例2】如图2所示，R1=2 Ω，R2=3 Ω，滑动变阻器的最大阻值R3=5 Ω，则在滑片从a端滑到b端的过程中，电流示数的最小值为多少？

图2

解析：设滑片上部分电阻为Rx，则下部分电阻为(5-Rx) .

电路的总电阻为

利用均值不等式

(2+Rx)(8-Rx)≤

当(2+Rx)=(8-Rx)时，即Rx=3 Ω时，R最大，电流表的示数最小．此时

电流表示数

本题的极值问题也是属于均值不等式的“定和求积问题”，即(2+Rx)和(8-Rx)的和是定值，那么(2+Rx)(8-Rx)必有最大值[1]．

【例3】如图3所示，已知电源电动势为E，内阻为r，开关S闭合后，求R为多大时，电源输出功率有最大值 ?

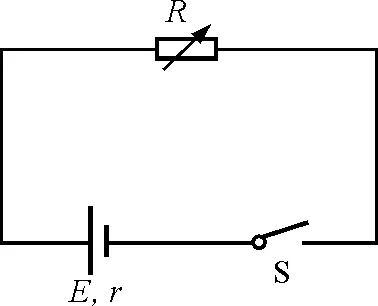
图3

解析：由题意可知，电源的输出功率最大值为

由均值不等式可知

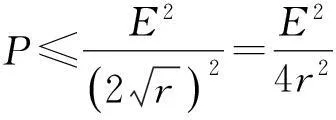
2均值不等式在高考仿真卷中的应用

【例4】如图4所示，AOC是光滑的直角金属导轨，AO沿竖直方向，OC沿水平方向，ab是一根金属直棒，如图立在导轨上，b端比a端更靠近O点．它从静止开始在重力作用下运动，运动过程中b端始终在OC上，a端始终在AO上，直到ab完全落在OC上．整个装置放在一匀强磁场中，磁场方向垂直纸面向里，则ab棒在运动过程中

A．感应电流方向始终是b→a

B．感应电流方向先是b→a，后变为a→b

C．棒受磁场力方向与ab垂直，如图中箭头所示方向

D．棒受磁场力方向与ab垂直，开始如图中箭头所示方向，后来变为与箭头所示方向相反

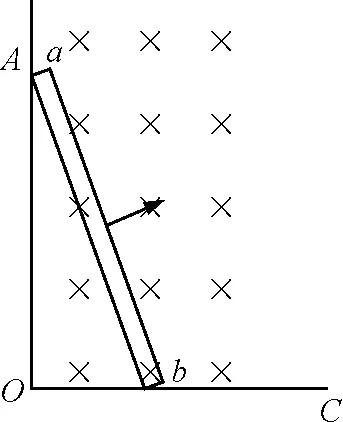
图4

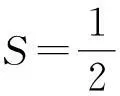
本题属于均值不等式的“定和求积问题”，但根据均值不等式原理可知，这题两个变量相等时，它们的乘积有最大值[2]．

【例5】水平传送带以2 m/s的速度做匀速直线运动，传送带的两端距离为2 m，将一物体轻轻放在传送带的一段，物体由一端运动到另一端经历的时间为11 s，则物体与传送带之间的动摩擦因数是多少？(g=10 m/s)要求物体从传送带一端A运动到另一端B用时最短？

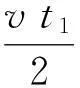
t1+t2=11

v=μgt1

联立以上各式得

μ=0.1

由于物体先匀加速再匀速运动，则运动的总时间

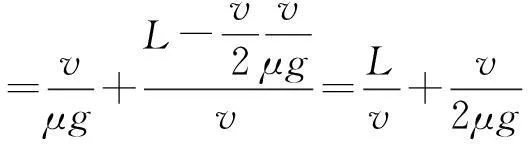
由均值不等式可知

3均值不等式在高考真题中的应用

【例6】(2010年高考江苏卷第14题)在游乐节目中，选手需借助悬挂在高处的绳飞越到水面的浮台上，小明和小阳观看后对此进行了讨论如图5所示，他们将选手简化为质量m=60 kg的质点，选手抓住绳由静止开始摆动，此时绳与竖直方向夹角α=53°，绳的悬挂点O距水面的高度为H=3 m，不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深，取重力加速度g=10 m/s2，sin53°=0.8，cos53°=0.6．若选手摆到最低点时松手，小明认为绳越长，在浮台上的落点距岸边越远；小阳却认为绳越短．落点距岸边越远请通过推算说明你的观点．

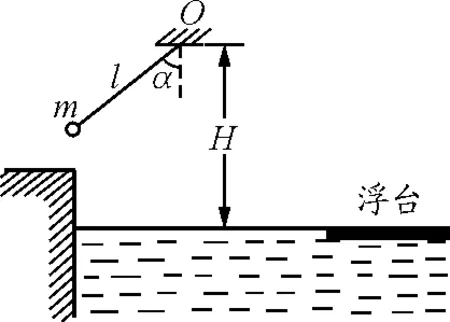
图5

分析：由圆周运动知识可知最低点松手时的速度，再由平抛运动可知水平位移的表达式，进而找到绳长与落点的关系．

解析：设选手从最低点开始做平抛运动速度为v，设浮台上的落点距岸边水平距离为x，平抛时间为t，则

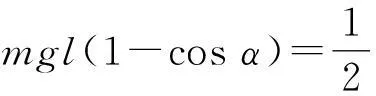
x=vt

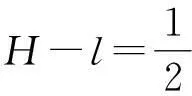
由以上各式解得

利用均值不等式

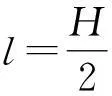
本题中的极值问题是属于均值不等式中的“定和求积问题”，即l和H-l的和是定值，那么l(H-l)必有最大值．

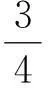
(1)求绳断时球的速度大小v1，和球落地时的速度大小v2；

(2)问绳能承受的最大拉力多大；

(3)改变绳长，使球重复上述运动．若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？

图6

解析：根据机械能守恒和动能定律可知，第(1)、(2)问中的解为

(3)设绳长为l,绳断时球的速度大小为v3,绳承受的最大拉力不变，有

得

绳断后球做平抛运动，竖直位移为d-l,水平位移为x，时间为t1.有

x=v3t1

由上式得

又由均值不等式得

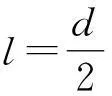
本题中的极值问题是属于均值不等式中的“定和求积问题”，即l和d-l的和是定值，那么l(d-l)必有最大值[4]．

综上所述，均值不等式是处理物理问题的重要工具，在平时的物理教学过程中，教师不仅应善于利用均值不等式来分析和处理物理问题，还要引导学生总结使用它的方法和技巧，丰富高中学生的知识逐步培养学生利用均值不等式来处理物理问题的习惯和能力．

参 考 文 献

1李海平、张瀚泽．高考模拟试题汇编.拉萨：西藏人民出版社，2013.10～17

2谢兆刚．全国各省市高考试题汇编．合肥：安徽教育出版社，2014.40～47

3魏万青．金版教程.兰州：甘肃教育出版社，2016.59

4曲一线．5年高考真题详解．北京：首都师范大学出版社，2010.6～10