磁场下椭圆形量子线中电子与空穴的基态能量

磁场下椭圆形量子线中电子与空穴的基态能量

段秀芝1，王广新2，常春蕊2

(1.华北理工大学 轻工学院，河北 唐山063000；2.华北理工大学 理学院，河北 唐山063000)

摘要：采用单电子近似方法求解薛定谔方程，研究了椭圆形量子线中电子和空穴的基态能量及其受磁场的影响.详细描述了能量哈密顿算符在原子单位与国际单位之间的换算及处理粒子有效质量失配及空穴有效质量各向异性的一种方法，数值结果表明，磁场的约束使得粒子的基态能量增加，粒子的基态能量随着椭圆坐标中的参数的增大而减小.本文所用的方法可推广到其他类似物理模型的薛定谔方程的求解中.

关键词：磁场；椭圆形量子线；电子；空穴

DOI：10.3969/j.issn.1000-1565.2015.05.004

中图分类号：O469文献标志码：A

收稿日期:2015-01-25

基金项目：河北省科技计划基金资助项目(12210617)；华北理工大学轻工学院科学研究基金资助项目(qy201205)

Ground-state energy of electron and hole in elliptical

quantum wire in the presence of a magnetic field

DUAN Xiuzhi1, WANG Guangxin2, CHANG Chunrui2

(1.Qinggong College, North China University of Science and Technology, Tangshan 063000, China;

2.College of Science, North China University of Science and Technology, Tangshan 063000, China)

Abstract:Schrodinger equations of electron and hole in elliptical quantum wire have been solved by using single-active electron (SAE) approximation and the ground-state energies of electron and hole affected by the magnetic field applied along x-axis have been studied. The conversion of Hamilton between atomic unit and international unit and a method of dealing with the mass mismatch of the particles and anisotropic effective mass of the hole have been represented in detail. The confine of a magnetic field makes the ground-state energy of the particles increases and the ground-state energy of the particles decreases as the parameterin elliptic coordinate increases. The method used in this paper can be extended to the study of solving Schrodinger equation in other similar physical models.

Key words: magnetic field; elliptical quantum wire; electron; hole

第一作者：段秀芝(1982-)，女，河北邢台人，华北理工大学讲师，主要从事半导体超晶格物理研究.

E-mail：duanxiuzhi2001@126.com

量子线(quantum wire,QW)是(准)一维介观纳米结构，电子和空穴的运动在2个维度上被局限在介观尺寸之内，只能在1个维度上自由运动.直到1989年才出现了一些关于量子线的实验报道.最早是采用在量子阱上再刻蚀的方法.后来出现了用分子束外延技术在各种自然表面上生长的方法，如在小偏角面、超台阶面、高指数面等，或者在由人工做出的衬底上生长，如V形槽、解理异质结构的侧面生长、在掩膜表面上的局部生长、自组织生长等[1].随后出现了大量相应的理论研究，如量子线中类氢杂质束缚能的研究[2]，V形和T形量子线中能带结构和光学各向异性的研究[3]，波函数对有限方形量子线中电子及杂质的影响[4]，InP基量子线激光器的研究[5].尹新等[6]用变分法研究了阶梯量子阱中类氢杂质的束缚能受电场的影响.郑冬梅等[7]对双电子柱形量子点系统束缚能进行了研究，其中考虑了内建电场和杂质态对束缚能的影响.丁朝华等[8]研究了磁场对量子线中束缚极化子激发态性质的影响.在理论上，人们对量子线结构中电子结构、杂质态、激子态等做了大量研究工作，并研究了外界扰动(电场、磁场、激光场等)对其物理性质的影响.本文研究了椭圆形量子线中电子和空穴的基态能量及其受到的平行于截面的磁场影响.通过对波函数展开求解薛定谔方程，考虑了电子和空穴的质量失配及空穴质量的各向异性.

1理论模型

研究的InAs/InP椭圆形截面量子线模型如图1所示，椭圆形截面在x-o-y面上，磁场沿x轴方向，z轴方向为量子线的生长方向磁场沿x轴，粒子(电子和空穴)满足的薛定谔方程为

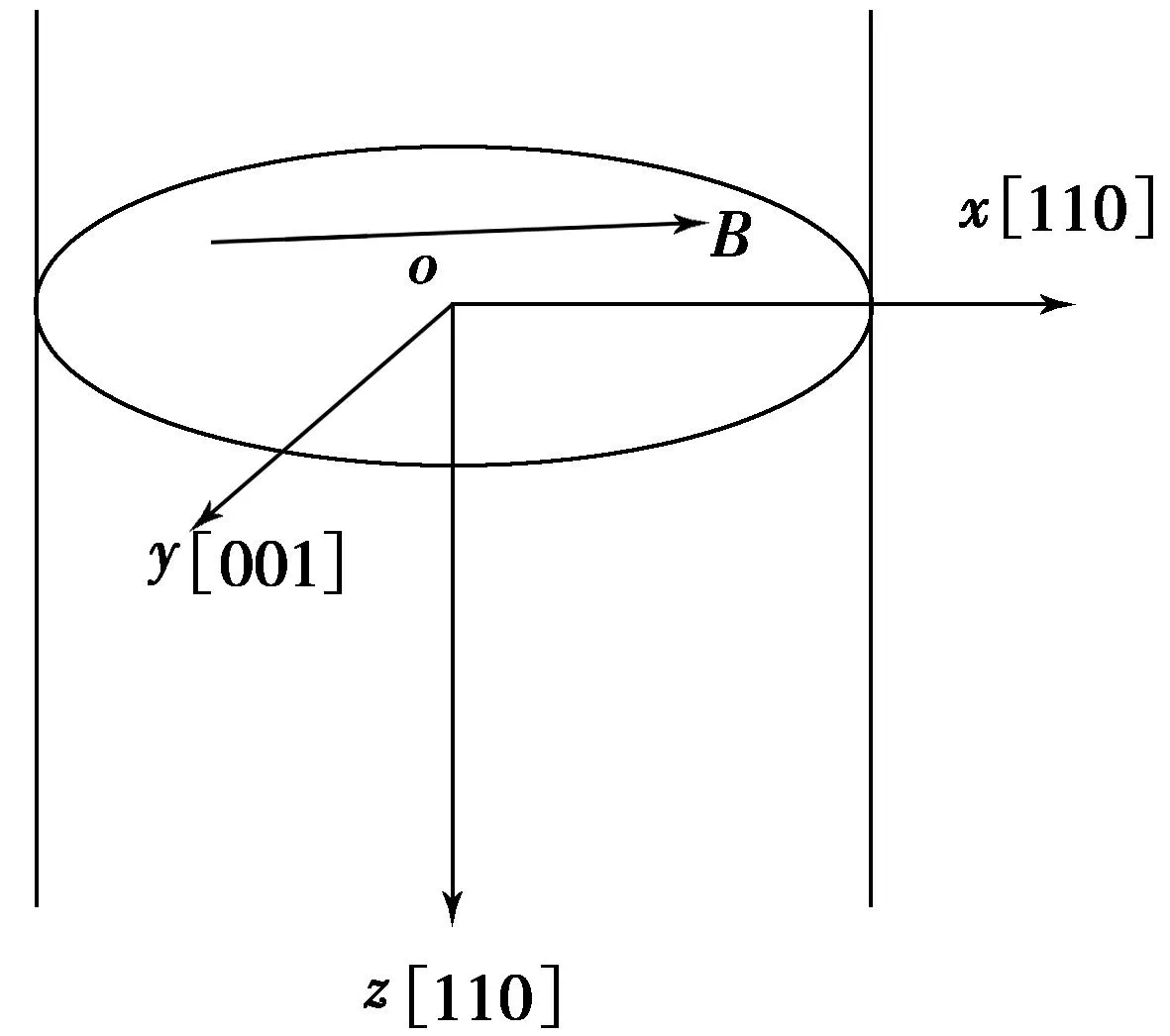
图1　椭圆形量子线 Fig.1　Cross section of a elliptical quantum wire

Ve,h(xe,h,ye,h)]ψe,h(xe,h,ye,h)=Ee,hψe,h(xe,h,ye,h)，

(1)

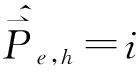
首先讨论电子基态能量的求解，电子的电量q=-e，量子线内电子的哈密顿算符为

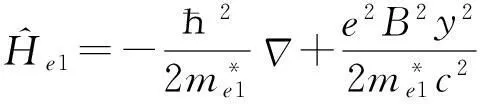
(2)

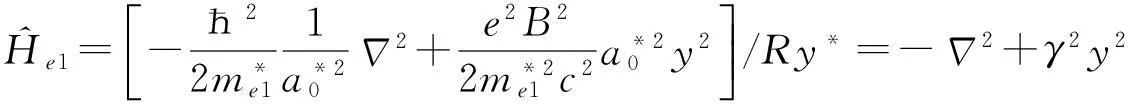
(3)

在线外，电子的哈密顿有如下形式：

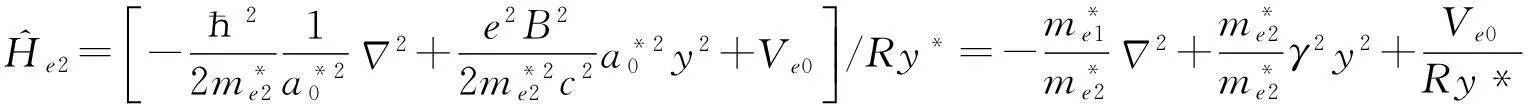
(4)

椭圆坐标和直角坐标之间的关系

x=achξcosθ；y=ashξsinθ.

(5)

在极坐标系下

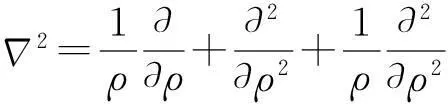
(6)

考虑到椭圆边界

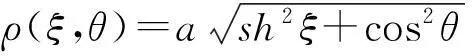
(7)

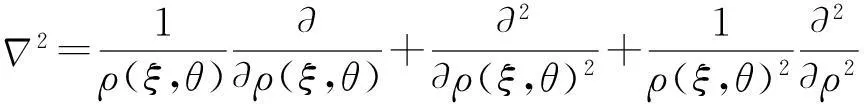
(8)

选择合流超几何函数为基函数

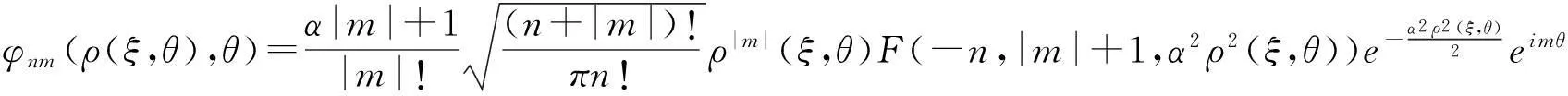
(9)

可将波函数展为如下形式

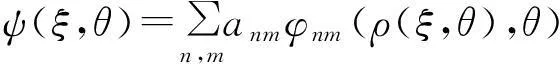
(10)

其中，anm为展开系数.通过对角化的计算方法求解微分方程，矩阵元可表示为

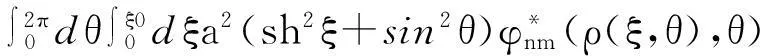
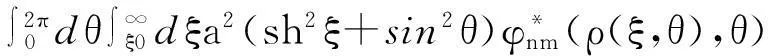
(11)

其中，a2(sh2ξ+sin2θ)为椭圆坐标的度规系数.通过在椭圆坐标系下求解久期方程可得出电子的基态能量.

求解空穴的基态能量时，空穴的带电量q=e，空穴的有效质量具有各向异性，沿着x轴、y轴取不同值，空穴在量子线内、外的有效质量也不同，取量子线内空穴沿着x轴、y轴的有效质量分别为mh1x和mh1y，量子线外空穴的有效质量沿着坐标轴的取值可描述为mh2x和mh2y，量子线内，空穴的哈密顿算符为

(12)

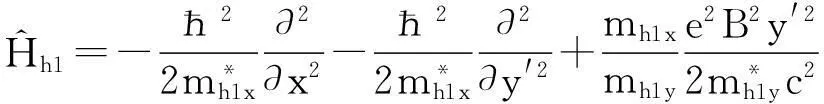
(13)

量子线外，空穴的哈密顿算符为

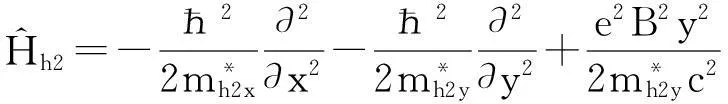
(14)

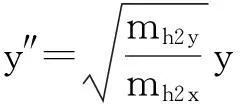
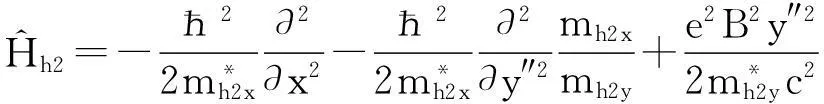
(15)

2计算与讨论

本文采用原子单位计算了电子和空穴的基态能量随量子线尺寸的变化关系及其受磁场的影响，考虑了电子和空穴的有效质量失配及空穴有效质量的各向异性.考虑到材料的晶格失配，将电子和空穴的垒高分别取为0.513和0.430 eV[9].表1为材料中的参数[10].

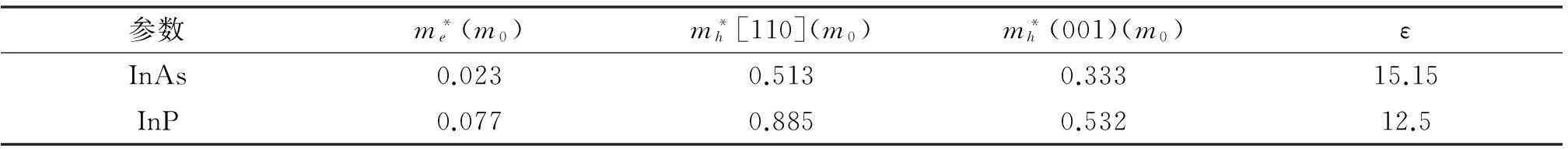
表1　InAs/InP量子线中的参数

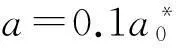
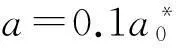
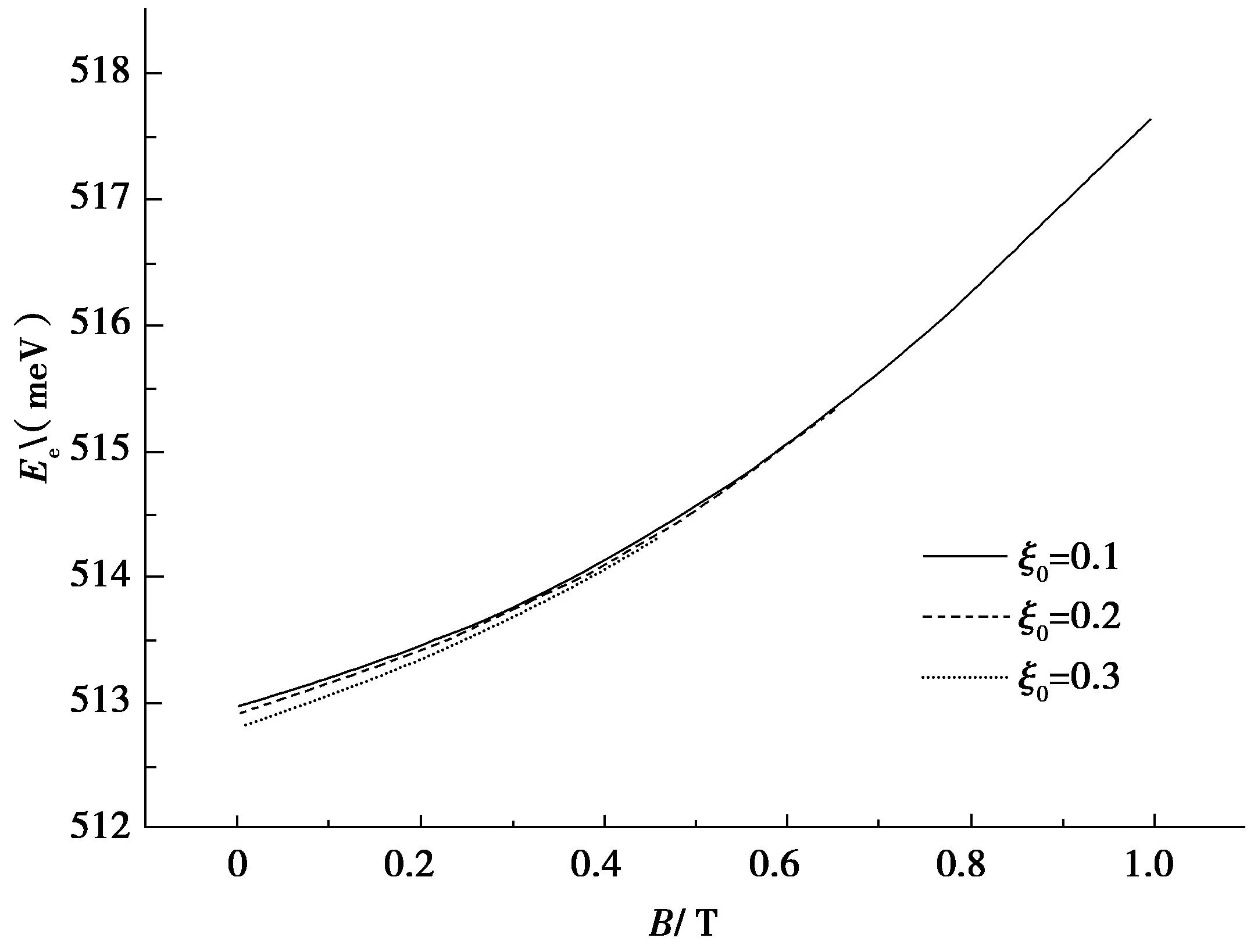
图2　椭圆形量子线中电子的基态能量随磁场的变化关系 Fig. 2　Electron ground-state energy changes with magnetic field in elliptical quantum wire

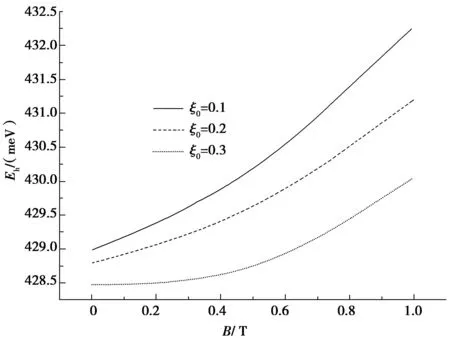
图3　椭圆形量子线中空穴的基态能量随磁场的变化关系 Fig. 3　Hole ground-state energy changes with magnetic field in elliptical quantum wire

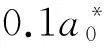
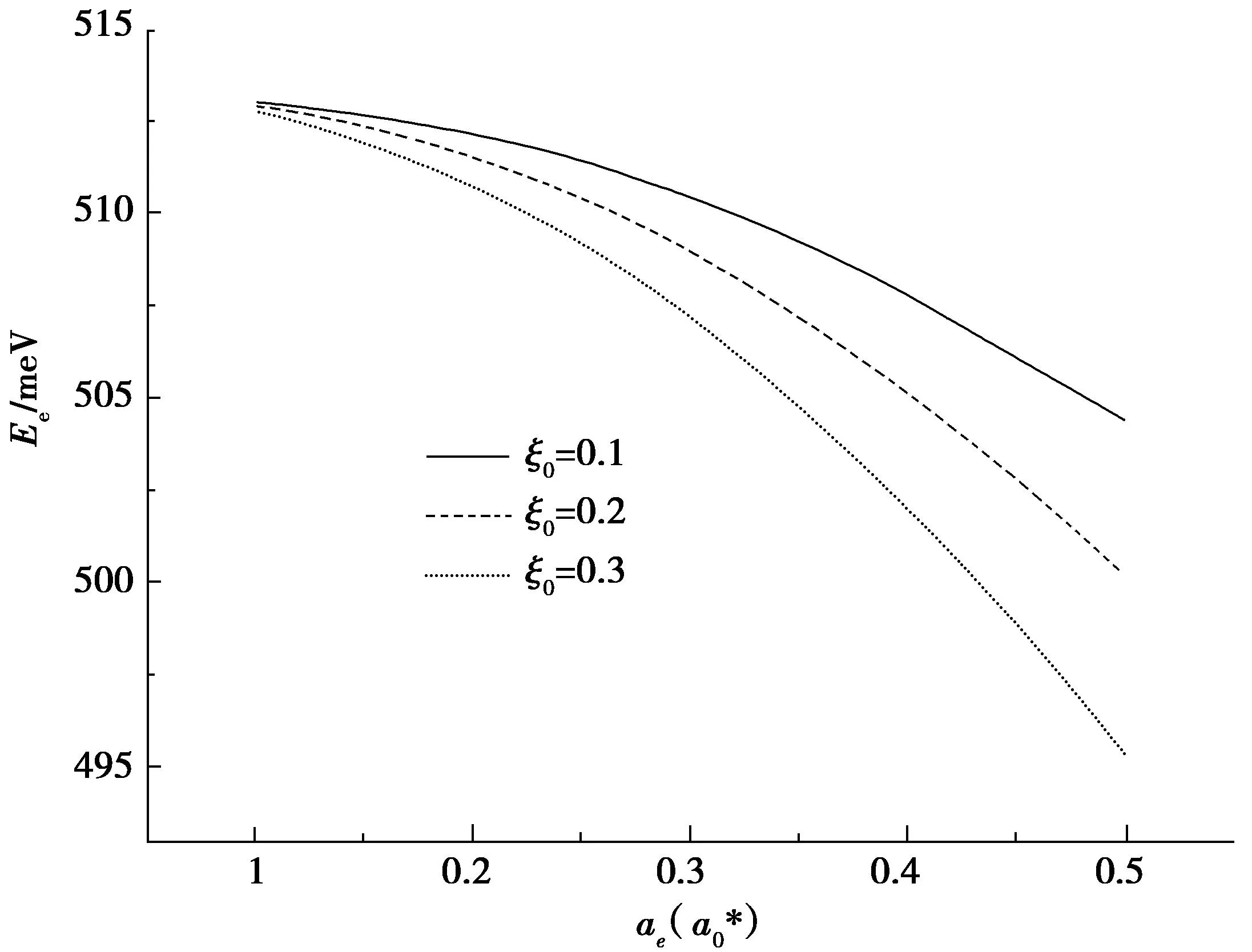
图4　椭圆形量子线中电子的基态能量随参数a e的变化关系 Fig. 4　Electron ground-state energy changes with parameter a e in elliptical quantum wire

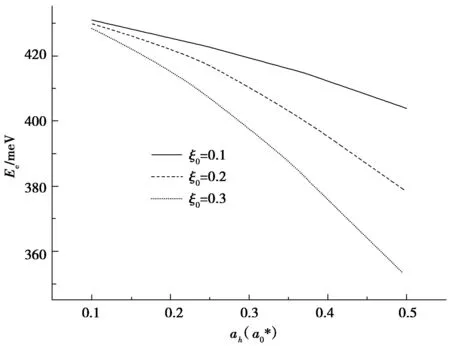
图5　椭圆形量子线中空穴的基态能量随参数a h的变化关系 Fig. 5　Hole ground-state energy changes with parameter a h in elliptical quantum wire

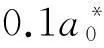
3结论

本文详细描述了原子单位与国际单位的换算过程和一种处理粒子有效质量失配及有效质量各向异性的方法，运用在椭圆形量子线中得出了规律性结论.这种方法还可以运用在其他类似物理模型的薛定谔方程求解之中.

参考文献:

[1]夏建白． 量子线、量子点和它们的激光器[J]．物理，1998, 27(3): 141-145.

煤粉储仓为伴热设备，与设备之间有伴热管线，在该情况下，为了减小伴热管由于热胀冷缩以及管道安装所产生的应力，因而在伴热管的出入口处采用了π形弯。

XIA Jianbai. Quantum wires, quantum dots and their lasers[J].Physic，1998, 27(3): 141-145.

[2]LIU Jianjun, SU Hui, GUAN Ronghua, et al. Binding energy and photoionization of hydrogenic impurities in GaAs/Ga1-xAlxAs quantum well wires[J]. Chinese Journal of Semiconductors, 2003, 24(6): 561-566.

[3]GOLDONI G, ROSSI F, MOLINARI E. Band structure and optical anisotropy in V-shaped and T-shaped semiconductor quantum wires[J]. Phys Rev B, 1997, 55(11): 7110-7123.

[4]屈双惠， 李琳艳， 杨志宏． 波函数对有限深方形量子线中电子及杂质能量的影响[J]． 宁夏大学学报：自然科学版， 2012, 33(1): 35-38.

QU Shuanghui, LI Linyan, YANG Zhihong. Effect of wave function to electron and impurity energy in square quantum well wires finite barriers[J]. Journal of Ningxia University: Natural Science Edition, 2012, 33(1): 35-38.

[5]杨新荣，徐波，赵国晴,等．InP基近红外波段量子线激光器的温度特性研究[J]． 物理学报，2012, 61(21): 216802.

YANG Xinrong, XU Bo, ZHAO Guoqing, et al. Investigation of the temperature sensitiving of the long-wavelength InP-based laser[J]. Acta Phys Sin, 2012, 61(21): 216802.

[6]尹新， 王海龙， 龚谦，等． GaInAsP/InP阶梯量子阱中氢施主杂质束缚能[J]．量子电子学报， 2013, 30(2): 236-342.

YIN Xin, WANG Hailong, GONG Qian, et al. Binding energy of hydrogenic donor impurity in GaInAsP/InP stepped quantum well[J]. Chinese Journal of Quantum Electronics, 2013, 30(2): 236-342.

[7]郑冬梅，王宗篪，苏春燕．内建电场和杂质对双电子柱形量子点系统束缚能的影响[J]．量子电子学报，2011,28(1):96-103.

ZHENG Dongmei, WANG Zongchi, SU Chunyan. Effect of built-in electric field and impurity on binding energy of cylindrical quantum dot with two electrons[J]. Chinese Journal of Quantum Electronics, 2011, 28(1): 96-103.

[8]丁朝华，苏莉，何锐．磁场对量子线中束缚极化子激发态性质的影响[J]．量子电子学报，2011, 28(6): 748-752.

DING Zhaohua, SU Li, HE Rui. Influence of magnetic field on properties of excited state of bound polaron in quantum wires[J]. Chinese Journal of Quantum Electronics, 2011, 28(6): 748-752.

[9]MAES J, HAYNE M. Electron wave-function spillover in self-assembled InAs∕InP quantum wires[J]. Phys Rev B, 2004, 70(11): 155311(7).

[10]SIDOR Y, PARTOENS B, PEETERS F M. Exciton in a quantum wire in the presence of parallel and perpendicular magnetic fields[J]. Phys Rev B, 2005,71(16): 165323(9).

(责任编辑：孟素兰)