Th（NO3）4-UO2（NO3）2-HNO3-H2O/30%TBP-正十二烷萃取体系主要组分分配比模型

Th(NO3)4-UO2(NO3)2-HNO3-H2O/30%TBP-正十二烷萃取体系主要组分分配比模型

于婷1,2，李峥1,2，赵皓贵1,2，何淑华1,2，何辉3，李晴暖1,2，张岚1,2,*

(1.中国科学院 上海应用物理研究所 放射化学与工程技术部，上海201800；

2.中国科学院 核辐射与核能技术重点实验室，上海201800；

3.中国原子能科学研究院 放射化学研究所，北京102413)

摘要：利用文献报道的Th(NO3)4-UO2(NO3)2-HNO3-H2O/30%TBP-正十二烷体系各组分的分配比实验数据对现有的分配比模型进行分析和比对，提出了一个计算该体系各组分分配比的新模型。利用34组实验数据对新模型进行了验证，符合情况良好。计算结果表明，本文提出的模型明显优于原模型，可作为Th(NO3)4-UO2(NO3)2-HNO3-H2O/30%TBP-正十二烷萃取体系中Th(Ⅳ)、U(Ⅵ)和HNO3萃取行为计算机模拟的基础。模型建立的条件为：温度，25 ℃；U(Ⅵ)浓度，0～100 g/L；Th(Ⅳ)浓度，0～232 g/L；硝酸浓度，0～4.5 mol/L。

关键词：钍；铀；硝酸；分配比；数学模型

中图分类号：TL249 文献标志码：A

收稿日期：2014-07-01;修回日期：2014-08-29

基金项目：中国科学院战略性先导科技专项资助项目(XDA02030000)

作者简介：于婷(1986—)，女，山东淄博人，助理研究员，硕士，核燃料循环与材料专业

doi：10.7538/yzk.2015.49.11.1939

*通信作者：张岚，E-mail: zhanglan@sinap.ac.cn

Distribution Coefficient Model of Main Component in Th(NO3)4-

UO2(NO3)2-HNO3-H2O/30%TBP-dodecane Extraction System

YU Ting1,2, LI Zheng1,2, ZHAO Hao-gui1,2, HE Shu-hua1,2,

HE Hui3, LI Qing-nuan1,2, ZHANG Lan1,2,*

(1.DepartmentofRadiochemistryandEngineering,ShanghaiInstituteofAppliedPhysics,

ChineseAcademyofSciences,Shanghai201800,China;

2.KeyLaboratoryofNuclearRadiationandNuclearEnergyTechnology,

ChineseAcademyofSciences,Shanghai201800,China;

3.DepartmentofRadiochemistry,ChinaInstituteofAtomicEnergy,Beijing102413,China)

Abstract:Based on distribution coefficient data of thorium (Th), uranium (U) and nitric acid in the tributyl phosphate (TBP) extraction system, and by comparing and analyzing the presented distribution coefficient models in the literature, a new mathematical distribution coefficient model with relative computer program for simulating the extraction behavior of Th(Ⅳ), U(Ⅵ) and HNO3 in the TBP extraction system. The reliability of the new model with computer program was verified by 34 sets of distribution coefficient data. The calculated results agree well with the experimental data. The results by comparing the actual distribution coefficient data with the computing results indicate that the calculated results by using this new model are more reliable and accurate than those of SEPHIS model reported previously. The model presented in this work can be a foundation for simulating the extraction behavior of thorium, uranium and nitric acid in the extraction system of Th(NO3)4-UO2(NO3)2-HNO3-H2O/30%TBP-dodecane with uranium concentrations from 0 g/L to 100 g/L, thorium from 0 g/L to 232 g/L, and HNO3 from 0 g/L to 4.5 mol/L at 25 ℃.

Key words：thorium; uranium; HNO3; distribution coefficient; simulation model

我国储量较为丰富的232Th是一种次级核燃料，它可俘获中子生成易裂变物质233U，生成的233U参与裂变称为钍铀燃料循环[1-3]。目前对钍铀燃料元件的后处理均采用Thorex流程，目的是分离回收233U和232Th，钍铀燃料循环工艺尚不成熟，尚未建立工业体系，是当前发展钍铀循环的难点之一[4]。

长期以来，后处理萃取流程研究是通过大量的工艺实验来确定的，因工艺实验要考察的工艺参数较多，需要大量实验才能确定，因此成本昂贵且费时。国内外已开展针对铀钚循环的Purex流程的计算机模拟研究，这种基于萃取流程的数学模拟研究是进行后处理工艺研究的便利工具，不仅可计算各液流的出口浓度，还可透视萃取设备中的动态过程，是后处理流程设计、优化和安全分析的有效工具，而针对钍铀循环的Thorex流程计算机模拟研究鲜见报道[5-8]，因此有必要对此展开进一步研究。分配比模型是后处理Thorex流程计算机模拟研究的基础[9]。尽管之前美国橡树岭国家实验室的Groenier[10]以Richardson[11]分配比理论为基础，使用最小二乘法将Th(Ⅳ)和U(Ⅵ)的分配比拟合成平衡水相总离子强度的函数，分别得到Th(Ⅳ)、U(Ⅵ)和HNO3的多项式函数形式分配比模型。德国Nakashima[12]仍以Richarson分配比理论为基础，将Th(Ⅳ)、U(Ⅵ)和HNO3拟合成为平衡水相中总离子强度的函数，与Groenier提出的SEPHIS模型的Th(Ⅳ)和U(Ⅵ)表观平衡常数计算公式形式上有所差别。德国Germain[13]指出，在30%TBP-煤油体系中,价态相同的元素分配比存在相似性，价态不同，分配比不存在规律性，与Nakashima等的分配比模型和研究结果不谋而合。2013年本研究小组使用62组文献[12]数据和34组实验数据对SEPHIS模型进行验证计算，发现SEPHIS分配比模型对U(Ⅵ)、Th(Ⅳ)和HNO3分配比标准偏差可达100%，90%和70%，尤其是在Th(Ⅳ)平衡水相浓度低于5 g/L时，偏差更为明显。杨金峰等[14]对同一体系各组分的分配比模型等也进行了研究，使用离子强度拟合得到相应的分配比计算公式，模型计算公式与Nakashima的类似，但误差较大，这些模型离准确模拟Thorex流程工艺还存在一定的距离。

因此，为进行Thorex流程相应工艺段的计算机模拟研究，以便进行工艺寻优和安全分析等研究，本文拟在文献[12]数据的基础上开展30%TBP-正十二烷体系Th(Ⅳ)和U(Ⅵ)分配比模型研究，以期得到可用于流程模拟的可靠分配比模型。需要说明的是，虽然文献报道数据实验体系为30%TBP-煤油，本研究拟采用的实验体系为30%TBP-正十二烷，稀释剂有所不同，但文献[2]认为，萃取体系稀释剂只要大部分是由12个碳原子的饱和(链烷烃或环烷烃)碳氢化合物组成，则稀释剂对分配比影响不大。后处理工厂现普遍采用合成煤油作为稀释剂，平均含12个碳原子，大部分为正十二烷，因此本文认为在分配比计算中二者无区别。

1分配比模型及计算结果

1.1分配比模型

Th(NO3)4-UO2(NO3)2-HNO3-H2O/30%TBP-正十二烷萃取体系中，Th(Ⅳ)、U(Ⅵ)、HNO3等组分的萃取机理分别为：

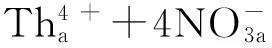
(1)

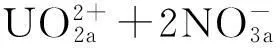
(2)

(3)

各组分形成的络合物被萃取入有机相中，其分配比可通过式(4)～(6)计算，即采用表观平衡常数进行计算：

(4)

(5)

(6)

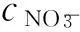
1.2计算结果

公开发表的Th(NO3)4-UO2(NO3)2-HNO3-H2O/30%TBP-正十二烷体系相关组分的分配比模型中以Groenier模型最为成熟，并已投入工艺模拟计算，德国Nakashima所提出的模型是对Th(NO3)4-HNO3共存体系和Th(NO3)4-UO2(NO3)2-HNO3共存体系的，两种体系的计算参数不同，后者不适用于计算极端情况，即U(Ⅵ)含量为0时的分配比。在实际的Thorex流程中，处理的水相是大量钍中含有微量铀，Nakashima模型还是有一定的局限性。

因此，本研究在文献[12]的30%TBP-煤油体系中Th(Ⅳ)和U(Ⅵ)分配比模型(SEPHIS)[10]的基础上使用VB6.0语言编写了计算程序，以文献的数据条件作为程序初始条件，首先计算了62组不同硝酸、铀及钍浓度时，U(Ⅵ)、Th(Ⅳ)和HNO3的分配比。文献中浓度涵盖范围为：平衡水相U(Ⅵ)，0.002 491～13.47 g/L；Th(Ⅳ)，0.134 6～79.81 g/L；HNO3，0.099 6～0.62 mol/L。

文献中的U(Ⅵ)、Th(Ⅳ)和HNO3的分配比的实测值DU.E、DTh.E和DH.E与SEPHIS模型的计算值DU.C、DTh.C和DH.C的对比如图1所示。图中直线斜率为1，实心圆点为同等初始条件的分配比计算值，点越集中于直线上，表明计算值与真实值符合程度越好。从图中可清楚地看到，SEPHIS模型中U(Ⅵ)和HNO3的分配比的偏差较大。

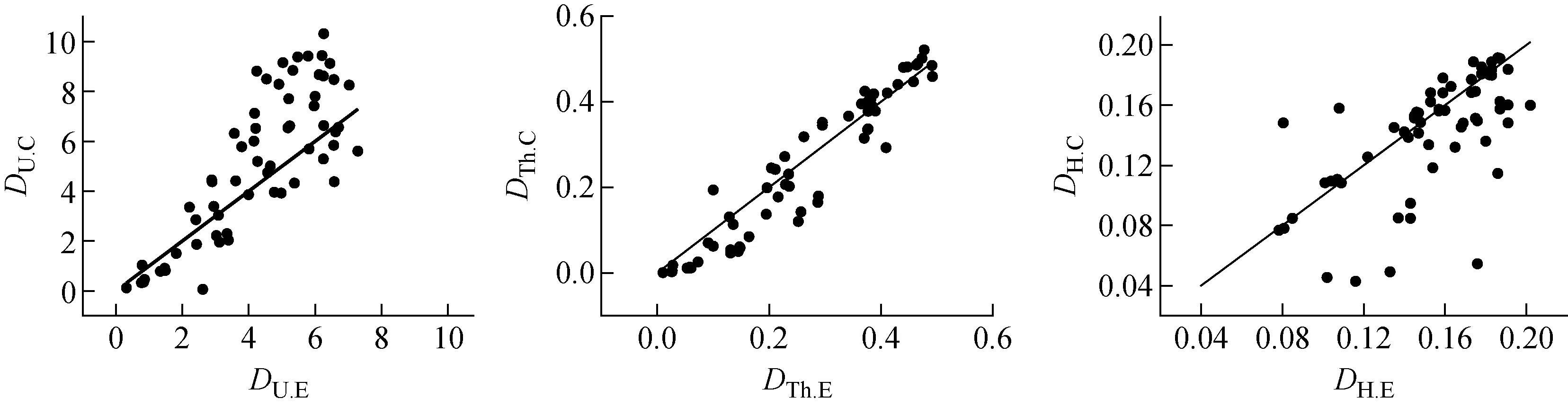
图1　SEPHIS模型各组分的分配比计算值与实测值对比 Fig.1　Comparison of D M.C and D M.E in SEPHIS model

数据来源|REDU|分布<10%10%～20%20%～30%>30%|RE|文献[12]88103638.54数据来源|REDTh|分布<10%10%～20%20%～30%>30%|RE|文献[12]231152330.90数据来源|REDH|分布<10%10%～20%20%～30%>30%|RE|文献[12]381041014.55

2模型改进

基于1.2节分析结果，SEPHIS模型的表观平衡常数的计算以离子强度为基础，所得到的分配比模型的计算结果与实际测量值符合度一般。对模型进一步数据分析，发现在平衡水相总离子强度>2.5 mol/L时，模型计算表观平衡常数与离子强度并不呈一定的函数关系，而是发散状态，可能存在其他影响因素，文献[12]也提及此问题，但仅考虑平衡水相离子强度<2 mol/L范围的计算，因此使用离子强度作为模型的主要参数对计算准确度不构成太大的影响。但若基于对未来Thorex流程准确模拟以及工艺优化的考虑，有必要对模型适用范围进一步扩大，这意味着需考虑总离子强度>2.5 mol/L的情况。以萃取分配比的定义式为研究基础[15]：

(7)

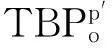
图2　表观平衡常数与平衡水相总NO - 3浓度的关系 Fig.2　Apparent equilibrium constant vs total concentration of NO - 3 in aqueous solution

(8)

则所得各组分的表观平衡常数的计算公式分别为：

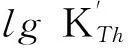
R=0.919 08

(9)

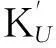
R=0.910 62

(10)

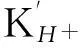
R=0.846 43

(11)

分配比的计算公式为：

(12)

(13)

(14)

(15)

式中，c0,TBP为TBP的初始摩尔浓度。将分配比的计算公式(12)～(14)代入式(15)可得到以下公式：

(16)

3改进后模型与原模型计算结果比对

由图3可看出，从实验的初始条件出发，新模型的分配比计算结果DTh.C、DU.C和DH.C集中在斜率为1的直线上，较SEPHIS模型更接近于实验值。

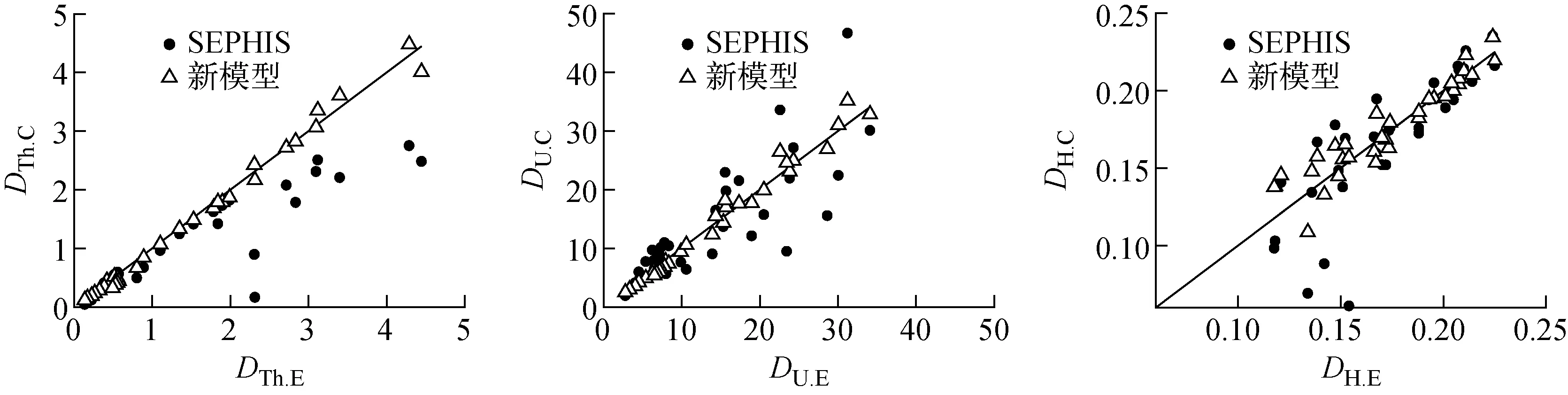
图3　新旧模型各组分分配比计算值与实测值的对比 Fig.3　Comparison of D M.C and D M.E in SEPHIS model and new model

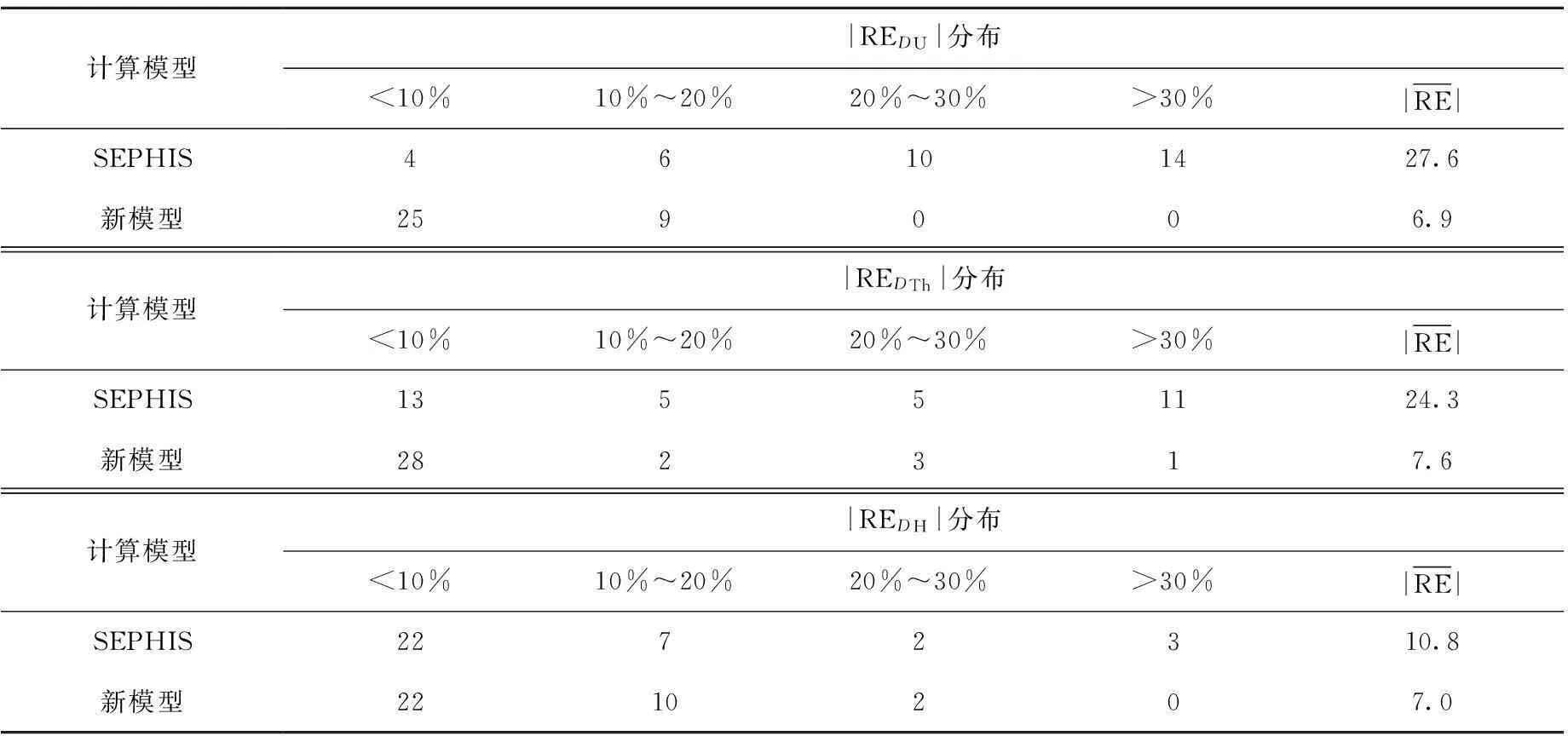
计算模型|REDU|分布<10%10%～20%20%～30%>30%|RE|SEPHIS46101427.6新模型259006.9计算模型|REDTh|分布<10%10%～20%20%～30%>30%|RE|SEPHIS13551124.3新模型282317.6计算模型|REDH|分布<10%10%～20%20%～30%>30%|RE|SEPHIS2272310.8新模型2210207.0

4结论

本文完成过程中得到美国西北太平洋国家实验室夏源贤研究员的指导和帮助，谨致诚挚谢意。

参考文献：

[1]CROSSLAND I. Nuclear fuel cycle science and engineering[M]. US: Woodhead Publishing Ltd., 2012.

[2]本尼迪克特M,皮格福特T H,利瓦伊H W. 核化学工程[M]. 汪德熙，译. 北京：原子能出版社，1988.

[3]江绵恒，徐洪杰，戴志敏. 未来先进裂变核能——TMSR核能系统[J]. 中国科学院院刊，2012,21(3):366-374.

JIANG Mianheng, XU Hongjie, DAI Zhimin. Advanced fission energy program—TMSR nuclear energy system[J]. Bulletin of the Chinese Academy of Sciences, 2012, 21(3): 366-374(in Chinese).

[4]顾忠茂,柴之芳. 关于我国核燃料后处理/再循环的一些思考[J]. 化学进展,2011,23(7):1 263-1 271.

GU Zhongmao, CHAI Zhifang. Some thinking of nuclear fuel reprocessing/recycling in China[J]. Process in Chemistry, 2011, 23(7): 1 263-1 271(in Chinese).

[5]顾忠茂. 钍资源的核能利用问题探讨[J]. 核科学与工程,2007,27(2):97-105.

GU Zhongmao. Probing the problems thorium utilization as a nuclear energy resource[J]. Journal of Nuclear Science and Engineering, 2007, 27(2): 97-105(in Chinese).

[6]何辉,李高亮,陈辉,等. Purex流程共去污工艺计算机稳态模拟[J]. 原子能科学技术，2008，42(9)：769-784.

HE Hui, LI Gaoliang, CHEN Hui, et al. Computer simulation of co-decontamination process in Purex[J]. Atomic Energy Science and Technology, 2008, 42(9): 769-784(in Chinese).

[7]张春龙. Purex 流程中锝萃取行为的计算机模拟[D]. 北京:中国原子能科学研究院,2009.

[8]TACHIMORI S. EXTRM: A computer code system for analysis of the Purex with mixer settler for reprocessing, JAERI-1331[R]. Japan: AERI, 1994.

[9]WATSON S B. User’s guide to the SEPHIS computer code for calculating the Thorex solvent extraction system, ORNL/CSD/TM-70[R]. US: ORNL, 1979.

[10]GROENIER W S. Technical manual for SEPHIS MOD4 version 2.11, ORNL/TM-11569[R]. US: ORNL, 1991.

[11]RICHARDSON G L. Effect of high solvent irradiation exposures on TBP processing of spent LMFBR fuels, HEDL-TME73-51[R]. US: Hanford Engineering Development Laboratory, 1973.

[12]NAKASHIMA T. Distribution data for the system Th(NO3)4: UO2(NO3)2: HNO3/30%TBP in dodecane[J]. Solvent Extraction and Ion Exchange, 1984, 2(4/5): 635-638.

[13]GERMAIN M. Extraction en milieu nitrique du thorium, du neptunium, du plutonium, par les solutions de phosphate de tributyle charges en uranium[J]. J Inor Nucl Chem, 1970, 32: 245-253.

[14]杨金峰,包伯荣,夏源贤,等. 钍铀核燃料后处理萃取过程的数学模拟及工艺流程的计算机优化[J]. 核化学与放射化学,1992,14(1):37-43.

YANG Jinfeng, BAO Borong, XIA Yuanxian, et al. Mathematical models and optimization of solvent extraction process of Th-U fuel reprocessing[J]. Journal of Nuclear and Radiochemistry, 1992, 14(1): 37-43(in Chinese).

[15]姜圣阶,任凤仪. 核燃料后处理工学[M]. 北京:原子能出版社,1995.