自升式平台地震响应分析方法研究

李 宁 ，杨 伟，李 旭*

(1.上海利策科技股份有限公司，天津 300457；2.海洋石油工程股份有限公司，天津 300452)

自升式平台地震响应分析方法研究

李 宁1，杨 伟2，李 旭2*

(1.上海利策科技股份有限公司，天津 300457；2.海洋石油工程股份有限公司，天津 300452)

介绍了自升式平台地震响应不同分析方法的原理，分析了自升式平台与其他结构地震响应分析的不同点。利用有限元软件ANSYS建立了海洋石油92x自升式平台的有限元模型，并分别采用静力法、反应谱法及时程分析法分析了平台在二类场地、设防烈度为8度时的地震响应。对比不同分析方法，其结果表明：反应谱法较静力分析法更保守，而时程分析法对地震波的选取有很大依赖；在地震作用下平台桩腿的弦杆及斜撑受力集中；桩腿上最大等效应力小于材料的屈服强度，平台总体最大位移为0.6 m，该平台能够抵抗8级烈度的地震作用。该研究可为自升式平台的抗震设计提供参考。

自升式平台；地震响应；谱分析；时程分析

0 引 言

我国渤海处于著名的中国东部强震活动构造带——郯庐断裂带上[1]。随着渤海油田的不断开发，海上采油设施即海洋平台的不断建立，海洋工程的抗震问题受到广泛关注。目前，我国渤海海域的海洋平台以导管架平台为主，但将有越来越多的自升式平台应用到渤海油田开采中。自升式平台由一个船体和若干个起支撑作用的桩腿所组成，可适用于不同土壤条件和较大的水深范围，移动灵活方便。对于导管架平台的地震响应分析已有许多学者进行过研究[2-4]，但对于自升式平台，由于其结构形式与导管架平台迥异，因此分析其地震响应的资料尚不多。

目前在我国尚没有专业的海洋平台抗震技术规范，海洋平台抗震设计主要依靠美国石油协会(API)制订的RP2A-WSD规范。因此，结合我国的实际地震情况对海洋平台结构进行地震响应分析是十分必要的。本文采用静力法、反应谱法和时程分析法对自升式平台的地震响应展开分析，比较了不同方法的分析结果，可为自升式平台的抗震设计提供参考。

1 地震分析方法

对于结构在地震下的响应，分析方法主要分为两类：静力法和动力法。下面分别加以介绍。

1.1 静力法

静力法即将结构理想化为不变形的刚体，则地震力为

(1)

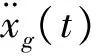
随着对地震研究的深入，人们对该方法不断改进，引入了一些修正系数以使该方法能更好地反映结构的动力特性。我国《海上固定平台入级与建造规范》中给出的便是这种计算方法[6-7]。

平台的地震载荷主要分为地震惯性力和动水压力。

当平台按单点体系计算时，平台甲板处水平向总地震惯性力可按下式计算：

PH=CKHβmg,

(2)

式中：C为综合影响系数，取值0.35～0.5；KH为水平向地震系数；β为相应平台计算方向自振周期为T的动力放大系数；m为位于平台甲板处的质量(包括平台甲板上部结构质量、甲板上的设备质量、75%的备品及供应品质量)以及甲板下部结构质量和其他质量对应平台甲板处的折算质量；g为重力加速度。

当平台按多质点体系计算时，平台质点i对应j振型水平向的地震惯性力Pij应按下式计算：

Pij=CKHγiψijβjmig,

(3)

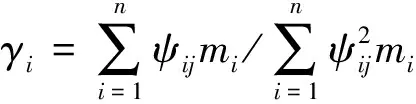
地震时任意向细长构件的水下部分所受动水压力p应按下式计算：

P=CKHβ(CM-1)vγsin2φ(i,j),

(4)

式中：CM为惯性力系数，应尽量由实验确定，在实验资料不足时，对圆形构件可取CM=2.0；v为浸水部分构件体积；γ为流体的容重；φ(i,j)为地震的振动方向i与构件j之间的夹角(rad)；其他参数同上。

1.2 动力法

地震过程是随时间变化的动力过程，采用静力的分析方法不能完全反映结构的动力特性，因此采用动力学的分析方法分析结构的地震响应是必要的。对地震的动力分析方法主要有反应谱法和时程分析法。

1.2.1 反应谱法

反应谱理论是以单质点体系在实际地震作用下的反应为基础，对线性结构进行分析的一种理论。该方法假定：结构物的基础为一刚性盘体；结构处于线弹性阶段；地震时的地面运动可以用地震记录来表示[6,8]。

抗震设计中人们关心的是地震作用的最大值，则对于单点系统，在阻尼比很小的情况下地震持续过程中经受的最大地震作用力为

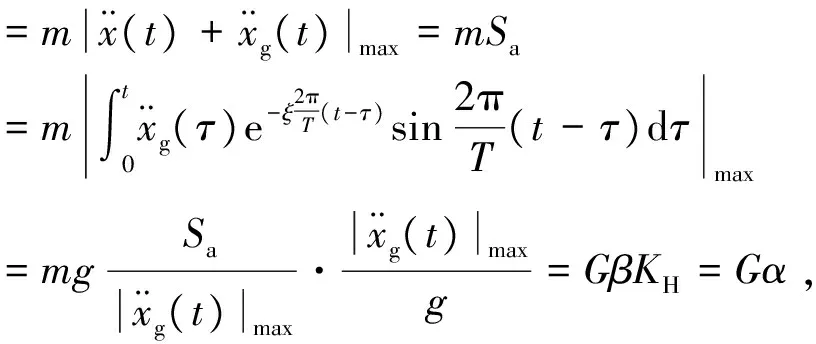
(5)

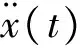
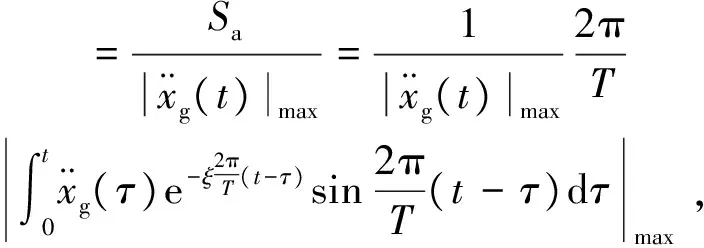
(6)

式中：ξ为结构阻尼比；T为结构周期。

表1 水平向地震系数KH与设计烈度的关系Table 1 Relationship between KH and design intensity

图1 设计反应谱Fig.1 Design response spectrum

对于多自由度体系，一般采用振型分解法计算其所受地震力。对于第j阶振型，沿第i自由度的地震力最大值为

Fij=Giγjφj(i)αj(T),

(7)

有了结构各阶振型的最大地震作用力，则结构总内力反应便可以通过对结构各阶振型下的内力反应进行组合得到。

对于结构响应的振型组合一般有两种计算方法：完全二次组合(CQC)和平方和开平方(SRSS)。对于CQC方法，假定结构总响应为

(8)

对于SRSS方法，结构总响应为

(9)

式中：Skj为j阶振型下的结构响应。

对于平面振动的多质点弹性体系采用SRSS法，对于考虑平-扭耦连的多质点弹性体系采用CQC法。

1.2.2 时程分析

地震作用下结构体系的运动方程可以表示为

(10)

时程分析法是对结构物的运动微分方程直接进行逐步积分求解的方法。这种方法将地震加速度记录数字化，使每一时间对应一个加速度值，根据结构的参数，由初始状态开始按时间推移逐步积分求解运动方程，从而得到结构在整个地震加速度记录过程中随时间变化的位移、速度、加速度，进而可计算出构件内力和变形的时程变化。

由于地震的不确定性，采用时程分析法对大型结构进行抗震设计时，一般应取多条地震波进行分析。目前，国内外进行结构时程分析时所采用的几条实际强震记录主要有适用于I类场地土的滦河波、适用于II类场地土的El-Centro波和Taft波、适用于III类场地土的宁河波[2]。现有的实际强震记录，其峰值加速度多半与建筑物所在场地的基本烈度不相对应，因而不能直接应用，需要按照结构物的设防烈度对波的强度进行全面调整。《海上固定平台入级与建造规范》中规定的地面运动加速度峰值如表2所示。

表2地面运动加速度峰值与设计烈度的关系
Table2Relationshipbetweenpeakgroundaccelerationanddesignintensity

基本烈度789¨xg(t)max/(m·s-2)0．10．20．3

2 地震载荷作用方向及附加水质量

2.1 地震作用方向

地震时地面同时有三个方向的运动，两个水平方向及一个竖直方向，一般竖向最大加速度与水平最大加速度的比值为0.42～0.67。因此单独采用一个方向的地震作用对结构进行分析不能完全反映地震时结构的响应。API-2A中规定地震响应分析时应在两个水平正交方向施加地震作用，并在竖直方向施加1/2的地震作用。

2.2 附加水质量

海洋平台位于水下的结构在振动时都有一定量的水体随之一起运动。海洋平台与陆地结构的不同之一便是存在一定的附加质量[9]。

参考《海上固定平台入级与建造规范》中的规定，对于圆形管件其附加水质量可按下式计算：

m=ρπr2l,

(11)

式中：m为浸入水中结构产生的附加水质量；ρ为水密度；r为管件外半径长度；l为浸水杆件长度。

3 结构响应最大值确定

对于一般的平台，地震时使结构同时受到三个方向的作用，但是这三个方向的作用不能使结构的响应同时达到最大值，因此简单地将各个方向的最大响应通过CQC或SRSS方法确定结构响应的最大值是不合理的。挪威船级社(DNV)规范规定，结构的最大响应按下式确定：

(12)

式中：R1、R2、R3分别为地震作用的三个正交方向上结构响应的最大值。

4 海洋石油92x地震响应分析

海洋石油92x自升式钻井平台为三角形船体，带有三个三角形桁架桩腿，每个桩腿由下端的桩靴支撑。海洋石油92x型长57.2 m，型宽53.34 m，型深7.62 m，正常工作状态下桩腿长度94 m，气隙14.02 m，水深60.96 m，入泥深度4.57 m，如图2所示。

4.1 有限元模型的建立

本文以上述海洋石油92x参数建立有限元分析模型，根据规范规定仅分析地震作用下的结构响应，不与其他工况进行组合。为计算简便，将平台主体简化为一环形梁，将结构恒载及0.75倍的活载荷转化为材料密度均匀分布在环梁上，通过提高水下桩腿的材料密度来考虑附加水质量，桩腿按海底泥面下3 m处铰支来模拟其有限元模型的边界条件[10]。有限元模型如图3和图4所示。

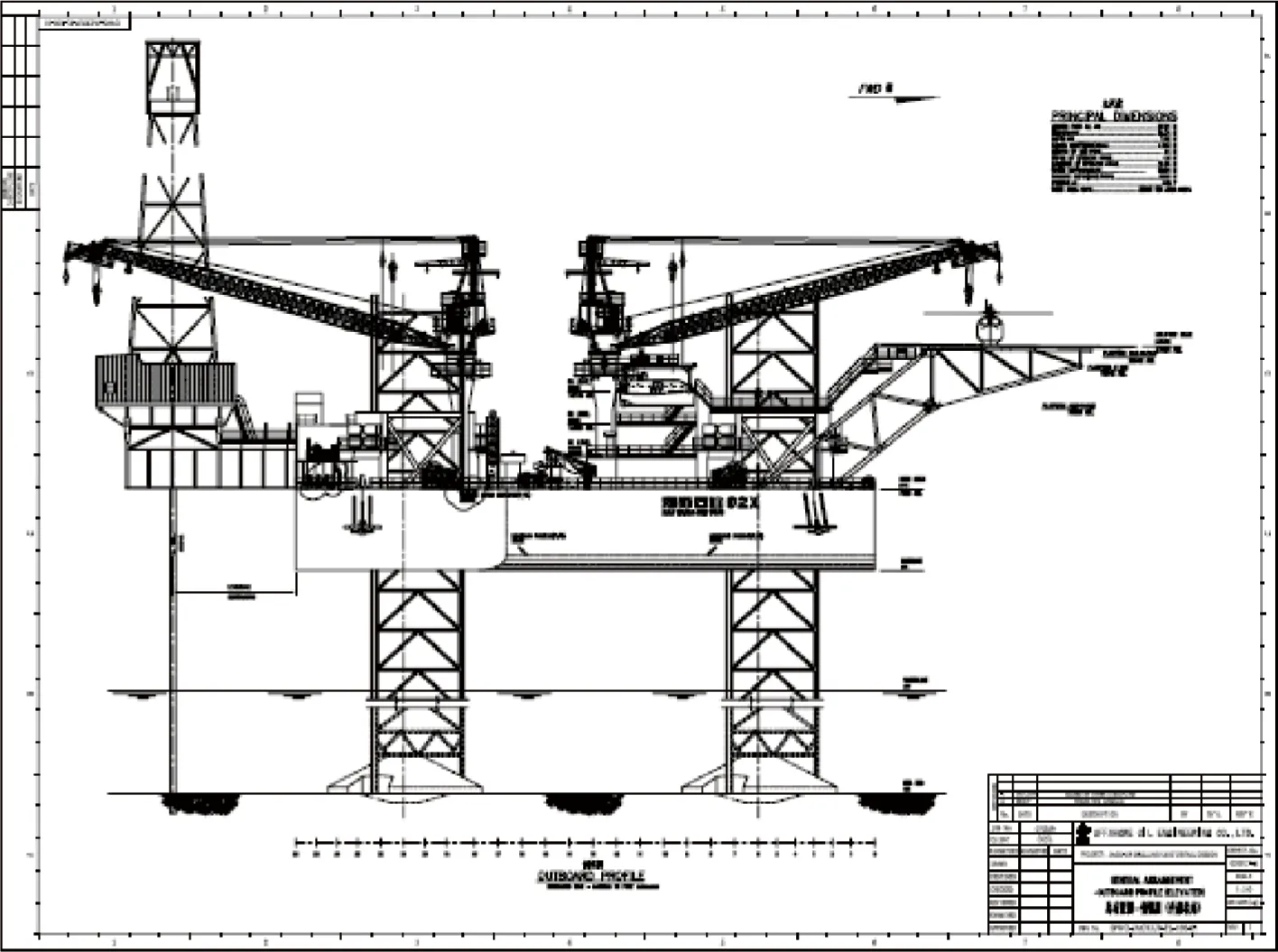
图2 海洋石油92xFig.2 HYSY 92x

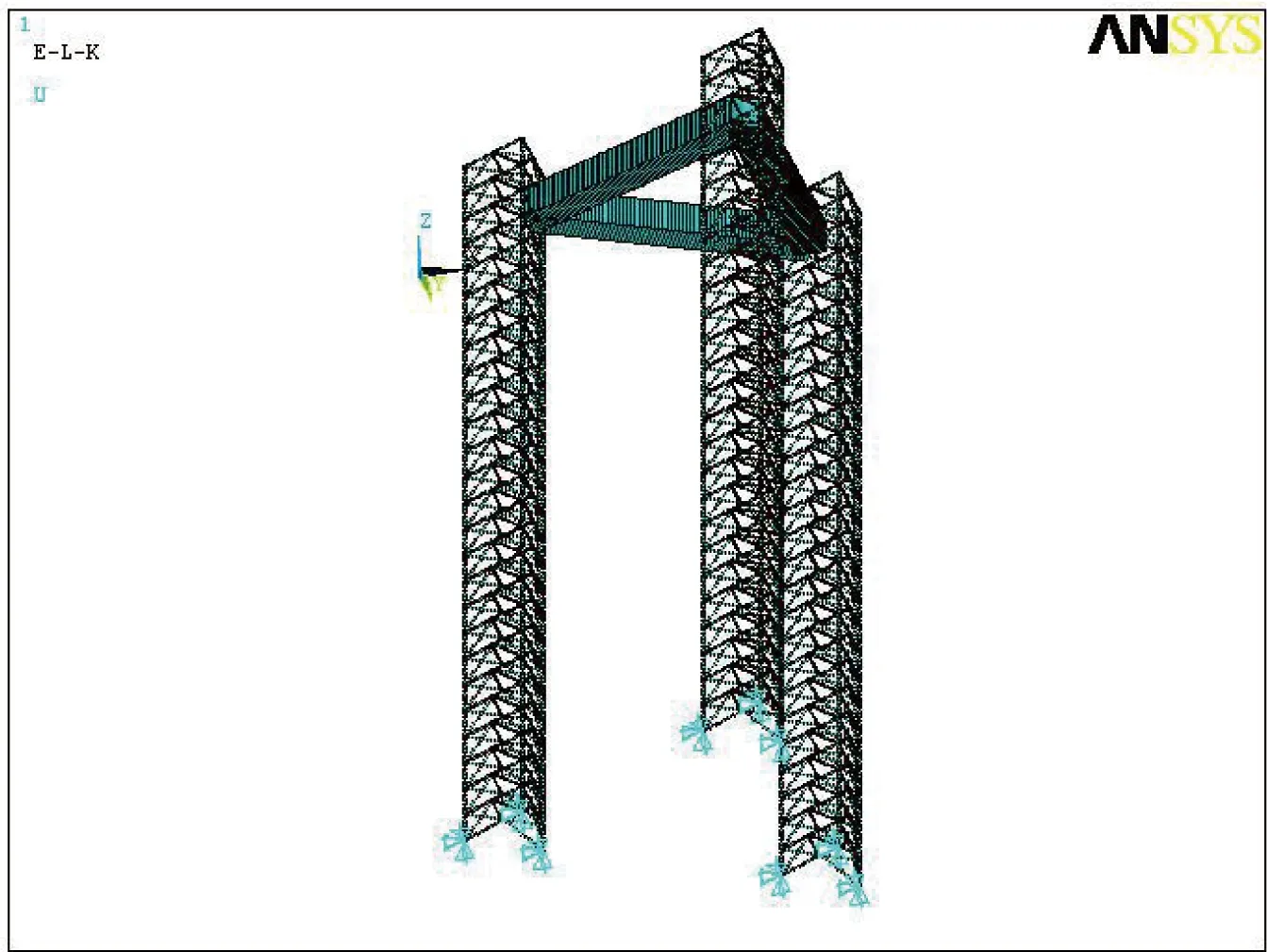
图3 海洋石油92x有限元模型Fig.3 Finite element model of HYSY 92x

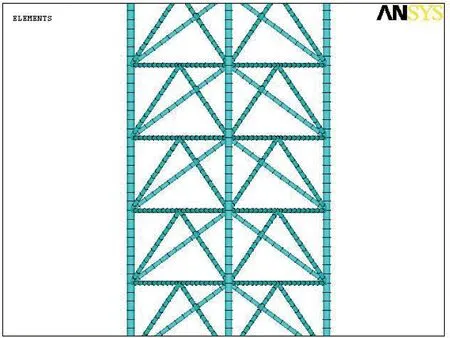
图4 海洋石油92x桩腿细部有限元模型Fig.4 Detailed finite element model of HYSY 92x leg

4.2 静力分析

假定平台处于二类场地，设防烈度为8度。将平台按单质点系统计算水平地震力及动水压力，仅考虑水平地震作用，取综合影响系数C=0.5，则体系地震作用下的总体变形及等效应力如图5和图6所示。

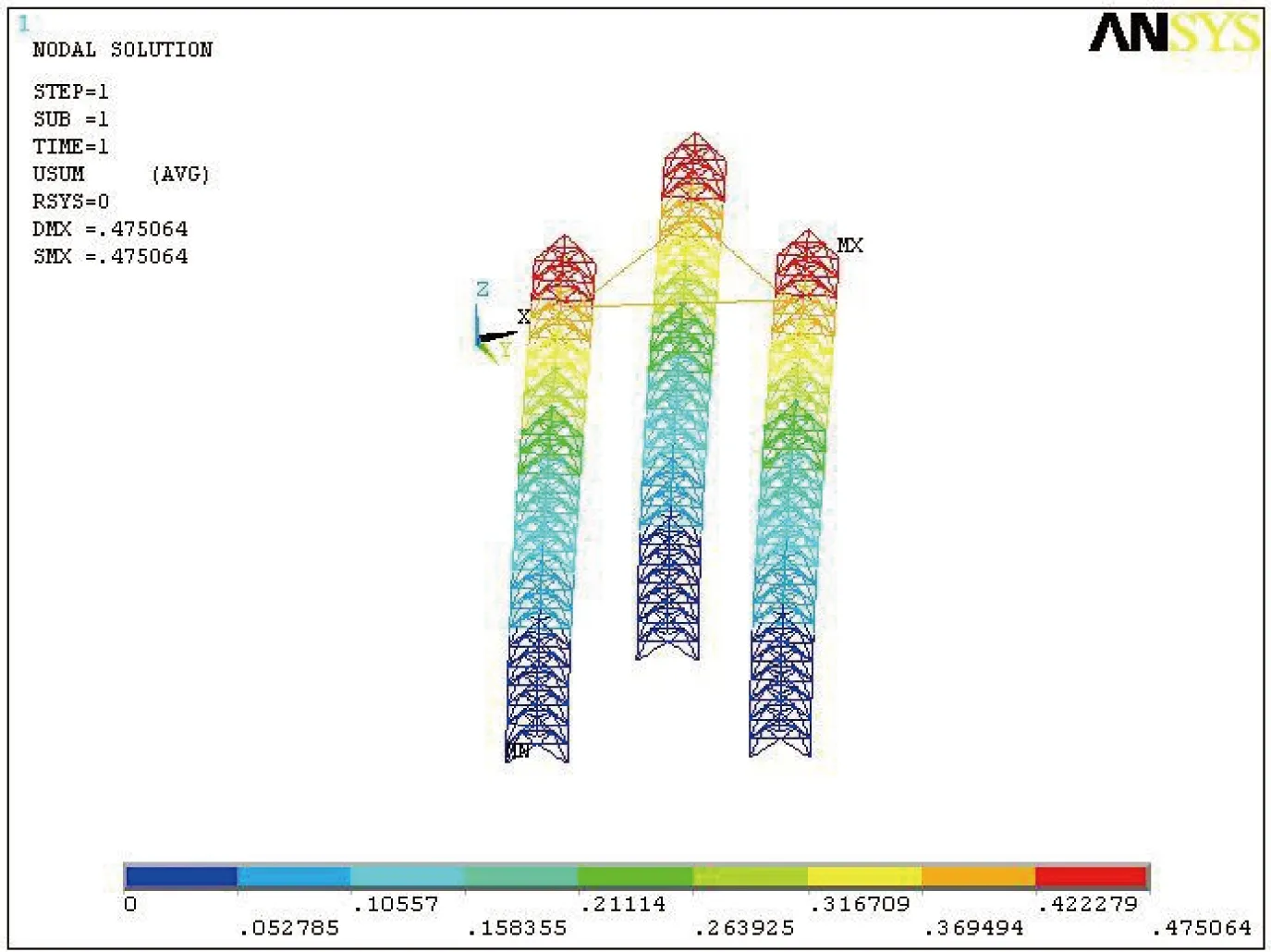
图5 静力计算总体变形Fig.5 General deflection based on static analysis

图6 静力计算总体等效应力Fig.6 Von Mises stress contour based on static analysis

由分析可知，在地震载荷的作用下，结构最大位移发生在桩腿顶端节点处(节点编号4033)，位移值为0.474 4 m；等效应力最大值出现在桩腿根部，其值为182 MPa，这是因为桩腿根部与海底连接，在水平地震力作用下根部的弯矩较大。

4.3 结构自振分析

结构自振频率和周期如表3所示。

4.4 自升式平台反应谱分析

假定各个方向的地震作用相互独立，取结构的前25阶振型进行谱分析，对反应谱曲线进行离散，对于x、y作用方向取表4所示反应谱值进行反应谱分析，对于z作用方向取0.5倍的反应谱值进行分析。则结构处于二类场地，设防烈度为8度时结构在不同方向地震作用下的变形如图7～9所示。

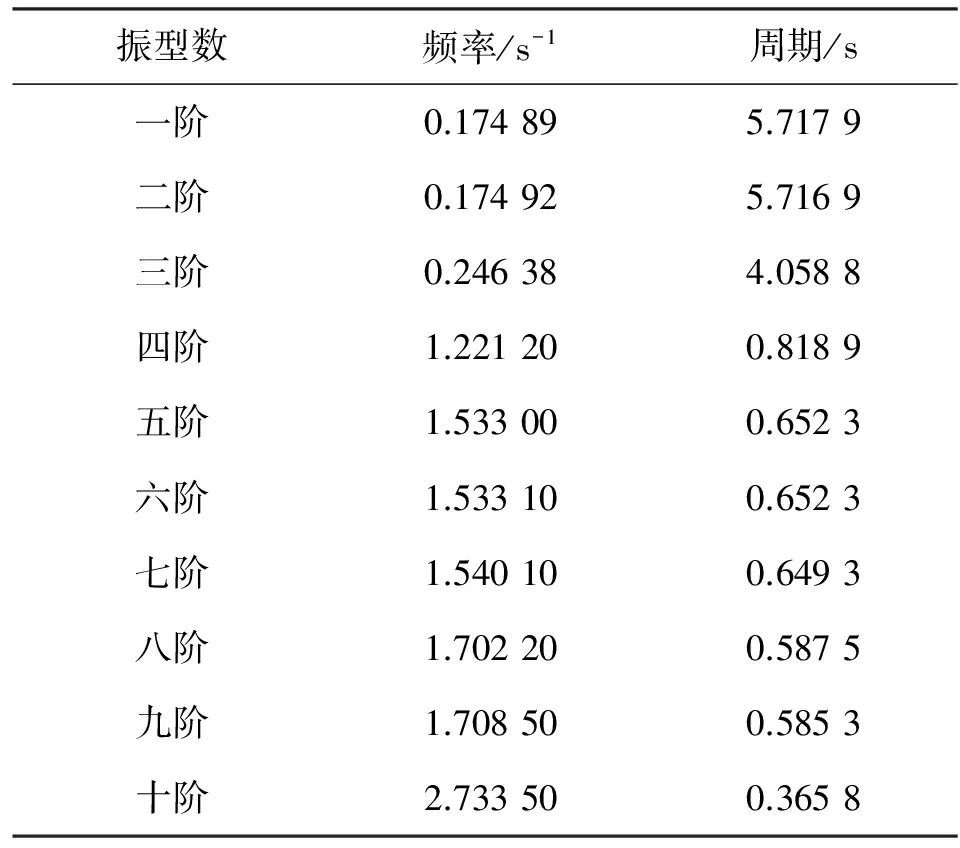
表3 结构自振频率及周期Table 3 Natural frequencies and periods of the structure

表4结构处于二类场地时反应谱值
Table4Responsespectrumvaluesofthestructureatsecondaryground

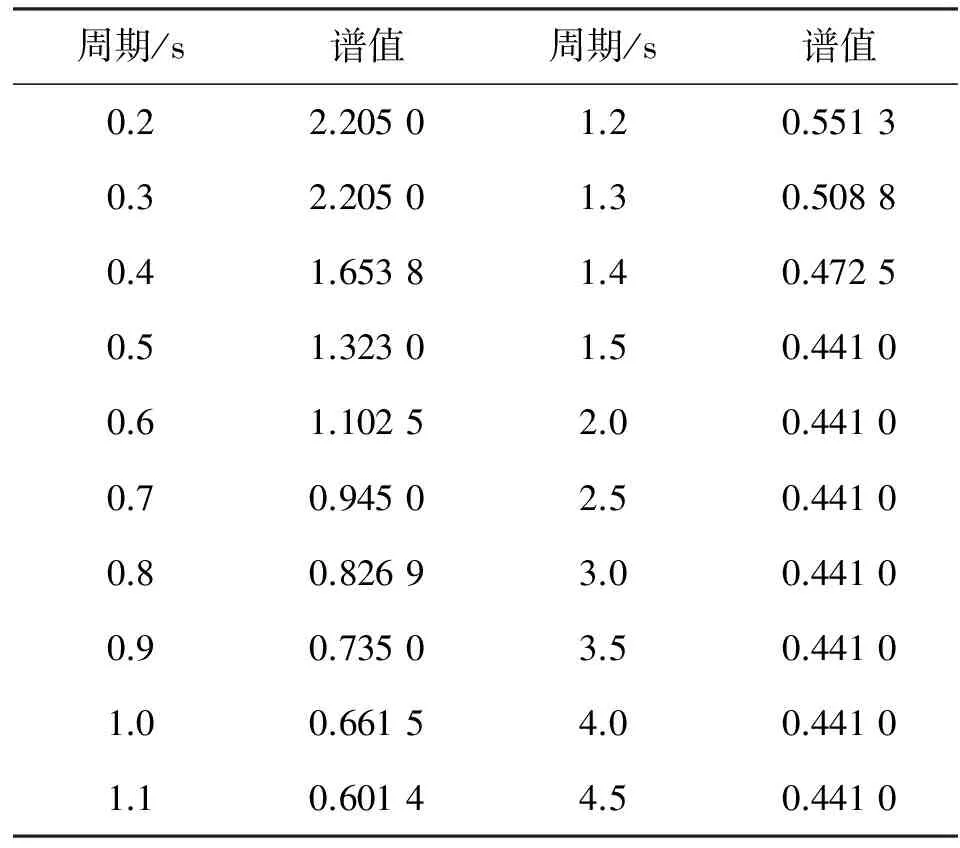
周期/s谱值周期/s谱值0．22．20501．20．55130．32．20501．30．50880．41．65381．40．47250．51．32301．50．44100．61．10252．00．44100．70．94502．50．44100．80．82693．00．44100．90．73503．50．44101．00．66154．00．44101．10．60144．50．4410

图7 x方向谱分析总变形Fig.7 General deflection with spectrum analysis at x direction

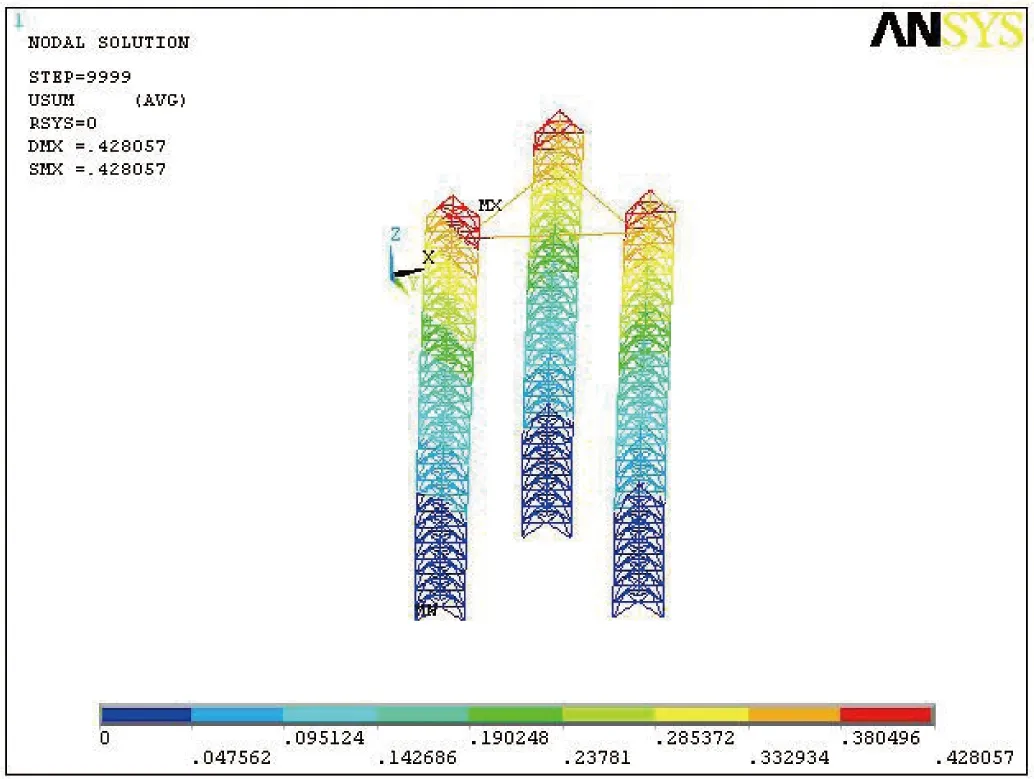
图8 y方向谱分析总变形Fig.8 General deflection with spectrum analysis at y direction

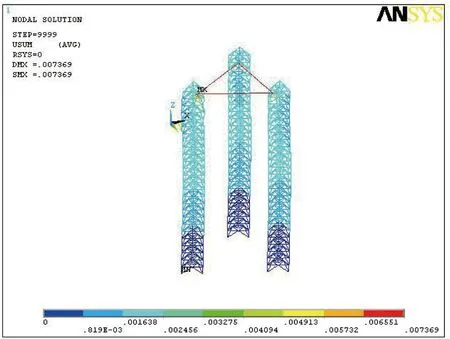
图9 z方向谱分析总变形Fig.9 General deflection with spectrum analysis at z direction

平台桩腿顶端节点(节点编号4033)在不同作用方向时的位移如表5所示。

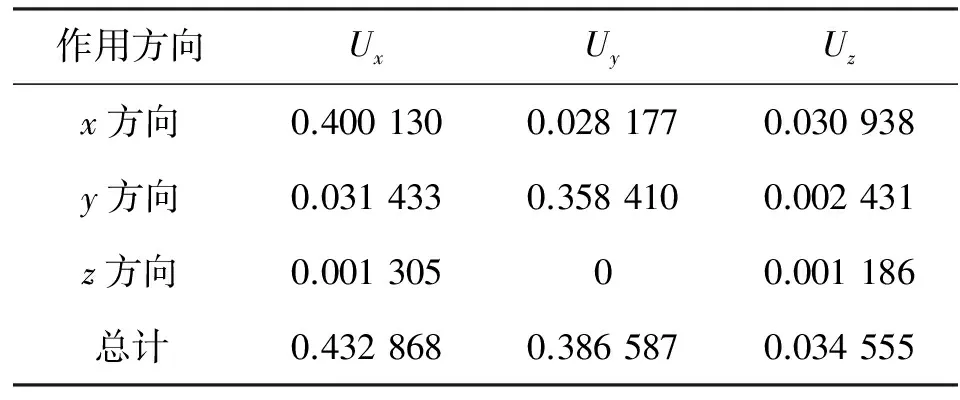
表5 二类场地谱分析桩腿顶端节点(节点编号4033)位移Table 5 Deflections of leg top node (node number 4033) with spectrum analysis at secondary ground m

4.5 时程分析

本文分别采用El-Centro波及Taft波进行分析，并对各地震波记录进行调幅使其峰值加速度为2 m/s2，以满足8度设防的要求。分析过程中地震波作用方向采用x+y+0.5z的形式。

4.5.1 El-Centro波作用下结构地震响应

调幅后El-Centro波的各方向加速度时程曲线如图10所示。

El-Centro波作用下桩腿顶端节点(节点编号4033)位移时程曲线如图11所示。

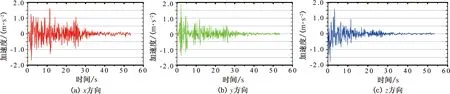
图10 El-Centro波加速度时程曲线Fig.10 El-Centro wave acceleration time histories

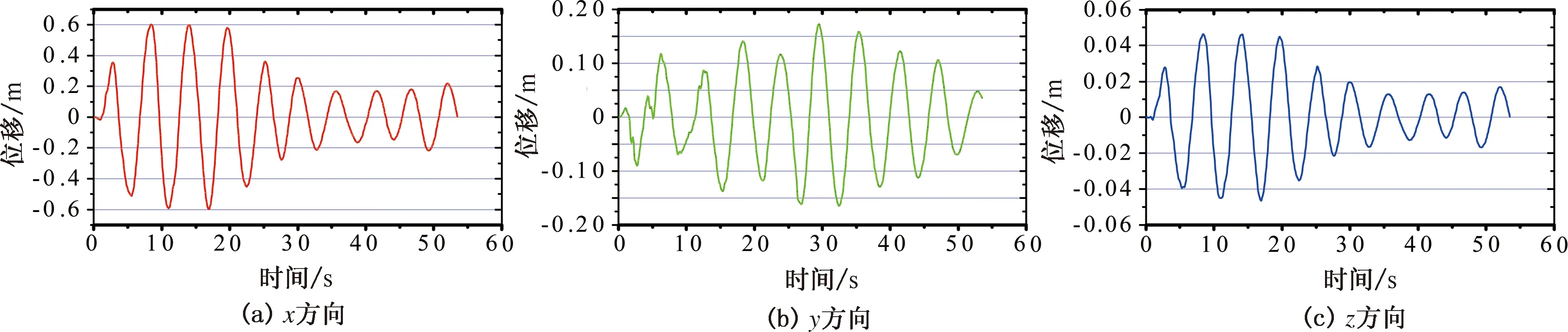
图11 El-Centro波作用下桩腿顶端节点(节点编号4033)位移时程曲线Fig.11 Displacement time histories of leg top node (node number 4033) under El-Centro wave

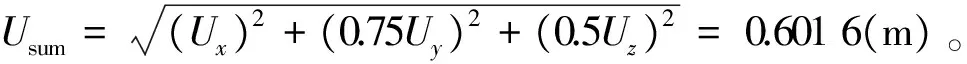
4.5.2 Taft波作用下结构地震响应

调幅后Taft波的各方向加速度时程曲线如图13所示。

Taft波作用下桩腿顶端节点(节点编号4033)位移时程曲线如图14所示。

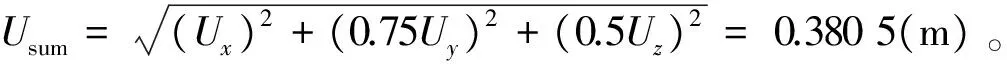
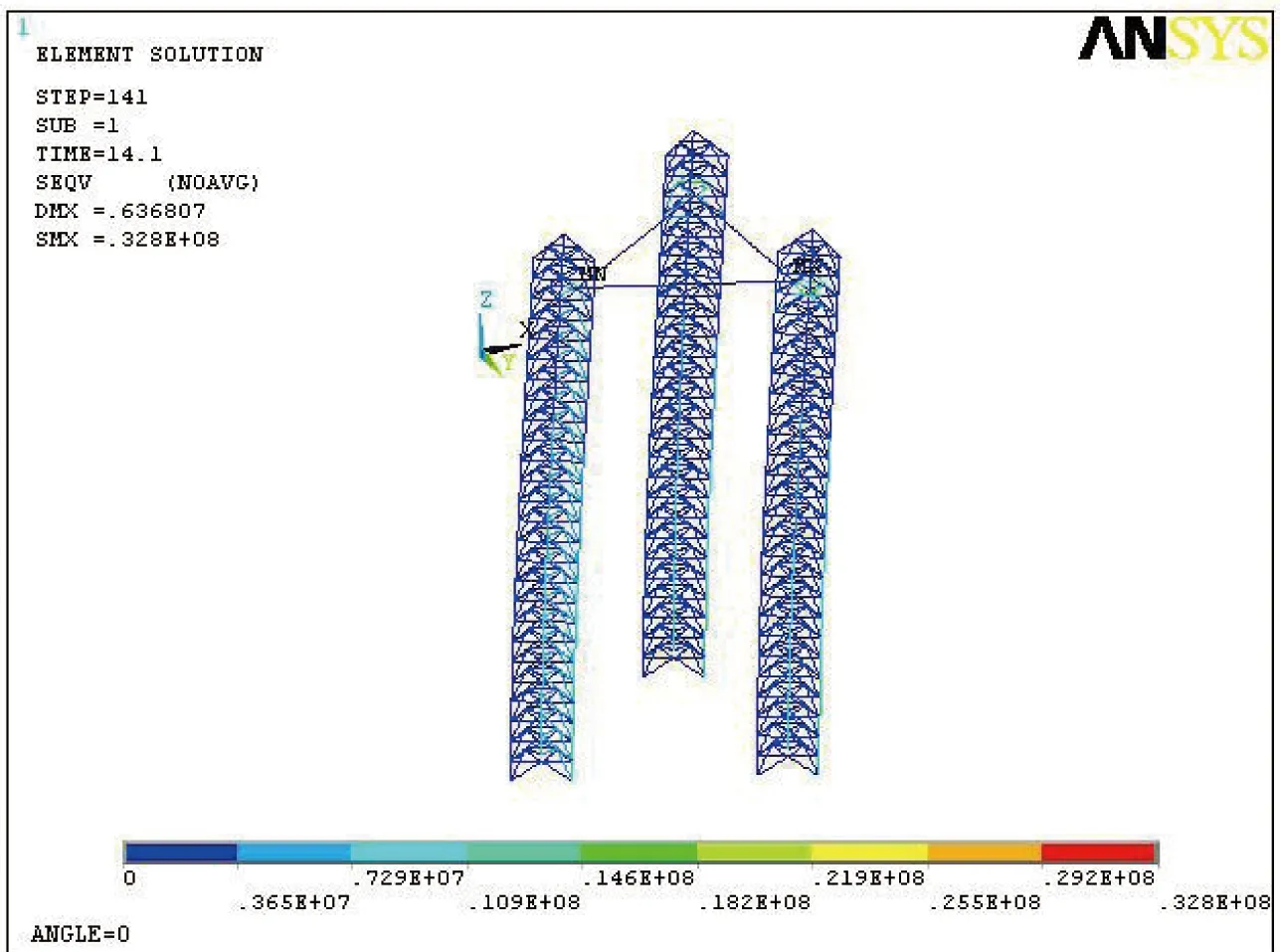
图12 El-Centro波作用下桩腿底部弦管等效应力最大时总体等效应力图Fig.12 General Von Mises stress contour while the equivalent stress in the chord at the bottom of leg reaches the maximun value under El-Centro wave

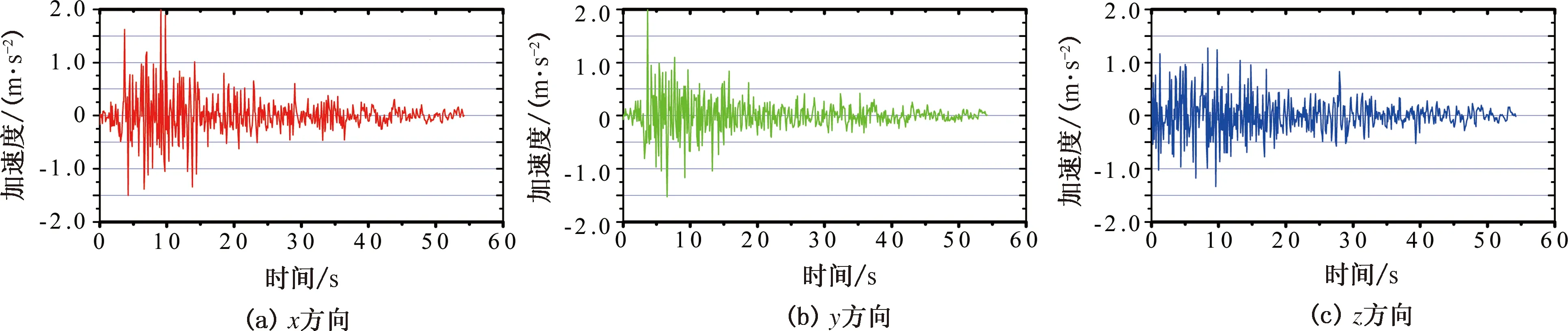
图13 Taft波加速度时程曲线Fig.13 Taft wave acceleration time histories

图14 Taft波作用下桩腿顶端节点(节点编号4033)位移时程曲线Fig.14 Displacement time histories of leg top node (node number 4033) under Taft wave

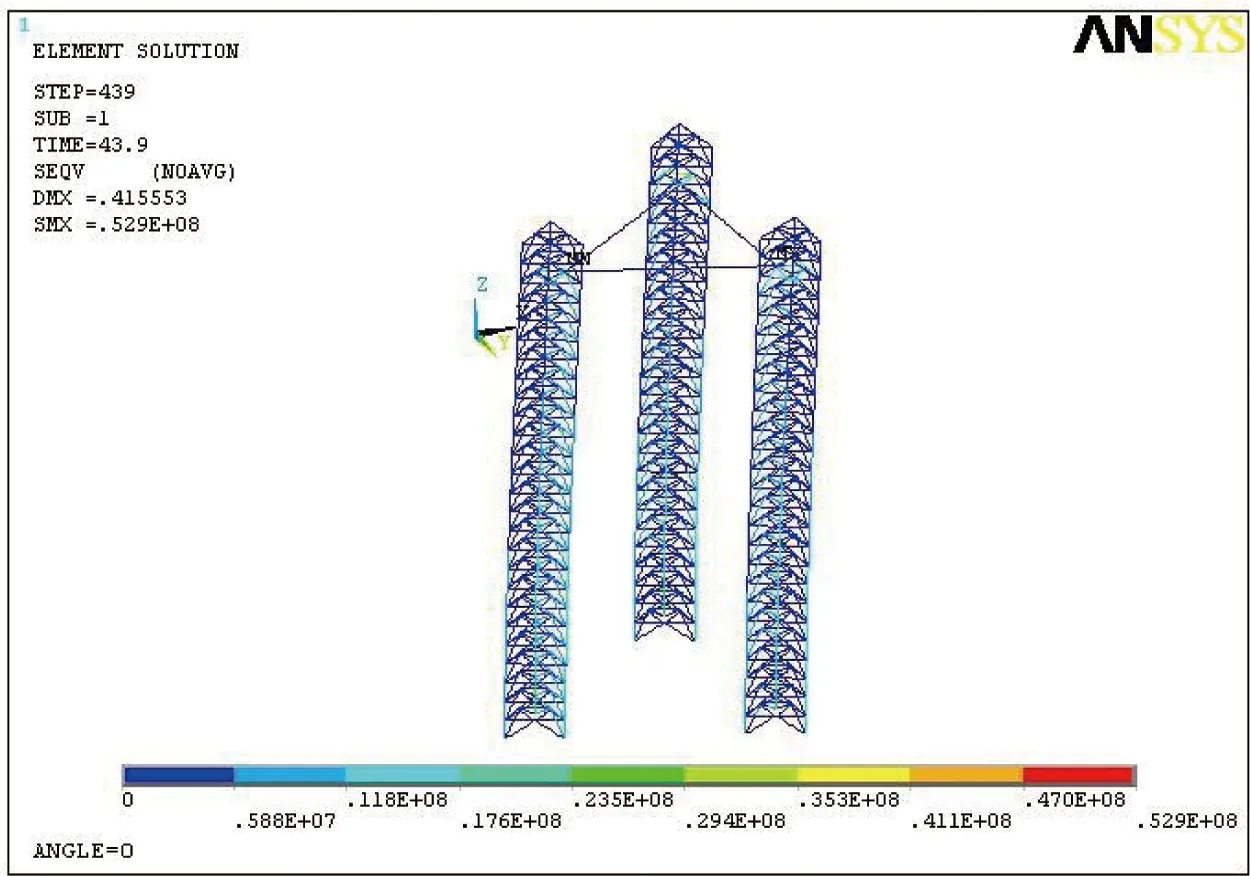
图15 Taft波作用下桩腿底部弦管等效应力最大时总体等效应力图Fig.15 General Von Mises stress contour while the equivalent stress in the chord at the bottom of leg reaches the maximun value under Taft wave

4.6 不同计算方法结果对比

不同计算方法结果对比如表6所示。

表6 不同计算方法结果对比Table 6 Calculation results obtained by different methods

5 结 语

对比不同分析方法下的结构位移及应力响应可知，平台在El-Centro波作用下的响应最大，其桩腿底部等效应力为225 MPa，小于材料的屈服强度690 MPa，桩腿顶端位移最大值为0.601 6 m，在允许范围之内，所以结构能够抵抗8级烈度地震的作用。采用反应谱法分析结构的地震作用与静力法相比要保守一些；对于时程分析方法，结构的地震响应对不同的地震波差别很大，因此地震响应分析时应同时采用反应谱及时程分析方法以确定结构的最不利反应。由时程分析可知，在地震作用下平台桩腿处的弦杆、斜撑受力较大，因此在设计时应对此处构件采用高强度钢并同时合理分配构件间的相对刚度，使结构的应力响应得到合理的分布。

[1] 彭艳菊，吕悦军，唐荣余，等.探讨渤海及周边地区海洋平台抗震设防水准[J].地震学报，2005，27(6)：650.

[2] 韩晓双.导管架海洋平台地震响应研究[D].大连：大连理工大学，2008.

[3] 荣棉水，彭艳菊，吕悦军.导管架式海洋平台的地震动时程分析[J].世界地震工程，2009，25(1)：25.

[4] 魏巍.导管架式海洋平台地震破坏状态分析研究[D].青岛：中国海洋大学，2004.

[5] 王焕定，章梓茂，景瑞.结构力学第2版 [M].北京：高等教育出版社，2004:257-273.

[6] 中国船级社.海上固定平台入级与建造规范[S].1992.

[7] 亓和平.浅海桩腿自升式钻井平台地震响应分析[J].中国海洋平台，2003，18(4):11.

[8] 汪庠宝，韩继文.自升式海上钻井平台结构的模态分析及地震反应的谱分析[J].海洋工程，1988，6(4):1.

[9] 潘斌.移动式平台设计[M].上海：上海交通大学出版社，1995：77-79.

[10] 中国船级社.海上移动平台入级与建造规范[S].2005.

StudyonSeismicResponseAnalysisMethodforJack-UpPlatform

LI Ning1,YANG Wei2,LI Xu2

(1.ShanghaiRichtechEngineeringCo.,Ltd.,Tianjin,300457,China; 2.OffshoreOilEngineeringCo.,Ltd.,Tianjin300452,China)

The different seismic response analysis methods and the differences of the seismic response between the jack-up platform and other structures are introduced.The HYSY 92xjack-up platform model is built with ANSYS software,and the seismic response is analyzed with static method,response spectrum method and time-history analysis method when the secondary ground and the 8 seismic fortification intensity are considered.The analysis shows that:the response spectrum method is more conservative than the static method; the seismic response of the jack-up platform obtained with the time-history analysis method depends on the selection of seismic wave; in the leg,the stress is concentrated in the chords and the sway rods; the maximum Von Mises stress in the chords of the leg is less than the material yield strength,and the maximum displacement is 0.6 m,so the platform can resist the seismic effect.This research can provide reference for the seismic design of the jack-up platforms.

jack-up platform; seismic response; response spectrum method; time-history analysis

2015-11-25

李宁(1983—)，女，硕士，工程师，主要从事海洋工程结构设计研究。

*通信作者

TE53

A

2095-7297(2016)01-0031-08