一种新的分布式卫星凝视成像方法∗
(中国人民解放军63771部队,陕西渭南714000)
0 引言
相比于光学观测方法,主动式微波观测方法具有全天候、全天时的特点,被广泛应用于全球通信、观测等领域。合成孔径雷达(Synthetic Aperture Radar,SAR)[1-3]通过合成孔径技术,利用目标的多普勒频移信息,实现了高精度的目标分辨能力,使得空间对地观测成像成为可能。但是合成孔径雷达成像要求目标与雷达之间必须存在相对运动,这一约束条件导致很难对高速运动目标(合成孔径时间内运动距离超过一个分辨单元)、非合作运动目标进行成像。欧空局、美国的NASA、DAPRA等机构都已将寻找一种不依赖于相对运动的空间观测方法作为未来技术研究的重要方向。
基于量子关联成像发展而来的微波关联成像,是一种全新的成像方式[4-5]。其通过发射二维空间-时间不相关的雷达信号,通过波阵面上各阵点之间的不相关性实现二维分辨能力。空间 时间不相关波形的实现是微波关联成像的难点之一。目前主要的实现方式是通过阵列天线发射单频信号,通过随机白噪声或混沌序列对单频信号进行调制。这种方式所获得的相干系数较低,成像结果各像元间存在相互干扰,而且成像的分辨率受限于阵列天线的个数。新提出的一种通过涡旋天线发射涡旋场实现关联成像的方式,理论上可以通过相位信息解算出目标极坐标系下半径向和角度向信息,但成像方法较为复杂,还处于初步研究阶段。
在合成孔径成像理论和微波关联成像理论的基础上,考虑到相对运动对SAR的约束性,以及二维空间-时间不相关信号的难实现性,本文提出一种不依赖于雷达与目标相对运动的准实时成像方法——基于一维微波关联成像技术的分布式卫星凝视成像方法。第1节介绍了一维微波关联成像的信号模型及一维微波关联成像的原理;第2节介绍了分布式卫星凝视成像的原理,给出了目标位置信息、幅度信息的解算方法;第3节通过稀疏目标仿真试验对所提出的原理与方法的正确性进行了验证[6]。
1 一维微波关联成像
1.1 一维空间-时间不相关信号模型
二维空间-时间不相关信号实现较为复杂,而一维空间-时间不相关信号很容易实现。为实现一维微波关联成像,提出了一种倍频步进频的信号模式,其时频图如图1所示。建立倍频步进频信号模型表达式为
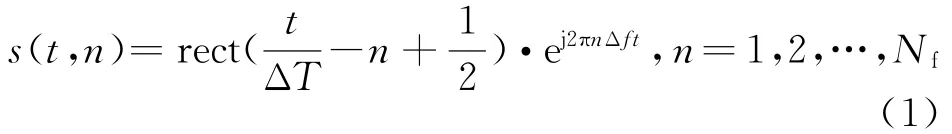
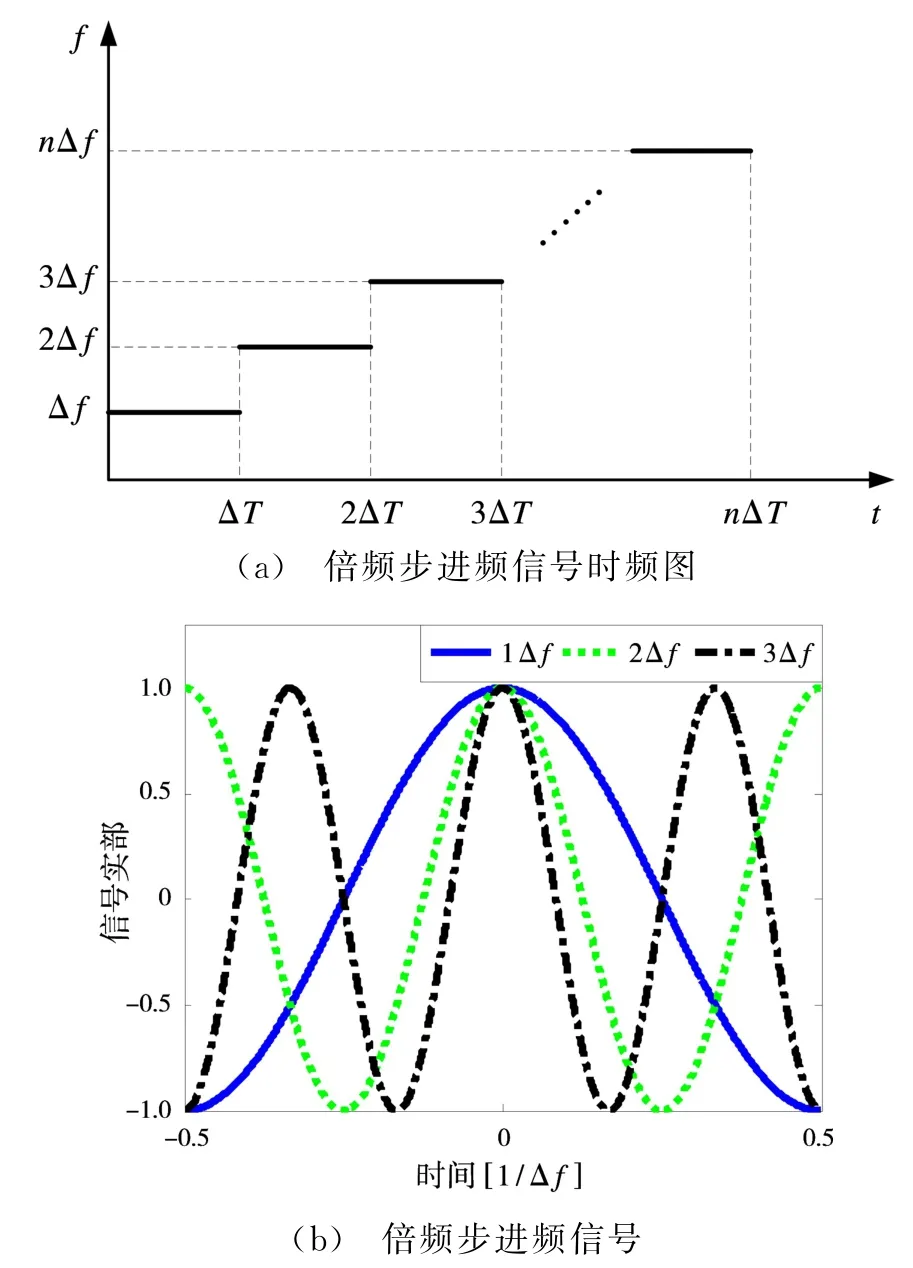
图1 倍频步进频信号模型
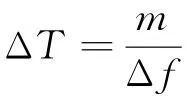
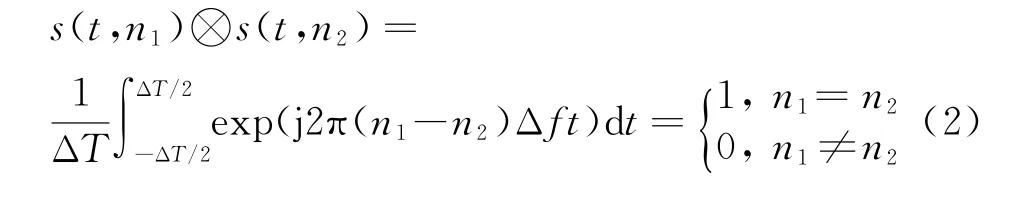
1.2 一维微波关联成像原理
建立一维微波关联成像几何模型,如图2所示。当t0=2R0/c时刻,R0处的信号回波到达接收机,为便于理解,假设回波延迟都是由于发射单程所引起的。如此,每一个频点都会与地面上的一个分辨单元所对应的斜距形成一一映射,其满足下式关系:

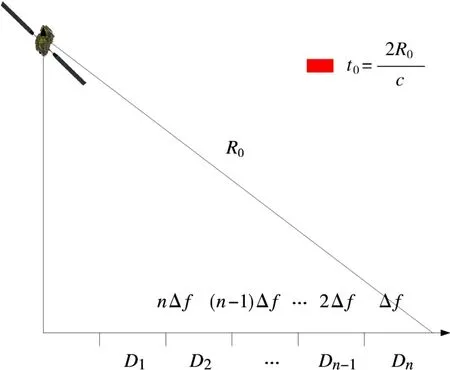
图2 频点与分辨单元对准
式中,等式左边第一项代表了单频的发射延迟,第二项代表了传播延迟,f表示频率,r表示斜距,为区别去正交坐标系,本文称之为距离环。通过式(3)可以得到f与r的对应关系:
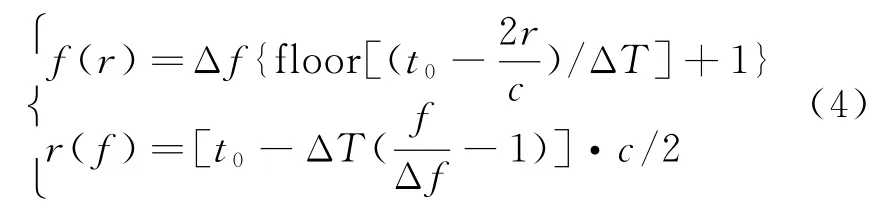
此时,接收机开启,接收一个ΔT内的回波信号。位于距离环r上的目标所对应的回波信号为
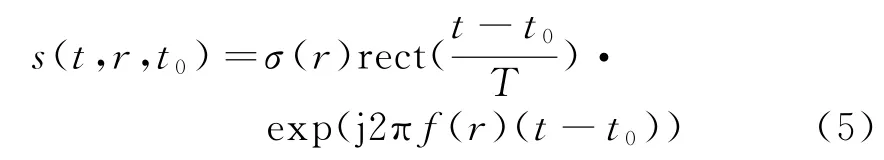
整个测绘带内回波信号为
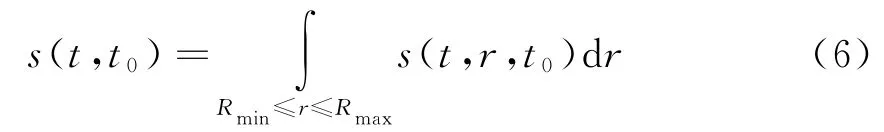
式中,Rmax,Rmin分别代表所有单频所对应的最远、最近的距离环。
然后将s(t,t0)与各单频信号s(t,n)取相关,即可得到半径向的“压缩”结果-距离环:
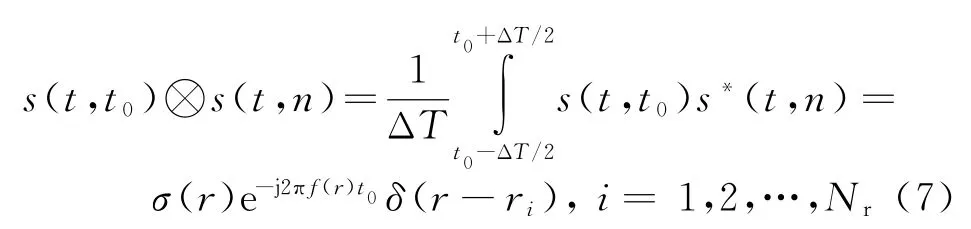
式中,r i=[t0-ΔT(i-1)]·c/2,Nr为距离环的个数。距离环的一维、二维图像如图3所示。
2 分布式卫星凝视成像
2.1 解算目标角度向信息
传统的SAR成像处理是在距离向和方位向实现二维距离分辨能力,而一维微波关联成像只能获得一维距离分辨能力,因此考虑采用极坐标系,通过一维微波关联成像实现极坐标系下半径向的距离分辨。s然后通过N(N>2)颗分布式卫星进一步解算目标的角度向信息,从而确定目标坐标。其原理示意图如4所示。
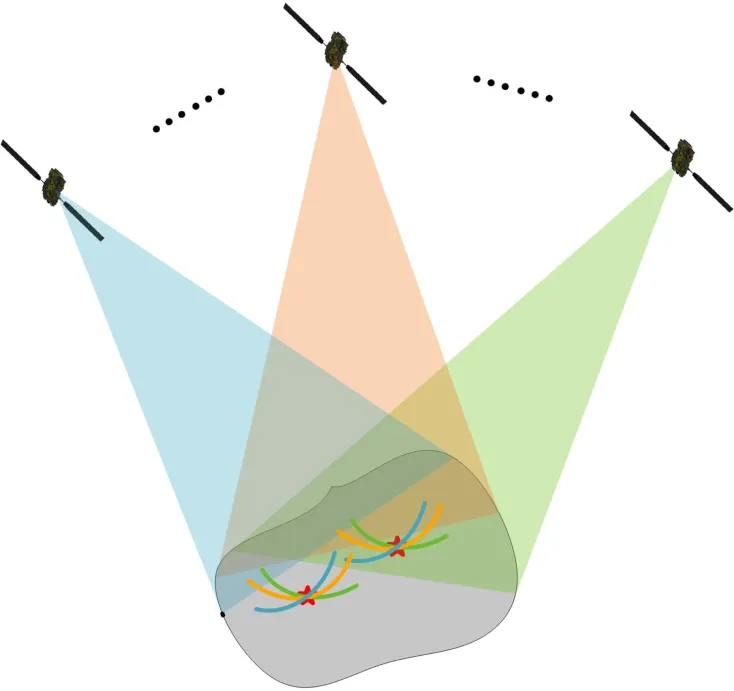
图4 一维微波关联成像原理图

通过遍历场景的每一个像素点,将极坐标系下的距离环都映射到场景中,同时位于N个距离环交点处的像素点即为目标点的坐标,即同时满足N个方程的解。由此即可得到目标场景坐标系下的二维坐标(x,y)。图5给出1个点目标在3部雷达照射下形成的3个距离环图像。
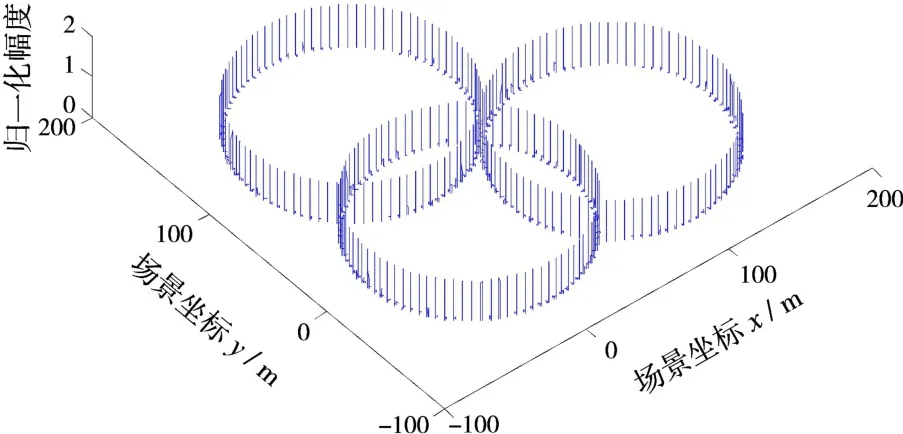
图5 1个目标点3部雷达形成的距离环图像
2.2 解算目标幅度信息
假设每个距离环的幅度等于位于此距离环上所有目标点的幅度之和,即
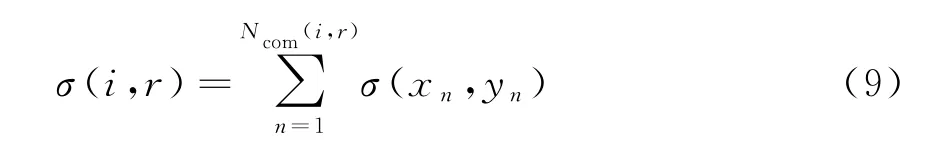
式中,σ(i,r)表示第i部雷达斜距为r的距离环幅度,Ncom(i,r)表示位于此距离环上的点目标的个数,σ(x n,y n)表示场景坐标系下位于(x n,y n)处的目标幅度。
对于每一部雷达,其生成的距离环数满足:

则总的距离环数为
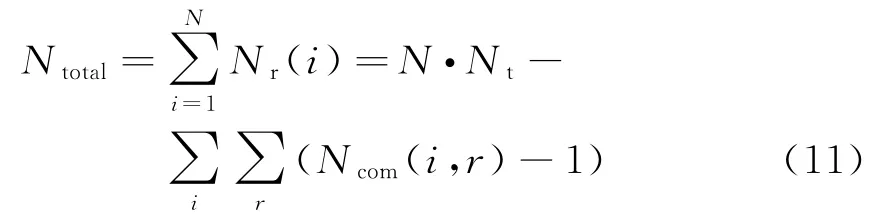
显然,Ntotal>Nt。根据式(9),可建立Ntotal个方程组,而其中的未知数的个数为Nt个。故该方程组可解,所得的解即为各目标的幅度值。
3 仿真校验与分析
为验证基于一维微波关联成像技术的分布式卫星凝视成像方法的有效性,建立了分布式卫星凝视成像系统模型,该系统通过3颗分布式卫星对地面稀疏场景中的5个目标点进行照射成像。系统几何模型如图6所示,卫星及雷达参数如表1所示。
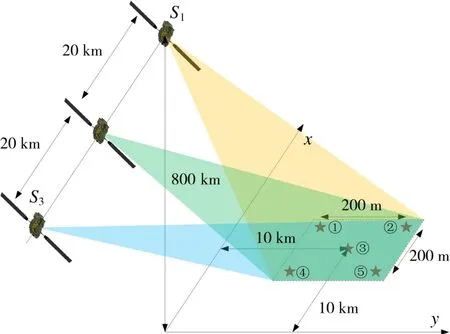
图6 分布式卫星凝视成像系统几何模型

表1 分布式卫星凝视成像系统仿真参数
卫星轨道高度为800 km,间距为20 km。场景中心位于(10 km,10 km)处,场景大小为200 m×200 m,5个目标点呈“×”型分布,顺序如图6所示。
基于以上模型与参数进行仿真,分别得到3部雷达的一维回波,如图7所示。
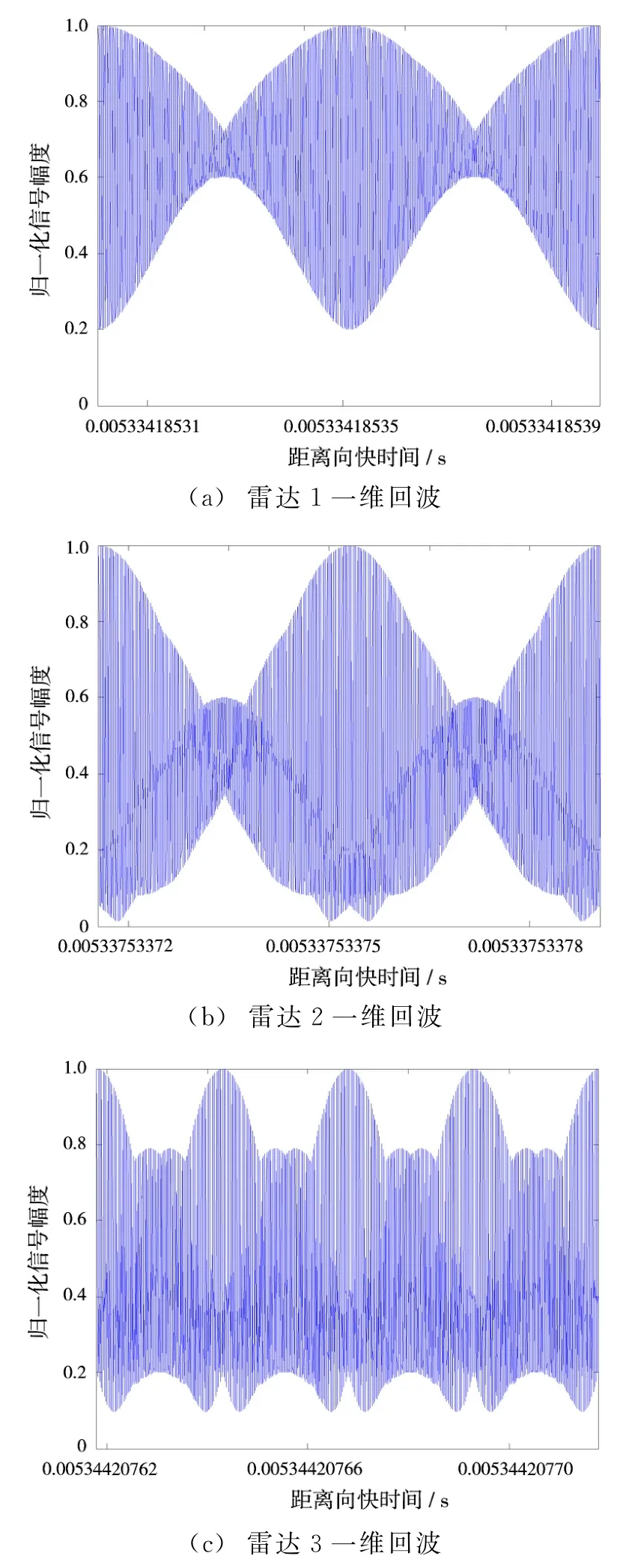
图7 分布式星载雷达一维回波
通过一维微波关联成像技术对雷达回波进行半径向压缩,所得结果如图8所示。
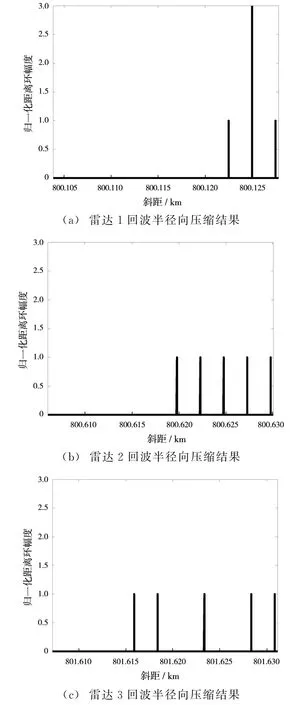
图8 雷达回波半径向压缩结果
然后将所得的所有距离环都映射到栅格化的场景中,其结果如图9所示。
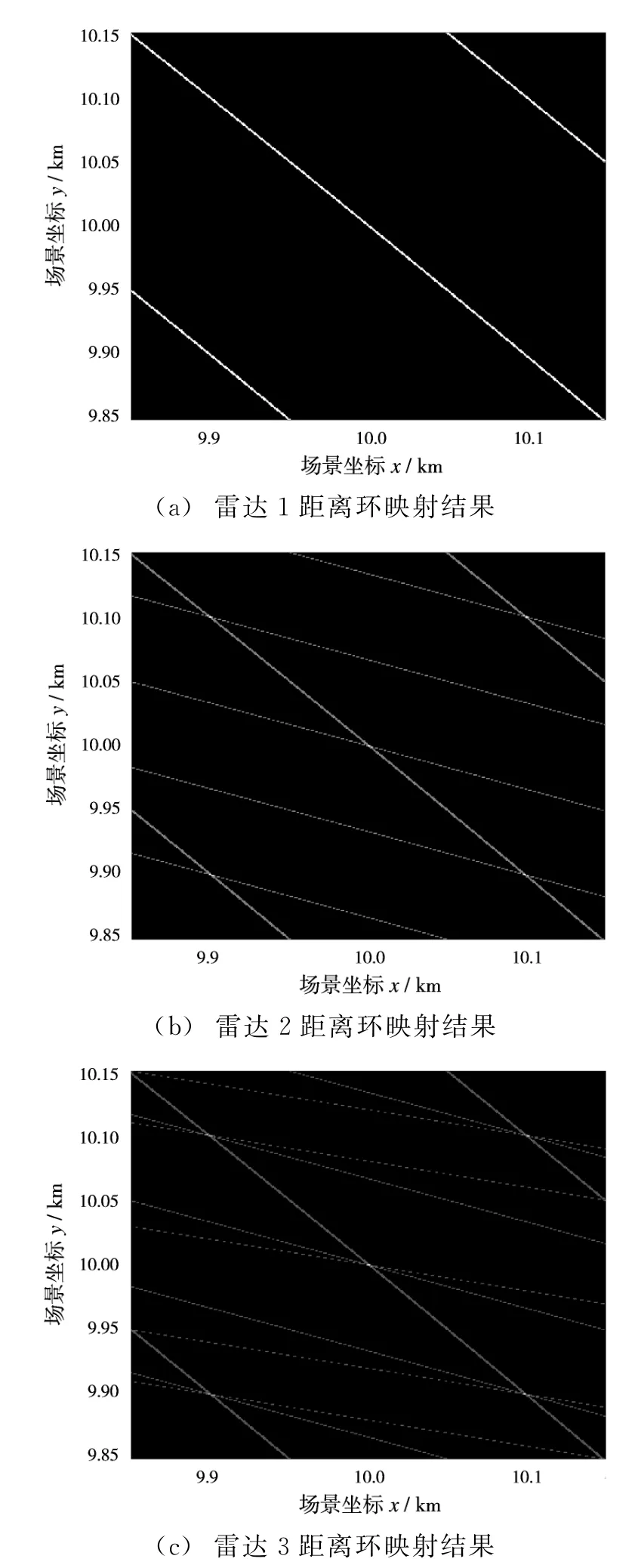
图9 距离环映射到场景
找出图像中同时位于3条距离环上的点,这些点即目标点所在的位置。最后根据各距离环幅度列写关于点目标幅度的方程组,解算出各目标点的幅度。最终的成像结果如图10所示。
可以看出,场景中的5个点目标得到了很好的聚焦。为探究成像性能,对各个点目标成像结果进行放大,如图11所示,其中沿x轴和y轴方向的分辨率已标出,x轴的平均分辨率为0.42 m,y轴的平均分辨率为1.16 m。5个点目标的分辨率如表2所示。
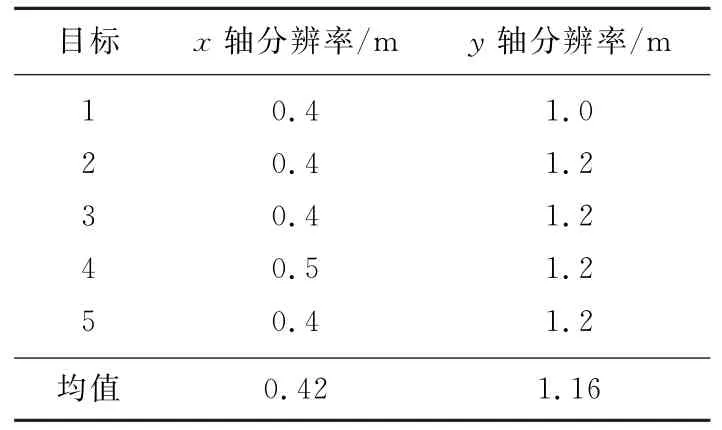
表2 各点目标分辨率
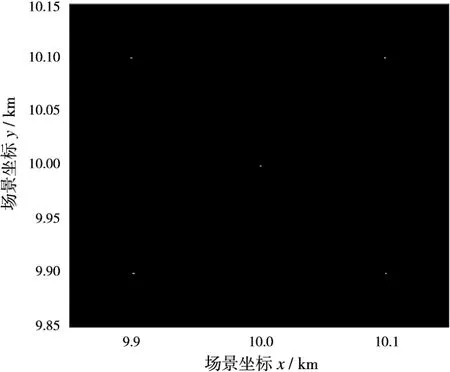
图10 分布式卫星凝视成像结果
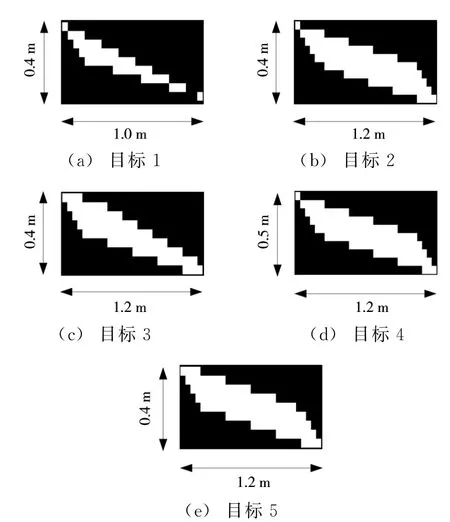
图11 各点目标成像结果及分辨率
4 结束语
在传统微波空间对地观测手段的基础上,结合新的微波关联成像理论,提出了一种基于一维微波关联成像技术的分布式卫星凝视成像方法。该方法不依赖雷达与目标的相对运动,比SAR成像具有更少的约束条件,且其回波形成仅需要一个脉宽的时间长度,可以实现准实时成像,相比于经典方法具有更高的成像效率。本文首先阐述了基于一维微波关联成像技术,实现各雷达回波的距离向压缩,获得目标距离环图像的方法;其次,给出了通过多颗分布式卫星,将距离环投影到栅格化场景中,求解目标的位置坐标的方法;然后,联立距离环幅度方程组,解算各目标点的幅度,从而达到对稀疏场景进行成像的目的;最后,通过试验仿真验证了该方法的可行性,各目标点聚焦良好,达到了较高的分辨率。
本文对这一方法体制进行了初步探究,该体制具有很大发展潜力,但存在一些关键问题需要解决。如超高采样率、超窄脉冲宽度、大系统功率等的物理实现;理论方面,分辨率与雷达个数及分布的关系、超多维方程组的求解、稀疏理论的应用等。这些都需进一步深入研究。
[1]CUMMING I G,WONG F H.Digital Processing of Synthetic Aperture Radar Data[M].Norwood,MA:Artech House,2005.
[2]保铮,刑孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2005.
[3]吴曼青.数字阵列雷达的发展与构想[J].雷达科学与技术,2008,6(6):401-405.WU Manqing.Development and Future Design of Digital Array Radar[J].Radar Science and Technology,2008,6(6):401-405.(in Chinese)
[4]李东泽.雷达关联成像技术研究[D].长沙:国防科学技术大学,2014.
[5]葛家龙.量子成像和量子雷达在遥感探测中的发展评述[J].中国电子科学研究院学报,2014,9(1):1-9.
[6]杨俊刚.利用稀疏信息的正则化雷达成像理论与方法研究[D].长沙:国防科学技术大学,2013.

