有源压制性干扰的干扰模糊区建模与仿真∗
罗金亮,金家才,朱 霖
(1.解放军电子工程学院302教研室,安徽合肥230037;2.安徽四创电子股份有限公司,安徽合肥230088)
0 引言
有源压制性干扰是一种通过发射噪声或类似噪声的强干扰信号,使雷达系统接收端信噪比严重降低,目标回波信号模糊不清或完全淹没在干扰信号之中而难以或无法判别的电子干扰。其只需要获取敌雷达信号少量的信息(雷达信号的频率及频率变化范围信息)便可以释放有效干扰,是一种易于实现的干扰方式,也是较为常用的一种干扰方式。
然而就如何对该类干扰效能进行高效、准确地评估,一直是界内不断探索且争论不休的难题,且目前也暂无统一定论。文献[1]总结了雷达干扰效果的评估准则,主要包括信息准则、功率准则、概率准则和时间准则;文献[2]与文献[1]相比又增加了战役-战术准则,其方法是通过战役或战术行动的整体作战效能的变化来反映雷达干扰效果;综合分析所查阅的所有文献,目前针对雷达有源压制性干扰的评估准则绝大多数采用功率准则,文献[3]利用干扰压制区的概念分析了掩护固定目标时的干扰波束内的压制区模型;文献[4]利用干扰扇面的概念进行了机载雷达有源干扰的扇面分析及模型建立。
上述研究成果极大程度地丰富了有源压制性干扰效果评估的方法,在一定程度上为有源压制性干扰的作战使用提供了参考,但综合分析上述研究成果,不难发现其评估结果均过于绝对,均采用“非此即彼”的描述,在实际中是否真的超过“干扰压制区”、“干扰扇面”或“干扰掩护区”的区域外边线就会立即暴露在敌雷达的探测威胁下呢?答案是否定的,因为干扰功率随距离的变化是一个渐进的过程,同时现代雷达的信号检测也是一个动态可调的过程,因此,当在实战或实测中不难发现,当被保卫目标的位置超越所估算的“干扰压制区”、“干扰扇面”或“干扰掩护区”的区域外边线时也不会立即被发现,而是要经过一个逐步被暴露的过渡区域即为干扰模糊区,在该区域内被保卫目标在雷达显示器中呈现“时现时隐”的模糊状态,无法被准确、连续地测定。
1 干扰模糊区的形成机理及模型构建
干扰模糊区是有效干扰区与暴露区之间的干扰效果逐步衰减,被保护目标逐渐被暴露的模糊过渡区域,它是干信比JSR与目标距离Rt之间呈连续反比关系的重要体现,其在现实中也是真实存在的。
1.1 干扰模糊区的形成机理
目前较为先进的雷达对目标回波信号的检测均是在基于一定发现概率Pd和虚警概率Pfa的条件下(恒虚警率CFAR),设定一个检测门限,如图1所示,当被检测信号电平大于或等于检测门限电平时,如图1中A点所示,雷达则认为此点有目标存在;当被检测信号电平小于检测门限电平时,如图1中B点所示,雷达则认为此点为噪声并在通过检波器时直接被滤除。然而通过检波器所被成功检录的信号中并非全为真实目标回波信号,若噪声信号超过检测门限并被判定为“目标”,则该“目标”便称为“虚警”。
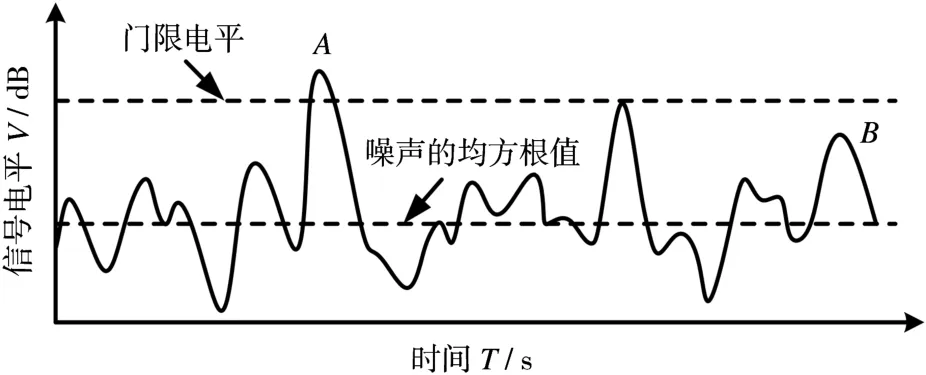
图1 雷达回波信号
有源压制性干扰通过向雷达发射噪声或类似噪声的干扰信号,以增大进入雷达接收机内信号中的噪声。当雷达接收机内噪声过大则将导致“虚警”过多时,雷达会相应地提高检测门限,以减少“虚警”,但随着检测门限的提高,相应一些能量较弱的真实目标回波信号也会被滤除,同时,由于雷达需要保证一定的发现概率,所以雷达也不可能过高地提高检测门限,因此,当对雷达施放较大功率的有源压制性干扰时,其将直接影响雷达信号检测,导致雷达检测门限相应提高,致使部分真实目标信号丢失,同时存在部分较大能量的噪声信号被雷达成功检录,致使在雷达屏幕上形成一定程度的“亮斑”,其“亮斑”的大小取决于进入到雷达接收机内的干信比JSR小。
在大多数文献中,将使雷达刚好失去正常工作能力的干扰信号功率与目标回波信号功率比值JSR定义为干扰压制系数Kj[5],针对雷达来说Kj通常为一个定值,其主要与雷达对信号检测性能相关,与外部干扰无关。为使干扰保持有效则必须使JSR≥Kj,经测试表明,常规脉冲雷达的干扰压制系数Kj通常为3~5 dB[6]。
根据干扰方程可得
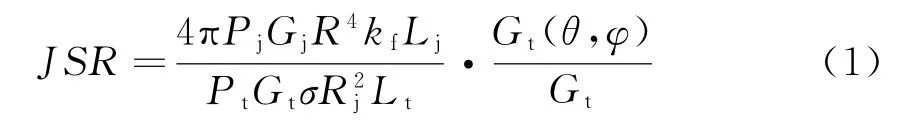
式中:JSR为进入到雷达接收机内的干信比;PtGt为雷达等效辐射功率;σ为被掩护目标的有效反射面;Rj为干扰机与雷达之间的距离;Lt为雷达信号在空中的传播损耗因子;PjGj为干扰机等效辐射功率;kf为雷达接收机有效通带宽度与干扰信号频谱宽度之比;Lj为干扰信号在空中的传播损耗因子;Gt为雷达天线主瓣增益;Gt(θ,φ)为偏离雷达主瓣方位角为θ,俯仰角为φ的副瓣增益。
从式(1)可以看出,在其他参数确定后,JSR与R4成正比,也就是说在作战过程中,当其他状态均保持不变的状态,随着被保卫目标与雷达之间的距离减小,雷达接收机内的干信比JSR也将逐渐减小,其关系如图2所示,从图中可以看出JSR与R之间的关系呈一条连续递增的曲线。
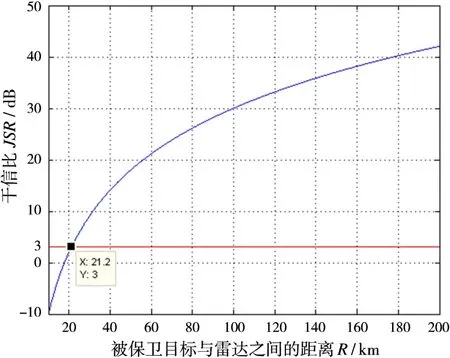
图2 JSR与R的关系
现假设雷达干扰压制系数为3 dB,根据图2可知,当被保卫目标与雷达之间的距离R≥21.2 km时,雷达将被有效压制,现需要解决下述两个问题:
1)需要论证是否R一旦小于21.2 km即为被保卫目标进入了“暴露区”呢?答案是否定的,因为根据图2的仿真结论,我们知道干信比JSR与R之间的关系呈一条连续递增的曲线,并不存在陡变的现象,因此,其干扰效果也应该是逐渐递减的过程。
2)干信比JSR要减小到什么程度才能彻底使雷达不受到干扰影响?根据图1我们知道在同一时刻t(即同一位置),当干扰信号与目标回波信号功率相等时,干扰信号依然能有效掩盖目标回波信号,反之则无效,由此可知,只要干信比JSR≥0,有源压制性干扰便具备有效掩护目标的可能。
综上所述,当干信比JSR逐步减小时,有源压制性干扰的干扰效果并非从“有效压制”直接跳入至“目标暴露”,其中间存在一定的过渡区域。在该过渡区域中,目标回波信号并非被干扰信号绝对掩盖,而是存在被掩盖的可能,目标时隐时现,其干扰效果是模糊的,因此,我们将该区域定义为干扰模糊区。
1.2 干扰模糊区的模型构建
1)干扰模糊距离Rm
根据上述对干扰模糊区的定义及其形成机理的描述,可得有源压制性干扰的干扰模糊区的数学模型为
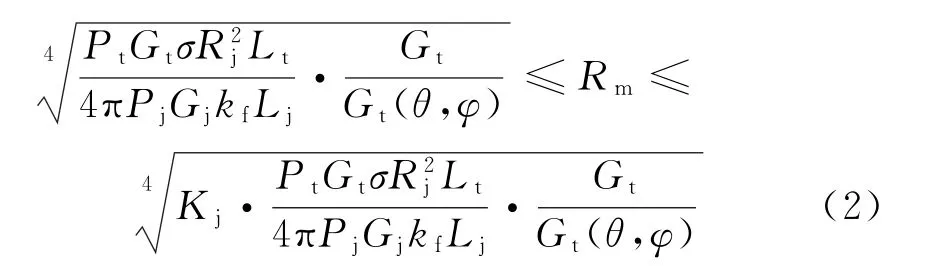
式中,Rm为雷达的干扰模糊距离。其余项与式(1)相同。
2)干扰压制系数Kj
雷达接收机的干扰压制系数是指接收机输入端线性分量的传输频带内使用压制干扰信号下的必需的最小干信比。其数学模型[7]为
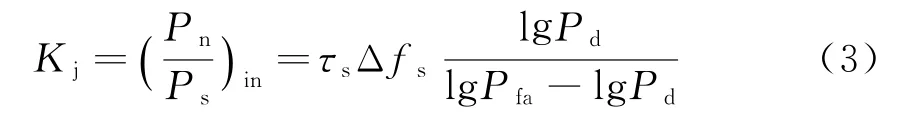
式中:τs为脉冲宽度;Δfs为频带宽度;Pd为雷达检测概率;Pfa为雷达虚警概率。
对于不同体制的雷达及其采用相应的抗干扰方法,其干扰压制系数均有所不同,具体情况详见表1[5]。

表1 各典型体制雷达或雷达抗干扰方法的干扰压制系数计算
3)天线副瓣增益Gt(θ,φ)
在雷达干扰效果评估过程中,雷达天线的方向性增益对准确评估的影响较大,然而雷达真实的雷达天线增益方向图只能通过实测获得,为实现对雷达干扰效果的有效评估,通常采用建立替代模型的方法进行雷达天线方向性增益进行估算。
由于有源压制性干扰可用于对任何类型的雷达实施干扰,既可以是预警雷达也可以是制导(火控)雷达,由于本文主要探讨有源压制干扰的干扰模糊区,而预警雷达与制导(火控)雷达相比,其探测距离及受到相同干扰时所呈现的干扰区域范围都要略大,因此,为更显著地展示干扰模糊区的效果,选定对预警雷达进行干扰评估建模。由于现有主战预警雷达大多采用余割平方天线。
其在方位平面上天线波束的主瓣方向图一般为高斯型,而主瓣以外的方向图为辛格函数形式,其方向图函数为
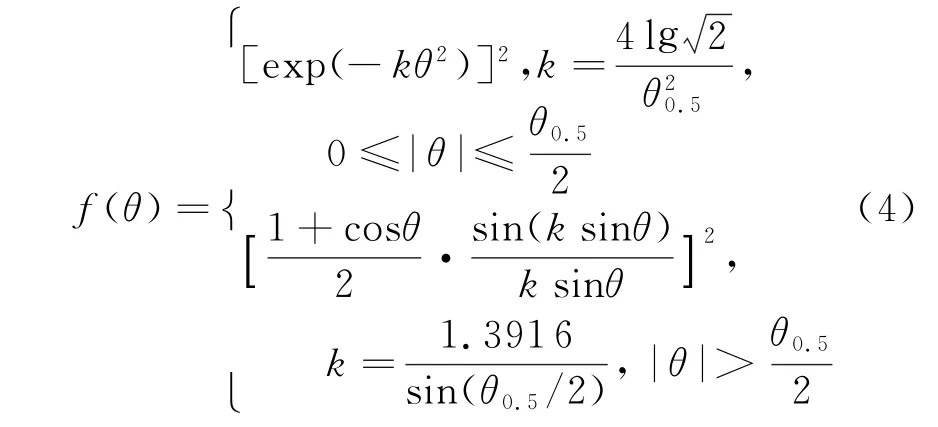
式中:f(θ)为雷达方向图函数;θ0.5为雷达在方位平面上的半功率波瓣宽度。
设θ0.5=3.8°,根据式(4)对雷达天线方向图进行仿真,得到余割平方天线方位平面的方向图如图3所示。
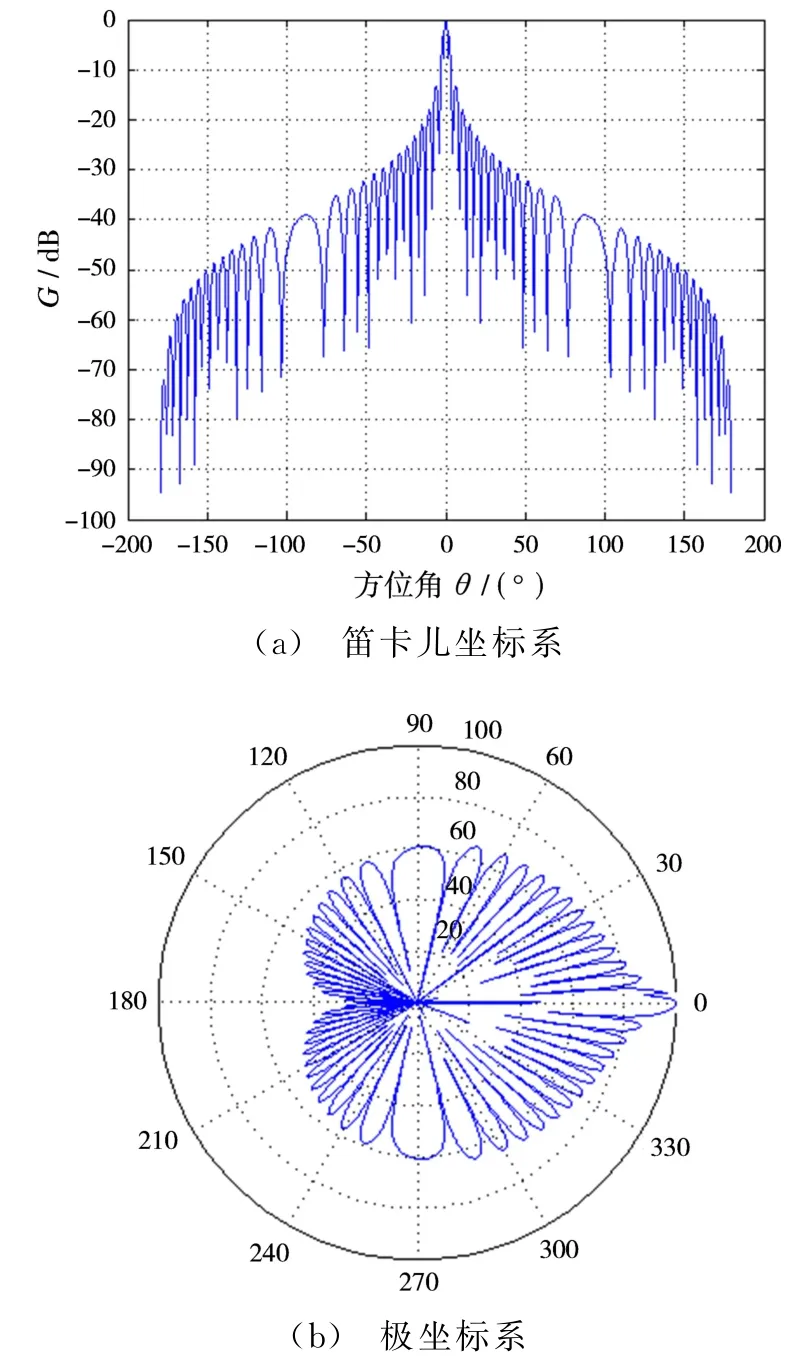
图3 θ0.5=3.8°雷达天线方位平面的方向图
其在俯仰平面上天线波束的主瓣方向图一般为余割平方形,其方向图函数为
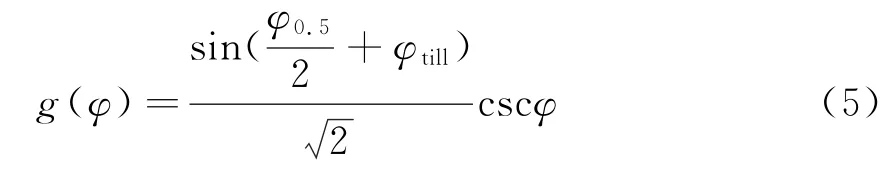
式中:φ0.5为雷达在俯仰平面上的半功率波瓣宽度;φtill为主瓣相对于水平面上仰的角度。
设φ0.5=8°,φtill=7°,根据式(5)对雷达天线方向图进行仿真,得到余割平方天线俯仰平面的方向图如图4所示。
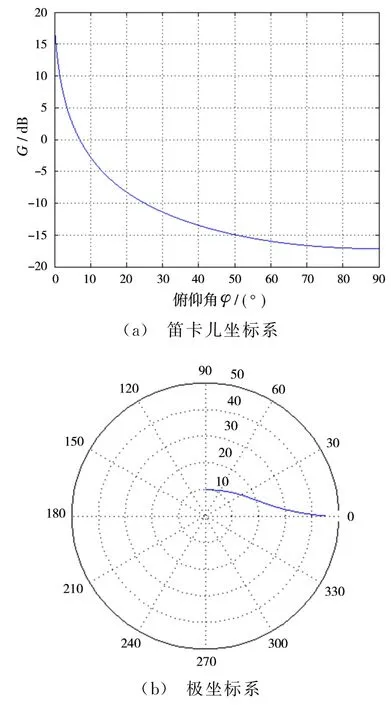
图4 θ0.5=8°雷达天线俯仰平面的方向图
综上所述,天线副瓣增益Gt(θ,φ)应为
Gt(θ,φ)=f(θ)·g(φ) (6)
根据式(6)对雷达天线方向图进行仿真,得到余割平方天线立体方向图如图5所示。
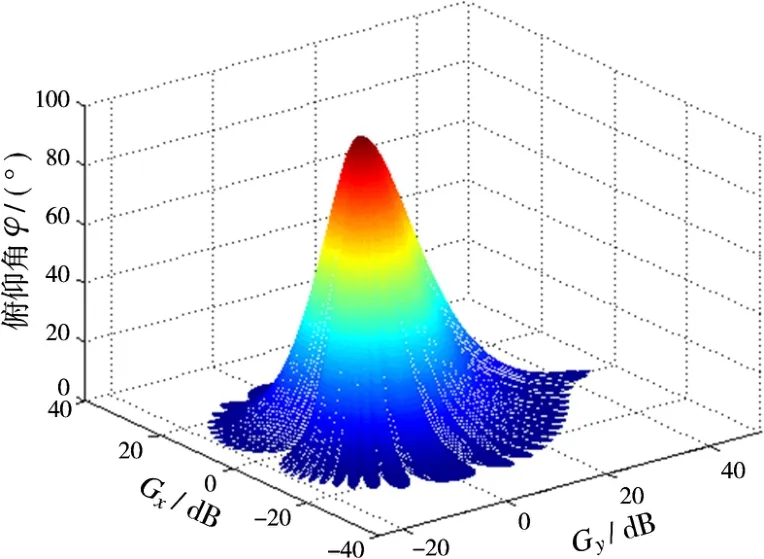
图5 θ0.5=3.8°,φ0.5=8°雷达天线方向图
2 干扰模糊区的仿真分析
现以航空电子对抗力量采取远程支援干扰方式,对敌地面远程预警雷达实施有源压制性干扰,以掩护我航空兵实施突防为背景,进行干扰模糊区的仿真分析。
2.1 单部雷达干扰模糊区仿真分析
以干扰美AN/TPS-44预警雷达为例,设其Pt=1.12 k W,Gt=29 dB,θ0.5=3.8°,φ0.5=8°,Kj=3 d B;设干扰机Pj=1 k W,Gj=27 d B,R′j=1.5×105m,Hj=6000 m,kf=10;突防飞机σ=10 m2,Ht=150 m;信号在空气中的传播衰减不计。
通过Matlab仿真,结果如图6所示。
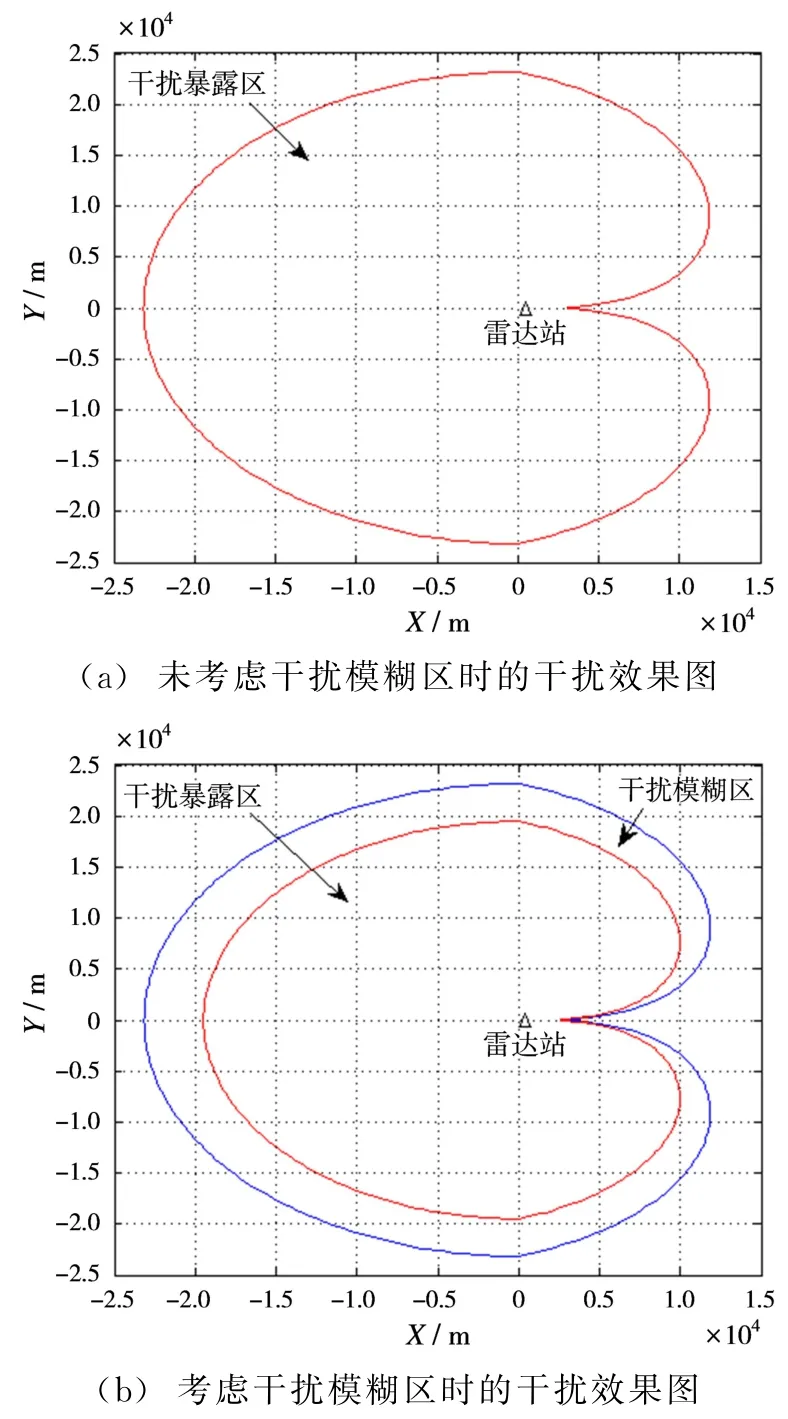
图6 单部雷达干扰模糊区仿真结果图
图6(a)显示的是未考虑干扰模糊区时的干扰效果图,“心”形线内所围成的区域为“干扰暴露区”,“心”形线外的其他区域均为“有效压制区”;图6(b)显示的是加入干扰模糊区时的干扰效果图,小“心”形线内所围成的区域为“干扰暴露区”,小“心”形线外与大“心”形线内所夹的区域为“干扰模糊区”,大“心”形线外的其他区域为“有效压制区”。
根据仿真结果可以看出,若未考虑“干扰模糊区”的实际存在,则在估算干扰暴露区时,其范围将明显增大,在绝大部分方向上扩大纵深约达5 km,在该区域内预警雷达并不能准确、连续地探测目标,在雷达显示屏上会因干扰产生大量的“点迹”,从而有效掩盖了真实目标回波信号。在实战中若舍弃“干扰模糊区”这一概念,在作战筹划阶段,筹划兵力数量及装备性能时,将会提出过高需求(干扰机功率需求将高出1倍),这将是对兵力运用的极大浪费。
下面对干扰机处于不同距离位置,对干扰模糊区进行仿真,设Rj分别为200,150,100和50 km,结果如图7所示。
从仿真结果可以看出,随着干扰机与雷达之间的距离不断缩小,干扰掩护区的范围也在逐渐缩小,根据式(2)可以知道,这是由于Rm∝Rj所造成的。

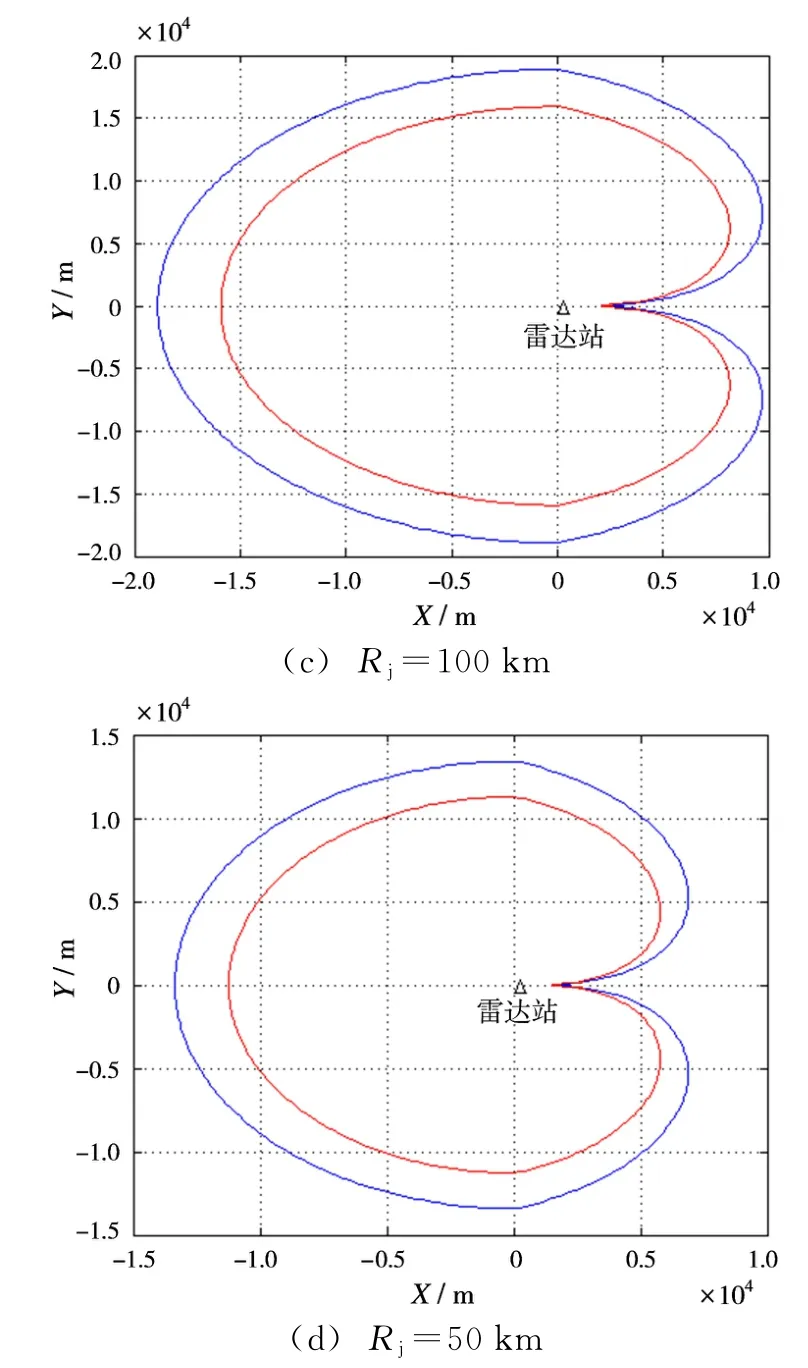
图7 干扰机处于不同距离时的干扰模糊区仿真结果图
2.2 组网雷达干扰模糊区仿真分析
在实际作战过程中,干扰机所面对并不是单一的某部雷达,而是相互交织的雷达网,下面针对两种典型配置形式的雷达网进行干扰模糊区的仿真分析。
1)“一线”配置
根据超短波的最大通信距离,设雷达站站距为20 km,各雷达站的坐标分别为A1:(0,0)、A2:(0,2×104)、A3:(0,-2×104),并不断减少干扰机与雷达阵地间的间距,仿真结果如图8所示。
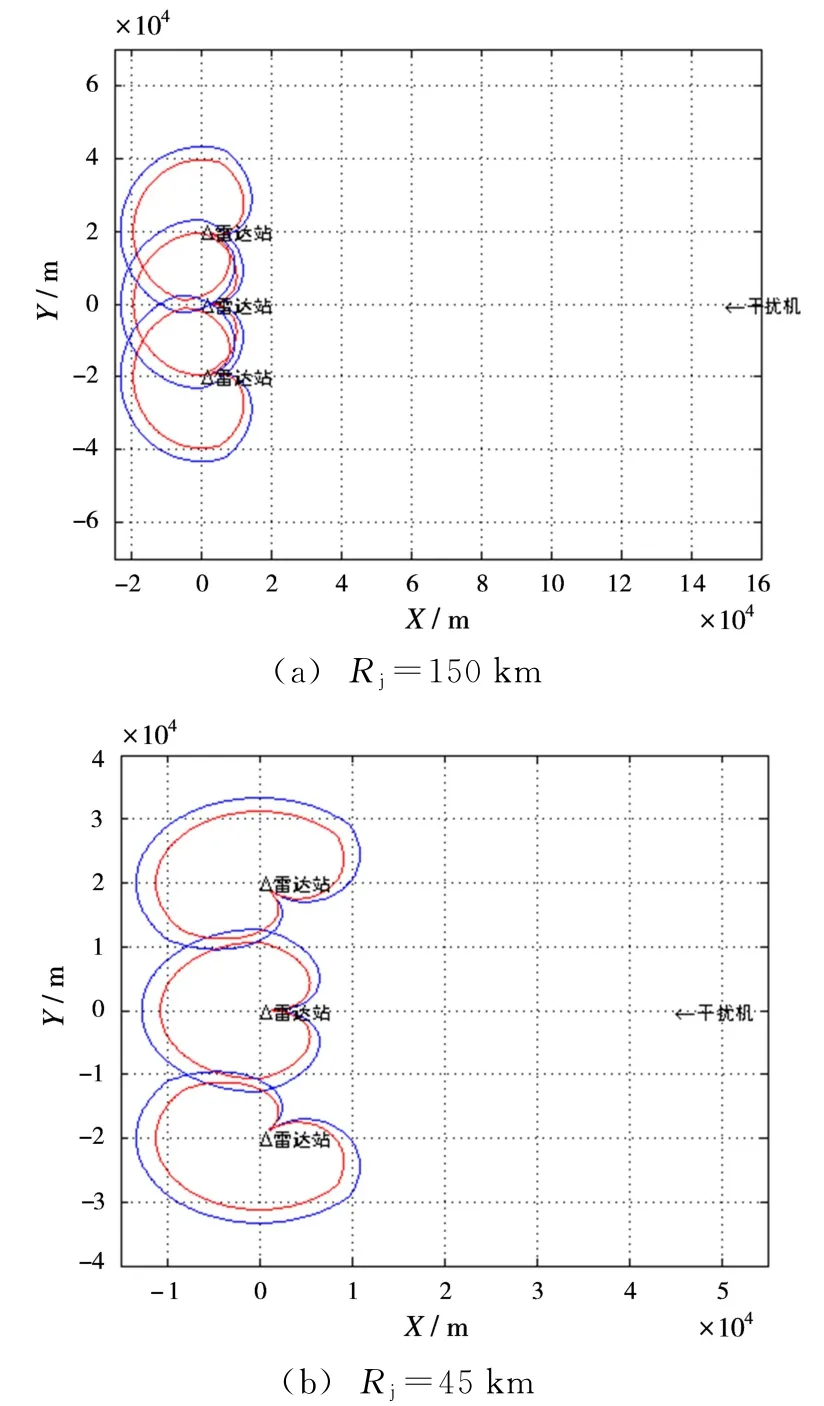
图8 呈“一线”配置雷达网干扰模糊区仿真结果图
从仿真结果可知,随着干扰机与雷达阵地之间的距离不断减小,雷达网的有效探测区域逐渐减小,当Rj≤45 km时,雷达网的“干扰暴露区”已不存在交叉重叠区,但“干扰模糊区”仍存在交叉重叠区,突防飞机可以选择该区域作为“通道”进行突防。
2)“倒三角”配置
设雷达站站距为20 km,各雷达站的坐标分别为A1:(0,1×104)、A2:(0,-1×104)、A3:(-2×104×sin60°,0),仿真结果如图9所示。
从仿真结果可知,当Rj≤40 km时,呈“倒三角”配置的雷达网才出现具备实施突防条件的“突防通道”,这是由于干扰机对雷达网中的前两部雷达均是从副瓣实施干扰,其比主瓣干扰需要更大的能量,所以其要求的干扰机距离需更近,因此,面对敌“倒三角”雷达网不应选择“三角”的一边中线作为突防方向,而应选择威胁较弱的“一角”实施干扰并突防。
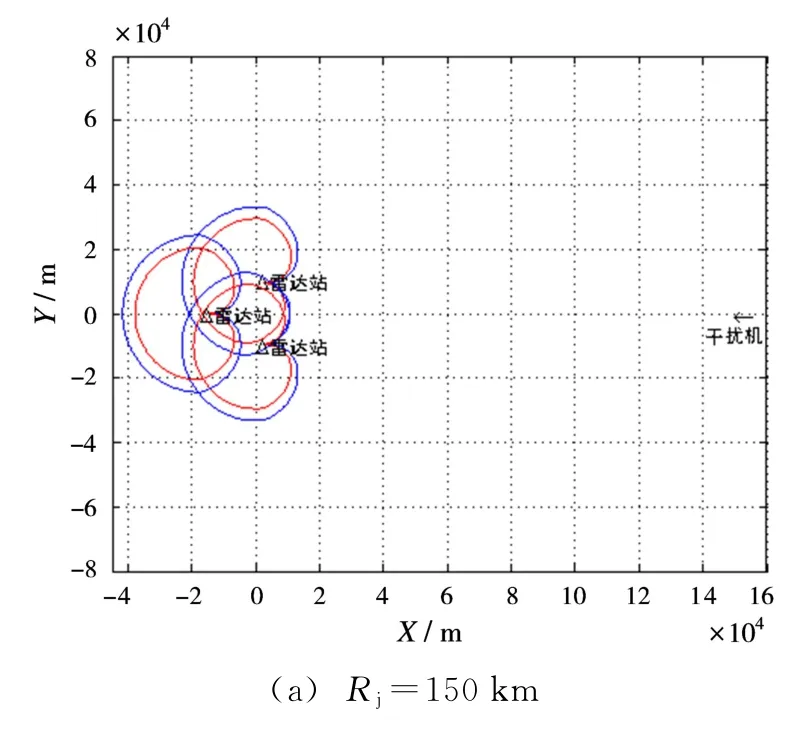
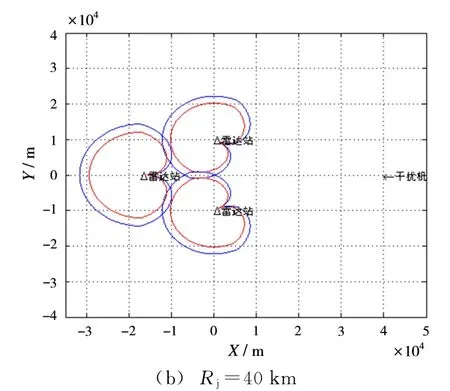
图9 呈“倒三角”配置雷达网干扰模糊区仿真结果图
3 结束语
本文在分析当前对有源压制性干扰评估方法不足的基础上,提出了“干扰模糊区”的概念,并对其进行了数学建模及仿真分析,在后续的实装测试中也验证了该区域的真实存在,进行“干扰模糊区”的计算可为实战中更为精准的使用兵力及作战态势的评估提供参考。由于在本文建模过程中,没有对被保卫目标的各状态的RCS及信号在环境传播中的损耗进行分析,因此,根据该模型计算的结果与实际情况略有出入。目前,“干扰模糊区”还处于初步探讨阶段,如何选择更为有效的干扰信号调制方式及干扰样式以提高干扰机在“干扰模糊区”内的干扰掩护效果,将是下一步需要继续深入研究的问题。
[1]张崔永,赵风东,杨志祥.新型干扰样式对某型雷达干扰效果研究[J].雷达科学与技术,2013,11(3):241-245.
[2]刘南辉.俄罗斯空军电子对抗作战效能评估[M].北京:中国人民解放军空军,2007.
[3]康亚光,秦开兵,游志刚.固定目标防护的干扰波束内部压制区模型分析[J].火力与指挥控制,2012,37(4):114-116.
[4]平殿发,刘志远,张韫.机载雷达有源干扰扇面分析与估算[J].雷达科学与技术,2012,10(4):443-447.
[5]赵国庆.雷达对抗原理[M].2版.西安:西安电子科技大学出版社,2012.
[6]张锡祥,刘永坚,王国宏.和平时期电子战技术与应用:雷达对抗篇[M].北京:电子工业出版社,2005.
[7]VAKIN S A,SHUSTOV L N,DUNWELL R H.Fundamentals of Electronic Warfare[M].Norwood,MA:Artech House,2001.

