给分式方程应用题归归类
王康康


学习了分式方程的有关内容,同学们还必须得熟练运用分式方程解决实际生活中的问题.常见的实际问题有营销类应用性问题、工程类应用性问题、行程类应用性问题等几大类,这些题目看似复杂,但只要抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节,正确列出方程,再进行求解即可.不过同学们一定要注意的是,得出方程的解后,一要检验所求的解是否是原方程的解,二要检验所求的解是否符合题意,三要注意检验和解释结果的合理性.
一、营销类应用性问题
例1 某校办工厂将总价值为2 000元的甲种原料与总价值为4 800元的乙种原料混合后,其单价比原甲种原料每斤少3元,比原乙种原料每斤多1元,问:混合后的原料每斤是多少元?
分析:市场经济中,常遇到营销类应用性问题,这类问题中与价格有关的量是单价、总价、平均价等,要了解它们各自的意义,从而建立它们之间的关系式.
解:设混合后的原料单价为每斤 [x]元,则原甲种原料的单价为每斤([x]+3)元,原乙种原料的单价为每斤([x]-1)元,混合后的总价值为(2 000+4 800)元, 混合后的重量为[2 000+4 800x]斤,甲种原料的重量为[2 000x+3]斤,乙种原料的重量为[4 800x-1]斤, 依题意,得
[2 000x+3]+[4 800x-1]=[4 800+2 000x]
解得
[x]=17
经检验,[x]=17是原方程的根.
所以[x]=17. 即混合后的原料每斤 17元.
总结:营销类应用性问题,涉及进货价、售货价、利润率、单价、混合价、赢利、亏损等概念,要结合实际问题对它们各自表述的意义有所了解.同时,要掌握好基本公式,巧妙建立关系式.这类问题与现实生活息息相关,因而成为中考常考的热点问题.
【练习1】
A、B两名采购员去同一家饲料公司购买同一种饲料两次,两次饲料的价格有变化.两名采购员的购货方式不同,其中采购员A每次购买1 000千克,采购员B每次用去800元而不管购买饲料多少,问:谁的购货方式合算?为什么?
二、工程类应用性问题
例2 某工程由甲,乙两队合做6天完成,厂家需付甲,乙两队共8 700元;乙,丙两队合做10天完成,厂家需付乙,丙两队共9 500元;甲,丙两队合做5天完成全部工程的[23],厂家需付甲,丙两队共5 500元.
(1)求:甲,乙,丙各队单独完成全部工程各需多少天?
(2)若工期要求不超过15天完成全部工程,问:由哪个队单独完成此项工程花钱最少?请说明理由.
分析:这是一道联系实际生活的工程应用题,涉及工期和工钱两种未知量.对于工期,一般情况下把整个工作量看成1,设甲,乙,丙各队完成这项工程所需时间分别为x天,y天,z天,可列出分式方程组.
解:(1)设甲队单独做需x天,乙队单独做需y天,丙队单独做需z天,依题意,得
[ 6([1x+1y])=1
10([1y]+[1z])=1
5([1x]+[1z])=[23] ]
[解得x=10y=15z=30]
经检验,[x]=10,[y]=15,[z]=30是原方程组的解.
(2)设甲队做一天厂家需付a元,乙队做一天厂家需付b元,丙队做一天厂家需付c元,根据题意,得
[6(a+b)=8 70010(b+c)=9 5005(c+a)=5 500 ]
[解得a=800b=650c=300]
由(1)可知完成此工程不超过既定工期只有两个队:甲队和乙队.
此工程由甲队单独完成需花费10a=8 000元;此工程由乙队单独完成需花费15b=9 750元.
所以,由甲队单独完成此工程花钱最少.
技巧点拨:在(1)的求解时,把[1x],[1y],[1z]分别看成一个整体,可把分式方程组转化为整式方程组来解.
【练习2】
某工程需在规定日期内完成,若由甲队去做,恰好如期完成;若由乙队去做,要超过规定日期3天才能完成.现由甲、乙两队合做2天,剩下的工程由乙队独做,恰好在规定日期内完成,问:规定的日期是多少天?
【练习3】
今年某大学在招生录取时,为了防止数据输入出错,2 640名学生的成绩数据由两位教师分别向计算机输入一遍,然后让计算机比较两人的输入是否一致.已知教师甲的输入速度是教师乙的2倍,结果甲比乙少用2小时输完.问:这两位教师每分钟各能输入多少名学生的成绩?
三、浓度应用性问题
例3 有含盐15%的盐水40千克,要使盐水含盐20%,还需要加入多少千克盐?
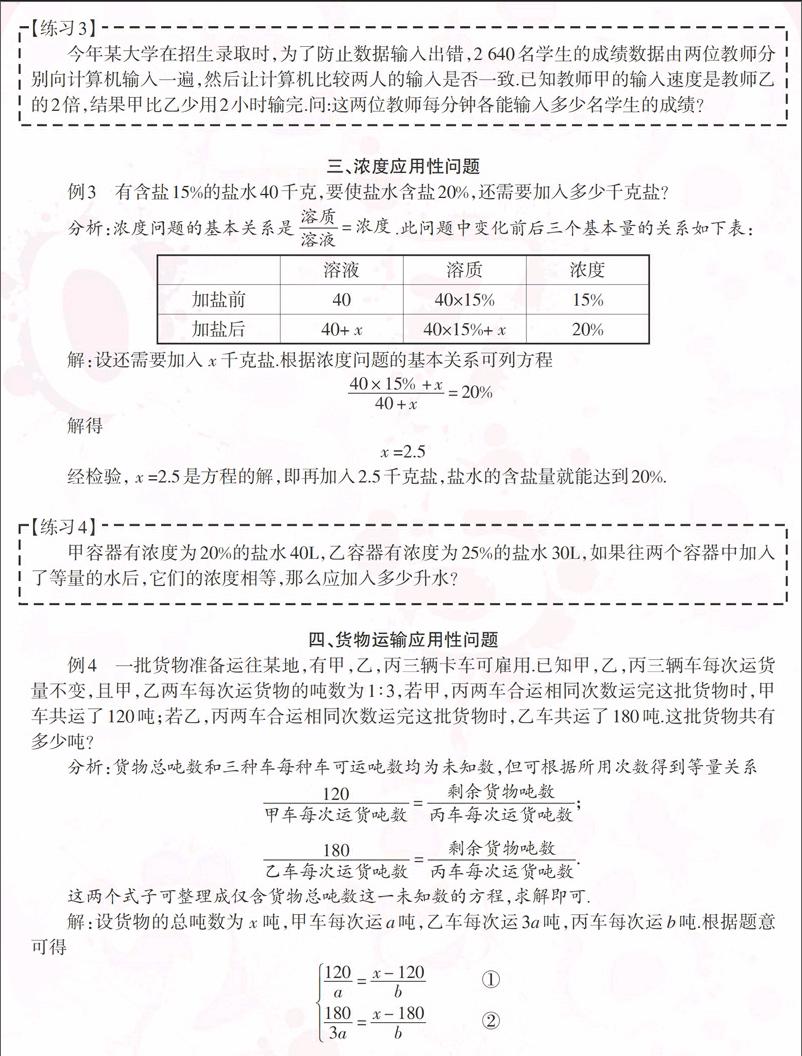
分析:浓度问题的基本关系是[溶质溶液=浓度].此问题中变化前后三个基本量的关系如下表:
[\&溶液\&溶质\&浓度\&加盐前\&40\&40×15%\&15%\&加盐后\&40+[x]\&40×15%+[x]\&20%\&]
解:设还需要加入[x]千克盐.根据浓度问题的基本关系可列方程
[40×15%+x40+x=20%]
解得
[x]=2.5
经检验,[x]=2.5是方程的解,即再加入2.5千克盐,盐水的含盐量就能达到20%.
【练习4】
甲容器有浓度为20%的盐水40L,乙容器有浓度为25%的盐水30L,如果往两个容器中加入了等量的水后,它们的浓度相等,那么应加入多少升水?
四、货物运输应用性问题
例4 一批货物准备运往某地,有甲,乙,丙三辆卡车可雇用.已知甲,乙,丙三辆车每次运货量不变,且甲,乙两车每次运货物的吨数为1∶3,若甲,丙两车合运相同次数运完这批货物时,甲车共运了120吨;若乙,丙两车合运相同次数运完这批货物时,乙车共运了180吨.这批货物共有多少吨?
分析:货物总吨数和三种车每种车可运吨数均为未知数,但可根据所用次数得到等量关系
[120甲车每次运货吨数=剩余货物吨数丙车每次运货吨数;]
[180乙车每次运货吨数=剩余货物吨数丙车每次运货吨数.]
这两个式子可整理成仅含货物总吨数这一未知数的方程,求解即可.
解:设货物的总吨数为[x]吨,甲车每次运a吨,乙车每次运3a吨,丙车每次运b吨.根据题意可得
[120a=x-120b ①1803a=x-180b ②]
解得
[x]=240
经检验,[x]=240是方程的解,即这批货物共有240吨.
【练习5】
五、行程中的应用性问题

