基于静态贝叶斯博弈的风险评估方法研究

基于静态贝叶斯博弈的风险评估方法研究*

余定坤，王晋东，张恒巍，王娜，陈宇

(解放军信息工程大学密码工程学院,河南 郑州 450000)

摘要：目前基于博弈论的风险评估方法大多数采用完全信息博弈模型，无法应对攻击者和防御者互不清楚对方行为的情况。基于静态贝叶斯博弈理论建立攻防博弈模型，将攻击者和防御者分为多种类型，全面地分析了博弈的贝叶斯均衡及其存在性，并结合防御者反击行为、攻击成功率对已有的策略收益量化方法进行改进。基于博弈均衡进行攻击行为可信预测，给出了风险评估算法对信息系统所存在的风险进行计算，得到系统风险值。最后，通过一个实例分析验证了模型和算法的有效性。

关键词：风险评估;静态贝叶斯博弈;收益量化;混合策略;贝叶斯均衡

中图分类号：TP309 文献标志码：A

doi:10.3969/j.issn.1007-130X.2015.06.008

收稿日期：*2014-08-11;修回日期：2014-09-28

基金项目：国家自然科学基金资助项目(61303074，61309013)；国家973计划资助项目(2012CB315900)

作者简介:

通信地址：450000 河南省郑州市高新区科学大道62号33分队

Address:The PLA Information Engineering University,62 Kexue Avenue,High-tech Industrial Development Zone,Zhengzhou 450000,Henan,P.R.China

Risk assessment selection based on static Bayesian game

YU Ding-kun，WANG Jin-dong，ZHANG Heng-wei，WANG Na，CHEN Yu

(College of Cryptography and Engineering,The PLA Information Engineering University,Zhengzhou 450000,China)

Abstract:Nowadays,most studies of risk assessment methods based on game theory use complete information game model.These models cannot deal with the situation in which the attacker and the defender do not know each other’s actions.In this paper we establish an attack-defense model based on static Bayesian game theory to categorize the attacker and the defender into different types.Then,we analyze the Bayesian equilibrium of the game comprehensively,and improve the taxonomy and cost quantitative method of the classical strategies with consideration of the strike back acts of the defender and the success rate of attacks.Under the premise that the actions of the attacker are predicted based on game equilibrium,we use the risk calculating algorithm to calculate the risk in the information system. Simulation results prove the effectiveness of the proposed model and the algorithm.

Key words:risk assessment;static Bayesian game;cost quantitative method;mixed strategy;Bayesian equilibrium

1引言

网络技术的不断发展，给人们的生活带来了翻天覆地的变化，但由于其互联性、多样性、开放性，网络中的风险无处不在，使网络很容易受到来自各方攻击的威胁。网络遭受攻击会对网络中的用户产生巨大影响，蒙受巨大损失。若能够对风险进行评估，并根据评估结果在风险发生之前采取有效措施降低风险，使风险发生概率降低，则可以很好地提高网络的安全性。

近年来，不少专家学者对风险评估进行研究，使得风险评估技术更加科学、合理。文献[1]采用BP(Back Propagation)神经网络方法对信息交互风险概率进行预测，存在的问题是神经网络对大样本数据学习的速度较慢，导致预测模型缺乏实时性。文献[2]提出一种基于人工免疫的网络安全实时风险检测方法，在网络系统面临攻击时对其进行实时风险评估，该方法存在的问题是仅得到系统实时的风险值，并未对未来的风险进行可靠预测。文献[3]提出了一种用于实时风险概率预测的马尔可夫时变模型，通过更新状态转移矩阵来预测未来时刻网络的风险值，存在的问题是状态概率转移矩阵不易确定。另外，这些方法存在的共同问题是仅从防御者的角度出发，独立地考虑系统所面临的风险，是片面、不科学的。文献[4]建立博弈模型对网络脆弱性进行评估，存在的问题是采用完全信息静态博弈模型，与网络实际不够贴近。文献[5]建立博弈模型对网络风险进行量化评估，存在的问题是成本量化方法较简单，且基于完全信息静态博弈模型。

目前，博弈论在风险评估领域的应用大多数采用完全信息博弈模型。此类博弈模型只需根据策略进行策略收益量化形成收益矩阵即可计算Nash均衡，具有计算简单的优点。但是，网络的现实情况是攻击者和防御者不一定能互相清楚对方策略及收益，针对这样的情况，基于完全信息博弈模型的作用会十分有限。因此，本文提出基于静态贝叶斯博弈模型的风险评估方法，对风险进行评估。

2静态贝叶斯博弈模型

静态贝叶斯博弈是不完全信息同时行动的博弈，其中同时行动是指所有参与者同时选择自己的行动或者是后行动者不知道先行动者采取了什么行动；而不完全信息指在博弈时至少有一个参与者不能确定其他参与者的收益函数，参与者的收益函数对应着该参与者的类型[6]。

2.1模型假设

假设1(理性假设)假设攻防双方在完全理性的前提下进行攻防对抗，无论是攻击者还是防御者，在行动时，都需要理性考虑成本与收益的关系，都不会采取不计代价的行动。

假设2(类型假设)假设攻击者和防御者将对另一方策略收益的不确定看作是对另一方类型的不确定，但对另一方的类型的概率分布有一个判断[6]。

假设3(收益假设)假设攻防双方收益基于信息资源的经济价值进行收益量化。当前，基于信息经济学的收益量化研究较多，且较成熟。因此，基于信息资源经济价值进行收益量化有成熟理论作支撑，结果会更加科学、合理。

2.2模型相关定义

定义1静态贝叶斯博弈模型SBGM(Static Bayesian Game Model)是一个五元组SBGM=(N,T,M,P,U)，其中

(1)N=(N1,N2,…,Nn)是博弈的参与者集合。参与者是参与博弈的独立决策、独立承担结果的个人或组织，在不同的场合中，参与者的定义是不同的。在本文中，参与者是攻击者和防御者。

(4)P=(P1,P2,…,Pn)是参与者的先验信念集合。Pi=Pi(t-i|ti)表示参与者i在自己实际类型为ti的前提下，对其他参与者类型(若有多个参与者时为类型组合)t-i的判断。

(5)U=(U1, U2,…, Un)是参与者的收益函数集合。收益函数表示参与者从博弈中可以得到的收益水平，由所有参与者的策略共同决定，参与者不同的策略组合所得到的收益不同。

以上给出了SBGM模型的通用模型。为了简化分析，本文只考虑n=2的情况，SBG-ADM=((NA,ND), (TA,TD), (MA,MD), (PA,PD), (UA,UD))。其中,

(1)NA表示攻击者，ND表示防御者，为信息安全攻防博弈的两个参与者。

(4)PA(tD|tA)指攻击者的类型为tA时，其对防御者类型tD的一个概率判断；PD(tA|tD)指防御者类型为tD时，其对攻击者类型tA的一个概率判断。

(5)∀mA∈MA,mD∈MD,tA∈TA,tD∈TD，UA(mA,mD,tA)表示防御者采用行动mD抵御攻击者的攻击行动mA时且攻击者类型为tA时，攻击者的收益；UD(mA,mD,tD)表示防御者采用行动mD抵御攻击者的攻击行动mA时且防御者类型为tD时，防御者的收益。

2.3策略收益量化

网络中攻击者和防御者策略成本收益量化是网络最优防御策略选取的基础，其量化是否合理直接影响网络防御策略选取结果。姜伟等人[8]在总结多种攻击防御策略分类的基础上，提出了一种成本/收益量化方法。 陈永强等人提出了一种根据意图对策略成本/收益进行量化的方法。本文对以上策略收益量化方法进行改进，使得量化结果更加科学、合理。

定义2系统损失代价Dcost(Damage cost)表示某类攻击对目标资源的损害程度；攻击致命度AL(Attack Lethality)表示某类攻击所具有的固有危害程度；攻击成本AC(Attack Cost)表示攻击者发动一次攻击所需要的软硬件资源、专业知识等；防御成本Decost(Defense cost)是防御策略的操作代价、负面代价和残余代价之和。一般可将防御者的损失Dcost作为攻击者的所得。详细定义见文献[8]。

定义3防御回报DR(DefenseReward)表示针对某一攻击策略采取防御策略后防御者的回报情况。在文献[8]中表示为针对某一攻击采取防御策略，网络系统免受的损失。本文认为，防御回报分为两种情况:

定义4(攻击间接收益SM)攻击直接收益是指攻击成功后，攻击者所能获得的即时效益。而攻击间接收益SM是指攻击成功后，一段时间内防御者可能遭受的社会损失，例如用户流失、服务质量下降等，需要评估人员根据评估环境、评估要求的不同而进行确定。攻击者获得间接收益的同时，防御者面临着间接损失，同样为SM。

攻击成功时双方收益情况：

Dcost-μ·DR′-AC + SM

(1)

-Dcost + μ·DR′-Decost-SM

(2)

攻击失败时双方收益情况：

(3)

(4)

攻击策略的成功率为SARi，由此可得到双方在此网络场景中的收益期望：

(5)

(6)

其中,ae为该攻击策略所包含的原子攻击；i、j分别为攻击者、防御者采取的第i、j个行动。

攻击者和防御者的收益之和为：

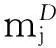
以上博弈场景双方的收益之和为：

由上述推导过程容易知道，无论攻击者攻击还是不攻击，攻击者与防御者的博弈收益之和为一个不为零的常数，则此博弈为非零和博弈。攻击者进行攻击为了得到防御者的有价值的信息，防御者则希望能够抵御这种攻击，在这个过程中，双方都需要付出相应代价。而攻击者不攻击时，防御者进行了防御，则防御者需要付出相应的防御代价。

2.4博弈均衡分析

3基于静态贝叶斯博弈的风险评估

3.1基于静态贝叶斯博弈的风险评估方法

对信息系统风险进行预测涉及到资产、威胁、弱点和风险四个要素。基于以上四个要素，给出风险计算模型，如图1所示。

Figure 1　Model of risk calculation 图1　风险计算模型

风险计算公式为：

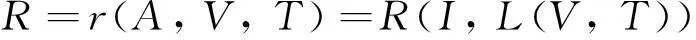
(7)

其中,R表示风险；A表示资产；V表示资产脆弱性；T表示威胁；I表示威胁造成安全事件后对组织业务的影响；L表示威胁利用资产的脆弱性造成安全事件发生的可能性。

由公式(1)可以看出，我们可以通过分析威胁发生的可能性L及威胁发生的可能后果I来对风险进行预测。

风险评估需要在双方并不完全知道对方信息的情况下综合考虑攻击者的攻击行动及防御者的防御行动的成本和代价，是一个复杂的过程。基于静态贝叶斯博弈进行风险评估可以很好地处理这一类问题。

信息系统是由多个风险子域组成的，各个风险子域之间共享同一个防御策略库。攻击者之间的关系是独立的，攻击者可与风险子域的防御者建立攻防博弈场景。

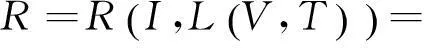
(8)

考虑计算各个风险子域的风险情况，可得到各个风险子域的风险向量(R1,R2, …, Rn)。假设各个安全风险子域的资产价值向量为A=(A1,A2, …,An)，将其归一化可得到权向量W=(w1,w2, …,wn)，则可得到信息系统的整体风险为：

(9)

3.2基于静态贝叶斯博弈的风险评估算法

算法1基于静态贝叶斯博弈的风险评估算法

输入：SBGM;

输出：信息系统整体风险RALL。

BEGIN

1. 初始化SBGM((NA,ND), (TA,TD), (MA,MD), (PA,PD), (UA,UD))；

2. 构建攻击者、防御者类型集合TA、TD；

3. 构建攻击者、防御者行动集合MA、MD；

7. 采用公式(5)计算攻击者收益；

8. 采用公式(6)计算防御者收益}

9. 调用混合策略贝叶斯均衡求解子算法MSBNE(SBGM)；

11.得到信息系统整体风险RALL。

END

算法2混合策略贝叶斯纳什均衡求解子算法MSBNE(SBGM)

输入：SBGM模型;

输出：混合策略贝叶斯纳什均衡。

1. 根据历史数据得到PA、PD；

输出：信息系统整体风险RALL。

基于静态贝叶斯博弈的风险评估算法中最为关键的步骤为SBGM模型的建立和求解，包括应对攻击策略的特定防御策略集合的建立、策略成本和收益量化及静态贝叶斯博弈模型的求解。子算法1利用非线性规划求解SBGM模型的混合策略贝叶斯纳什均衡，由于本文中静态贝叶斯博弈是非零和的，其时间复杂度O(|SA(tA)|·|SD(tD)|·|tA|·|tD|)，如表1所示；子算法2计算信息系统的整体风险，时间复杂度为O(n1·n2)。由上可知，整个算法的复杂度满足信息系统的需求。

Table 1　Method comparison

注：n、m分别为攻击者和防御者的策略数量。

信息需求(Information Requirement)是指算法所运用的场景对攻击者和防御者所拥有信息的要求。攻击者或防御者对另一方或多或少都有信息上的不确定性，相比完全信息博弈，不完全信息博弈更加贴近实际网络场景。可操作性(Operability)是指文献给出的方法或算法是否具有较强的实用性。相比文献[4,5]，本文给出了模型的应用算法，能够较好地完成信息系统安全风险的评估，具有较好的可操作性。

4应用实例与分析

为了进一步阐述本文所提出的SBGM模型及相关算法的有效性，本文通过部署有如图2所示的网络信息系统拓扑结构进行模拟实验。该拓扑结构主要由一台文件服务器、一台数据库服务器、一台邮件服务器及一台IDS入侵检测设备组成。非本地主机只能访问文件服务器和邮件服务器，系统内的文件服务器、邮件服务器可以对数据库服务器进行访问。

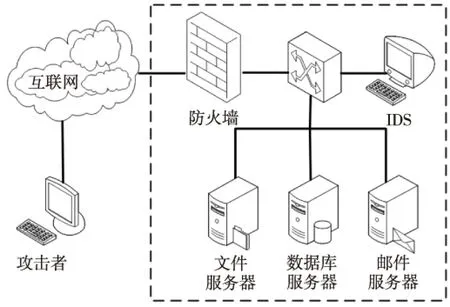
Figure 2　Network toplogical structure 图2　网络拓扑结构

防御者根据历史经验，将攻击者的类型分为tA={冒险型攻击者, 保守型攻击者}。冒险型攻击者为了达到目标不惜采用高代价攻击方式，成功率较高，具有较大风险；保守型攻击者攻击时更愿意使用代价较小的方式实施攻击，成功率较低，风险也较低。防火墙规则及服务器弱点信息如表2和表3所示。

Table 2　Firewall regulations

Table 3　Weakness of the server

假设攻击者在攻击主机上具有Root权限，并以此作为攻击的起点，以获取数据库服务器的重要信息为目标。根据防火墙的相关规则，攻击主机仅可以获得Access权限去访问邮件服务器和文件服务器，无法访问数据库服务器。但是，由于弱点间存在相互依赖关系，攻击者可以通过一系列的原子攻击来获得访问数据库的权限。攻击者的原子攻击信息如表4所示。

Table 4　Description of atom attack

对网络拓扑进行分析可得到攻击者可采取的各类攻击行动。不同类型的攻击者采取的攻击策略不同，表5给出了不同类型的攻击者所采取的行动。防御者有两种类型，从防御行为库选出可用的防御行动后，经过对成本、影响及专家建议等方面的考虑，可供选取的防御行动如表6所示。

Table 5　Different types of attacker’s actions

参与者行动集合确定后，利用策略收益量化公式对各类型的参与者行动的成本和收益进行量化。另外，通过对历史数据的分析，防御者可得到攻击者类型的先验信念：(冒险型攻击者，保守型攻击者)=(0.6, 0.4)，防御者对攻击者历史行为进行分析，可得到攻击者对其类型的先验信念：(防御等级高，防御等级低)=(0.5, 0.5)。由此可得到网络博弈树如图3所示。

Table 6　Different types of defender’s actions

Figure 3　Net game tree 图3　网络博弈树

利用最优防御策略选取算法可得到均衡如下：

Table 7　Bayesian Nash equilibrium of the mixed strategies

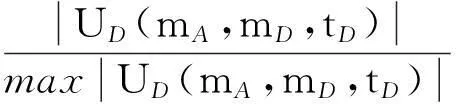
如果该信息系统包含四个安全风险子域，同理，可计算得到四个风险子域的风险为(R1,R2,R3,R4)=(0.733 65,0.629 91,0.698 33,0.563 54)。假设该信息系统各风险子域的资产值(A1,A2,A3,A4)=(100,80,130,110)(单位：万元)，则可得到安全风险子域的权重向量为(0.238 1,0.190 5,0.309 5,0.261 9)。则信息系统的整体风险RALL=0.658 4，由此认为该系统风险级别为中等。

由此可见，本文提出的方法是切实可行的，综合考虑了攻击者和防御者的行为，并运用攻击者的混合均衡策略对风险进行评估，操作简单，性能开销复杂度小。而文献[1]中的方法对大样本数据学习的速度较慢，序列训练开销大。文献[2]中的方法仅能对实时风险进行评估，且开销较大。文献[3]中的方法状态概率转移矩阵不易确定，具有较大主观因素。更为重要的是，以上文献的评估方法都仅仅站在防御方的角度对系统风险进行评估，较为片面。

5结束语

为了全面、主动地进行信息系统风险评估，本文基于静态贝叶斯博弈理论建立攻防博弈模型。根据攻防双方的不完全信息将攻击者和防御者划分为多种类型，对博弈的均衡情况进行了分析和证明。然后，对混合策略均衡进行分析，将攻击者的混合策略均衡作为防御者对攻击行动的可信预测。在此基础上，结合威胁发生给系统造成的损失，给出信息系统风险计算公式。本文还提出了基于静态贝叶斯博弈的风险评估算法，可用于对信息系统存在的总风险进行评估。实例分析说明了本文提出模型和算法在攻击预测及风险评估方面的合理性和有效性。

参考文献:

[1]LiuFang,CaiZhi-ping,XiaoYi-nong,etal.Riskprobabilityestimatingmodelbasedonneuralnetworks[J].ComputerScience, 2008,35(12):28-33.(inChinese)

[2]WangYi-feng,LiTao,HuXiao-qin,etal.Areal-timemethodofriskevaluationbasedonartificialimmunesystemfornetworksecurity[J].ACTAElectronicaSinica, 2005,33(5):945-949.(inChinese)

[3]LiuGang,LiQian-mu,LiuFeng-yu,etal.Atime-varyingMarkovmodelanditsapplicationtonetworkreal-timeriskprobabilityprediction[J].ActaArmamentarii, 2012,33(2):163-169.(inChinese)

[4]CaiJian-qiang.Networkvulnerabilityassessmentbasedongamemodel[D].Baoding:NorthChinaElectricPowerUniversity, 2011.(inChinese)

[5]ZhangShu-wei,LiuWen-fen,WeiJiang-hong.Networksecurityriskquantificationassessmentbasedongamemodel[J].JournalofInformationEngineeringUniversity, 2014,15(2):152-162.(inChinese)

[6]FudenbergD,TiroleJ.Gametheory[M].Cambridge:TheMITPress, 1991.

[7]LiuY,CristinaC,HongM.ABayesiangameapproachforintrusiondetectioninwirelessadhocnetworks[C]//Procofthe2006WorkshoponGameTheoryforCommunicationsandNetworks, 2006:1.

[8]JiangWei,FangBing-xing,TianZhi-hong,etal.Evaluatingnetworksecurityandoptimalactivedefensebasedonattack-defensegamemodel[J].ChineseJournalofComputers, 2009, 32(4):817-825.(inChinese)

[9]RobertG.Aprimeringametheory[M].NewYork:PearsonHigherEducation, 1992.

[10]MyersonJ.Bayesianequilibriumandincentivecompatibility:Anintroduction[C]//SocialGoalsandSocialOrganization,Cambridge:CambridgeUniversityPress,1985.

[11]ZhengGeng-zhong,LiuSan-yang,QiXiao-gang.ClusteringroutingalgorithmofwirelesssensornetworksbasedonBayesiangame[J].JournalofSystemsEngineeringandElectronics, 2012, 23(1):154-159.

[12]ChenX,DengX.Settlingthecomplexityoftwo-playerNashequilibrium[C]//Procofthe47thAnnualIEEESymposiumonFoundationsofComputerScience(FOCS06),2006:261-272.

参考文献附中文.

[1]刘芳，蔡志平，肖依,等．基于神经网络的安全风险概率预测模型[J]．计算机科学，2008,35(12):28-33.

[2]王益丰，李涛，胡晓勤,等．一种基于人工免疫的网络安全实时风险检测方法[J]．电子学报,2005,33(5):945-949.

[3]刘刚，李千目，刘凤玉,等. 面向网络实时风险预测的马尔可夫时变模型[J]. 兵工学报, 2012,33(2):163-169.

[4]蔡建强. 基于博弈模型的网络脆弱性评估的研究[D]. 保定:华北电力大学, 2011.

[5]张树伟, 刘文芬, 魏江宏. 基于博弈模型的网络风险量化评估方法[J]. 信息工程大学学报, 2014,15(2):156-162.

[8]姜伟, 方滨兴, 田志宏,等.基于攻防博弈模型的网络安全测评和最优主动防御[J].计算机学报，2009，32(4):817-825.

余定坤(1991-),男,江西赣州人，硕士生，研究方向为风险评估和信息安全。E-mail:78729557@qq.com

YUDing-kun,bornin1991,MScandidate,hisresearchinterestsincluderiskassessment,andinformationsecurity.

王晋东(1966-),男,山西洪洞人，教授，研究方向为资源管理和风险评估。E-mail:wjd9797@sina.com

WANGJin-dong,bornin1966,professor,hisresearchinterestsincluderesourcesmanagement,andriskassessment.

张恒巍(1977-),男,河南洛阳人，博士生，讲师，研究方向为风险测评、风险评估和博弈论。E-mail:zhw11qd@126.com

ZHANGHeng-wei,bornin1977,PhDcandidate,lecturer,hisresearchinterestsincluderiskevaluation,riskassessment,andgametheory.

王娜(1970-),女,河北安平人，硕士，副教授，研究方向为资源管理和物联网。E-mail:wang_na70@sohu.com

WANGNa,bornin1970,MS,associateprofessor,herresearchinterestsincluderesourcesmanagement,andtheInternetofThings.

陈宇(1977-),男,河南邓州人，博士生，讲师，研究方向为风险评估和物联网。E-mail:chenyu0319@gmail.com

CHENYu,bornin1977,PhDcandidate,lecturer,hisresearchinterestsincluderiskassessment,andtheInternetofThings.