求解互补支持向量机的非单调信赖域算法

求解互补支持向量机的非单调信赖域算法*

高雷阜，于冬梅，赵世杰

(辽宁工程技术大学优化与决策研究所，辽宁 阜新 123000)

摘要：求解支持向量机的核心问题是对一个大规模凸二次规划问题进行求解。基于支持向量机的修正模型，得到一个与之等价的互补问题，利用Fischer-Burmeister互补函数，从一个新的角度提出了求解互补支持向量机的非单调信赖域算法。新算法避免了求解Hesse矩阵或矩阵求逆运算，减少了工作量，提高了运算效率。在不需要任何假设的情况下，证明算法具有全局收敛性。数值实验结果表明，对于大规模非线性分类问题，该算法的运行速度比LSVM算法和下降法快，为求解SVM优化问题提供了一种新的可行方法。

关键词：支持向量机；信赖域方法；互补函数；非单调策略

中图分类号：TP301.6 文献标志码：A

doi:10.3969/j.issn.1007-130X.2015.06.016

收稿日期：*2014-04-14;修回日期：2014-08-11

基金项目：教育部高校博士学科科研基金联合资助项目(20132121110009)

作者简介:

通信地址：123000 辽宁省阜新市辽宁工程技术大学理学院

Address:College of Science,Liaoning Technical University,Fuxin 123000,Liaoning,P.R.China

A non-monotonic trust region algorithm for solving complementary support vector machine

GAO Lei-fu,YU Dong-mei,ZHAO Shi-jie

(Research Institute of Optimization and Decision,Liaoning Technical University,Fuxin 123000,China)

Abstract:Solving a large-scale convex quadratic programming problem is the core of the support vector machine. An equivalence complementarity problem can be obtained based on an amended model of the surpport vector machine(SVM), therefore we propose a non-monotonic trust region algorithm for solving the complementarity problem based on the Fischer-Burmeister complementarity function. The new algorithm need not compute any Hesse or the inverse matrix, thus reducing the amount of computational work. Global convergence of the algorithm is proved without any assumptions. Numerical experiments show that the running speed of the algorithm is faster than that of the LSVM algorithm and the descent algorithm when solving large-scale nonlinear classification problems and thus it provides a feasible method for solving SVM.

Key words:support vector machine；trust-region method；complementarity function；non-monotonic strategies

1引言

支持向量机SVM(Support Vector Machine)是由Vapnik V[1,2]基于统计学理论中的结构风险极小化原则提出的，它是一种有监督的机器学习，是模式识别中分类、函数近似和回归估计的有效工具。在二分类问题模型中，支持向量机模型采用结构风险极小化原则和核函数方法来构造分类模型，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并推广应用到函数拟合等其他研究领域中，例如图像处理[3]、信用风险评估[4]、股指期货预测[5]等方面的应用。SVM模型采用极大间隔的方法和结构风险最小化原则对分类函数进行学习，其模型是一个二次规划QP(Quadratic Programming)问题，随着数据规模的增大，模型的求解变得越来越复杂。因此，寻求可行的算法成为人们研究的热点。常用求解算法的思想是通过一系列子二次规划问题的求解得到原问题的解，如块算法、分解算法和增量算法等[6]，这些算法在一定程度上节省了计算机内存，提高了计算效率，但算法的设计和实现比较复杂。对于大规模非线性分类问题，Mangasarian O L 等人[7]对SVM模型进行优化，提出了Lagrangian支持向量机(LSVM)模型，并提出了LSVM算法。但是，算法中仍然存在矩阵的求逆运算，特别是对于非线性的高维数据，高阶矩阵的求逆运算直接影响了算法的训练速度。

针对LSVM的缺陷，张襄松等人[8]提出互补支持向量机的下降算法，但下降法不稳定，对微小扰动敏感。为了克服LSVM算法和下降算法的缺陷，本文提出了求解互补支持向量机的非单调信赖域方法，并给出了算法的具体实现过程和算法的收敛性证明。最后，通过数值实验验证了算法的可行性和有效性。

2问题的提出

假设训练:

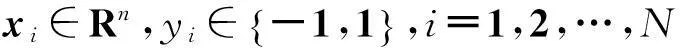
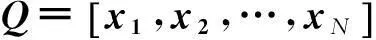
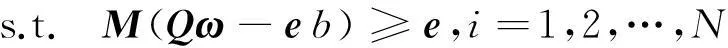
(1)

其中，参数e=(1,1,…,1)T。

对二次规划问题(1)，通常转化为它的对偶问题[9]求解：

(2)

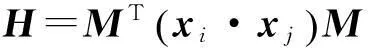
利用式(2)的KKT(Karush-Kuhn-Tucker)充要条件及互补问题的等价形式，可以得到式(2)的等价形式[9]：

(3)

MangasarianOL等人给出了式(3)的等价形式:

(4)

并利用:

(5)

提出了一个简单的迭代算法(LSVM算法)。该算法中存在求逆矩阵的运算，对线性分类问题可以使用等式Sherman-Morrison-Wood-bury(SMW)来计算矩阵，从而提高运算效率。但是，对于非线性分类问题，高阶矩阵的求逆运算直接影响了算法的训练速度，因此该方法只适用于求解中小规模非线性分类问题。

3问题的转化

求解支持向量机的二次规划问题等价于求解一个互补问题(3)。因此，本文基于Fischer-Burmeister[10]互补函数，并且该函数可以推广到矩阵域中[10]，将其转化为一个无约束最优化问题进行求解。

定义1对∀a,b∈R2，映射Ψ:R2→R，如果该映射Ψ满足

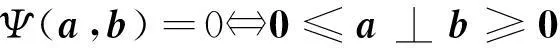
(6)

则映射Ψ为一个互补函数。

定义2

(7)

对∀λ∈RN，令q(λ)=Hλ-e，则由互补函数可将式(3)转化为如下方程组:

(8)

上式等价于求解无约束最优化问题:

(9)

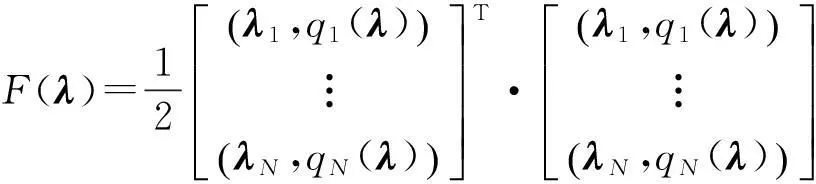
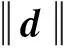
(10)

令Fk=F(λk),记dk是问题(10)式的解，令目标函数的预估下降量为:

(11)

目标函数的真实下降量为:

则真实下降量与预估下降量的比值rk为:

(12)

信赖域算法求解时若rk≥c，其中c∈(0,1)，则接受dk，λk+1=λk+dk，信赖域半径增加或者不变；否则信赖域半径减少，求新的dk和rk。重复以上过程即可求得无约束优化问题的最优解。下面引入非单调自适应策略，令迭代过程中gk=▽F(λk)，Gk=dT▽F(λk)▽F(λk)Td，Gk为正定矩阵。

定义3

(13)

其中，l(k)=min{t(k-1)+1,T}，T是非负整数，t(0)=0。

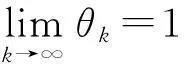
引入参数θk的目的是，如果选取的搜索点恰好处于峡谷附近，那么，它在搜索时就会沿着峡谷缓慢前进，在搜索时出现锯齿现象，搜索到的最优解很可能是局部最优解。通过引入一个参数，使得信赖域半径的校正条件适当放宽，进而跳出峡谷，搜索到全局最优解。

则接受λk+1=λk+dk。

4非单调信赖域算法求解二次规划问题

以下给出非单调信赖域算法的具体实现过程：

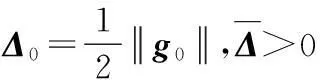
步骤3求解无约束优化问题的信赖域子问题式(10)，利用式(12)得到求Fl(k)。

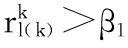
步骤5校正信赖域半径:

步骤6修正gk+1，k=k+1，转步骤2。

5算法收敛性分析

引理1设dk是信赖域子问题(10)的解，则必有：

(14)

最早关于不等式(14)的证明由PowellMJD[12]给出，对于上式的详细证明见文献[12]。

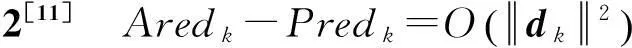
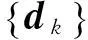
证明假设上述结论不成立，即算法中步骤2到步骤4间的内循环不在有限步终止。令Si是在dk处第i次的内循环，故rk(i)≤c0,i=1,2,…，且当i→∞时，Δk(0)→0。

由引理1和引理2可知:

□

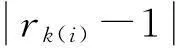
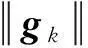
(15)

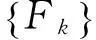
(16)

可以证明对任意k都有：

(17)

当k→∞时，有：

由式(17)可知，当k充分大时，

□

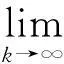
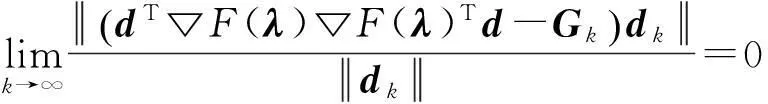
证明由假设条件可以得到：

其中，γ为常数[15～17]。

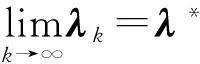
由于B(λ)是非奇异的，则存在ε>0，k0>0，对∀k>k0都有:

故，

又由于

□

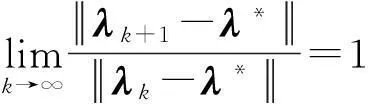
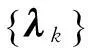
6数值实验

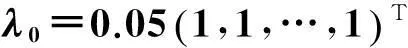
经过对实验数据进行剔除异常值和通过数据拟合确定缺失值，以及去量纲、归一化处理操作后得到待分析数据集。分别采用LSVM算法[7]、下降法[8]和本文中的非单调信赖域算法将随机选择的数据集作为实验数据进行实验，三种方法分类性能比较见表1。同时，在同样的参数设置情况下，随机选择两个数据集Balance Scale和Statlog作为实验数据，得到如图1和图2所示的分类正确率情况比较。文中SVM的核函数选用的是径向基核函数。

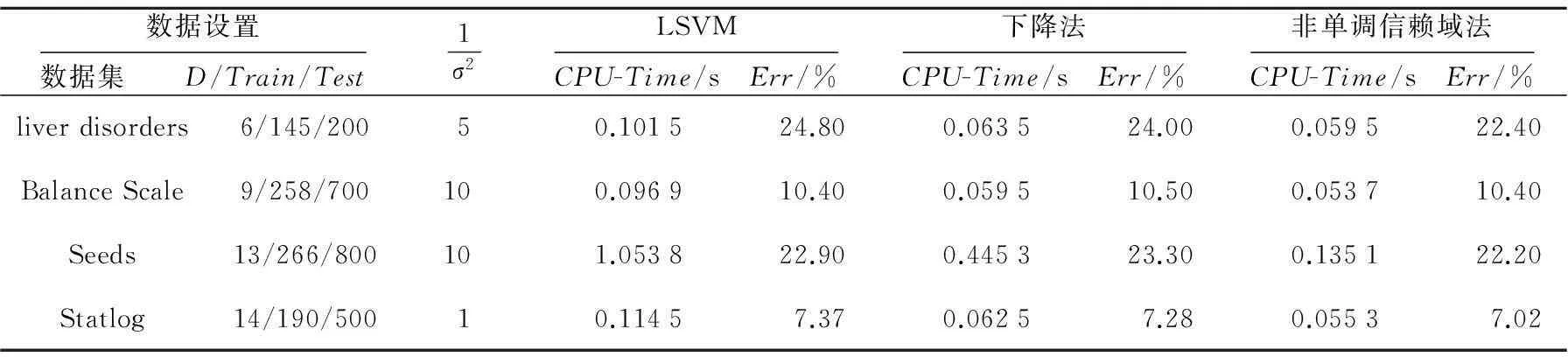
Table 1　Comparison of the numerical results of the three algorithms

表1中字母D表示相应实际数据集的属性数目；Train表示SVM训练数据个数；Test表示SVM测试数据个数；CPU-Time表示相应算法的CPU运行时间，单位为s；Err%表示算法对应的测试数据的错分率。

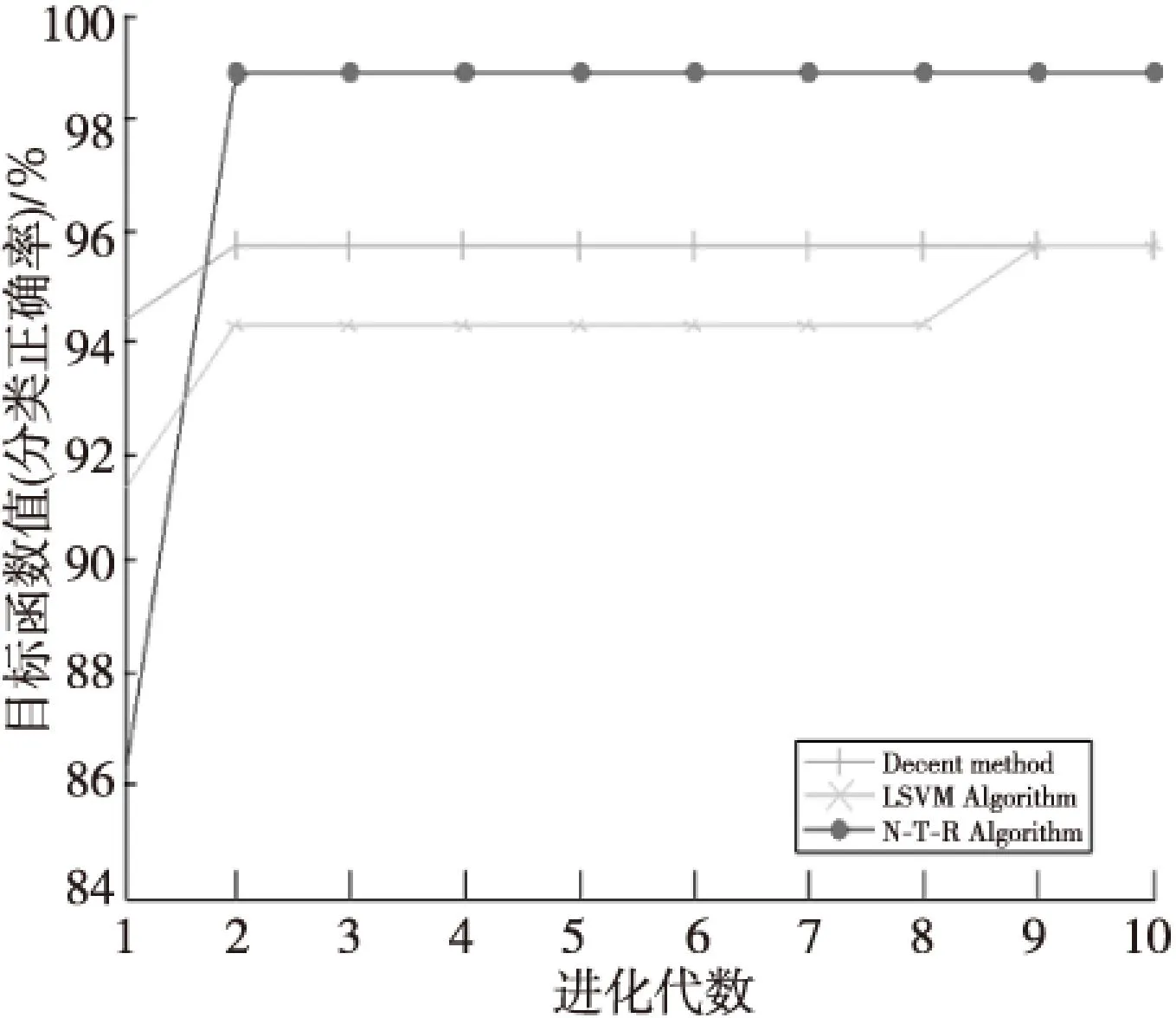
Figure 1　Comparson results of the three algorithms on liver disorders data sets 图1　三种算法在数据集liver disorders上的对比结果

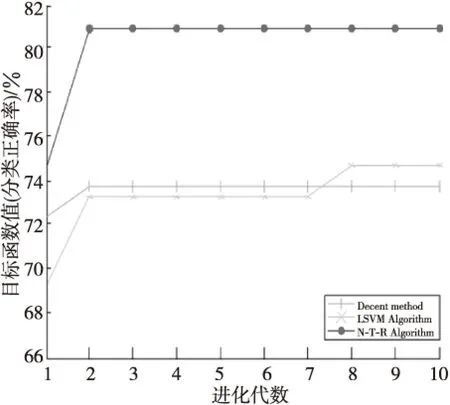
Figure 2　Comparison results of the three algorithms on Statlog data sets 图2　三种算法在数据集Statlog上的对比结果

由表1实验结果可以看出，在数据集规模增大时，非单调信赖域算法的运行时间并未明显增加，并保持相当的数据错分率。在数据错分率相当的情况下，非单调信赖域算法的CPU运行时间较短，显现出了较好的优势，且训练正确率相当，甚至更好。随机选择两个数据集Balance Scale和Statlog作为实验数据，通过图1和图2可以看出，非单调信赖域算法(N-T-R Algorithm)与LSVM算法(LSVM Algorithm)和下降法(Decent method)相比，非单调信赖域算法提高了支持向量机的分类正确率，说明非单调信赖域算法对于求解互补支持向量机模型是可行的。

7结束语

本文基于互补支持向量机问题，利用Fischer-Burmeister互补函数将其转化为无约束优化问题并构造该问题的信赖域子问题，给出了求解互补支持向量机的非单调信赖域算法。新算法通过修正信赖域半径的校正条件和自适应调整信赖域半径搜索最优解，克服了在求解大规模非线性分类问题时需要计算Hesse矩阵及矩阵求逆运算的缺陷，算法过程简单，易于实现并具有线性收敛性。数值实验结果表明，非单调信赖域算法求解互补支持向量机比LSVM算法和下降点算法优越。将半定规划与互补支持向量机问题融合将是今后的研究重点。

参考文献:

[1]Cortes C, Vapnik V.Support-Vector Networks[J]. Machine Learning,1995,20,273-297.

[2]Vapnik V. The nature of statistical learning theory[M].New York:Springer,1998.

[3]Wu Peng,Song Wen-long.An improved SVM-based image edge detection method[J]. Pattern Recognition and Simulation,2012,31(4):65-68.(in Chinese)

[4]Yao Xiao,Yu Le-an.A fuzzy proximal support vector machine model and its application to credit risk analysis[J]. Systems Engineering-Theory & Practice,2012,32(3):549-554.(in Chinese)

[5]Sai Ying,Zhang Feng-ting,Zhang Tao. Research of Chinese stock index futures regression prediction based on support vector machines[J].Chinese Journal of Management of Science,2013,21(3):35-39.(in Chinese)

[6]Ding Shi-fei, Qi Bing-juan, Tan Hong-yan. An overview on theory and algorithm of support vector machines[J]. Journal of University of Electronic Science and Technology of China,2011,40 (1):2-10.(in Chinese)

[7]Mangasarian O L,Musicant D R.Lagrangian support vector machines[J].Journal of Machine Learning Research,2001,3(1):161-177.

[8]Zhang Yang-song, Liu San-yang.Complementarity support vector machines[J].Computer Science,2010,37 (2):165-166.(in Chinese)

[9]Mangasarian O L.Successive over relaxation for support vector machines[J].IEEE Transactions on Neural Networks,1999,10(5):1032-1037.

[10]Fischer A.A special newton-type optimization methods[J].Optimization:A Journal of Mathematical Programming and Operations Research, 1992,24(3):269-284.

[11]Yuan Ya-xiang,Sun Wen-yu. Optimazation theory and method[M].Beijing:Science Press,1997.(in Chinese)

[12]Powell M J D,Yuan Y.A trust region algorithm for equality constrained optimization[J]. Mathematical Programming,1990,49(3):189-211.

[13]Fu J H,Sun W.Nonmonotone adaptive trust-region method for unconstrained optimization problems[J].Applied Mathematics and Compuation,2005,163(5):489-504.

[14]Wang Jian-ping,Lv Yi-bin,Zhang Xiao-peng.A new nonmonotone trust region algorithm of unconstrained optimization[J]. Science Technology and Engineering,2012,12(14):3291-3294.(in Chinese)

[15]Chua C B,Yi P.A continuation method for nonlinear complementarity problems over symmetric cones[J]. SIAM Journal on Optimization,2010,20(5):2560-2583.

[16]Fang L,He G P,Hu Y H. A new smoothing Newton-type method for second-order cone programming problems[J].Applied Mathematics and Computation,2009,215.1020-1029.

[17]Li Gai-di. A trust region method with automatic determination of the trust region radius[J].Journal of Engineering Mathematics,2006,23(5):843-848.(in Chinese)

参考文献：附中文

[3]吴鹏,宋文龙.一种改善的基于支持向量机的图像边缘检测算法[J].模式识别与仿真,2012,31(4):65-68.

[4]姚潇,余乐安.模糊近似支持向量机模型及其在信用风险评估中的应用[J].系统工程理论与实践,2012,32(3):549-554.

[5]赛英,张凤廷,张涛. 基于支持向量机的中国股指期货回归预测研究[J].中国管理科学,2013,21(3):35-39.

[6]丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):2-10.

[8]张襄松,刘三阳.互补支持向量机[J].计算机科学,2010,37(2):165-166.

[11]袁亚湘,孙文瑜.最优化理论与方法[M].北京：科学出版社,1997.

[14]王剑平,吕毅斌,张晓鹏.无约束优化的一类新的非单调信赖域算法[J].科学技术与工程,2012,12(14):3291-3294.

[17]李改弟. 一个自动确定信赖域半径的信赖域方法[J].工程数学学报,2006,23(5):843-848.

高雷阜(1963-),男,辽宁阜新人，博士，教授，研究方向为最优化理论与应用和非线性动力系统预测。E-mail:gaoleifu-@163.com

GAO Lei-fu,born in 1963,PhD,professor,his research interests include optimization theory and application，and nonlinear dynamic system prediction.

于冬梅(1986-),女,辽宁鞍山人，博士生，研究方向为最优化理论与应用和锥优化。E-mail:yudongmei1113@163.com

YU Dong-mei,born in 1986,PhD candidate,his research interests include optimization theory and application,and cone optimization.

赵世杰(1987-),男,山东五莲人，博士生，研究方向为最优化理论与应用。E-mail:zhao2008shijie@126.com

ZHAO Shi-jie,born in 1987,PhD candidate,his research interests include optimization theory and application.