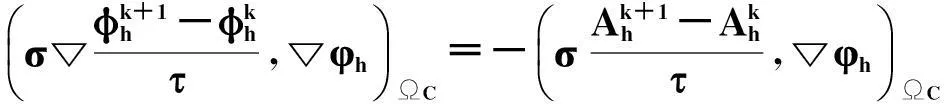带有非线性边界条件涡流方程的A-φ有限元算法

张立成，王然，晋斌，王斌

(中国传媒大学 理工学部，北京 100024)

带有非线性边界条件涡流方程的A-φ有限元算法

张立成，王然，晋斌，王斌

(中国传媒大学 理工学部，北京 100024)

摘要：利用A-φ方法对带有非线性边界条件的涡流方程提出了耦合和解耦两种有限元算法。非线性项表现为指数形式：H×n=n×|E×n|α-1E×nα∈(0，1]。在每一个计算步骤里，耦合算法在一个方程里面同时求解矢量A和标量φ，而解耦算法在两个不同的方程里面分别求解矢量A和标量φ；再通过一些数值实验来对两种算法的可行性、收敛性等进行对比。

关键词：涡流方程；非线性边界；有限元；A-φ耦合解耦算法

中图分类号：O212.4

文献标识码：：A

文章编号：：1673-4793(2015)01-0057-05

Abstract：We use A-φ method to suggest a coupled and a decoupled fully discrete numerical scheme to solve eddy current equations with nonlinear boundary condition obedient to a power-law formH×n=n×|E×n|α-1E×nα∈(0，1]. At every time step，the coupled scheme is to solve A and φ in one equation at the same time，and the decoupled scheme needs to solve two separate equation for the A and the φ respectively. And we present some numerical experiments to compare the two schemes.

Keywords：eddy current equations；nonlinear boundary condition；finit element；A-φ coupled and decoupled scheme

收稿日期：2014-12-15

作者简介：张立成(1985-)，男(汉族)，天津人，中国传媒大学硕士研究生.E-mail：darlyz@163.com

A-φFinite Element Scheme for Eddy Current Equations

with Nonlinear Boundary Condition

ZHANG Li-cheng，WANG Ran，JIN Bin，WANG Bin

(Science School，Communication University of China，Beijing 100024，China)

1A-φ有限元耦合和解耦算法的提出

(1)

H×n=n×g(E×n)=n×(|E×n|α-1E×n)α∈(0，1] 在Г上。

(2)

(3)

其中其中[·]代表ГC上的跳跃，φ0和散度自由的A0满足分解式E0=A0+▽φ0。我们定义Hm()：={v∈L2()，Dξv∈L2()，0<|ξ|≤m}，其中ξ为非负多重指数，且用粗体来表示矢量纲，如L2()：=(L2())3。另外，令Ls(Г)(s>1)记为Г上的s可积空间，且L2内积定义为(u，v)Г=∫Гu·v。然后我们定义Hilbert空间()：={v∈H1()，v·n=0onГ}。我们令Γh是的网格尺寸为h标准四面体单元划分，其子区域C和E划分的并集，其中表示C的网格划分。于是我们定义

Wh={φ∈H1(C)∩C(C)，φ|K∈ρ1，∀，

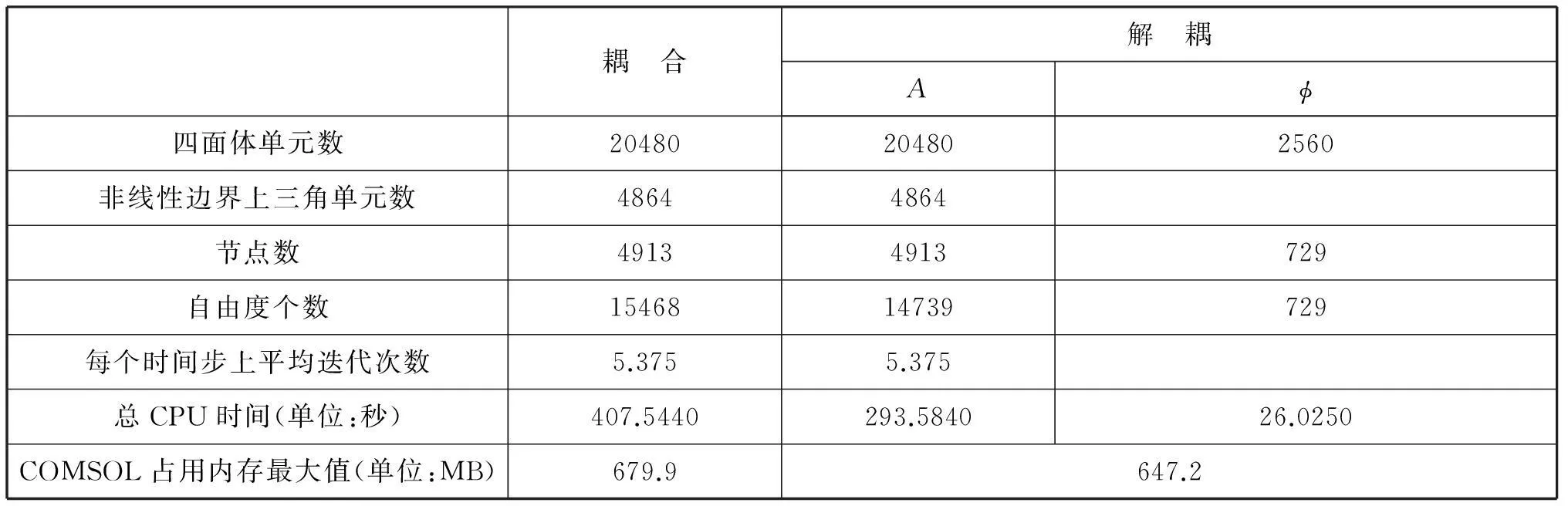
通过时间节点0=t0

1.1　耦合求解算法

2.2　解耦求解算法

两种算法解的适定性均可由强制性和非线性算子单调性证得，并可求得收敛阶为0(τ+hα)。

2数值实验

实验1：我们选取空间线性的真解：

t∈[0，1]。分解电场Eex为

与φex(x，t)=(sin(πt)+1)(x+y+z+1)。显然误差与网格尺寸无关，我们用粗网格计算α=0.1和α=0.4情况下两种算法的误差，结果如图1所示，log2err的函数图像按log2τ描绘。对于两种算法来说，不同的α得到了几乎相同的收敛率，且均比理论值0(τ)要好。

(a)耦合格式收敛曲线，平均斜率为1.626　　　　　　(b)解耦格式收敛曲线，平均斜率为1.776图1　空间线性的真解对于不同的解耦算法所得的收敛曲线

实验2：第二个实验我们选取真解：

(a)耦合算法(α=0.1)　　　　　(b) 解耦算法(α=0.1)

(c)耦合算法(α=0.4)　　　　　(d) 解耦算法(α=0.4)图2　实验2不同的求解算法在α分别取0.1和0.4时所得的收敛曲线

我们将实验2中α=0.1且h=1/16 两种算法的误差曲线进行比较(如图3)，可以观察到随着时间步长的不断减小两种算法收敛于同一值，而时间步长较大时解耦算法比耦合算法的误差稍大。α和h取其他值时同样如此，这里不再一一展示。

图3

最后我们在CPU：intel corl2 2.2GHz，RAM：4GB，win8x64机器中记录了实验2中当，τ=1/32，h=1/16且α=0.1时两种求解算法计算时所需资源如表1所示。

表1

耦 合解 耦Aϕ四面体单元数20480204802560非线性边界上三角单元数48644864节点数49134913729自由度个数1546814739729每个时间步上平均迭代次数5.3755.375总CPU时间(单位:秒)407.5440293.584026.0250COMSOL占用内存最大值(单位:MB)679.9647.2

3总结

本文我们提出了对带有非线性边界条件的涡流方程基于A-φ分解的耦合和解耦两种有限元算法，并对两种算法的收敛效果进行了数值实验对比。我们发现整体收敛性上，两种算法的结果是类似的。以时间步长上来看，时间步长较大时耦合算法比解耦算法的误差要小，但是随着时间步长的减小，则收敛于同样的值，其取决于空间网格尺度的误差。但是在相同计算资源的配置下，所用时间和内存，解耦算法要均小于耦合算法。

参考文献：

[1]Slodicˇka M，Zemanová V. Time-discretization scheme for quasi-static Maxwell’s equations with a non-linear boundary condition[J].J Comput Appl Math，2008， 216：514-522.

[2]Vrábel V，Slodicˇka M. An eddy current problem with a nonlinear evolution boundary condition[J].J Math Anal Appl，2012，387：267-283.

[3]Kang T，Chen T，Zhang H，Kim K I. Fully discrete A-φ finite element method for Maxwell’s equations with nonlinear conductivity[J].Numer Meth Part D E，2014，30：2083-2108.

[4]Kang T，Kim K I. Fully discrete potential-based finite element methods for a transient eddy current problem[J].Computing，2009，85：339-362.

[5]Susanne C Brenner，Ridgway Scott L. The Mathematical Theory of Finite Element Methods(Second Edition)[M].NY：Springer，2007：60-62.

[6]胡建伟，汤怀民.微分方程数值方法 (第二版)[M].北京：科学出版社，2011.

(责任编辑：王谦)