基于代理重加密技术的网络编码安全算法研究

方驰，潘耘

(中国传媒大学 计算机学院，北京 100024)

基于代理重加密技术的网络编码安全算法研究

方驰，潘耘

(中国传媒大学 计算机学院，北京 100024)

摘要：介绍了网络编码安全性的相关研究，着重介绍了代理重加密技术与同态加密技术，并基于代理重加密技术提出了新型的防窃听网络编码算法，保证了编码数据的机密性和完整性。同时给出了在单源单宿、多源多宿、单源多宿、多源多宿情况下的加密解密步骤，有效保证了网络编码的安全性。

关键词：网络编码；代理重加密；同态加密；安全性

中图分类号：TP393.1

文献标识码：：A

文章编号：：1673-4793(2015)01-0045-06

Abstract：Network coding security related research has been introduced in this paper. PRC(Proxy Re-Cryptography) and HES(Homomorphic Encryption Schemes) will be elaborated. We will raise a new anti-eavesdrop newwork coding algorithm based on PRC and HES. This can ensure the security and integrity of the coding date.At the same time，we will explain the steps of encryptin and decryption in some situations to confirm the security of network coding.

Keywords：network coding；proxy re-cryptography；homomorphic encryption；security

收稿日期：2014-12-16

作者简介：方驰(1990-)，男(汉族)，安徽芜湖人，中国传媒大学计算机学院研究生.E-mail：356168330@qq.com

A Security Network Coding Algorithm Based

on Proxy Re-Cryptography

FANG Chi，PAN Yun

( Computer Science School，Communication University of China，Beijing 100024，China)

1引言

与基于传统路由的网络安全防护相比，网络编码节点对信息的编码融合使得网络编码环境下的网络攻击行为更具多样性和隐蔽性，因而对这些攻击的感知与防范也更具挑战性。当前，关于网络编码安全机制的研究尚处于零散研究阶段。首先，目前主要关注的是在如何防止窃听和抑制污染攻击，即关于编码数据的机密性和完整性的研究，而对于其它安全属性与隐私保护的研究还尚未展开。其次，所采用的技术手段也还很有限，主要是基于信息论的方法、融合纠错与网络编码的方法、以及密码学中的同态哈希和同态签名技术。而近年来已经取得快速进展的同态加密技术和代理重加密技术等均尚未在安全网络编码领域得到有效应用。一种比较通用的分类方法是将安全网络编码研究所涉及到的主要安全威胁归为两大类，即窃听攻击和污染攻击。最近，也有学者提出了针对网络编码的熵攻击。这些攻击分别威胁到相关编码数据的机密性、完整性和可用性。

2相关研究

窃听攻击(也称被动攻击)是指攻击者通过搭线窃听的方式获取不该让其知道的内容，这种攻击破坏的是网络编码的机密性。2002年，蔡宁和杨伟豪[1]最先研究了无环网络中数据安全组播问题，给出了针对网络编码的窃听攻击模型，针对能窃听网络中一定数量信道的窃听者设计了一种信息论安全的网络编码并且给出了具体的编码方法，拉开了网络编码安全机制研究的序幕。之后，Feldman等人(2004)[2]也考虑了此类问题，在蔡-杨的基础上证明：将线性网络编码变为安全网络编码等价于求解满足一定广义距离性质的线性码，并说明可以通过舍弃少量带宽而给出在较小有限域上的安全网络编码。2004-2005年期间，Jain等人[3，4]将蔡-杨的安全网络编码模型推广到无线网络中，并得到了单源 (有环或无环) 网络中以单位速率安全单播的充要条件。 信息论安全的网络编码模型存在的一个主要问题是：当利用随机网络编码时，编码安全的概率非常低；要想达到安全的要求，编码系数都要特别选取。Tan等人(2006年)[5]对编码系数选取的代价进行了分析，Silva等人(2008年)[6，7]用Rank-Metric的方法给出了此类问题的一个解决方案；Rouayheb等人(2007~2009年)[8，9]也针对此类问题展开了系统的研究，并给出了有效的编码系数选择方法。另外一条防窃听攻击的研究思路是所谓的弱安全网络编码模型，它是由Bhattad和Narayanan等人(2005)[10]研究无环组播网络编码的安全问题时提出的，它与蔡-杨网络编码安全模型的差别在于：前者的安全目标是要求窃听者得不到有关信源发出的任何部分消息，而后者的安全目标是要求窃听者得不到由任何信源发出的所有消息。 他们证明：当窃听者窃听到的信道数小于网络的最大流时，窃听者得不到关于信源任何有意义的信息；而且，在弱安全的条件下可以达到网络的最大流。但是，其编码体制的缺点是应用随机网络编码时不能以概率1达到弱安全的要求。Silva等人(2009)[11]针对此问题给出了一种通用弱安全网络编码体制，该体制利用代数编码技巧，使得随机网络编码能以概率1达到弱安全的要求。此外，蔡宁和杨伟豪(2007)[12]在分析多信源线性网络编码代数结构的基础上，给出了弱安全网络编码模型安全传输的充分必要条件，该条件表明此类网络上的网络编码的安全性依赖于信源分布。2008年，Chan等人[13]进一步推广了蔡宁和杨伟豪所得到的相关结论，讨论了多信源安全网络通信问题，在一定的窃听范围的限制下，利用随机网络编码的方法，给出了多信源安全网络编码容量的内界、外界和线性规划界。

信息论安全的网络编码追求的是一种无条件安全，即跟攻击者计算能力无关。现有防窃听网络编码算法为达到信息论安全往往要求牺牲较多带宽。然而，现实通信环境中的攻击者的计算能力总可以被认为是有限的。因此，可以研究所谓的计算性安全的网络编码。

3代理重密码与同态加密技术

3.1　代理重密码技术

代理重密码(Proxy Re-Cryptography，PRC)原语包括代理重加密(Proxy Re-Encryption，PRE)原语和代理重签名(Proxy Re-Signature，PRS)原语。PRE和PRS近年来在理论和应用两方面的研究进展都非常迅速。然而，它们在网络编码安全性方面的应用还是个空白。因此，本项目拟围绕PRC在网络编码安全方面的应用展开研究，具体拟解决如下三个关键问题：

代理重加密是密文间的一种密钥转换机制，是由Blaze 等人在1998 年的欧洲密码学年会上提出的[14]，并由Ateniese 等人在2005 年的网络和分布式系统安全研讨会议(NDSS，Network & Distributed System Security Symposium)和2007 年的美国计算机学会计算机与通信安全会议(ACMCCS，ACM Conference On Computer And Communications Security) 上给出了规范的形式化定义。在代理重加密中，一个半可信代理人(Proxy) 通过代理授权人(Delegator)产生的转换密钥Rk 把用授权人(Delegator)Alice 的公钥Pa加密的密文转化为用被授权人(Delegatee)Bob 的公钥Pb 加密的密文，在这个过程中，代理人得不到数据的明文信息，从而降低了数据泄露风险。而这两个密文所对应的明文是一样的，使Alice 和Bob 之间实现了数据共享。所谓的半可信，指的是只需相信这个代理者Proxy 一定会按方案来进行密文的转换。根据密文转换次数，代理重加密可以分为单跳(Single-hop) 代理重加密和多跳(Multi-hop) 代理重加密，单跳代理重加密只允许密文被转换一次，多跳代理重加密则允许密文被转换多次。根据密文转换方向，代理重加密也可以分为双向(Bidirectiollal) 代理重加密和单向(Unidirectiollal) 代理重加密。双向代理重加密是指代理者既可以将Alice 的密文转换成Bob 的密文，也可以将Bob的密文转换成Alice 的密文。单向代理重加密指代理者只能将Alice 的密文转换成Bob 的密文。当然，任何单向代理重加密方案都可以很容易地变成双向代理重加密方案。Blaze 等在文献[14]中提出的代理重加密方案是双向代理重加密，但上述这些方案只满足选择明文攻击(CPA，Chosen Plaintext Attacks) 安全，而实际应用通常要求密码组件能够抵抗选择密文攻击(CCA，Chosen Ciphertext Attacks) 安全。在2008 年的公钥密码学会议(PKC，Public Key Cryptography) 上，Libert 等人提出了一个无需借助随机预言机的单向代理重加密方案，该方案可以在非自适应攻陷模型下达到选择密文安全[15]。

代理重加密可以有效地解决许多应用领域中的相应问题，在加密电子邮件转发、垃圾邮件过滤、分布式文件系统的安全管理等场景中已经得到了广泛应用，如图1所示，是实际应用中一个基于代理重加密的文档跨域分发模型。

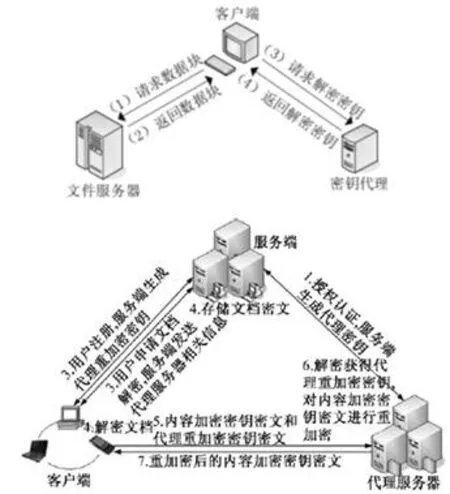
图1　基于代理重加密的文档跨域分发模型

一般来说，代理重密码包括两个部分，一个是代理重签名，一个是代理重加密"在代理重签名中，一个拥有一些额外信息的半可信代理者可以把Alice的签名转换为Bob的对同一个消息的签名，同时，这个代理者不能自己产生Alice或Bob的任何一个签名。而在代理重加密中，一个拥有一些额外信息的半可信代理者可以把用Ahce的公钥加密的密文转换为用Bob的公钥对同一个明文加密的密文，同时，这个代理者不能获得任何用Alice(Bob)的公钥加密的密文所对应明文的任何信息。

另外，代理重密码一般可以有两种分类方法一类是根据转换的方向，有单向和双向两类。前一类是只能从Alice转化到Bob，而后一类是既能从Alice转换到Bob，也能从Bob转换到Alice。另一种分类是根据转换的次数，有单用和多用两类。前一类是只能从Alice转换到Bob一次，而后一类是可以从Alice转换到Bob然后又转换到Charlie等等。

3.2　同态加密技术

Sander 和 Tschudin定义了整数范围上的加法、乘法同态加密机制，加法、乘法同态确保 2 个变量加密后的计算结果与加密前的计算结果相同。下面给出一类 HES(Homomorphic Encryption Schemes) 的简单描述：

设 R，S是 2个环，R 表示明文空间，S表示密文空间，给出如下定义 E：R→S。

(1)加法同态：如果从 E(x)和 E(y)通过加法计算可以计算出E(x+y)，则不需要知道 x，y 的值。

(2)乘法同态：如果从 E(x)和 E(y)通过乘法计算可以计算出E(x*y)，则不需要知道 x，y的值。

上述的 HES 仅仅有 2种操作：加法和乘法。需要指出的是：明文 x和密文 E(x)之间是一个一对多的关系，即：对明文x，虽然E1(x)≠E2(x)，但D(E1(x))=D(E2(x))。

由于整数范围上普通的加法和乘法都同态，因此整数范围上的同态加密就显得非常简单。设R(明文空间)和S(密文空间)为整数集，a，b∈R，E是R→S上的加密函数。如果存在算法PLUS和MULT，使其满足：

E(a+b)=PLUS(E(a)，E(b))

E(a×b)=MULT(E(a)，E(b))

这样可以利用E(a)和E(b)的值计算E(a+b)，而不需要知道 a，b 的值。称其分别满足加法同态和乘法同态。

4基于代理重加密技术的防窃听网络编码算法研究

在传统的端到端通信中，防止窃听最有效的办法就是加密。然而，尽管同态哈希、同态签名技术已经在网络编码中有较多应用，但是同态加密(Homomorphic Encryption，HE)技术在网络编码环境中的应用还非常少。出现这种情况的原因除了效率因素之外，更核心的难题在于：对于具有多个源节点和多个目的节点的网络编码结构，各个源节点不知道该用谁的公钥进行加密才能既不影响各个接收端的正确解密、又能支持中间节点对密文进行同态编码混合。因为目前已有的HE算法都只是允许把同一个接收用户的密文进行同态变换，因此不能用于多源多宿的网络编码结构。基于对PRE和HE共同的研究积累，本项目将结合二者特性，为解决这一难题提出具体的方案。既能防止窃听又允许对密文实施编码混合变换的加密体制是同态加密算法(HE)。然而，现有的HE只允许对同一个用户的密文进行同态变换，不能适用于多个接收者的情形。下面分别针对每种情况给出研究的技术路线：

4.1　单源单宿和多源单宿

对付这两种情况，直接用HE即可，源端对数据包均用接收端的公钥加密；中间网络节点利用同态属性对密文直接做编码混合；接收端对混合后的密文用自己的密钥解密获得混合后的明文，进而根据相应网络编码算法所规定的解码过程恢复出原来的数据包。

4.2　单源多宿

理论上，对付这种情形最直接的方案是大家熟知的广播加密(Broadcast Encryption，BE)。然而，为了允许中间编码节点对密文进行混合，还必须支持同态属性。根据我们所知，目前还没有同时支持广播和同态属性的加密方案。但是，我们可以利用具有密文同态属性的代理重加密(PRE)的思想提出一种变通的解决方案。代理重加密(PRE)允许中间代理将针对一个用户的密文转变为针对另一个人的密文，而且执行转换的中间代理并无法看到相应的明文信息。方案框架简单描述如图2所示：

图2　单源多宿加密及同态编码混合示意图

假设：系统参数大素数p=2kp′+1，p′也是素数，k根据消息空间来决定，越大加密越慢，但加密的消息越长。g是模p的原根(即p-1阶生成元)，g0=gp′mod p(则g0为2k阶生成元)。

每个用户选择自己的私钥x，要求x与p-1互素，公钥设置为y=gxmod p。

(1)源节点A先用自己的公钥对自己欲发出的数据包P进行加密得EA(P)，并计算针对所有它想发给的接收节点{ Bj}的代理重加密密钥{rkA→Bj}然后将(EA(P)，rkA→Bj)发送给下游节点。

(2)对数据包P加密：

假设Pi<2k选择随机数r，计算：

c1=grg0pimod p

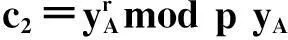
令EA(Pi)=(c1，c2)

(3)将(EA(Pi)，{rkA→Bj})发送给下游节点。编码节点C在收到单源节点A的多个不同的数据包后，对所有的EA(P)域对应的多个密文利用同态属性进行编码混合得到新的密文EA(Q)，然后将(EA(Q)，{rkA→Bj})作为编码后的数据包发送给下游节点后进行编码混合：

逐分量相乘：(a，b)△(a′，b′)=(a·a′mod p，b·b′mod p)

混合后：EA(Q)=EA(P1)△EA(P2)…△EA(Pm)=(A，B)

(EA(Q)，{rkA→Bj})作为编码后的数据包发送给下游节点。

(4)接收节点Bj在收到(EA(Q)，{rkA→Bj})后，先从{rkA→Bj}表中找到对应于自己的rkA→Bj，再利用rkA→Bj对密文EA(Q)进行转换，就得到了相当于用自己的公钥加密的数据包EBj(Q)，进而用它自己的私钥解密得到编码后的明文Q；最后，根据相应的网络编码算法规定的解码过程，从Q中解码得到对应的P。数据包P被源节点用自己的公钥加密，编码后的密文数据包EBj(Q)被接收节点用自己的私有解密。任何攻击者包括中间执行编码混合的中间节点都无法看到明文消息，即使知道了所有的重加密密钥也没有用处，因为重加密之后仍然是密文，没有对应的私钥，仍然是解不了密的。

重加密：A′=A，B′=BrkA→Bjmod p即EBj(Q)=(A′，B′)

解密：

算法JL描述如下：

1.Q=0，B=1；

2.For i=1 to k do

a)z=LS(Q’，p，2^i)，t=LS(g0，p，2^i)

b)if t<>z then Q=Q+B；

c)B=2B

3.Return Q

其中LS(a，p，d)=a^{(p-1)/d} mod p

4.3　多源多宿

这种情形目前理论上还未见有人研究。但是，借助于王绪安最近提出的新型的对偶重加密方案(Dual Proxy Re-Encryption，DPRE)，我们可以给出一种解决思路。DPRE跟传统PRE的最大区别在于：传统PRE中，重加密密钥是由原始解密人授权生成的；而DPRE中，重加密密钥可以由加密者生成。下面给出方案的简要描述如图3所示：

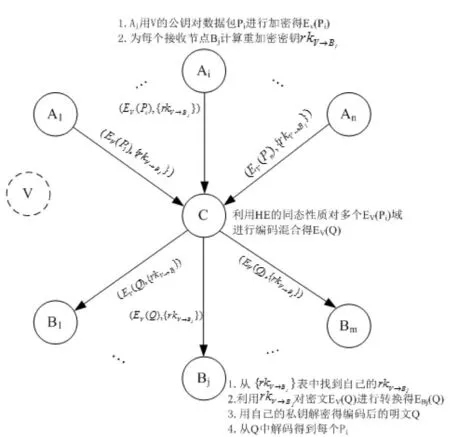
图3　多源多宿加密及同态编码混合示意图

(1)全系统共享一个虚拟节点V，V的私钥在其公钥生成之后立刻销毁——系统中任何人任何节点都不能也无需知道V的私钥。

(2)每个源节点Ai对自己欲发送的数据包Pi利用V的公钥进行加密得密文EV(Pi)，并为每个接收节点Bj生成代理重加密密钥rkV→Bj，最后将数据包(EV(Pi)，{rkV→Bj})发送给下游节点。

(3)编码节点C在收到多个(EV(Pi)，{rkV→Bj})之后，利用HE的同态性质对多个EV(Pi)进行编码混合得到新的数据包EV(Q)，并发送至下游节点。

(4)接收节点的操作跟单源多宿的情况相同。

5总结

上述安全网络编码算法轻量级实现的技术路线。在国际密码研究领域，轻量级密码技术近年来一直是个热点领域，而且也已经取得了不少成绩。这些技术均为本项目提供了很好的借鉴和启发：

(1)采纳Vilela等人最近在“Light weight Security for Network Coding”一文中的思想：加密操作实施在编码向量上足以保证安全性，而无需对大量的原始数据包进行加密。这样做，加密工作量和中间节点编码混合的工作量都明显减少。(当然，源端首先需要在对随机选取的编码向量加密，然后用编码向量明文对原始数据进行一次编码混合以防止第一站传递过程中别窃听。目的端只有解密出正确的编码向量明文，才可能实现正确的解码。)

(2)系统分析现有的轻量级密码实践技术。特别是轻量级公钥密码技术。目前被认可的“轻量级”公钥密码技术主要有两类：一是椭圆曲线密码ECC体制；二是NTRU格密码体制。因此，需要分析ECC和NTRU在实现轻量化方面的核心技术，进而对已有的一些重量级的PRE、PRS、HE、HS密码体制进行轻量化改造。在此基础上给出上述安全网络编码算法的“轻量化”设计。

参考文献：

[1]R Ahlswede，N Cai，S R Li，et al. Network information flow[J]. IEEE Transactions on Information Theory，2000，46(4)：1204-1216.

[2]Feldman J，Malkin T，Stein C，et al. On the capacity of secure network coding[C]. Proc 42nd Annual Allerton Conference on Communication，Control，and Computing，2004.

[3]Wu Y，Chou P A，Jain K. A comparison of network coding and tree packing[C]. ISIT 2004 Proceedings，International Symposium on Information Theory，2004：143.

[4]Jaggi S，Sanders P，Chou P A，et al. Polynomial time algorithms for multicast network code construction[J]. IEEE Transactions on Information Theory，2005，51(6)：1973-1982.

[5]Tan J，Médard M. Secure network coding with a cost criterion[C]. Modeling and Optimization in Mobile，Ad Hoc and Wireless Networks，2006 4th International Symposium on IEEE，2006：1-6.

[6]Silva D，Kschischang F R，Koetter R. A rank-metric approach to error control in random network coding[J]. IEEE Transactions on Information Theory，2008，54(9)：3951-3967.

[7]Silva D，Kschischang F R. Security for wiretap networks via rank-metric codes[C]. ISIT 2008，IEEE International Symposium on Information Theory. 2008：176-180.

[8]El Rouayheb S Y，Chaudhry M A R，Sprintson A. On the minimum number of transmissions in single-hop wireless coding networks[C]. Information Theory Workshop，IEEE，2007：120-125.

[9]El Rouayheb S Y，Soljanin E. On wiretap networks II[C]. ISIT 2007，IEEE International Symposium on Information Theory，2007：551-555.

[10]Bhattad K，Narayanan K R. Weakly secure network coding[J]. NetCod，Apr，2005，104.

[11]Silva D，Kschischang F R. Universal weakly secure network coding[C]. Networking and Information Theory，ITW 2009，IEEE Information Theory Workshop on，2009：281-285.

[12]Cai N，Yeung R W. A security condition for multi-source linear network coding[C]. ISIT 2007，IEEE International Symposium on Information Theory，2007：561-565.

[13]Chan T，Grant A. Capacity bounds for secure network coding[C]. Communications Theory Workshop，AusCTW 2008，Australian，IEEE，2008：95-100.

[14]Blaze M，Bleumer G，Strauss M. Divertible protocols and atomic proxy cryptography[M]. Springer Berlin Heidelberg：Advances in Cryptology—Eurocrypt 98，1998：127-144.

[15]Libert B，Vergnaud D. Unidirectional chosen-ciphertext secure proxy re-encryption[M]. Springer Berlin Heidelberg：Public Key Cryptography-PKC 2008，2008：360-379.

(责任编辑：王谦)