弯曲丝带有关物理现象的解析

弯曲丝带有关物理现象的解析

邱为钢*

(湖州师范学院理学院浙江 湖州313000)

*国家自然科学基金,项目编号：11475062，11275067；湖州师范学院中青年教师卓越教学能力培养计划专题项目，项目编号：2014ZYJH017作者简介：邱为钢(1975-), 男, 博士，副教授，主要从事大学物理的教学和研究.

摘 要：假设弹性势能正比于曲率平方，由变分原理，得到了重力场中旋转丝带的形状方程，并画出了图形.给出了向上竖直放置丝带开始弯曲时的临界长度精确值，以及向下竖直放置丝带开始弯曲时的临界转速与长度关系图.

关键词：弹性势能丝带临界值

收稿日期：(2014-09-30)

先从一个常见的生活现象开始，在宴会上水果拼盘处，常会看到一根细长的木杆，其底部绑着很多细细的丝带.当木杆处于不同状态时，其上的丝带对应呈现不同的分布状态:竖起来正放，丝带散开；旋转起来，丝带倾向于水平展开.倒放，丝带几乎成一直线；旋转，丝带也散开，如图1所示.

图1　实际生活中弯曲的丝带

(1)

其中s是弧长坐标，θ是曲线上一点切线与纵轴的夹角，ρ是质量密度，ω是转速，l是丝带的长度.物理量可以相加，其量纲必定相等.定义一个长度单位l0和频率单位ω0，式(1)中的前3项量纲相等，得到

于是得到长度单位

频率单位

(2)

(3)

由解析几何知识可知

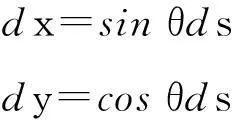
(4)

以及

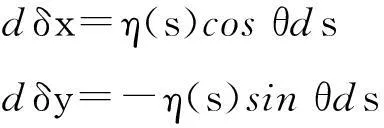
(5)

设

dG(s)=dsdH(s)=λxds

(6)

分部积分，并利用式(5)和式(6)，将式(3)中的积分项化为

(7)

式(3)中的边界项包含G(s1),H(s1),θ′(s1)等项.对于任意的η(s)，式(7)为零，于是得到弯曲丝带的形状方程

(8)

及边界条件

θ′(s1)=0H(s1)=0G(s1)=0

(9)

式(8)与文献[1]中利用弹性理论得到的方程一致.数值计算中，丝带下端固定为原点，起始条件是

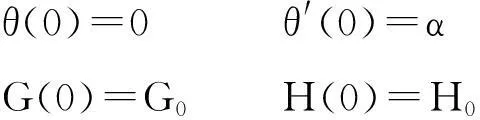
(10)

数值求解式(4)和式(8)，由边界条件式(10)反过来确定式(9)中的参数α,G0,H0，就能确定丝带的形状.

考虑第一个问题，当弹性系数k固定时，丝带竖直正放，长度至少达到多长(临界长度lc)，丝带才开始弯曲.先定性分析，长度大，不弯曲，重力势能大,弹性势能为零；长度大而弯下来，重力势能减小，但弹性势能增大；所以丝带有一个临界长度，超过这个临界长度，丝带开始弯曲.文献[2]以圆木为例，半定量分析得到

其中Yr2相当于本文中的弹性系数k，但没有给出比例系数.利用本文给出的方程式(4)和式(8)，数值计算发现，临界长度的定量结果是lc=1.994 4l0.

图2　竖直正放丝带临界转速与长度的理论关系图

由图2可以看出，竖直正放的丝带，长度越大，使丝带开始弯曲的转速越小，当长度趋向于临界长度lc时，转速趋向于零.当丝带长度为l=1.5l0，转速比例系数分别为λ=1.45，λ=1.5，λ=1.8，λ=2.2，λ=3.0，λ=4.0时，丝带形状如图3所示.

图3　竖直正放长度为l=1.5l 0的丝带在不同转速下的形状

由图3可以看出，转速越大，丝带越往外伸展.当丝带长度为l=2.5l0，转速比例系数分别为λ=0.0，λ=0.5，λ=1.0，λ=2.0，λ=3.0，λ=4.5时，丝带形状如图4所示.

图4　竖直正放长度为l=2.5l 0的丝带在不同转速下的形状

由图4可以看出，转速越大，丝带越向外伸展.

第三个问题是，当丝带竖直倒放时，转速至少达到多大(临界转速ωc)时，丝带才开始弯曲.这个临界值依赖于丝带的长度.数值计算得到的临界转速ωc与丝带长度l的关系如图5所示.

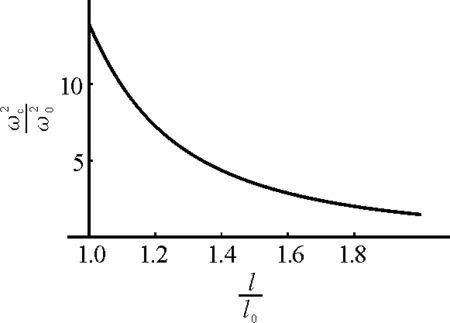
图5　竖直倒放丝带临界转速与长度的理论关系图

图6　竖直倒放长度为l=1.5l 0的丝带在不同转速下的形状

由图5看出，丝带长度越大，临界转速越小，当丝带长度趋向无穷大时，临界转速趋向于零.当丝带长度为l=1.5l0，转速比例系数分别为λ=2.5，λ=3.5，λ=3.8，λ=4.0，λ=4.3，λ=4.6，λ=5.0，λ=5.5时,丝带形状如图6所示.

当丝带长度为l=2.5l0，转速比例系数分别为λ=1.1，λ=1.2，λ=1.4，λ=1.6，λ=1.8，λ=2.0，λ=2.2，λ=2.5时,丝带形状如图7所示.

图7　竖直倒放长度为l=2.5l 0的丝带在不同转速下的形状

由图6和图7可以看出，丝带越长，转动的弯曲效应越明显.

转动丝带模型中有3个因素对形状施加影响，重力倾向于拉低，离心力倾向于离开转轴，弹性势能倾向于不弯曲，三者共同作用，使得丝带呈现多种形状.在这个模型中，重力加速度、弹性系数不能改变，是固定的，但是长度和转速是可以调控的，这就给实验设计提供了方便，有兴趣的读者不妨试试，测量转动丝带的各种物理量和几何量，对本文的理论预言进行验证.

参 考 文 献

1朗道，粟弗席兹.弹性理论(第5版).北京：高等教育出版社，2011.80～82

2赵凯华.定性与半定量物理学(第2版).北京：高等教育出版社，2008.85～86

ExplanationonthePhysicalPhenomenon

RelatingtotheBentRibbon

QiuWeigang

(SchoolofScience,HuzhouTeachersCollege,Huzhou,Zhejiang, 313000)

Abstract:The shape equation of bending ribbon is derived from variation principle with the assumption that the elastic potential is proportional to the square of curvature. The theoretical shape is drawn from numerical results. The exact critical length of up-ribbon is given and theoretical curve of critical speed of revolution via length of down-ribbon are also drawn.

Keywords:elasticpotential;ribbon;criticalvalue