降雨作用下高路堑边坡渗透稳定性分析

秦　龙　廖　俊

(贵州省交通规划勘察设计研究院股份有限公司　贵阳　550081)

降雨作用下高路堑边坡渗透稳定性分析

秦龙廖俊

(贵州省交通规划勘察设计研究院股份有限公司贵阳550081)

摘要为了探讨边坡在强降雨作用下的渗流情况和稳定性，采用Geostudio中的SEEP/W模块对边坡在降雨作用下渗流情况进行数值计算分析，再与SEEP/W模块进行耦合分析，采用Morgenstern-Price法计算边坡在强降雨作用下的安全系数，并分析其稳定性。

关键词渗流计算耦合分析安全系数稳定性分析

1降雨入渗SEEP/W理论

1.1达西定律

SEEP/W模块渗流是以饱和和非饱和的达西定律为主的，达西定律的表达式为

q=ki

(1)

式中：q为流速，m/s；k为渗透系数，其值等于水力梯度为1时水的渗透速度，m/s；i为水力梯度。

1.2渗流基本方程

渗流计算的一般微分方程为

(2)

式中：H为总水头，m；kx为x方向渗透系数，m/s；ky为y方向渗透系数，m/s；Q为边界流量，m3/s；θ为单位体积含水率； t为时间，s。

在稳定流条件下，任何时刻单元水流入和流出的体积是相等的，则方程右边为0，有

(3)

土体体积含水率与土的性质和应力状态有关[1]。饱和-非饱和情况下的应力状态可以用状态变量为σ-ua和ua-uw来表示。式中：σ为总应力；ua为空隙内气体压力，uw为孔隙水压力。

SEEP/W在计算过程中的总应力是不变的，即土体没有发生加载或者卸荷[2]。SEEP/W还假定对于非稳定流问题，空隙中的气体压力为一常量[3]，意味着σ-ua也是一常量。因此，单位体积含水率的变化仅与孔隙水压力的变化有关，并可用下式来表达：

(4)

式中：mw为土-水关系函数的斜率。

总水头H定义为

(5)

式中：uw为孔隙水压力；可改写为uw=H-y；γw为水的容重；y为相对高程。

空隙水压力uw可改写为uw=h-y，将式(5)代入式(4)有

(6)

把式(6)代入式(2)得

(7)

由于高程是个常量，y对时间的导数为0，最终SEEP/W中的控制方程为

(8)

2降雨作用下边坡渗流数值计算分析

2.1工程概况

本文研究边坡高68m，形成7级台阶。根据工程地质钻探资料，出露地层从上至下为第四系残积层粘土，下伏基岩为前震旦系板溪群清水江组薄层状板岩，分强、中风化2层，产状30°∠25°，其材料物理力学参数见表1。

表1　材料物理力学参数表

2.2计算模型建立

对边坡在降雨作用下的边坡渗流数值计算分析，本文选取典型横断面作为渗流数值计算分析模型建立的基础，然后在SEEP/W模块中建立有限元渗流计算分析模型，见图1。

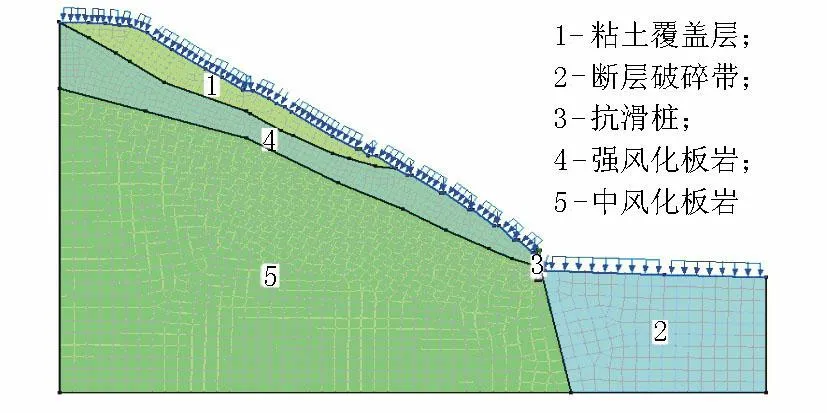
图1　渗流计算模型

2.3边界条件

根据该地区的气象资料，1d内的单位降雨量为1.52×10-6m/s。边坡开挖后对坡面采取相应的防护措施，在降雨过程中大部分雨水沿着坡面流动，只有少部分渗入到坡体内部，本文经过多次验算，最终选取单位降雨量的1/10 000m/s作为本次渗流计算的边界条件，即渗流边界条件为1.52×10-10m/s。

2.4计算结果及分析

为了分析该边坡在强降雨作用下边坡体内的渗流情况，本人计算了不同降雨时间下边坡体内渗流等势线变化情况，其结果见图2。

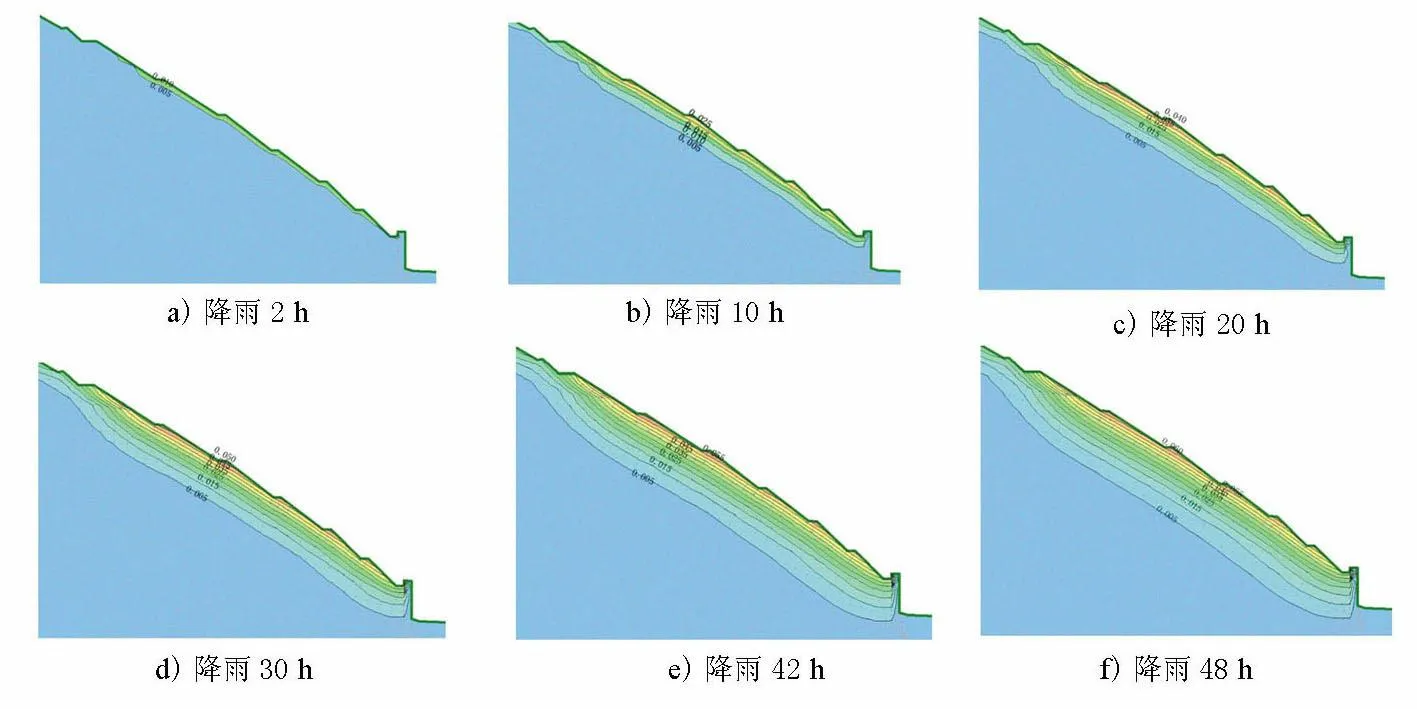
图2　不同降雨时间下边坡体内渗流变化图(单位：m)

根据以上计算得出不同时刻边坡体内最大降雨渗透水头，整理出边坡体内最大渗透空隙水水头随时间的变化曲线，见图3。

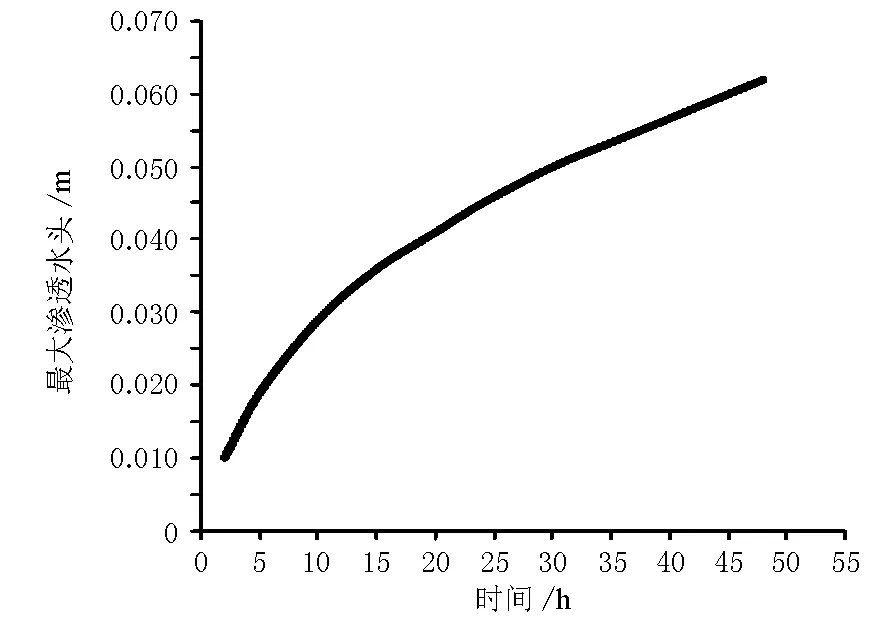
图3　边坡体内最大渗透空隙水水头随时间变化曲线

从以上不同降雨时间下边坡体内渗流变化情况图和图3可以看出，随着降雨时间增加，边坡体内雨水渗透范围逐渐扩大，边坡体内的最大渗透空隙水水头也不断增大。

3边坡稳定性计算分析

对边坡稳定性分析，本文将Geostudio中的SLOPE/W模块和SLOPE/W模块进行结合，采用Morgenstern-Price法进行该边坡的稳定性计算分析。前面计算分析了不同降雨时间下边坡体内渗透变化情况，然后根据不同的降雨时间下边坡体内雨水渗透的范围确定不同降雨时间下边坡体内潜在滑动面的范围，以此作为边坡稳定性计算分析的基础。

在计算边坡稳定性时，潜在滑动面的位置是根据雨水渗透范围大小确定的，计算得到不同降雨时间下对应边坡安全系数变化情况见图4。

收稿日期：2014-09-30

DOI10.3963/j.issn.1671-7570.2015.01.028