基于双强度折减法对边坡稳定性的分析

邹济韬　王　磊

(贵州交通规划勘察设计研究院股份有限公司　贵阳　550081)

基于双强度折减法对边坡稳定性的分析

邹济韬王磊

(贵州交通规划勘察设计研究院股份有限公司贵阳550081)

摘要均质边坡的二维稳定性分析常使用强度折减法，方法中2个强度指标c，φ采用同一个折减系数，但是c，φ各自的安全储备不同，单一的折减系数不能反映它们的衰减特性。文中针对工程实例中的某一均质边坡先后采用折减c，φ的方法定量分析其稳定性，旨在得到更加符合实际的折减系数和更能准确地反映c，φ各自的安全储备。

关键词均质边坡稳定性双强度折减法

1双强度折减法的原理

边坡发生滑动时，其滑面的c与φ衰减特性是不同的，主要是表现在[1-3]：土体的粘聚力c，可以理解为滑体内部连接键断裂时所需要的能量；土体的内摩擦角φ，可以理解为滑体的土颗粒间在剪切移动时相互的摩擦作用。当c所提供的粘聚力抵抗不了下滑力时，滑面与滑床之间内部连接键发生断裂以致滑体发生剪切破坏，φ所提供的摩阻力这时就开始发挥作用。也就是说滑面的c与φ衰减特性不同，发挥作用的先后顺序和程度也不同。所以，在运用强度折减法分析边坡稳定性时，应采用不同的折减系数，即双折减系数[4-6]。双强度折减法是在将岩土体强度参数c，φ逐渐降低直到其达到破坏状态为止，即将c，φ值同时除以折减系数Fc和Fφ,得到一组新的强度指标c′，φ′[7-8]。

(1)

(2)

本文将双强度折减法应用于大型有限元分析设计软件Ansys中，已达到充分发挥双强度折减法在分析岩土介质破裂过程方面的优势，求出相应稳定性安全系数的目的。

2数值分析实例

2.1工程概况、参数选取，以及建模相关假设

该边坡位于贵州省某高速公路之间，地势较高，以高山为主，岩性主要由均质碳酸盐岩构成。边坡坡脚α约为60°左右，坡高H为16.6m，根据工程地质勘察资料，岸坡岩体基本质量级别为III级(按照《工程岩体分级标准》(GB50218))。根据相关的实验测试，以及《工程岩体分级标准》(GB50218)，φ为50°～39°，c为1.5～0.7MPa。综合考虑上述各因素再结合工程实例类比，该边坡岩体物理力学参数为重度γ=26.5kN/m3，弹性模量E=30GPa，泊松比μ=0.25，见表1。

表1　岩土体物理力学参数

为消除边界影响, 模拟范围向坡脚和坡后适当延伸, 坡脚向外延伸0.5倍坡高, 坡后延伸1.5～2.0倍坡高，计算模型见图1。

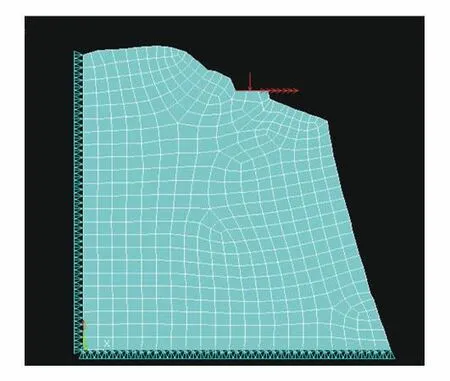
图1　计算模型

2.2计算与分析

本例中以塑性区是否连通作为边坡破坏的判定依据，以X方向的位移作为边坡滑动程度的说明。通过分析4种有限元数值模拟结果，来研究c，φ在边坡滑动时各自的发挥程度与发挥的秩序，以及衰减速度与程度。

2.2.1传统的单一强度折减

折减系数从1.10起开始计算，当发现塑性应变云图中变形区有连通趋势时进行折减系数加密(每次只增加0.02)。计算结果见表2，达到极限状态时的结果见图2。

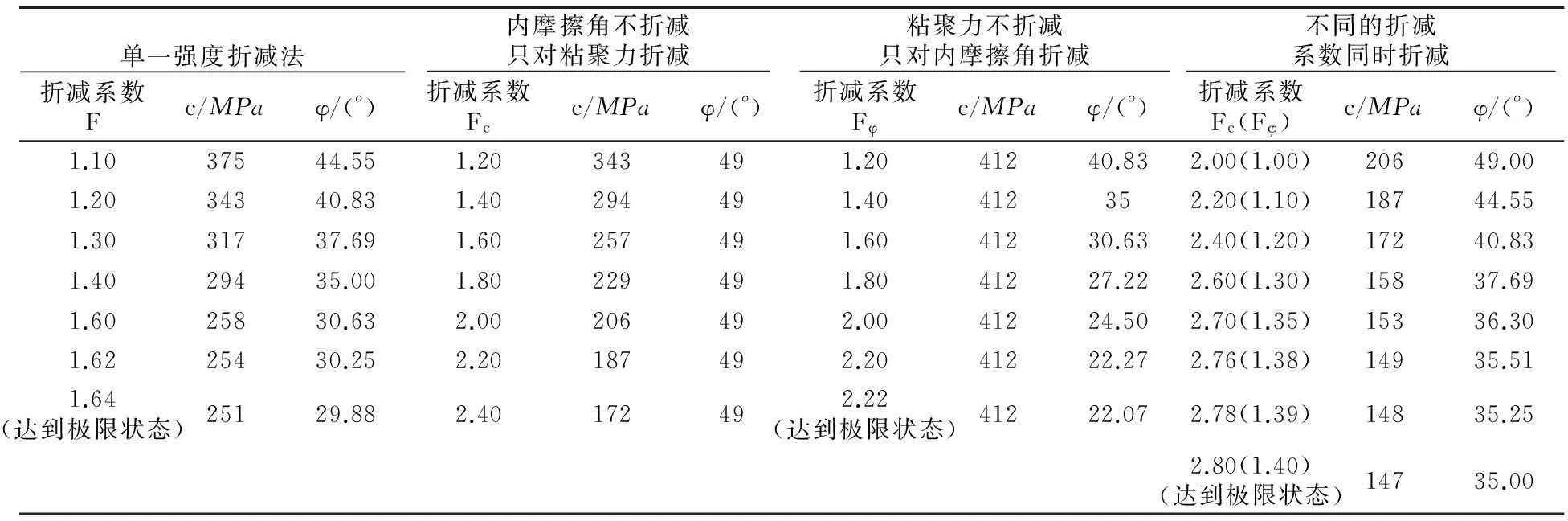
表2　计算结果数据表

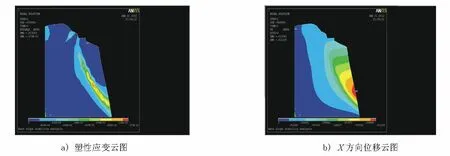
图2　F=1.64时的塑性应变X方向位移云图

2.2.2φ不折减只对c折减

φ的强度折减系数Fφ保持1不变，c的折减系数Fc从1.20(每次以0.2增加)开始计算,计算结果见表2。由表2可见φ对该边坡稳定性做出了较大贡献，φ不减小，c快速衰减边坡也能保持稳定。即可以得出结论：均质岩坡发生滑动破坏时φ充分发挥作用，然后才由c作补充以便发挥最大的抗滑力。

2.2.3c不折减只对φ折减

本例为另一种极端的情况，c的强度折减系数Fc取为1，φ折减系数Fφ从1.20(每次以0.2增加)起开始计算，当发现塑性应变云图中变形区有连通趋势时进行折减系数加密(每次只增加0.02)。折减系数见表2,达到极限状态时的结果见图3。

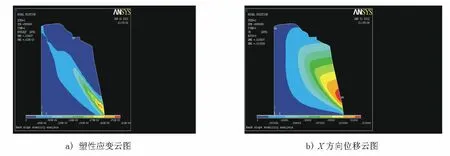
图3　c不折减只对Fφ折减(Fφ=2.22时)

从表2中的结果再一次说明了上述的推断。φ对本例中边坡的稳定有较大贡献，即c保持不变，但只要φ减小，边坡仍然有破坏的可能性。不过，从图3看到塑性应变云图的变形区已经连通到边坡的后缘，这和利用单一折减系数时的结果不符，造成的原因可能是假定的极端状态，所以下面对c，φ以不同的折减系数同时折减。

2.2.4c，φ以不同的折减系数同时折减

在实际的边坡发生滑动时，c，φ同时发挥作用。假定2个折减系数成一定比例进行配套折减[4-6]，配套折减以双折减系数比值(K=Fc/Fφ)来实现，其大小的依据主要是c，φ不同的衰减速度和衰减程度。

通过对上面的2种极端情况的讨论可见，Fφ

图4　Fc，Fφ同时折减(Fc=2.80，Fφ=1.40时)

从图2和图4对比中可以分析出，两者的塑性应变云图的变形区的形状比较相像，X方向位移最大值也基本相等。滑面土体φ在边坡的稳定性中起主要作用，边坡产生滑动时，只有φ值没有迅速破坏，岩体就能产生抵抗滑动的抗滑力。

3结论

(1) 比较传统折减法和双强度折减法2种情况时可以发现X方向位移和塑性变形基本相同，两者的数值见表3。由表3可见双强度折减法的X方向最大位移和最大塑性应变都要比传统的强度折减法的数据小，2种方法都能很好地反映岩土体稳定性分析中c，φ的强度储备，但后者更能表明c，φ各自对于边坡稳定做出的贡献。

表3　数据对比表

(2) 双强度折减是传统的强度折减法的扩展，所以分析结果与传统的方法大致相同，但考虑到2个强度指标以不同速率折减，其结果就可以更能准确地反映c,φ各自安全储备。通过Ansys程序可自动求得塑性区连通面，能够跟踪边坡滑动破坏面起裂、发展和滑动面的形成过程。

参考文献

[1]ZIENKIEWICZOC,HUMPHESONC,LEWISRW.Associatedandnon-associatedviscoplasticityandplasiticityinsoilmechanics[J].Geotechnique,1975,25(4):671-689.

[2]连镇营，韩国城，孔宪京.强度折减有限元法研究开挖边坡的稳定性[J].岩土工程学报，2001,23(4)：407-411.

[3]钟才根，张斌.采用不同Drucker-Prager屈服准则得到的边坡安全系数的转换[J].岩土力学，2011，32(12)：3751-3755.

[4]郑颖人，赵尚毅，李安洪，等.有限元极限分析法及其在边坡中的应用[M].北京: 人民交通出版社,2011.

[5]唐芬，郑颖人.边坡稳定安全储备的双折减系数推导[J].重庆交通大学学报：自然科学版，2007(4):95-100.

[6]唐芬,郑颖人,赵尚毅.土坡渐进破坏的双安全系数讨论[J].岩石力学与工程学报,2007,26(7):1402-1407.

[7]赵尚毅, 郑颖人,刘明维,等.基于Drucker-Prager准则的边坡安全系数定义及其转换[J].岩石力学与工程学报,2006, 25(S1):2730-2734.

[8]唐春安，李连崇，李常文，等.岩土工程稳定性分析RFPA强度折减法[J].岩石力学与工程学报,2006,25(8):1522-1530.

收稿日期：2014-09-30

DOI10.3963/j.issn.1671-7570.2015.01.019