两种地图点群综合算法的比较

李　赟,闫浩文,刘正军

(1.兰州交通大学测绘与地理信息学院，甘肃兰州730070；2 中国测绘科学研究院，北京100830)



两种地图点群综合算法的比较

李赟1,2,闫浩文1,刘正军2

(1.兰州交通大学测绘与地理信息学院，甘肃兰州730070；2 中国测绘科学研究院，北京100830)

摘要：通过搭建实验程序，分别对基于非加权Voronoi图和加权Voronoi图的点群自动综合算法进行验证，详细对比和分析两种算法计算结果对点群的统计信息、拓扑信息、度量信息和专题信息的传递情况，计算部分结果的相似度，从而得出加权Voronoi图点群综合算法更优的结论。

关键词：传统Voronoi图；加权Voronoi图；点群综合；算法；相似度

数字地图在比例尺变化的过程中产生地图符号拥挤、堆叠和冲突等问题。要使得地图清晰可读，在地图比例尺改变的过程中必须采取一些必要的操作(如：选择、简化、聚合等)来化简地图要素，这个过程称之为地图综合[1]。

点群是地图上常见的要素，如在中小比例尺地图中的城市、岛屿群等，分析单个目标点信息没有意义，值得关心的是群体分布所隐含的空间结构化信息[2]。综合结果的质量评估是基于点群空间分布结构化信息的，主要是通过建立指标，对点群综合前后空间分布结构化信息的对比[3]。点群目标典型的结构化特点有分布范围轮廓形状、密度、纹理结构特征等[4]，综合前后的结果应该在分布模式、分布范围、相对密度等方面保持相似关系。因此，量化计算综合前后点群的相似度是算法评估的常用方法[5-6]。点群综合过程中涉及的主要操作是选择保留点，即通过“选取”算子实现点群自动综合，选取的标准应符合地图综合过程中尽可能传递重要信息的原则。对现有的算法进行归纳，需要传递的信息有4类：统计信息、专题信息、度量信息和拓扑信息[1,7-9]。点群的统计信息是点数；专题信息是点的权值，通过对考察问题量化得到；度量信息包括点的局部密度、相对密度、点群分布范围(分布多边形)；拓扑信息为点的Voronoi邻居[1,7-9]。

目前已有的点群综合算法有居民地空间比率算法、分布系数算法、重力模型算法、圆增长算法、基于四叉树的算法、点地图化简算法、顾及空间特征的算法、Kohonen网络算法、基于Voronoi图的算法和基于加权Voronoi图的算法[6]。其中前6种算法只部分顾及了4类信息，第7、8种算法未能给出综合结果对信息传输的量化评价。后2种算法顾及4类信息，算法9使用Ordinary Voronoi Diagram (简称OVD)为工具来表达点的影响范围，算法10在算法9的基础上使用改进的Multiplicatively Weighted Voronoi Diagram (简称MWVD)来替代OVD。由于后2种算法对信息传递考虑比较全面，且具有相关性，故本文通过实验对后2种算法进行对比和分析。

1OVD和MWVD算法

1.1　基本概念

1)选取法则：确定地图上的点数，可采用：

其中，Nf为被选取的点数，N0为综合前的点数，S0为综合前地图比例尺分母，Sf为综合后地图比例尺分母。

2)虚拟边界点：为了消除边界点和内点差异化的处理方法，并且更符合真实边界带状分布的特征，人为定义一组边界点。原始点群全部位于虚拟边界的内部。

3)Voronoi图可以很好的表达地物要素的影响区域，算法中使用Voronoi图来处理几何度量信息和拓扑信息。

4)点的重要性程度值：重要性程度值属于专题信息，反映不同点的重要性程度。

5)点的选取概率：表示某一点在下一轮删除中被保留的概率，该值在算法中作为点是否被保留的参考，由点的重要性程度值和点的Voronoi图面积共同确定。

1.2　OVD算法

OVD算法有以下3个步骤：

1)构造新点集：先构造原始点群的Delaunay三角网，由此搜索一条包含所有初始点的多边形，该多边形的顶点就是边界点。然后构造一条新的边界多边形，使得该多边形的每一条边和初始点的边界多边形对应且平行，新多边形称为虚拟边界，虚拟边界的顶点为虚拟边界点。虚拟边界点和初始边界点的距离等于初始边界上边长的平均值。虚拟边界点和初始点共同构成了新点集。

2)基于Voronoi图的点群反复综合：构造新点集的Voronoi图，根据

3)确定最后保留在结果地图上的点数：设最后一轮删除地图上保留点数为n1，倒数第二轮删除地图上保留点数为n2，若|Nf-n1|<|Nf-n2|，则综合结果保留点数为n1，反之为n2。

1.3　MWVD算法

MWVD算法基本步骤和OVD算法相似，也具有3个步骤[10-14]：

1)构造新点集：同OVD算法，找到初始点的边界多边形。连接初始点边界多边形质心和边界点，并向外延伸得到虚拟边界顶点，延伸长度与该射线通过的初始边界点相关联的三角形边长的平均值。顺次连接各延长线顶点就得到了虚拟边界多边形。

2)基于MWVD的点群反复综合：①构造包含虚拟点在内的新点群的MWVD；②利用

计算每个点的选取概率Pi，Ai是第i点的Voronoi多边形面积；③点群初始点都赋以“自由”的状态，综合过程中还会产生“固定”和“被删”的状态；④把“自由”点按选取概率的升序排列；⑤找出“自由”点中选取概率最小的一个，若该点所有邻居点都是自由的，则标记该点为“被删”，并固定其所有邻居点，返回④；否则把“固定”点改为“自由”点，结束本轮删除。

3)确定最后保留在结果地图上的点数：方法同OVD算法。

1.4　两种算法比较

本文从以下方面对两种算法进行对比:

1)统计信息。即点数，用最终结果保留的点数和用基本选取法则计算的理论值做对比。

2)专题信息。分别计算综合前后点群重要性程度值，对比两种算法在综合过程中对专题信息的传递效果。

3)度量信息。计算综合前后点群的分布多边形，从多边形相似性来判定综合结果对点群分布范围的传递情况。

2实验研究

程序采用C#语言编写，设计自定义文件格式，支持文件读写，鼠标绘制点群，计算Delaunay三角网、加权和非加权Voronoi图、边界多边形等，并对OVD和MWVD点群综合算法均进行了实现，还支持单步查看每一轮删除结果的功能。此外，程序实现统计综合前后点群专题信息(重要性程度值)、相对局部密度和分布边界等信息的功能。

2.1　实验1

选取四川省1~3级城市的点群数据，共156个点。城市点群综合是常见的点群综合性问题，在综合过程中，等级高的城市应尽可能被保留，且要顾及点群分布密度。原数据见图1。

图1　四川省156个城市点群数据(1级126个，2级29个，3级1个)

实验中设定原始地图比例尺分母为S0=10 000,目标地图比例尺分母为Sf=50 000,MWVD算法和OVD算法的综合结果见图2。

图2　四川省城市点群数据综合结果

1)根据选取的基本法则计算得到的目标地图点数为69。MWVD算法综合后点数为59，OVD算法结果为66。可以看出OVD算法的综合结果保留点数更接近按基本选取法则计算的结果，OVD算法总共进行了4轮删除，每一轮删除的点数分别为29、24、21、16；WMVD算法进行了3轮删除，每一轮删除的点数为44、30、23。结论：MWVD算法每一轮删除点的“幅度”比OVD算法大，效率更高。

2)综合前点的重要性程度平均值为1.198 718，综合后MWVD算法结果为1.423 729，OVD算法为1.287 879。可见在综合过程中，MWVD算法更好的保留了重要性程度大的点。

3)MWVD算法和OVD算法综合前后的点群分布范围见图3。图中实线为原始点群分布范围，虚线为综合后点群的分布范围。原始点群分布多边形面积为92 492 610.86，MWVD与OVD算法计算结果点群的分布多边形面积分别为101 269 409.51、105 851 225.30，相对面积分别为1.095、1.144。由此可知，MWVD算法计算结果的分布多边形与原始点群分布多边形面积相似比更大。从形态上观察，MWVD算法计算结果的分布多边形也与原始点群分布多边形重合度更大。

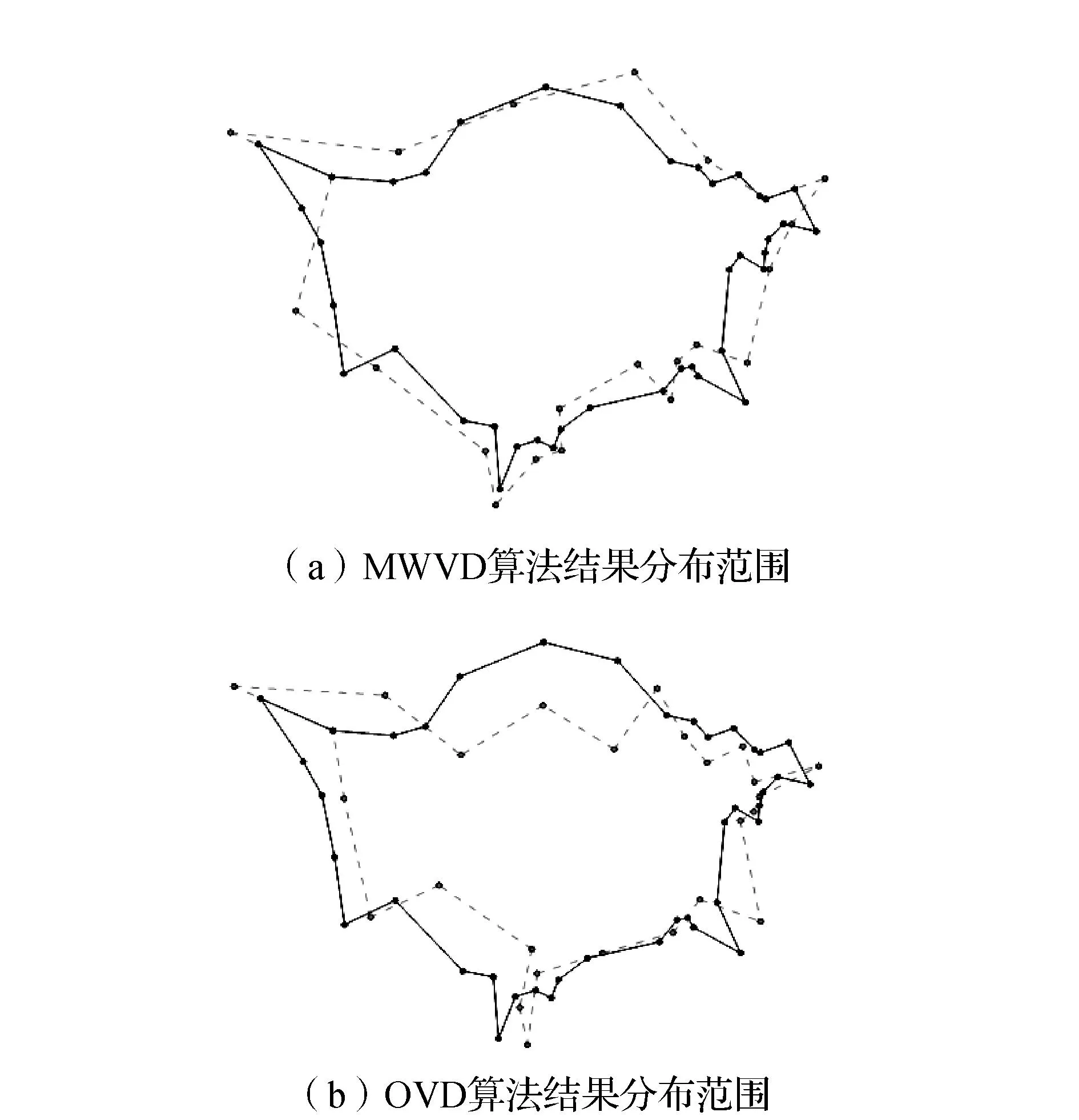
图3　四川省城市点群数据分布范围(虚线为综合后数据分布范围)

2.2　实验2

模拟了两组数据，具有两种不同等级的点(1和2)见图4。数据1点分布均匀的特点，电线杆塔的分布，包含51个点；数据2分布狭长，呈带状分布，包含40个点。实验参数同实验1。

1)数据1原始数据包含51个点，基本选取法则计算结果为22个点，经过MWVD算法综合后剩余18个点(经3轮删除)，经过OVD算法综合后剩余21个点(经5轮删除)；数据2原始数据包含40个点，基本选取法则计算结果为17个点，经过MWVD算法综合后剩余20个点(经3轮删除，取第2轮删除的结果)，经过OVD算法综合后剩余18个点(经5轮删除，去第4轮删除的结果)。再次验证了MWVD算法效率高的结论。

2)数据1综合前重要性程度值的平均值为1.215 686，经MWVD算法综合后为1.5，经OVD算法综合后为1.476 19；数据2综合前重要性程度值的平均值为1.2，经MWVD算法综合后为1.4，经OVD算法综合后为1.388 889。两组数据的实验中，MWVD算法对重要性程值得传播率略高于OVD算法。此外，点群中重要性程度值高的点数越少，MWVD算法和OVD算法综合后点群的重要性程度值的平均值越接近。

3)两组数据经两种算法综合后的分布多边形见图5。

从表1中可以看出，MWVD算法的计算结果分布多边形面积相似比结果更优。

图4　两组模拟数据

图5　两组数据综合前后分布范围(虚线为综合后)

原始点群分布多边形面积MWVD计算结果分布多边形面积OVD计算结果分布多边形面积MWVD计算结果面积相似比OVD计算结果面积相似比数据185959768.2390410791.7827342477.691.050.32数据2152688127.55151357841.8176259107.250.990.50

3结束语

本文对OVD和MWVD点群综合算法的实验结果进行对比分析，验证两种算法的可行性。通过对比，基于MWVD点群综合算法在效率、综合结果的各项信息的传递中效果更优。本文讨论的两种算法属于图的点群综合算法，具有很高的时间复杂度，如何有效地提高效率有待进一步研究。另外，点群自动综合算法结果需在分布模式、分布范围、相对密度等方面保持相似关系，因此相似度计算的研究将应该作为地图综合算法的必要补充。

参考文献：

[1]YAN H W,WEIBEL R.An algorithm for point cluster generalization based on the Voronoi diagram [J].Computers and GeoSciences,2008,34(8):939-954.

[2]艾廷华，刘耀林.保持空间分布特征的群点化简方法[J].测绘学报，2002，31(2)：175-181.

[3]牛继强，徐丰，姚高伟.点群多尺度表达不确定性评估方法研究[J].测绘科学，2011，36(4)：75-77.

[4]郭庆胜.点状要素群的结构化及其在综合中的应用[J].测绘学院学报，1999，16(3)，210-213.

[5]梅耀元，闫浩文，李强.多尺度地理空间点状要素相思关系研究[J].测绘与空间地理信息，2010，33(2)：18-20.

[6]刘涛，杜清运，闫浩文.空间点群目标相似度计算[J].武汉大学学报(信息科学版)，2011，36(10)：1149-1153.

[7]闫浩文，王家耀.基于Voronoi图的点群目标普适综合算法[J].中国图象图形学报，2005，10(5)：633-636.

[8]闫浩文，王邦松.地图点群综合的加权Voronoi算法[J].武汉大学学报(信息科学版)，2013，38(9)：1088-1091.

[9]陈静静，闫浩文.应用一级邻近点生成加权Voronoi图的思想[J].重庆工学院学报(自然科学版)，2008，22(1)：85-88.

[10]蒙印，艾廷华，杨井源.1∶250 000水系要素综合缩编技术方法[J].测绘与空间地理信息，2014，37(3):201-203.

[11]夏永亮.基于复杂网络理论的城市道路网络自动综合方法[J].测绘与空间地理信息，2014，37(8):155-156.

[12]于艳平，沈婕，尚在颖.点群选取与化简算法时间复杂度研究[J].南京师大学报(自然科学版)，2012，35(1)：111-116.

[13]武芳，王家耀.地图自动综合概念框架分析与研究[J].测绘工程，2002，11(2)：18-20，48.

[14]王辉连，武芳，王宝山，等.用于数字地图自动综合的多边形合并算法[J].测绘工程，2005，14(3)：15-18.

[责任编辑：李铭娜]

Comparison of two point cluster generalization algorithms

LI Yun1，2,YAN Hao-wen1,LIU Zheng-jun2

(1.School of Geomatics,Lanzhou Jiaotong University,Lanzhou 730070,China；2.Chinese Academy of Surveying & Mapping,Beijing 100830,China)

Abstract：A test program is build up, in which the OVD-based and MWVD-based algorithms for point cluster generalization are verified.The statistical,topological,metric and thematic information transmissions during the process of generalization are analyzed in details. The similarities of some of the results are also calculated,thus the MWVD-based algorithm is proved to be better.

Key words：ordinary Voronoi diagrams；multiplicative weighted Voronoi diagrams；point cluster generalization；algorithms；similarity

作者简介：李赟(1986-),男，硕士研究生.

基金项目：国家自然科学基金资助项目(40871208)

收稿日期：2014-09-20

中图分类号：P283.1

文献标识码：A

文章编号：1006-7949(2015)12-0043-05