坐标转换Partial-EIV总体最小二乘方法
王乐洋,郑玄威,申兴林,许光煜,于冬冬
(1.东华理工大学测绘工程学院,江西南昌330013;2.流域生态与地理环境监测国家测绘地理信息局重点实验室,江西南昌330013;3.江西省数字国土重点实验室,江西南昌330013)
坐标转换Partial-EIV总体最小二乘方法
王乐洋1,2,3,郑玄威1,申兴林1,许光煜1,于冬冬1
(1.东华理工大学测绘工程学院,江西南昌330013;2.流域生态与地理环境监测国家测绘地理信息局重点实验室,江西南昌330013;3.江西省数字国土重点实验室,江西南昌330013)
摘要:在测量数据处理过程中,针对系数矩阵中同时存在随机元素和固定元素的情况,Xu等通过将随机元素分离使EIV模型推广到Partial-EIV模型,并给出基于Partial-EIV模型的总体最小二乘(TLS)算法。文中介绍该算法,并将其应用在平面及空间的坐标转换中,通过与最小二乘(LS)、总体最小二乘(TLS)及加权总体最小二乘(WTLS)方法的比较和分析,验证该算法有效性。
关键词:总体最小二乘;Partial-EIV模型;函数模型;系数矩阵;坐标转换

在大地测量数据处理中,经典最小二乘方法用的最为普遍。该方法仅考虑了观测向量的噪声,而认为观测方程的系数矩阵中元素为非随机量,然而系数矩阵含有随机误差的情况在测量数据处理实践中是存在的。在某些测量数据的处理中,系数矩阵中元素并不总是由固定元素组成,往往包含一些观测量。如大地测量反演[1,2]、坐标转换[3]等数学模型中,观测向量和系数矩阵均由观测数据组成,两者都包含随机误差,这类平差模型被称之为EIV模型。此时,利用经典最小二乘对其进行处理显然不恰当。针对此类模型的求解,Adcock于1877年首次提出了所有观测数据的残差的平方和最小化的总体最小二乘平差准则[4]。1980年Golub和Van Loan针对EIV模型提出了SVD(singular value decomposition)算法,即奇异值分解算法,并首次采用Total Least Squares(TLS)命名总体最小二乘[5]。针对系数矩阵中元素的多样性,专家学者纷纷提出各种对应的解决方案,如针对EIV模型中系数矩阵含有特殊结构的混合总体最小二乘法(LS-TLS)[6,7];系数矩阵出现重复元素的多元整体最小二乘法[8];采用特定的定权方法固定不需要修正的常数元素的加权整体最小二乘法[9]。对于系数矩阵中随机和固定元素同时存在的一般情况,Xu等通过将系数矩阵中的随机元素与常数元素相分离的方法,将EIV模型扩展为更为一般的表现形式的Partial-EIV模型,并推导基于Partial-EIV模型的总体最小二乘解,且给出在有限样本下的总体最小二乘解的精度评定计算式[10]。基于Partial-EIV模型的总体最小二乘算法,并将其应用在坐标转换中,通过平面坐标和空间坐标转换两个算例,证明该算法在坐标转换中的适用性和有效性。
1总体最小二乘法
总体最小二乘方法相比于传统最小二乘方法不仅考虑观测向量中的误差,也考虑系数矩阵中存在的误差,其函数模型为[11-13]
(1)
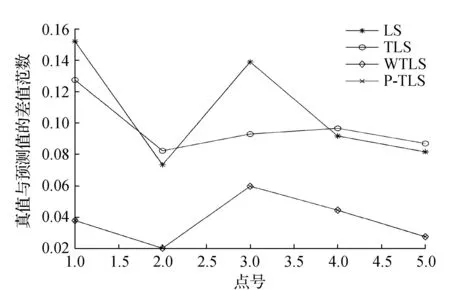
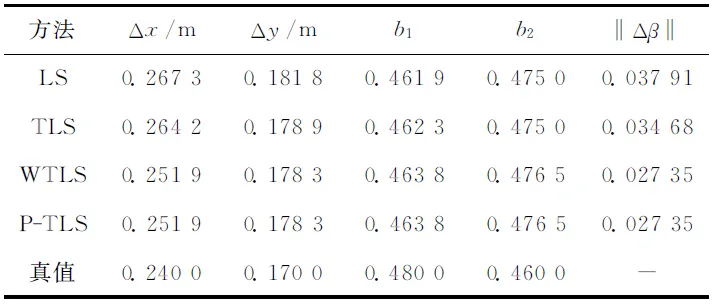
式中:A是n×m的系数矩阵且Rank(A)=m 假设系数矩阵及观测向量之间相互独立且为不等精度观测,则其随机模型为 (2) 2基于Partial-EIV模型的总体最小二乘算法 当系数矩阵A中出现非随机性的固定元素,将导致其协因数阵奇异,因此必须对其进行特殊的处理才能得到唯一的加权TLS解。而针对这种情况,Xu等将EIV模型改写并称之为Partial-EIV模型[10] (3) (4) (5) (6) (7) (8) 式(8)中 (9) 式(6)可写成 (10) 于是由式(10)可得[10] (11) 3算例及分析 平面坐标转换的四参数模型为[14] 当控制点个数为i(i≥2)时,四参数转换模型为 分别用最小二乘(LS)、总体最小二乘(TLS)、加权总体最小二乘(WTLS)和基于Partial-EIV模型的TLS方法(以下简述为P-TLS)求取坐标转换参数β的估值及参数估值与真值差值的二范数‖Δβ‖,其结果如表2所示。 表1 模拟数据及相应权值 表2 不同方法结果列表 通过表2结果看出,P-TLS方法和WTLS方法得到结果一致且最好,离真值最为接近;LS方法得到的结果最差;TLS方法得到的结果要稍好于LS方法而差于其他两种方法。上述结果从以下几个方面解释:①LS法只考虑了观测向量的误差,而忽略系数矩阵中存在的误差,得到的结果与参数真值偏差较大;②TLS法考虑观测向量和系数矩阵中的误差,结果优于LS法,但与参数真值相比,偏差还是较大;③在P-TLS和WTLS方法中,着重考虑了观测向量和系数矩阵中元素不等精度的情况,所以结果优于TLS法,得到更加接近真值的结果。 在空间三维坐标转换中,当旋转角是小角度或初始已知,且控制点数不小于3个时,布尔沙转换模型可写成: 利用算例1中4种方法分别求解参数的估值,得到的结果如表4所示。 表3 模拟数据及相应权值 表4 不同方法求解结果 详细介绍几种方法之间的差异,在表3中随机选取5个点,将其坐标设为起始坐标,分别利用表4中4种方法求解得到的7个参数值求得这5个点的目标坐标的估值。每种方法得到的5个点坐标的估值与真值的差值范数图如图1所示。 图1 预测点坐标真值与估值的差值范数 从表4中结果可以得出,基于Partial-EIV模型的TLS法所求参数结果和加权总体最小二乘(WTLS)方法得到的结果一致,且优于其他两种方法,得到的参数估值与真值的差值范数最小,这与算例1中得到的结论相一致。从图1也可以看出,在4种方法当中,利用P-TLS和WTLS方法得到的转换参数求得的5个点的估值相比TLS和LS方法要更为接近真值。综合算例1和算例2的结果可以得出,在系数矩阵和观测向量同时含有误差的情况下,基于Partial-EIV模型的总体最小二乘方法在解决坐标转换问题中能够得到更加理想的结果,验证了该方法在坐标转换问题中的适用性和有效性。 4结束语 本文详细地介绍当观测方程的系数矩阵和观测向量同时存在误差时基于Partial-EIV模型下的总体最小二乘算法,通过平面坐标转换和空间坐标转换两个算例,表明该算法在解决坐标转换问题中的可靠性和有效性。对于该算法在其他方面的适用性和有效性还需进一步研究。 参考文献: [1]鲍建宽,李永利,李秀海.大地坐标转换模型及其应用[J].测绘工程,2013,22(3):56-60. [2]杨娟,陶叶青.稳健估计下的坐标系统转换总体最小二乘算法[J].测绘科学,2015,40(4):15-18. [3]杨强,党亚民,章传银,等.地壳运动动力响应模型构建研究[J].测绘工程,2014,23(4):6-9. [4]ADCOCK R J.Note on the Method of Least Squares[J].The Analyst,1877,4(6):183-184. [5]GOLUB G H,VAN LOAN C F.An Analysis of the Total Least Squares Problem[J].SIAM Journal on Numerical Analysis,1980,17 (6):883-893. [6]陆珏,陈义,郑波.总体最小二乘方法在三维坐标转换中的应用[J].大地测量与地球动力学,2008,28(5):77-81. [7]冯剑桥,黄张裕,徐秀杰,等.总体最小二乘法在坐标转换中的应用[J].测绘与空间地理信息,2014,37(7):205-206. [8]SCHAFFRIN B,FELUS Y A.On The Multivariate Total Least-squares Approach to Empirical Coordinate Transformations.Three Algorithms[J].Journal of Geodesy,2008,82(6):373-383. [9]SCHAFFRIN B,WIESER A.On Weighted Total Least-squares Adjustment for Linear Regression[J].Journal of Geodesy,2008,82(7):415-421. [10]XU P L,LIU J N,SHI C.Total Least Squares Adjustment in Partial Errors-in-variables Models:Algorithm and Statistical Analysis[J].Journal of Geodesy,2012,86(8):661-675. [11]王乐洋.基于总体最小二乘的大地测量反演理论及应用研究[D].武汉:武汉大学,2011. [12]王乐洋,许才军,温扬茂.利用STLN和InSAR数据反演2008年青海大柴旦Mw6.3级地震断层参数[J].测绘学报,2013,42(2):168-176. [13]王乐洋.测边网坐标的总体最小二乘平差方法[J].大地测量与地球动力学,2012,32(6):81-85. [14]JAZAERI S,AMIRI-SIMKOOEI A R,SHARIFI M A.Iterative algorithm for weighted total least squares adjustment.Survey Review,2014,46(334):19-27. [责任编辑:李铭娜] Partial-EIV total least squares method for coordinate transformation WANG Le-yang1,2,3,ZHENG Xuan-wei1,SHEN Xing-lin1,XU Guang-yu1,YU Dong-dong1 (1.School of Geomatics,East China Institute of Technology,Nanchang 330013,China;2.Key Laboratory of Watershed Ecology and Geographical Environment Monitoring,NASG,Nanchang 330013,China;3.Jiangxi Key Lab for Digital Land,Nanchang 330013,China) Abstract:In geodetic data processing,the situation that the random and fixed elements exist simultaneously in coefficient matrix will be common.To solve this problem,Xu (Xu et al,2012) expands the EIV model to Partial-EIV model and proposes a total least squares method to the new adjustment model.In this paper,the algorithm proposed by Xu is introduced and applied to the plane and space coordinate transformation.The examples compare four methods (LS,TLS,WTLS and the introduced algorithm) and the effectiveness is tested through the result. Key words:total least squares;Partial-EIV model;function model;coefficient matrix;coordinate transformation 作者简介:王乐洋(1983-),男,副教授,博士,硕士生导师. 基金项目:国家自然科学基金资助项目(41204003,41161069,41304020);测绘地理信息公益性行业科研专项项目(201512026);江西省自然科学基金资助项目(20132BAB216004);江西省教育厅科技项目(GJJ13456,KJLD12077,KJLD14049);地理空间信息工程国家测绘地理信息局重点实验室项目(201308);东华理工大学博士科研启动金(DHBK201113) 收稿日期:2014-12-08;修回日期:2015-05-08 中图分类号:P207 文献标识码:A 文章编号:1006-7949(2015)12-0012-05
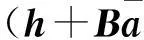






3.1 平面坐标转换



3.2 空间三维坐标转换