微型控制器领域的数理逻辑基础的推理

微型控制器领域的数理逻辑基础的推理

刘妍

(烟台职业学院，山东 烟台 264670)

摘要：微型控制器已经应用到我们的生活的各个领域，例如飞机上各种仪表的控制、计算机的网络通讯与数据传输、工业自动化过程的实时控制和数据处理、家用电器、医疗设备等等。微型控制器的功能越来越强大，离不开位于中央处理单元CPU中算术逻辑运算单元ALU的加法器的支持。本文论述了微型控制器的运算处理的数理逻辑的推理。

关键词：微型控制器；加法器；数制；补码

收稿日期：2015-03-16

作者简介：刘妍(1978-)，女，山东莱阳人，烟台职业学院教师.

中图分类号：TN4文献标识码：A

1问题的引出

在我们生活中的各个领域，处处可见微型控制器忙碌的身影，它将采集到的的信号进行智能化、微型化、数字化的处理，并将这些操作交给由复杂指令系统构成的程序来实现特定的功能，如电梯智能化管理，压力、温度、湿度的测量等等。

微型控制器采用大规模集成电路作为逻辑元件， 将各种复杂的操作交由运算器(ALU)处理，而ALU的核心处理单元为加法器，操作数以补码形式进行运算。

本文论证了以补码形式参与运算的数理逻辑的推理。

2二进制

电脑诞生的时候是用二极管做的,二极管作为计算的最小单位部件，需要电力来驱动,电流只存在2种状况，通和不通,于是产生了二进制。二进制数也可以用十六进制数、十进制数等形式表示。

以8位处理器的MCS-51系列单片机为例，该系列单片机采用正逻辑，电路的高电平和低电平对应二进制数1、0，计算的工作原理基于“布尔代数”[1]，进行逻辑运算，单片机电路虽然复杂，但基本单元却很简单，由与门、或门、非门等组成。

逻辑运算又称布尔运算，布尔用数学方法研究逻辑问题，成功地建立了逻辑演算。他用等式表示判断，把推理看作等逻辑运算式的变换。这种变换的有效性不依赖人们对符号的解释，只依赖于符号的组合规律。这一逻辑理论人们常称它为布尔代数。20世纪30年代，逻辑代数在电路系统上获得应用，随后，由于电子技术与计算机的发展，出现各种复杂的大系统，它们的变换规律也遵守布尔所揭示的规律。

由布尔运算可知，逻辑运算与算术运算都可以以代数演算的形式运算，在数学运算方法方面是统一的，基本运算方法是四则运算。

3码制

微型控制器CPU的核心处理单元ALU的核心单元加法器，是怎样实现四则运算的呢？

四则运算为加法运算、减法运算、乘法运算、除法运算。乘法运算可以由数的移位相加运算实现，除法可以由数的移位相减实现；这样四则运算可以归结为加法运算和减法运算。

为了将减法运算由加法运算实现，微型控制器中引入了负数的概念。8位机中约定，最高位D7表示符号，其他7位表示数值，D7=1表示负数，D7=0表示正数。

例1：4=0000 0100B，[+4]原=0000 0100B，[+4]反=0000 0100B，[+4]补=0000 0100B；

在例1的二进制数中，加黑色标注的最高位为符号位，黑色标注的低7位为数值位。

3.1 无符号数

由于加法运算中1+1=10，1111 1111B+1=10000 0000B，而MCS-51系列单片机的存储器的位数是8位的，能够存储的是8位二进制数，进行加法运算时由于存储器位数的限制，使得8位无符号二进制最大数1111 1111B加1在存储器中存储的结果变为最小数0000 0000B。8位无符号数的范围为FFH-00H。我们以循环的形式将8位无符号数进行排列：

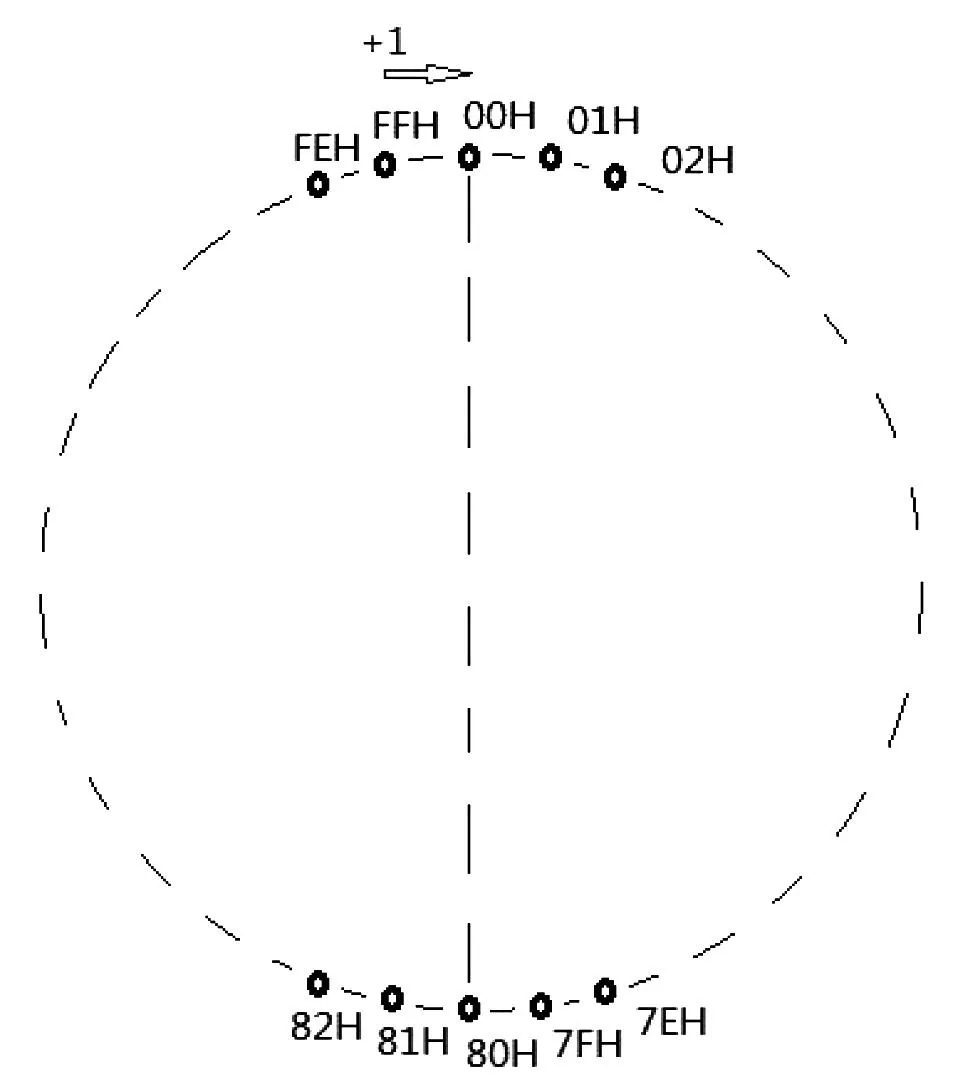
图1　8位无符号数的循环排列

从图1中可以看出，将数据从00H-FFH顺时针圆形循环排列，规则为加1；FFH加1后得到00H。

3.2 8位有符号数

一个有符号数用原码、反码、补码三种方式表示[2]。

①8位有符号数原码

原码：正数的原码与原来的数相同；负数的原码符号位要置1，数值位保持不变。

例2：1=0000 0001B，[+1]原=0000 0001B=01H，

[-1]原=1000 0001B=81H；

例3：2=0000 0010B，[+2]原=0000 0010B=02H，

[-2]原=1000 0010B=82H；

例4:126=0111 1110B，[+126]原=0111 1110B=7EH，

[-126]原=1111 1110B=FEH；

例5：127=0111 1111B，[+127]原=0111 1111B=7FH，

[-127]原=1111 1111B=FFH；

8位有符号数原码表示的范围为-127-+127，因为：

[+0]原=0000 0000B=00H，[-0]原=10000000B=80H；

我们以循环的形式将8位有符号数原码进行排列：

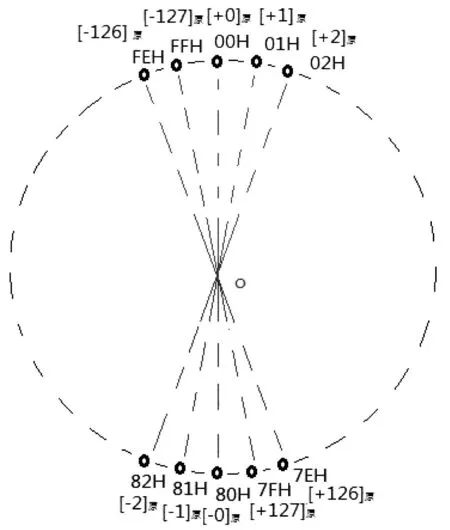
图2　8位有符号数原码循环排列

由图2中可以观察到正数原码和负数原码围绕圆心O对称排列，由于[+0]原和[-0]原不相等，所以原码不能直接参与到运算中。

②8位有符号数反码

反码：正数的反码表示与正数的原码相同；负数的反码符号位为1，数值位由其绝对值按位取反得到。

例6：1=0000 0001B，[+1]反=0000 0001B=01H，

[-1]反=1111 1110B=FEH；

例7：2=0000 0010B，[+2]反=0000 0010B=02H，

[-2]反=1111 1101B=FDH；

例8:126=0111 1110B，[+126]反=0111 1110B=7EH，

[-126]反=1000 0001B=81H；

例9:127=0111 1111B，[+127]反=0111 1111B=7FH；

[-127]反=1000 0000B=80H；

8位有符号数反码表示的范围为-127-+127，因为：

[+0]反=0000 0000B=00H，[-0]反=11111111B=FFH；

我们以循环的形式将8位有符号数反码进行排列：

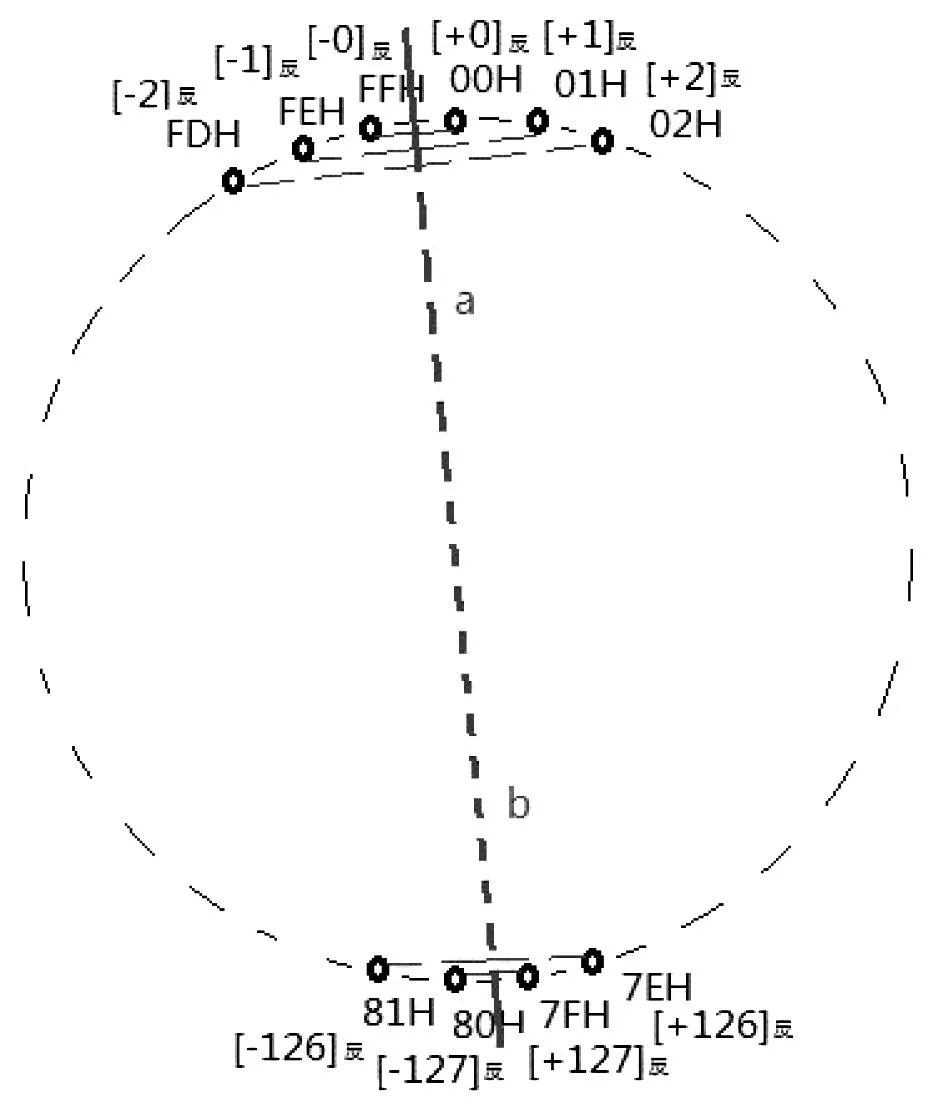
图3　8位有符号数反码循环排列

由图3中可以观察到，正数反码和负数反码围绕轴ab平行对称排列，由于[+0]反和[-0]反不相等，所以反码不能直接参与到运算中。

③8位有符号数补码

补码：正数的补码与正数的原码相同；负数的补码为其反码加1得到。

例10：1=0000 0001B，[+1]补=0000 0001B=01H，

[-1]补=1111 1111B=FFH；

例11：2=0000 0010B，[+2]补=0000 0010B=02H，

[-2]补=1111 1110B=FEH；

例12:126=0111 1110B，[+126]补=0111 1110B=7EH，

[-126]补=1000 0010B=82H；

例9:127=0111 1111B，[+127]补=0111 1111B=7FH；

[-127]补=1000 0001B=81H；

8位有符号数补码表示的范围为-128-+127，因为：

[+0]补=0000 0000B=00H，

[-0]补=[-0]反+1=1111 1111B+1=0000 0000B=00H；

规定，[-128]补=80H，-128没有对应的原码和反码。

我们以循环的形式将8位有符号数补码进行排列：

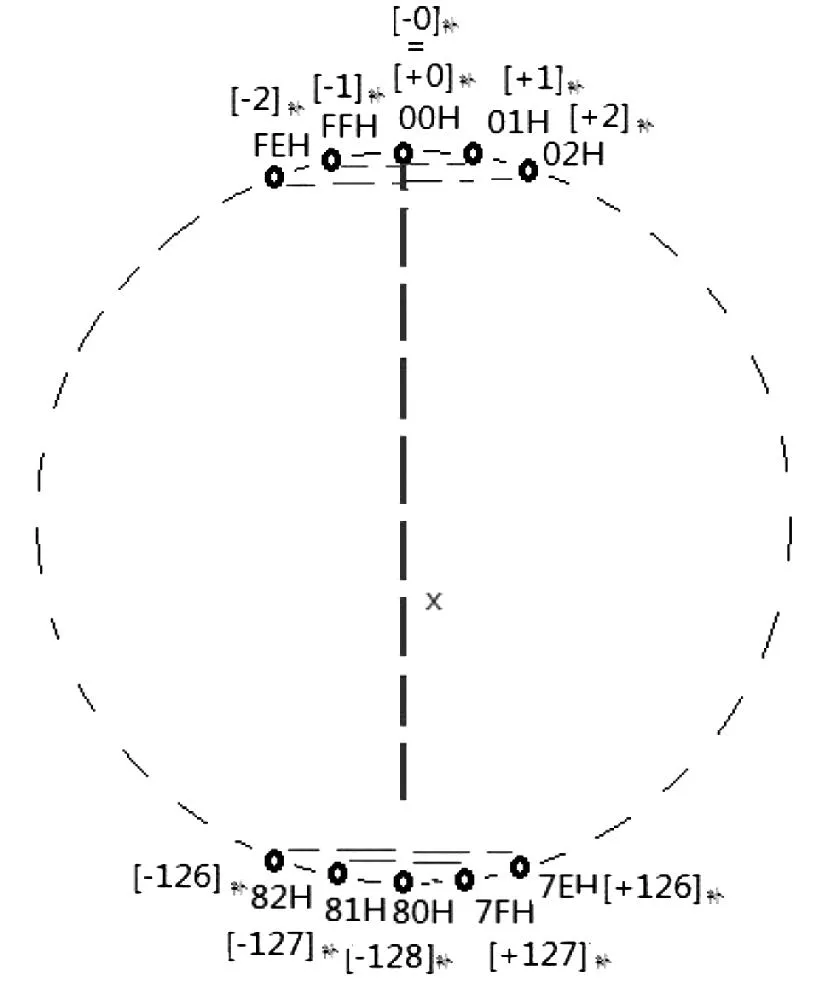
图4　8位有符号数补码循环排列

由图4中可以观察到，正数补码和负数补码围绕轴0x平行对称排列，[+0]补和[-0]补相等。

将图4按照我们所熟悉的数轴形式展开，如图5：

(a)区间在-128~+127的补码标注形式数轴

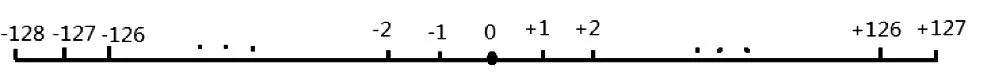
图5(b)区间在-128~+127的传统十进制数标注形式数轴

观察图5(a)与图5(b)，可以看出，二者表达的数理关系是一致的，所以我们能够使用补码形式参与运算。

4微型控制器算术逻辑运算单元

以MCS-51系列单片机为例，内部有一个8位的CPU，由核心处理单元ALU实现算术逻辑运算，如图6。

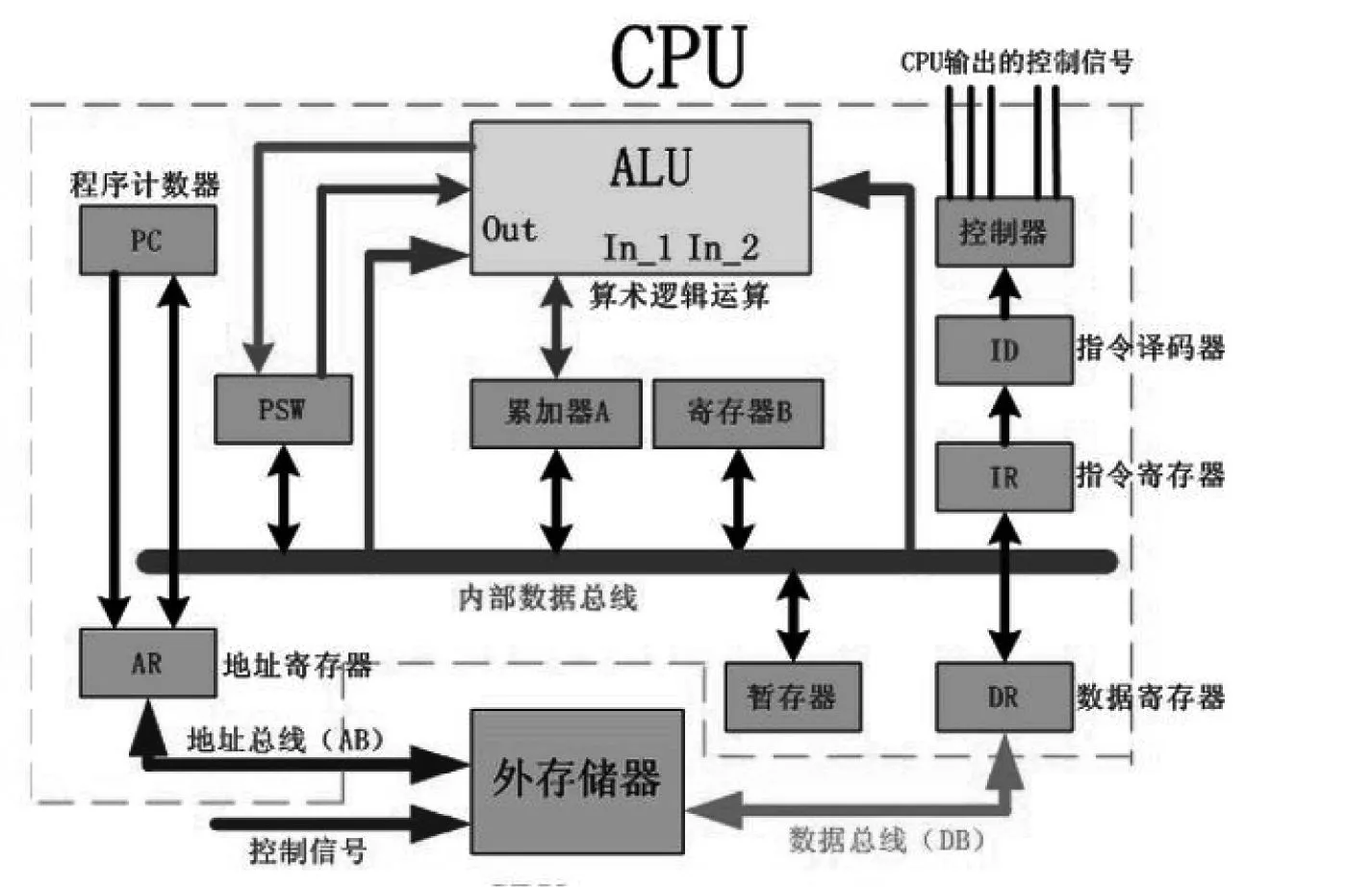
图6　CPU内部结构框图

运算器(ALU)的主要功能[3]

A)算术和逻辑运算，可对半字节(一个字节是8位，半个字节就是4位)和单字节数据进行操作。

B)加、减、乘、除、加1、减1、比较等算术运算。

C)与、或、异或、求补、循环等逻辑运算。

D)位处理功能(即布尔处理器)。

5结论

使用补码参与运算可以将减法运算转变成为有符号数的加法运算，这样四则运算可以由加法器完成，通过布尔代数的原则，中央处理器CPU可以实现算术与逻辑运算，完成对微型控制器各种数据的处理。

参考文献：

[1]杨炳儒.布尔代数及其泛化结构[M].北京：科学出版社，2008.

[2]张志良.单片机原理与控制技术[M].北京：机械工业出版社，2005.

[3]丁元杰.单片微机原理及应用[M].北京：机械工业出版社，1999.

(责任编辑侯中岩)