多相机数码影像光束法解算及精度分析

多相机数码影像光束法解算及精度分析

赵海强，李浩，钱海明，仝红菊

(河海大学地球科学与工程学院，江苏南京210098)

摘要：光束法算法通常用于解决同一相机影像的平差解算问题，文中探讨多相机数码影像的光束法解算方法，理论研究与实验分析相结合，研究建立多相机影像光束法的平差模型，并在相同条件下与单相机光束法解算结果相比较。结果表明，多相机数码影像光束法严密平差可解，且分别在不同的控制条件下与单相机光束法解算精度相当。

关键词：多相机；光束法；数码影像；精度；畸变参数

中图分类号：P23文献标志码：A

收稿日期：2014-02-17

基金项目：国家自然科学基金资助项目(51079053)；江苏省自然科学基金资助项目(SBK201221489)

作者简介：赵海强(1988-)，男，硕士研究生.

Calculationandprecisionanalysisofbundleadjustmentofmulti-cameradigitalimages

ZHAOHai-qiang，LIHao，QIANHai-ming，TONGHong-ju

(SchoolofEarthSciencesandEngineering，HohaiUniversity，Nanjing210098，China)

Abstract：Bundle adjustment algorithm is commonly used to solve the problem of the same camera images. This paper will explore the bundle adjustment of multi-camera digital images for the first time，by combining theoretical research and experimental analysis to establish the bundle adjustment model of multi-camera，and to compare the results with a single camera under the same conditions. The results show that the bundle adjustment of multi-camera digital images can be solved，and get similar accuracy with a single camera under the control of different conditions.

Keywords：multi-camera;bundleadjustment;digitalimages;accuracy;distortionparameters

近景摄影测量因其快捷和非接触测量方式[1]广泛应用在工程、工业和建筑等各个领域[2]。而普通数码相机以其体积小、质量轻、方便使用、灵活性强等特点已广泛应用在近景摄影测量中[3]。目前，在大多数近景摄影测量工作中常使用同一数码相机获取原始影像数据，按传统光束法平差模型严密解算获取物方点点位坐标。然而，实际工程应用情况复杂多样，外业影像数据的采集并不总是采用同一台相机完成，一些项目将两台或者更多的相机搭载到同一个平台下获取设定重叠度的原始影像，或者直接采用不同的相机拍摄获取数码影像，同样得到立体模型，将一台相机的拍摄任务转换为两台或更多台相机完成，每台相机有其各自的相机内参数。正是这个原因，与单相机影像的数据处理不同，多相机影像内业数据处理的相机内参数部分将会被重新考虑，那么怎样构建相应的光束法平差模型就成为了空三加密的新问题。相机参数包含有内方位元素和相机的畸变参数。单相机光束法中这部分参数的平差模型矩阵块将在多相机光束法平差中重新配置，多套相机参数的光束法平差是一种新的解题思路。分析传统光束法解算模型，将相机参数的表达分解为不同的解算矩阵模块使得多相机的光束法解算成为可能。本文将以此为研究出发点，提出多相机数码影像的光束法解算，并结合试验数据，对解算成果进行分析。

1附加参数的多相机光束法平差模型

光束法区域网平差以共线条件方程为基础[4]，以每张像片所组成的一束光线作为平差计算的基本单元[5]，普通数码相机存在径向畸变差和切向畸变差两类系统误差，加入附加参数[6]补偿系统误差可提高平差解算精度[7]。

畸变差由如下多项式表达：

(1)

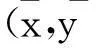
将以上畸变差改正多项式带入共线方程可得

(2)

根据以上共线方程式，像点坐标视作观测值，考虑相机的内方位元素、畸变系数以及各片外方位元素参数为未知数，其误差方程式可表示为

(3)

式中：ΔXS,ΔYS,ΔZS,Δφ,Δω,Δκ为像片外方位近似值改正数;Δx0,Δy0,Δf为内方位近似值改正数;Δk1,Δk2,Δp1,Δp2为畸变系数近似值改正数;ΔX,ΔY,ΔZ为物方坐标近似值改正数。

单相机光束法误差方程式的矩阵形式[8-9]为

V=AX+BZ+Ct-L.

(4)

式中：X表示像片外方位近似值改正数矩阵，Z表示内方位和畸变系数近似值改正数矩阵，C表示物方坐标近似值改正数矩阵。

将以上式子，按像点数，像片数展开得

(5)

按以上矩阵构建规律，可以推得多相机光束法误差方程式的矩阵结构为

(6)

为不破坏误差方程式的单一性和法方程式的带状结构，同时顾及到外业点已知坐标误差的影响,可把已知的外业坐标也按观测值加入坐标改正数。因此，控制点按检查点的误差方程式的形式列立附加误差方程式，即

(7)

式中：viX,viY,viZ为控制点坐标误差改正数，ΔXi,ΔYi,ΔZi为控制点坐标近似值改正数。

则带附加方程的多相机光束法平差误差方程式为

(8)

将外方位、内方位、畸变系数改正数用统一矩阵表示，可将法方程式整体概括为

(9)

式中：Δ1表示各像片相机参数改正数向量，包含X′，Z′向量。Δ2表示各点地面坐标的改正数向量，包含向量t′。

2实验与分析

本次试验的摄影目标为室内精密三维控制场，控制场分为3个层面，第1层在最前面，第2、3层依次向后。在控制场上共有47个点，可根据实验方案设计选择不同的控制条件和检查点，第1层点号：101～117，第2层点号：203～213，第3层点号：301～319，点位均匀分布。

实验分别采用Canon G5，Canon 5D和Canon G1X 3种不同型号的普通数码相机获取影像数据。拍摄焦距G5为7 mm，G1X为15 mm，5D为15 mm。拍摄为近距离拍摄，多相机摄影方式与普通单相机摄影测量拍摄方式一样，在获取下一张影像时换另一台相机即可。

实验1：

两不同相机与单相机实验对比，采用Canon G5(左片)和Canon G1X(右片)，单相机(左/右片)采用Canon G5。

以下两种方案拍摄环境、条件均一样，在不同的控制条件下进行。

方案1：当控制点较多，控制条件较好时，选择29个控制点，10个检查点，在3个控制层面上均匀选择点位。

方案2：控制点较少，控制条件一般，选择9个控制点，10个检查点，在3个控制层面上均匀选择点位。

实验计算结果如表1、表2所示。

表1　相机参数解算结果

表2　检查点坐标中误差 　mm

实验2：

采用3个不同相机获取的影像带入多相机光束法算法中计算，采用Canon G5(左片)、Canon 5D(中片)和Canon G1X(右片)，同样采用两种方案。

方案1：选择9个控制点，16个检查点，在3个控制层面上均匀选择点位。

方案2：选择28个控制点，16个检查点，在3个控制层面上均匀选择点位。

实验结果如表3、表4所示。

表3　相机参数解算结果

表4　检查点坐标中误差 　mm

以上两组实验已验证附加参数的多相机光束法可解算得到各相机的相机参数以及加密点坐标。从两种方案的检查点坐标中误差可以看出，在相同的条件下，多相机解算结果与单相机解算结果精度相当，单从多相机计算结果可知，不同条件下的两种方案，当控制点较少时，点位误差较大。

此两组实验已经证明多相机光束法解算是可行的，且能正确计算出物方点坐标，但能否很好地解算相机参数，需要进一步验证。

验证方案为：假设解算出来的相机参数(每个相机的3个内方位，4个畸变系数)为已知值应用，按照严密空间后方交会，解算出来各片外方位元素，再经过多片前方交会，直接解算出作为验证的控制点的解算坐标与实际坐标比较，即可分析相机参数的正确性。

按照验证方案的设计，对之前实验1的两种方案做进一步探讨，验证不同相机的内方位及畸变参数可以在多相机光束法中得到正确解算。验证共采用14个已知物方坐标的点作为验证点，两种方案验证结果如表5所示。

表5　验证点坐标中误差 　mm

经以上验证方案验证，两组实验方案解算得到的验证点点位中误差在交会方向Z向较大，在3 mm内。在控制条件一般时仍能在X,Y方向得到较精确的三维点位坐标数据，误差在1 mm以内。经验证多相机数码影像光束法整体平差解算得到的相机参数结果具有良好精度。

综合以上实验可以得到，多相机数码影像光束法需要考虑到各相机所对应的各自相机参数参与平差过程，光束法解算可得到各相机的相机参数及加密点点位坐标，检查点解算结果与同样条件下的单相机光束法结算结果精度相当，经进一步验证，多相机光束法解算的各相机参数结果精度良好。

3结束语

通过附加多套相机参数的光束法进行整体平差解算，可以得到各相机所对应的相机参数，同时解算出正确的加密点的物方坐标，并经进一步验证可以检验解算出的相机参数精度良好，多相机的光束法解算的可行性得到初步验证。本实验是对于两个不同相机的验证，对于影响精度的因素以及两个以上相机的光束法算法，以及解算速度和精度的提高方法可作为下一步的研究方向进行探讨。

参考文献：

[1]冯文灏.近景摄影测量[M].武汉：武汉大学出版社，2002.

[2]张曼祺，李浩，陈新玺.普通数码影像的光束法算法探讨[J].测绘通报，2006(6):10-12.

[3]陈建华，张雷，阮善发.非量测相机同步摄影控制器[J].南京工业大学学报:自然科学版,2003，25(5):92-94.

[4]邹瑜,雷蓉,纪松，等.地面几何标定的定向片自检校光束法区域网平差模型[J].测绘工程,2012,21(5)：8-12.

[5]何辉明，胡伍生，王克宇.摄影测量光束法加密精度的分析[J].测绘通报,2004(2):13-15.

[6]李德仁.自检校光束法区域网平差的相关分析和附加参数显著性检验[J].武汉大学学报：信息科学版，1981，6(2):46-64.

[7]TSAI V J.Automatic Photo Reordering in a Simultaneous Bundle Adjustment [J].PE&RS，1995，1(7)：899-908

[8]王建梅,朱紫阳.利用已有像控点的多期航空影像光束法区域网联合平差[J].测绘学报，2010,39(1)：22-27.

[9]袁修孝，季顺平，谢酬.基于已知定向参数影像的光束法区域网平差[J].武汉大学学报：信息科学版,2005,30(11):955-959.

[责任编辑：刘文霞]