基于灰色系统模型的 IGS 精密钟差预报
基于灰色系统模型的IGS精密钟差预报
潘绍林,张显云,杜宁,范旭亮,张俊
(贵州大学矿业学院,贵州贵阳550025)
摘要:钟差是精密单点定位中的重要误差源,IGS及其分析中心能够提供高精度卫星钟差改正信息,但其具有滞后性,一般要13 d后才能获取。基于此,在讨论灰色系统建模的基础上,利用12 d的IGS钟差文件进行GM(1,1)建模与预报,并将其结果与二次多项式的预报结果进行比较分析,同时对Rb钟和Cs钟的GM(1,1)模型预报效果进行讨论,得出一些有益的结论。
关键词:IGS精密钟差;灰色系统模型;二次多项式;钟差预报;精度
中图分类号:P228.4文献标志码:A
收稿日期:2014-03-31
基金项目:贵州省科技计划资助项目[黔科合GY字〔2011〕3054]
作者简介:潘绍林(1986-),男,硕士研究生.
Prediction of IGS accurate clock error based on grey system model
PAN Shao-lin,ZHANG Xian-yun,DU Ning,FAN Xu-liang,ZHANG Jun
(College of Mining,Guizhou University,Guiyang 550025,China)
Abstract:Clock error is an important error source in precise point positioning,for which IGS and its analysis center can provide satellite clock error correction information of high precision,but it has hysteretic nature that will take 13 days to get the information generally. On the basis of discussing the grey system model,using 12 days’ of IGS clock error file to model and predicting for GM(1,1),its results are compared with those of the quadratic polynomial,as well as the Rb clocks and Cs clocks GM (1,1) model prediction effects are discussed. Some useful conclusions are drawn.
Key words:IGS accurate clock error;grey system model;quadratic polynomial;clock error predicting;precision

钟差是精密单点定位中的重要误差源。为改善GPS精密单点定位的精度,必须实时获取高精度的精密钟差。IGS及其分析中心能够提供高精度卫星钟差,且精度可达0.1~0.2 ns[1-2],但其一般要在13 d后才能获取,不能满足实时精密单点定位的需要。因此,为改善精密单点定位的精度,有必要建立适宜的数学模型,对IGS精密钟差进行预报。卫星钟[3-5]钟差易受外界因素的影响,且有的因素很难掌握其影响规律。而灰色系统理论[6-7]提供了贫信息下建模的新途径,它无需知道原始序列的先验特征,只需通过对原始序列进行有限次数的生成,便可将原本无规则的序列转化为有规则序列,从而为原始序列的高精度预报提供了可能。因此,本文在介绍GM(1,1)模型建模原理的基础上,针对不同类型的GPS卫星钟,分别选择1颗 GPS卫星进行GM(1,1)建模及预报,并将其预报结果与传统的二次多项式模型预报效果进行了比较分析。
1灰色GM(1,1)模型
1.1 GM(1,1)模型建模
设原始序列为如下非负离散数列
(1)
式中n为序列长度。为增强原始序列规律性,对x(0)进行一次累加生成,得生成序列
(2)
对此生成序列建立一阶微分方程
(3)

(4)
式中:

(5)

(6)
1.2 GM(1,1)模型精度评定
模型精度刻画了所建模型对原始序列的拟合程度,其评定的方法有残差大小检验、关联度检验和后验差检验3种。灰色模型的精度通常采用后验差方法进行检验,后验方差比值C和小误差概率P共同评定。一般 C越小越好,且P越大模型的精度就越高。后验方差比值C和P计算方法如下[8]:
设由GM(1,1)模型得还原序列为
根据原始序列及还原序列计算残差
(7)

(8)
(9)
根据S1及S2可得后验比值
由式(7)可得小误差概率
在计算出C,P后,模型精度等级=max{P所在的级别,C所在的级别},其中C,P所在的级别可根据表1确定。
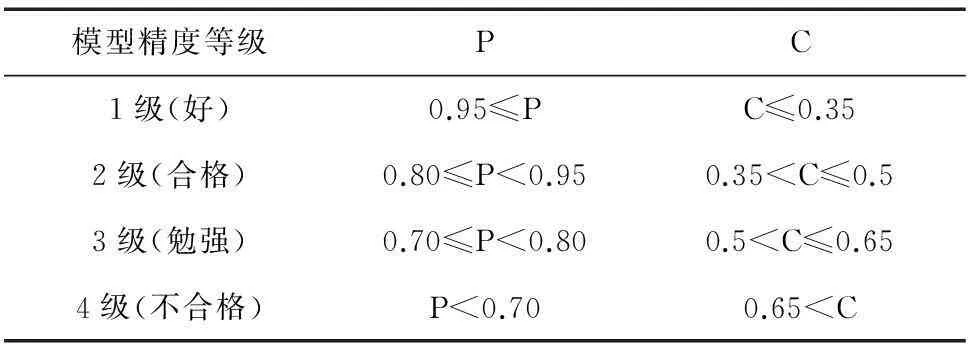
表1 模型精度等级
2算例分析
为比较不同类型卫星上Rb钟和Cs钟的建模精度及预报效果,此处分别选取2012年9月9日至2012年9月20日IGS提供的采样率为5min的PRN01(BlockIIFRb)、PRN10(BlockIIACs)、PRN23(BlockIIRRb)、PRN31(BlockIIR-MRb)、PRN32(BlockIIARb)精密钟差数据,采用如下4种方案进行GM(1,1)和二次多项式模型(PM)建模,并进行钟差的预报与分析。
方案1:以2012年9月9日的钟差数据进行建模与预报,预报2012年9月10日的钟差,并将预报结果与已知钟差进行比较;
方案2:以2012年9月9日的钟差数据进行建模与预报,预报2012年9月10日~15日的钟差,并将预报结果与已知钟差进行比较;
方案3:以2012年9月9日~14日的钟差数据进行建模与预报,预报2012年9月15日的钟差,并将预报结果与已知钟差进行比较;
方案4:以2012年9月9日~14日的钟差数据进行建模与预报,预报2012年9月15日~20日的钟差,并将预报结果与已知钟差进行比较。
2.1 模型的建立
GM(1,1)模型和二次多项式模型以1d、6d的钟差数据建模的拟合精度如表2所示。
由表2可以得出:
1)二次多项式模型和GM模型拟合精度都很高,均达到了纳秒级;
2)采用1d的钟差数据建模时,二次多项式模型和GM模型的拟合精度相当;
3)采用6d的钟差数据建模时,二次多项式模型的拟合精度高于GM模型的拟合精度;
4)不同类型卫星钟模型拟合精度不同,拟合精度由高到低排序依次为:PRN01、PRN31、PRN23、PRN32、PRN10。
2.2 钟差预报
GM(1,1)模型和二次多项式模型预报结果如图1~图5所示,4种方案下GM(1,1)模型预报精度对比结果如表3所示。

表2 GM(1,1)模型和二次多项式模型1 d、6 d的拟合参数及均方根

图1 PRN01的预报残差
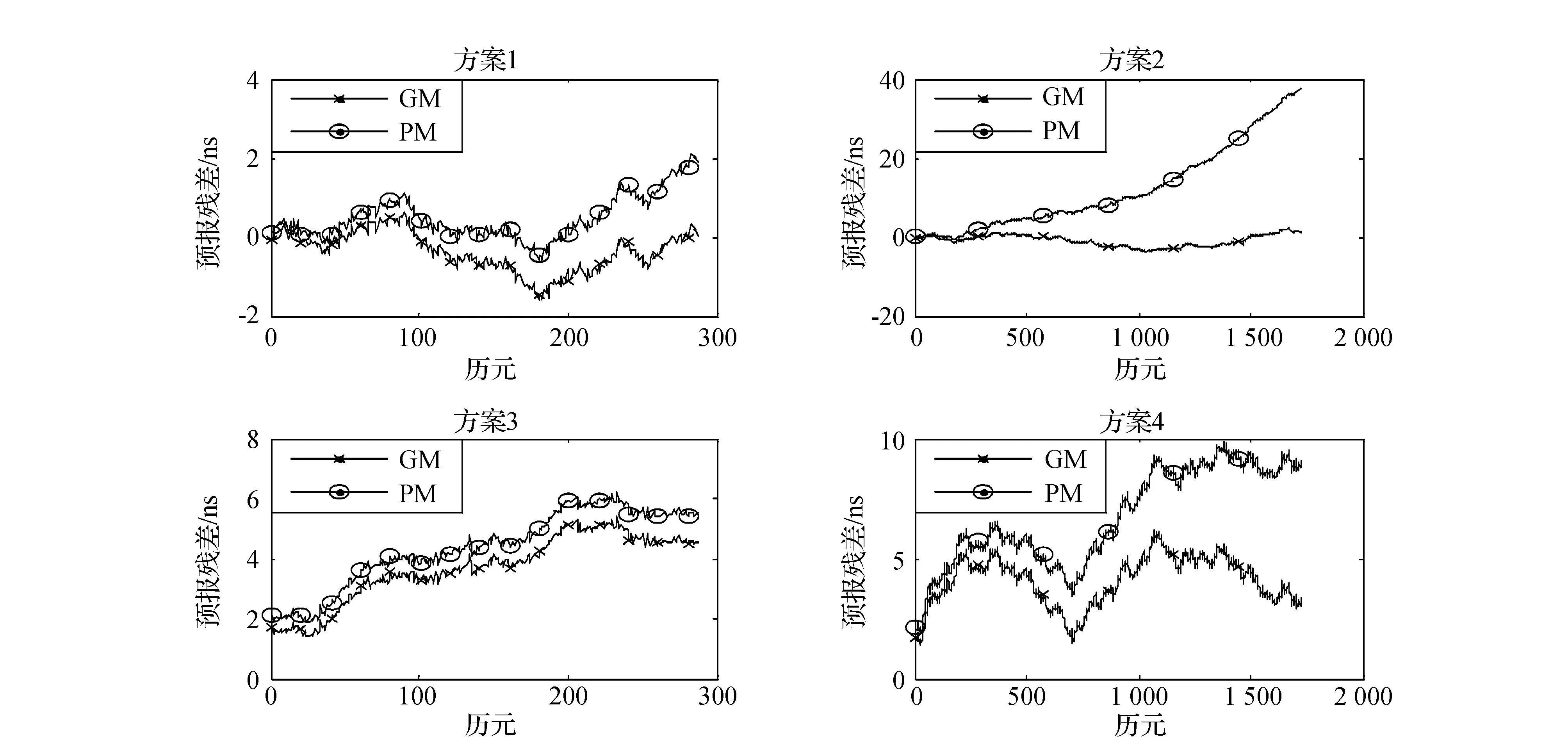
图2 PRN31的预报残差

图3 PRN23的预报残差

图4 PRN32的预报残差

图5 PRN10的预报残差
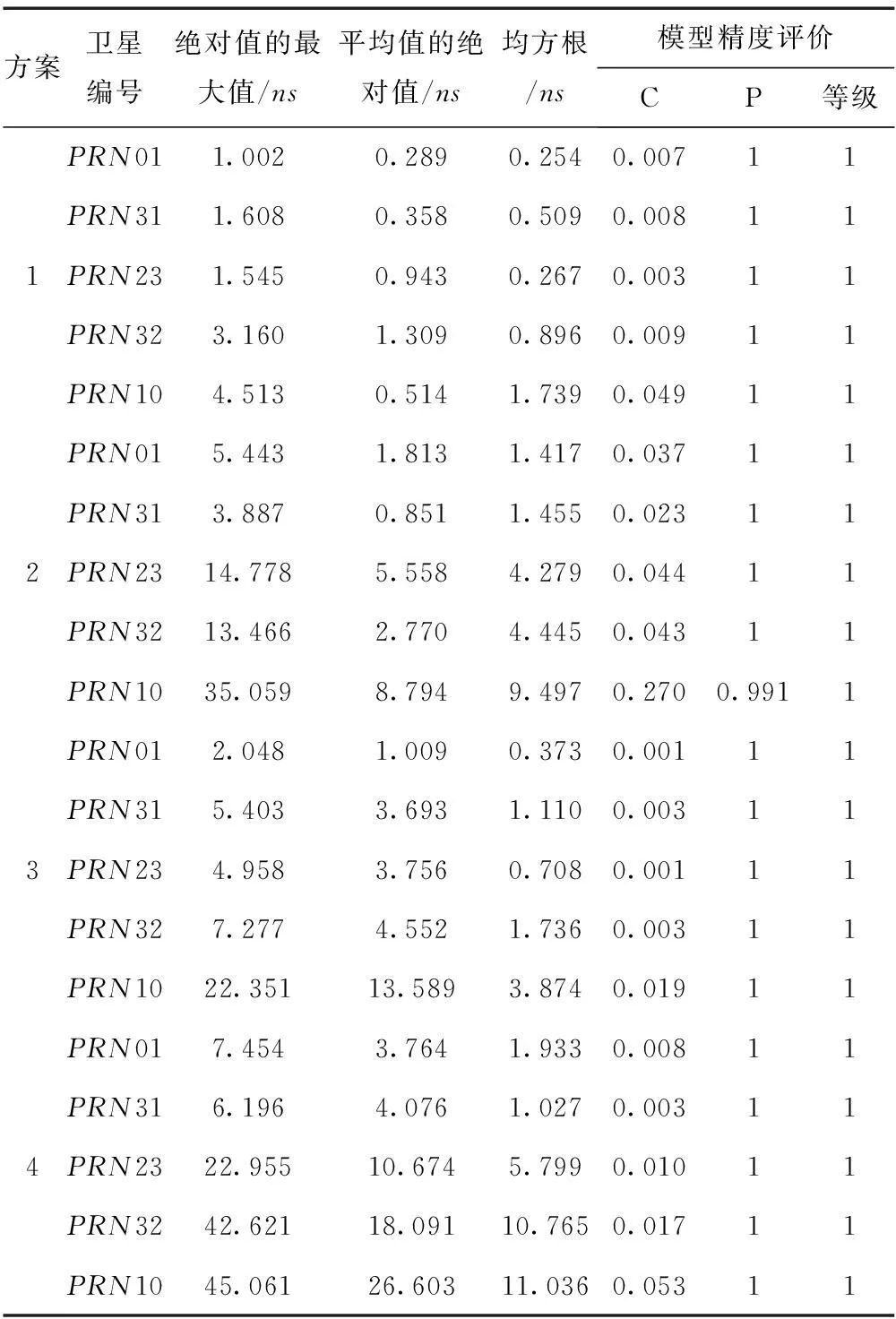
方案卫星编号绝对值的最大值/ns平均值的绝对值/ns均方根/ns模型精度评价CP等级PRN011.0020.2890.2540.00711PRN311.6080.3580.5090.008111PRN231.5450.9430.2670.00311PRN323.1601.3090.8960.00911PRN104.5130.5141.7390.04911PRN015.4431.8131.4170.03711PRN313.8870.8511.4550.023112PRN2314.7785.5584.2790.04411PRN3213.4662.7704.4450.04311PRN1035.0598.7949.4970.2700.9911PRN012.0481.0090.3730.00111PRN315.4033.6931.1100.003113PRN234.9583.7560.7080.00111PRN327.2774.5521.7360.00311PRN1022.35113.5893.8740.01911PRN017.4543.7641.9330.00811PRN316.1964.0761.0270.003114PRN2322.95510.6745.7990.01011PRN3242.62118.09110.7650.01711PRN1045.06126.60311.0360.05311
由图1~图5和表3可以得出:
1)采用1d钟差数据建模时,无论是短期预报还是中长期预报,二次多项式模型预报精度均低于GM(1,1)模型的预报精度,这说明GM模型在“贫信息”下的建模及动态预报更具优越性。
2)采用6d钟差数据建模预测时,二次多项式模型预报精度高于GM(1,1)模型预报精度(卫星PRN31相反);这是由于灰色模型建模所需数据少,并非原始数据越多,预报精度就越高,而二次多项式模型建模所需数据量大,所以数据量足够大时,二次多项式模型具一定的优势;结合PRN31的预报结果,说明预报精度不仅与模型有关,而且与卫星钟类型有关,且不同钟类型的卫星的所建模型数据不一样。
3)对于不同类型的GPS卫星钟,GM(1,1)模型预报的精度不同。预报时长为1d时,PRN01的精度最高、其次是PRN31,精度最差的是PRN10,且PRN10的精度比PRN23、PRN31、PRN32低2~3倍。预报时长为6d时,PRN01精度也最高,PRN31 与PRN23 相当,优于PRN32,PRN10精度同样最差。
3结论
综合以上分析,得出以下结论:
1)无论是二次多项式模型还是灰色模型,随着预报时长的增加,预测结果与实测结果差距越来越大,精度均呈现出降低趋势。
2)进行短期或中长期预报时,如果只有少量的钟差数据,采用GM(1,1)模型预报较好,精度到达纳秒级。如果具有充足的钟差数据,采用二次多项式模型较好,精度可以达到亚纳秒级。
3)GM(1,1)模型预测的精度与卫星钟的类型有关,而且精度的高低顺序为:BlockIIFRb、BlockIIR-MRb、BlockIIRRb、BlockIIARb、BlockIIACs,Rb钟的精度比Cs钟的高2~3倍。
参考文献:
[1]楼益栋,刘万科,张小红.GPS卫星星历的精度分析[J].测绘信息与工程,2003,28(6):4-6.
[2]黄观文,张勤,许国昌,等.基于频谱分析的IGS精密星历钟差精度分析研究[J].武汉大学学报:信息科学版,2008,33(5):496-499.
[3]黄观文,张勤,王继刚.GPS卫星钟差的估计与预报研究[J].大地测量与地球动力学,2009,29(6):118-122.
[4]郑作亚,陈永奇,卢秀山.灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J].天文学报,2008,49(3):306-320.
[5]李玮,程鹏飞,秘金钟.灰色系统模型在卫星钟差短期预报中的应用[J].测绘通报,2009(5):32-35.
[6]崔先强,焦文海.灰色系统模型在钟差预报中的应用[J].武汉大学学报:信息科学版,2005,30(5):447-450.
[7]杨富春,黄张裕,贾莹媛,等.基于GM(1,1)灰色模型卫星钟差短期预报的精度分析[J].测绘工程,2012,21(5):25-29.
[8]黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2010.
[9]邹兵,陈西宏,薛伦生,等.果蝇优化算法优化灰色神经网络的卫星钟差预报[J].测绘科学,2014,39(9):44-48.
[责任编辑:刘文霞]

