抗差估计在多站多星卡尔曼滤波精密定轨中的应用

抗差估计在多站多星卡尔曼滤波精密定轨中的应用

祖安然，宋力杰，王琰

(信息工程大学地理空间信息学院，河南郑州450000)

摘要：针对在多站多星卡尔曼滤波定轨中，粗差探测判断标准选择不合适时会影响卡尔曼滤波解精度的问题，采用放宽粗差探测阈值并在滤波阶段采用抗差估计的方法来控制滤波的精度。利用IGS站和BD站的观测数据，分别计算了GPS、BD卫星单天弧度的定轨结果，并与IGS精密星历、武大精密星历作比较。结果表明，利用抗差卡尔曼滤波方法轨道精度得到了提高。

关键词：卡尔曼滤波；多站多星；定轨；抗差估计；BD

中图分类号：P228文献标志码：A

收稿日期：2014-01-13

作者简介：祖安然(1991-)，男，硕士研究生.

Application of robust estimation in precision orbit determination by using kalman filtering with multi-stations and multi-satellites

ZU An-ran，SONG Li-jie，WANG Yan

(College of Surveying and Mapping，Information Engineering University，Zhengzhou 450000,China)

Abstract：As for the Kalman filtering precision orbit determination with multi-stations and multi-satellites，the inappropriate choice of outlier detection criterion will affect Kalman filtering precision.The relaxation of the outlier detection threshold and the robust estimation method in filtering stage shall be used to control the filter precision.Using GPS and BD station observation data,GPS and BD satellite orbit results of single day radian are calculated, compared with the precise ephemeris,Wuda precise ephemeris.The results show that the precision of orbit with robust Kalman filter method is improved.

Key words：Kalman filtering;orbit determination;robust estimation;BD

在卫星动态模型准确的情况下，当地面站观测数据中仅含有偶然误差，采用扩展卡尔曼滤波方法可得到每个历元的可靠解。但在实际观测中，由于各方面的影响观测数据不可避免地含有粗差，因此在数据预处理阶段，需要综合利用多种粗差探测的方法来剔除粗差。在卫星观测数据处理中，常用的粗差探测方法有MW组合、LC-PC组合等。在粗差探测时需要人为地设定判断标准，但对于残差在阈值附近的观测值是否判定为粗差仍未得到很好解决。过于严格的阈值，可能会将某些好的观测值当成粗差处理，历元观测值个数也会减少；过于宽松的阈值会使粗差不能完全被剔除。这两种方法有时都会影响解的精度。对于类似的问题，王潜心等在动态相对定位中采用抗差最小二乘配合粗差探测的方法来解决[1]。文援兰对抗差估计在精密定轨中的应用做了研究[2]。而抗差估计随着权函数的不同对应着不同的估计方法。常用的权函数有Huber权函数、Tukey权函数、李德仁权函数、IGG权函数等。李浩军等曾对各种不同的权函数进行了分类和对比分析，结果表明具有正常段、可疑段和淘汰段的IGG权函数更加稳定一些[3]。本文在数据预处理阶段放宽粗差探测条件，在滤波阶段使用杨元喜等提出的IGG3权函数[4]来进行抗差估计，控制残差较大的观测值，并通过实测的GPS、BD观测数据进行了验证。

1粗差探测分析

在数据预处理阶段采用MW组合和LC-PC组合来剔除粗差。

MW组合的探测统计量为

(1)

LC-PC组合的探测统计量为

(2)

采用2011年10月27日全球25个IGS站的观测数据，以四倍方差为限差得到的每个历元观测值数作为标准，分别统计取二倍方差、三倍方差为限差时历元观测值减少量的最大、最小百分比，结果如表1所示。

表1　减小限差历元观测量减少比例　%

由表1可以看出，当严格粗差探测的判断标准时，会减少历元的观测量个数，有时可以达到接近20%，当观测条件不好的时候会更多。其中删减的观测值包括含有小粗差的，也包括观测噪声接近于限差的。在现代高精度要求的条件下，合理充分地利用观测量是有切实必要的，而抗差估计可以解决这个问题。

2多站多星抗差卡尔曼滤波原理

以300 s的计算间隔将数据分隔成若干历元，在同一历元内以消电离层载波组合作为观测量，历元内所有测站对应相应卫星的观测量组成观测方程，其误差方程式为

(3)

其中:N为消电离层组合模糊度，为浮点解，作为参数进行估计；δtr,δts分别为接收机钟差和卫星钟钟差，也作为参数进行估计；δtro为对流层延迟改正，本文采用Saastamoinen模型[5]计算，并将湿分量系数、南北方向水平梯度和东西方向水平梯度作为参数进行估计；δtide为地球潮汐改正；δrel为相对论效应改正；δpha为天线相位缠绕改正，这3项可由公式直接进行改正。卫星位置、速度、光压参数包含在理论距离ρ中，需要对ρ做线性化处理。因此，误差方程的参数包括卫星位置、速度、光压参数、模糊度、接收机钟差、卫星钟差以及对流层参数。

根据文献[6]对卫星进行摄动力分析，其二阶微分动力学方程为

(4)

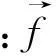
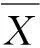
(5)

(6)

(7)

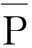
IGG3法的权函数为

(8)

其中:k0取值一般为1.0～1.5，k1为2.5～3.0[4]。

3计算结果与分析

在IGS网站下载25个测站2011年10月27日的观测数据，同时下载广播星历文件和sp3精密星历文件。采用以上数据以及武汉大学提供的2012年11月5日18个BD跟踪站的观测数据、广播星历和精密星历进行以下算例分析。

3.1　全球站GPS单天定轨结果

利用25个全球分布IGS跟踪站，以广播星历计算的300 s间隔的坐标值进行最小二乘拟合的初始历元15参数作为初始先验值，进行不同阈值的单天弧长卡尔曼滤波和抗差卡尔曼滤波轨道计算。计算时进行二次滤波即前向滤波和后向平滑，以后向平滑值为最终结果。将轨道结果进行积分后与精密星历进行比较，统计27日28颗卫星3个方向的均方差及3DRMS值，结果见图1～图3。

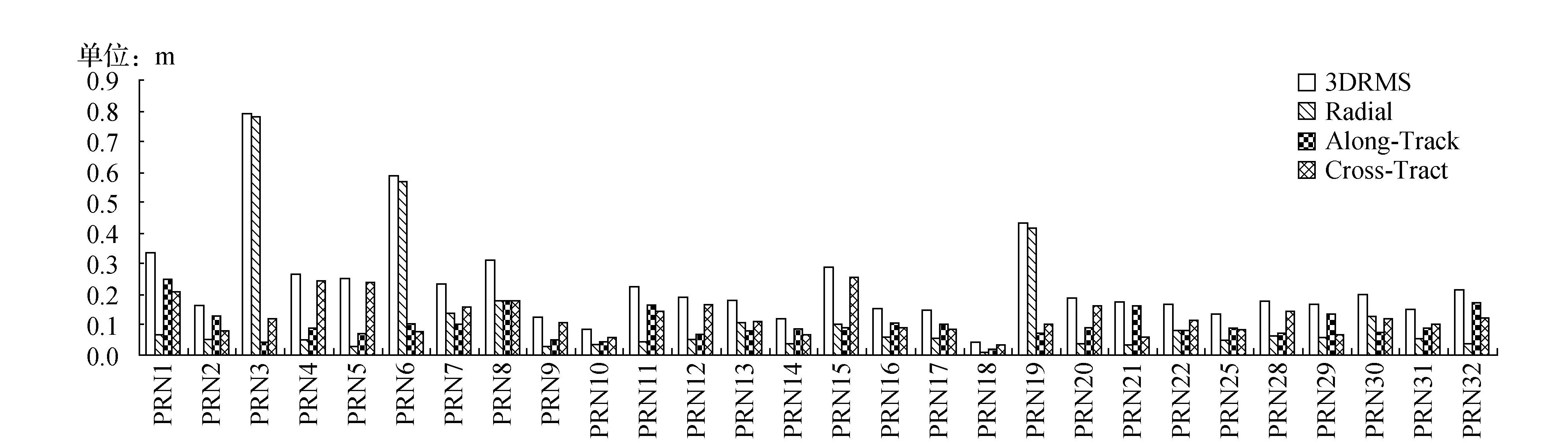
图1　以2倍中误差为限差的25站卡尔曼滤波结果与精密星历之差

图2　以4倍中误差为限差的25站卡尔曼滤波结果与精密星历之差

图3　以4倍中误差为限差的25站抗差卡尔曼滤波结果与精密星历之差

从图1～图3可以看出，少数卫星以2倍中误差为限差比以4倍中误差为限差得到的卡尔曼滤波结果精度略高一点，其余大部分卫星两种结果精度都基本相同；而在以4倍中误差为限差的基础上采用抗差卡尔曼滤波得到的结果整体上要比前两种的都要好，特别是对于PRN03号而言，均方根误差直接从0.8 m降到了0.5 m。

3.2　区域站BD单天定轨结果

利用区域分布18个BD跟踪站，以广播星历计算的300 s间隔的坐标值进行最小二乘拟合的初始历元15参数作为初始先验值，进行不同阈值的单天弧长卡尔曼滤波和抗差卡尔曼滤波轨道计算。计算时进行二次滤波即前向滤波和后向平滑，以后向平滑值为最终结果。将轨道结果进行积分后与武

大精密星历进行对比，统计8颗卫星单天3个方向的均方差及3DRMS值，结果见图4～图6。

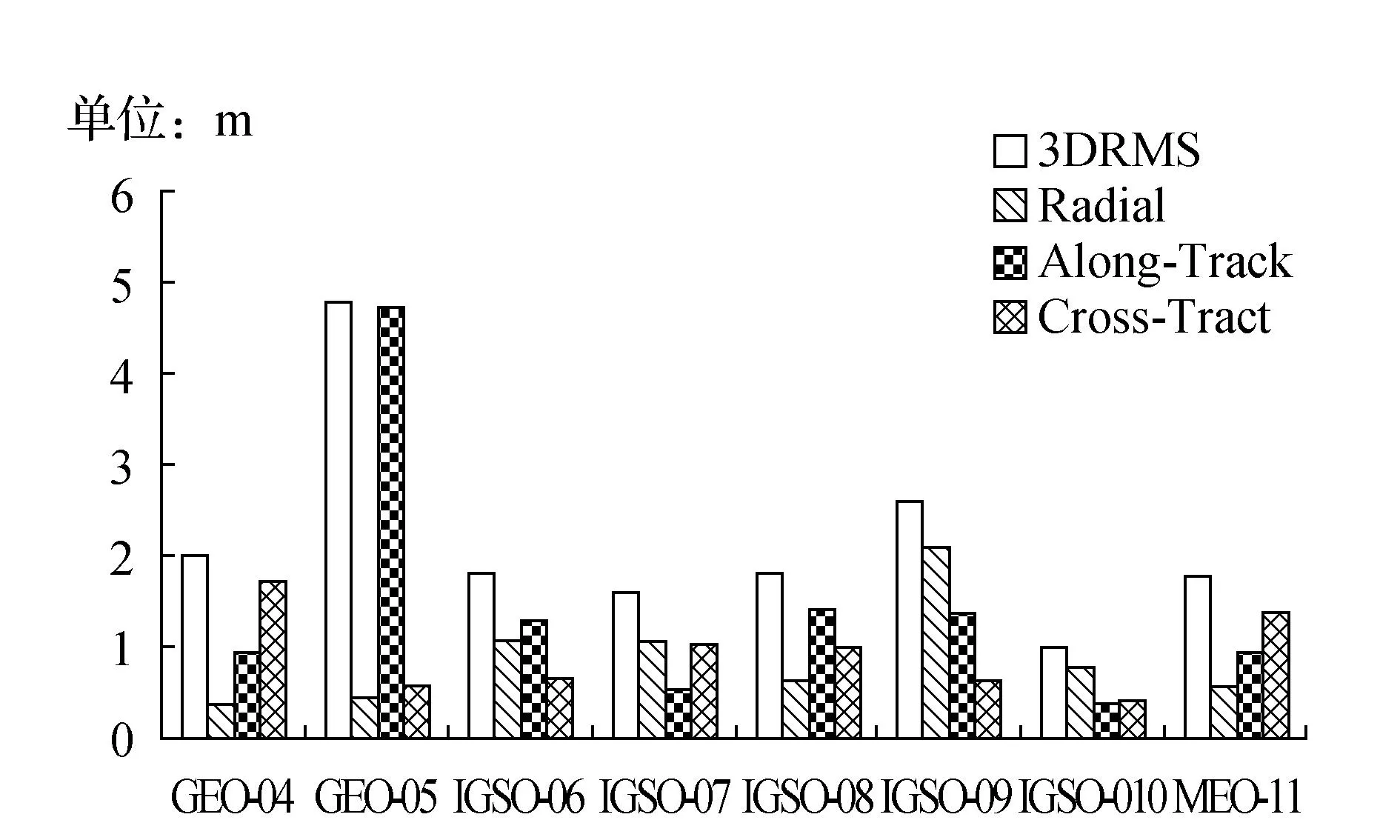
图5　以4倍中误差为限差的18站卡尔曼滤波结果与 精密星历之差

图6　以4倍中误差为限差的18站抗差卡尔曼滤波 结果与精密星历之差

从图4～图6可以看出，5号GEO卫星和11号MEO卫星以2倍中误差为限差的得到的卡尔曼滤波结果要比以4倍中误差为限差得到的结果差，其它卫星两种结果基本相同。在以4倍中误差为限差

的基础上采用抗差卡尔曼滤波的方法使5号GEO卫星和11号MEO卫星的精度又得到了进一步提升，其它卫星结果与前两种方法基本相同。总体上来看采用抗差估计得到的结果整体上要比前两种的都要好。

4结束语

在数据粗差探测时，要人为地设定判断标准，阈值的大小直接决定了历元观测值的数量和质量。阈值设定的不合适，很可能会使卡尔曼滤波的解受到影响。而在放宽阈值的情况下采用抗差卡尔曼滤波很好地解决了这个问题。抗差卡尔曼滤波能够充分利用观测数据，使轨道精度得到一定的提高。这对我国北斗卫星精密定轨也具有一定的借鉴意义。但抗差卡尔曼滤波计算时需要重复迭代，其计算效率要比卡尔曼滤波的低。

参考文献：

[1]王潜心，徐天河，许国昌.粗差探测与抗差估计相结合的方法在动态相对定位中应用[J].武汉大学学报：信息科学版，2011，36(4):476-480.

[2]文援兰.航天器精密轨道抗差估计理论与应用的研究[D].郑州：信息工程大学，2001.

[3]李浩军，唐诗华，黄杰.经典选权迭代法与两步抗差估计的提出[J].海洋测绘，2007，27(1):17-20.

[4]YANG Y，CHENG M K，SHUM C K，et al.Robust Estimation of Systematic Errors of Satellite LaserRanger[J].Journal of Geodesy，1999，73(7):345-349.

[5]WU J T，WU S C，HAJJ G A .Effects of antenna orientation on GPS carrier phase[M].Manuscripta Geodaetic，1993.

[6]王琰，宋力杰，黄令勇.GPS卫星精密定轨中的摄动力分析[J].测绘工程，2013，22(6):16-20.

[7]陈宪东，黄丁发.GPS卫星定轨中的摄动力影响分析[J].测绘科学，2006，31(6):72-73.

[8]SPRINGER T A，BEUTLER G，ROTHACHER M.A new Solar Radiation Pressure Model for the GPS Satellites[J].CODE IGS Analysis Center Technical Report,1999,673.

[9]杨元喜.自适应动态导航定位[M].北京：测绘出版社，2006:121-126.

[10]蒋廷臣，张月莲.集合卡尔曼滤波的GPS周跳探测[J].测绘科学，2014，39(9)：11-13.

[责任编辑：刘文霞]