关于运算意义构建的思考


俞正强,浙江省小学数学特级教师,北京师范大学教育家书院兼职研究员,浙江师范大学硕士生导师,浙江省金华师范学校附属小学校长。
小学数学中的运算主要有加、减、乘、除四种。目前,我们对加、减、乘、除这四种运算的定义基本上是这样的:加法,将两个数合并成一个数的运算叫加法;减法,已知两个数的和与其中一个加数,求另一个加数的运算叫减法;乘法,求几个相同加数和的简便运算;除法,已知两个因数的积与其中一个因数,求另一个因数的运算。
从这些运算定义来看,加法是所有运算的源头。减法是依据加法来定义的,是加法的逆运算;乘法也是依据加法来定义的,是加法的简便运算;除法是乘法的
逆运算。
由此看来,所有的运算在本质上都是加法。
那么,这样的定义合理吗?
一、意义构建的两种基本样式
我在《小学数学概念教学的两种基本样式》一文中,对概念的意义构建做过
分类。
类型一:概念本身能够在生活中找到原型。学生在生活中因为对原型的经历,已经具备该概念所包含的内涵和外延的理解。我们把这种概念的意义构建表述为:
类型二:概念本身在生活中找不到原型。学生在生活中没有关于该概念的任何经历。我们把这种概念的意义构建表述为:
按照这两种分类考察我们对运算意义的定义,应该属于第二种:将学生视为空白定义运算意义。先定义一个加法,再以加法为标准,定义减、乘、除,形成小学阶段的运算系统。这样的意义构建合理吗?
二、加、减、乘、除的运算原型
加、减、乘、除在生活中是各有原型的。生活中的所有运算可分为两类:分与合。这两种运算用政治语言来表达即统一与分裂,用物理语言可以描述为聚与裂,用伦理语言可描述为结婚与离婚等,用数学语言来表述就是加与减。
由部分而为整的,我们称之为合,即加。由整而为部分的,我们称之为分,即减。生活中,是先有分还是先有合?若先有合,那部分从何而来?若先有分,那整体又从何而来?因此,分与合可以转化,却不可从属。分与合是独立而又彼此相通的两种运算。合久必分,分久必合。合就是合,分就是分。
何为合,何为分?学生在生活中已经有了充分的认识,绝不会混淆。那“比”是“分”,还是“合”呢?
生活中有许多关于“比”的原型。就“境”而言,“比”应该属于分,即把一个比较物分为另一比较物与比余部分。
讨论完加与减之后,再来讨论乘和除,乘、除有原型吗?
生活中的运算分为分与合,这个世界是秩序井然的,是赋予生命以安全感的,那这种秩序井然与安全感是怎么来的呢?因为世界的分与合充满规律,这种规律性表现在运算上就是等合与等分。
什么是等合?比如,今天合进来的一天有24小时,明天合进来的一天也是24小时,不会突然变成2小时。这种等合是世界有序与安全的原因。这种等合原型,生活中比比皆是,将此种原型定义为乘法。
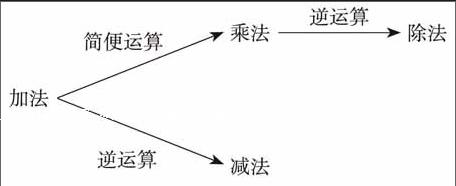
那么等分呢?这种分法当然就更普遍了,我们将等分定义为除法。除法首先是独立于乘法而存在的一种运算,其次是可以与乘法相转化的一种运算。如果这一认识成立,那小学数学的运算体系可以描
述为:
三、为什么要讨论这个问题
我们为什么要讨论加、减、乘、除的意义构建呢?我们先来分析一个案例。
小学一年级数学教师都有一种纠结,这个纠结来自以下类型的题目。
这幅图用一个算式来表示,正确的算式是:
但学生很喜欢用下列算式来表示:
教师怎么跟学生讲也讲不明白,结果是,现在许多地方在改革的旗帜下变成这样的题目:
让学生填出三个算式:
5-2=3
5-3=2
2+ 3=5
教师千万不要小看这种对题目题意的随意给学生数学学习带来的伤害,造成这种困顿的原因来自我们对运算意义构建的不合理。
现在,我们看这幅图。就图境而言,是在分还是在合?显然,所有学生会认为这是一个“分”境,飞走两只天鹅,飞走了,用减法。但就量而言,是两个部分,即飞的部分与不飞的部分,这两部分在同一幅画中,自然要用加法。
而小学数学加法的运算意义正是基于量的判断而建立起来的,学生正是用我们所教的意义来认识的。因此,我们教学中遇到问题,没有真正认识问题,而是用一种和稀泥的方法掩盖过去,美其名曰“一题多解”,是一件十分有后患的事情。
四、意义,问题解决的审题抓手
课改之前,我们叫解应用题,课改之后,我们叫问题解决。课改之前,我们教学生解应用题,总是先让学生熟背数量关系式,也叫关系等式。例如,部分数+部分数=总数、大数–小数=相差数。运用关系等式,用综合法与分析法来解决应用题。
(2)班采摘15千克,(3)班采摘20千克,一共采摘多少千克?
分析法:
综合法:
在课程改革时,认为这样做比较难,放弃关系等式,不再使用分析法与综合法。教师认为没法教,因为没有抓手,于是还是偷偷地用老办法。
各个版本的教材在修订时,似乎关系等式又有所出现,但出现得不尽兴,教师摸不清是什么意图,于是又按自己的老方法教学。
其实,解决问题不用数量关系不要紧,数量关系是建筑于相应运算意义的建构之上的,我们不用数量关系就要相应地改变运算意义的建构。再举个例子,不同的意义建构会带来不同的审题过程。
两个班共采摘35千克,(1)班采摘15千克,问(2)班采摘多少千克?
版本1:读题,已知总数和部分数,求另一个部分数,用减法。
列式:35-15=
版本2:读题,这是一个“合”境,用加法。
列式:15+〇=35
这就是两种不同的意义构建带来的不同审题。
五、结语
加、减、乘、除是对生活原型的定义,而问题解决的情境就是一个理想化的原型。只有运算意义符合生活原型时,它才会成为问题解决的审题基础。
(责任编辑:孙建辉)

