改进的Mumford-Shah模型及其在图像恢复和分割中的应用
改进的Mumford-Shah模型及其在图像恢复和分割中的应用
毕翔,豆泽阳,李浩
(中国传媒大学 理学院,北京 100024)
摘要:在本文中,我们讨论了几个在图像恢复和图像分割中的经典泛函,并且我们用非凸泛函去近似它们。这些经典泛函和两个变量相关u、v,其中u是图像本身,v是它的边缘。这样的话,这个问题就包含着两个方程和两个未知变量,而在我们的近似非凸泛函中,只需要解关于u的一个单变量系统,因为我们引入了趋近于0的参数ρ,把v表示成了一个关于u的梯度的函数。我们还讨论了这些近似模型关于时间的演化方程。最后,在我们的数值实验中,计算了p=1的情况。我们发现算法不但很快,而且也可以很好地保留边缘。
关键词:图像恢复和分割;偏微分方程;欧拉方程;非凸泛函
中图分类号:O241.82文献标识码:A
收稿日期:2014-12-26
作者简介:毕翔(1991-),男(汉族),江苏淮安人,中国传媒大学硕士研究生.E-mail:bixiang@cuc.edu.cn题的最终解。变分法研究的对象是泛函极值问题,而变分欧拉方程可以利用曲线演化的偏微分方程来逼近。
TheReducedMumford-ShahModelandItsApplicationsin
ImageRecoveryandSegmentation
BIXiang,DOUZe-yang,LIHao
(SchoolofScience,CommunicationUniversityofChina,Beijing100024)
Abstract:In this paper,we discuss several classical functionals in image recovery and segmentation.Moreover,we approximate them by nonconvex functional.These classical functionals are related to two variables u and v,where u is the image function and v is another variable which allows to detect the contours.Then this question consists in two equations and two unknowns,while in our approximate nonconvex functional,we only need to solve a system about one variable u.Because we introduce a parameter ρ,which goes to zero.Then we could express v as a function of the gradient of u .We also discuss the evolution equation of these models about time.Finally,in our numerical experiment,we compute the model in the case p=1 and find that not only the algorithms are faster but also the edges are very-well preserved.
Keywords:image recovery and segmentation;partial differential equation;Euler equation;nonconvex functional
1引言
在图像分析领域,图像去噪和分割是两个非常重要的问题。图像分割对于图像目标的特征提取和表达具有重要的意义。一般的问题是这样的:对于给定的一幅带有噪声的图像,我们需要在对其去噪的基础上提取出它的边缘。
基于偏微分方程的图像分割方法是将图像分割问题转化为能量泛函的极小化问题,并用变分法寻求问
本文通过对经典的Mumford-Shah模型的近似模型做简化,将原来的双变量系统变为单变量系统,从而使得算法更快并且能够很好地保留边缘。
2预备知识
2.1 偏微分方程的基本概念及其差分格式
如果一个微分方程中,自变量的个数为两个或者两个以上,那么我们称之为偏微分方程(partialdifferentialequation,PDE),PDE的阶次即为方程中阶次最高的偏导数的次数。
在图像处理中常用到的是偏微分方程中的椭圆形方程和抛物型方程。椭圆形方程是指方程中只包含对空间变量的偏导数的偏微分方程。泊松方程:
是典型的椭圆形方程。抛物型方程中不仅包含对空间的偏导数,还包含对时间的偏导数。热传导方程:
是典型的抛物型方程。
常用的PDE数值计算方法有:有限元法、有限差分法和谱法[1]。在图像处理中,有限差分法用的比较多。有限差分的基本思想是用相距有限距离的两个邻点函数值的差与两点间距离的比值来近似函数对变量的偏导数。一般情况下,我们会用向前差分来近似对时间的偏导数:

在空间中,对x的一阶偏导数的近似,我们通常使用以下三种差分格式。
向前差分:

向后差分:

中心差分:

对于二阶偏导数,我们只需在一阶偏导数的基础上再做一次近似即可。通过近似,我们就可以把偏微分方程转化为一个代数方程,从而选定数值方案进行计算了。数值方案分为显式、隐式和半隐式三种。从显式到半隐式再到隐式,格式会越来越稳定,但是实现起来也会越来越困难。因此,经常会选择稳定性较好且实现较容易的半隐式格式方案。
2.2 变分原理
泛函的求极值问题成为变分问题。基于偏微分方程的图像去噪及图像分割问题,通常最终会归结于求一个能量泛函的极小值问题。在一维情况下,能量泛函可能有如下形式:

(1)
由于扰动v在边界上的值v(x0)=v(x1)=0,所以有u(x0)+v(x0)=a,u(x1)+v(x1)=b。根据分布积分法:
代入(1)式得:
(2)
在二维情况下,能量泛函的形式为E(u)=∫∫F(x,y,u,ux,uy)dxdy,其Euler方程的推导类似,结果为:
2.3 梯度下降流
一般情况下,上述Euler方程会是一个非线性PDE,离散之后的计算比较困难。我们可引入一个时间辅助变量,将椭圆型方程转化为抛物型方程,将静态问题转化为动态问题。当方程随着时间演化达到稳态时,得出的u便是该变分问题的解。


那么E(u)就会不断减小。
3主要模型及推导
3.1 Mumford- Shah及其近似模型
在图像恢复和分割领域有一个的模型——Mumford-Shah模型[2]:
GMS(u)=∫(α|▽u|2+β|u-u0|2dxdy)+H1(su)
(3)
其中,α,β是两个正权值参数。su是u的不连续点构成的跳跃集,即边缘。H1是一维Hausdoff测度。在Rn上,简单曲线的一维Hausdoff测度等价于曲线的长度,由于H1(su)的计算不方便,故后人提出了很多简化的模型。该泛函的第一项为光滑项,保证u在连续区域上的充分光滑。第二项是保真项,保证了分割前后的图像不偏差太大。第三项是边缘长度,保证边缘不致填满整幅图像。
Ambrosio和Tortorelli提出用对偶变量来表征跳跃集su[3],得出:
(4)
现分别对(4)式中的u和v做一阶变分,则有:
(5)

(6)
这样,我们就将原来的双变量系统转化为单变量系统了,从而使算法更加得高效。
Shah根据A-T的这个思想,也提出了一个M-S模型的近似模型[4]:
GS(u,v)=∫
(7)
我们可以利用同样的方法将其变成一个单变量系统:
Gs(u)=∫
(8)
我们将以上两个近似模型统一成[5]:
其中p≥1。在数值实验中,我们用|u-u0|的L2范数代替原来的Lp范数[6],计算以下模型:
Gρ(u)=∫
(9)
3.2 模型的离散化
(8)式中的Euler方程为
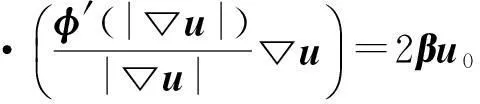
(10)

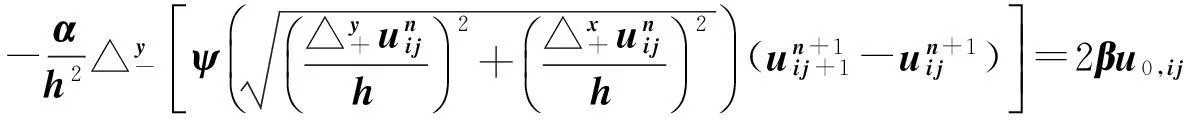
再将外层的差分展开:
其中:



故

若加入梯度下降流[8],则演化模型为:

则:
4数值实验
在我们的实验中,我们采用256×256的Lenna彩色图像和 256×256的Camera灰度图像进行实验。采用的噪声是均值为0、方差为0.01的高斯白噪声,效果对比图如图1、图2所示。在图1和图2中,(a)为原始图像,(b)为加噪图像,(c)为恢复后图像,(d)为分割后图像。
在数值实验中,我们采用平均平方误差(meansquareerror,简称MSE)和信噪比(SignaltoNoiseRations,简称SNR)来评估图像恢复的质量。MSE和SNR定义如下:
其中,g(i,j)与f(i,j)分别表示原始图像与恢复后的图像,M、N分别是图像的长和宽。表1给出了两幅图像的最优平均平方误差、信噪比和迭代时间,图3、图4分别反映出了Camera灰度图像的平均平方误差与迭代步数的关系以及信噪比与迭代步数的关系。图5、图6分别反映出了Lenna彩色图像的平均平方误差与迭代步数的关系以及信噪比与迭代步数的关系。
所有实验都是在MATLABR2014a版本上运行的。执行运算的笔记本电脑是Intel(R)Core(TM)i7-4710MQCPU@ 2.50GHz2.50GHz处理器,4.00GB的内存。在解方程组时,使用Gauss-Seidel迭代方法[9]进行迭代,Gauss-Seidel方法是一种不动点迭代,当达到最优解附近时趋于稳定。

表1 半径采样下核磁共振图像重建实验结果

(a)原始图像 (b)加噪图像

(c)恢复后的图像 (d)分割图像 图1

(a)原始图像 (b)加噪图像

(c)恢复后的图像 (d)分割图像 图2

图3 平均平方误差与迭代次数的关系

图4 信噪比与迭代步数的关系

图5 平均平方误差与迭代次数的关系

图6 信噪比与迭代步数的关系
5结论
在本文中,我们基于Mumford-Shah的简化模型,利用对偶变量将原来的双系统变成了单变量系统,并且引入了时间演化模型,使得算法变得更加快速的基础上,依然可以很好地保留边缘。
事实上,我们可以看到,在我们的数值实验中,我们极小化的泛函是一个非凸泛函,这是一个病态问题。但是,我们依然可以看到:在数值实验中,加噪的图像被很好地恢复,而且分割的边缘也比较清晰。因此,我们才可以在非凸问题上有所妥协。然而,对这部分的理论分析以及解释还需要做进一步的分析和研究。
参考文献
[1]FombergB.Thepseudospectralmethod:Comparisonswithfinitedifferencesfortheelasticwaveequation[J].Geophysics,1987,52:483-501.
[2]DMumford,JShah.OptimalApproximationsbyPiecewiseSmoothFunctionsandAssociatedVariationalProblem[J].CommunicationsonPureandAppliedMathematics,VolXLII(1989),577-685.
[3]AmbrosioL,TortorelliV.Approximationoffunctionalsdependingonjumpsbyellipticfunctionalsvia-convergence[J].CommunicationonPureandAppliedMathematics, 1990,43:999-1036.
[4]JShah.ACommonFrameworkforCurveEvolution,SegmentationandAnisotropicDiffusion[J].ProceedingsofIEEEConferenceonComputervisionandpatternrecognition,SanFrancisco,June,1996,136-142.
[5]ChanT.VariationalImagerestoration&segmentationmodelsandapproximations[OL].http://www.math.ucla.edu/~imagers/htmls/seg.html.
[6]ChanT.Reducednon-convexfunctionalapplicationsforimagerestoration&segmentation[OL].http://www.math.ucla.edu/~imagers/htmls/seg.html.
[7]王桥.数字图像处理[M].北京:科学出版社,2009.
[8]LVese.VariationalproblemsandPDE’sforimageanalysisandcurveevolution[D].PHDThesis,UniversityofNice,Nov,1996.
[9]TimothySauer.NumericalAnalysis[M].NewJersey:PearsonEducationInc,2006.
(责任编辑:宋金宝)

