多层水泥结构吸波材料设计与测量技术研究

多层水泥结构吸波材料设计与测量技术研究

逯贵祯，付子豪，余泽，肖怀宝

(中国传媒大学信息工程学院，北京 100024)

摘要：本文研究一种宽带多层水泥结构的吸波材料。通过在水泥材料中加入不同比例的石墨和铁磁粉末材料，并加工形成具有多层夹心结构的结构吸波材料。为了测量该结构吸波材料的等效电磁参数，我们进一步发展了与测量参考面无关的电磁参数测量方法，提出了一个用于参数提取的非线性方程，与原有的方程相比，该函数的数学性质更好，因而在迭代求解中会提高求解的收敛速度。其次，考虑迭代求解非线性方程过程中初值的选择问题，给出了针对该非线性方程的估计置信区域半径的公式。最后，针对该结构吸波材料进行了测量与等效电磁参数的分析计算，得到了有效介电常数和有效磁导率。

关键词：微波测量；等效介电常数；等效磁导率；结构吸波材料

中图分类号：O441.5文献标识码：A

收稿日期：2014-11-13

基金项目：高等学校博士学科点专项科研基金博导类资助课题

作者简介：逯贵祯(1957-)，男(汉族)，北京人，中国传媒大学教授，博士生导师.E-mail：luguizhen@cuc.edu.cn

The Study in Design & Measuring Technology of Multilayer

Structure Cement Absorbing Material

LU Gui-zhen，FU Zi-hao，YU Ze，XIAO Huai-bao

(Information School，Communication University of China，Beijing 100024，China)

Abstract：This paper discusses a broadband multilayer absorbing materials cement structure.By adding different proportions of graphite and the ferromagnetic material powder in the cement material，thus processed to form a structure absorbing material has a multilayer sandwich structure.Because of the shortcomings in traditional measuring method，we further develop the electromagnetic parameter measurement method that unrelated to reference plane.First，we put forward a nonlinear equation for parameter extraction which compared with the original equation and the mathematical properties of the function are better.So it can improve the convergence speed of solving in the iteration.Secondly，considering the iterative initial value selection problem in the process of solving nonlinear equation ，nonlinear equations is given for the estimation of confidence region radius formula.Finally，in view of the actual cement samples were measured with electromagnetic parameter extraction calculation，the calculation results agree well with the measured results.

Keywords：microwave measurement；equivalent permittivity；equivalent permeability；absorbing materials

1引言

结构吸波材料是由不同结构组合形成的一种能够吸收电磁波的材料，他可以在一定频率范围吸收入射电波，减少电磁波散射。它的主要应用有航空航天，电磁兼容，微波技术等领域。结构吸波材料的工作原理是吸收入射电磁波，达到减少电磁波反射信号的目的。最早的传统形式吸波材料是Salisbury薄屏，其工作原理是在导体表面四分之一波长位置放置一个阻性薄板结构，这样入射电磁波从导体的反射波与阻性薄板反射的电磁波会产生干涉效应，减少反射的电磁波信号。为了进一步增强吸收特性，发展了Jaumann的多个电阻性薄板结构。除了电阻性波板结构，雷达吸波材料可以利用损耗电介质和损耗磁介质组成。损耗电介质通常采用epoxy/fiber复合结构，其中包含有炭黑材料。还有些材料使用碳化硅泡沫。磁损耗材料通常采用基于铁氧体的复合材料。另外还有使用有耗等离子体薄层作为吸波材料。

水泥材料是一种常用的建筑材料，水泥本身对电磁波的吸收是不大的。但是通过在水泥材料中加入一定的添加剂可以提高水泥材料的电磁波吸收率。水泥中的添加剂主要是改变水泥的等效介电常数与磁导率，通过水泥基体中的吸波成分吸收电磁波。目前常用的添加剂有铁氧体材料，金属粉末，石墨，金属丝，金属片等有耗介质。文献[1-5]基本反映了目前国内对各种基于水泥材料的吸波材料研究情况

为了得到需要的基于水泥材料的吸波材料，需要有一个有效可靠的测量方法。双端口传输与反射测量技术是在20世纪70年代建立的电磁参数测量技术。该测量技术(NRW 方法)具有简单准确的优点，是目前测量技术中广泛使用的一种方法[10]。该方法的一个缺点是需要把测量S参数的参考面变换到待测材料的界面。传输系数与反射系数的相位依赖于参考面的选择，所以参考面位置带来的误差会影响测量结果的准确性[11]。1990年，Baker-Jarvis提出了一个与参考面无关的测量方法[12]。在参考面无关的测量方法中，采用迭代算法可以获取材料的介电常数与磁导率参数。由于采用迭代方法，所以一个好的初始猜测是非常必要的。随后出现了相关的文章对这个方法进行改进。文献[13]针对低损耗介质，通过匹配测量散射参数和计算散射参数获取介质的电磁参数。文献[14]提出了利用反射系数幅度测量材料参数的方法。该方法要求材料衰减至少10dB，而且对测量技术有特殊的要求。

本文的研究工作首先在基于水泥吸波材料研究的基础上，设计了一种结构吸波材料，该结构吸波材料具有所需要的低反射性能。为了对该结构的等效电磁参数进行分析研究，针对测量中存在的散射参数相位参考面的误差问题，提出了一个与散射参数相位参考面无关的 非线性方程，用于材料电磁参数的提取。该非线性方程采用迭代方法求解，并且针对迭代方法的初值选取问题，提出了一个确定置信区域半径的公式，该公式有助于选择合理的迭代初值。最后对该结构吸波材料进行了测量研究。测量结果与计算结果符合良好。

2水泥结构吸波材料研究

为了提高水泥材料的吸波性能，通常需要在水泥中加入添加剂。在研究中我们通过加入羰基铁粉来提高水泥中的磁导率，通过加石墨提高水泥中的材料吸收特性。为此及将水泥与石墨，羰基铁粉混合。经过混合后的水泥一般不能达到所需要的吸波性能，并且每次进行混合比例的改变都无法精确控制介质电磁参数。根据实验中的经验，最后采用分层结构进行结构吸波材料设计，结构如图1所示。

图1　基于水泥的结构吸波材料

水泥结构吸波材料的总厚度为20毫米，其中第一、三、五层为接近空气的低介电常数材料，第二、四层为有添加剂的水泥材料。采用这样设计的原理是因为水泥材料的介电常数与磁导率要大于空气的介电常数与磁导率，因此水泥材料的波阻抗无法与空气的波阻抗匹配，这样不能减少电磁波的反射。通过采用如图1所示的结构，可以降低材料的有效介电常数与磁导率，这样达到了与空气介质匹配的目的，减少了电磁波的反射。同时，在水泥中加入吸波的添加剂，可以进一步将电磁能转化为热能，提高了吸波性能。对于添加剂的水泥材料而言，以体积分数来计，其中碳纤维占1.320%，金属碎屑为0.066%，羰基铁粉3.300%，石墨占33.000%，其余均为水泥灰粉末。经过调配以后加入适量的水，从而得到该试验中所用的材料样本。

2结构吸波材料测量

双端口传输与反射测量技术既可以用于同轴线传输线，也可以用于波导结构的传输线。一般讲，同轴线结构的被测样品制作相对复杂一些，同时样品的尺寸非常小，加工起来有一定的困难。波导结构的样品制作要容易一些，但是单模工作条件会限制测量的频率范围。我们以下的分析针对波导结构，相应的波导结构测量模型如图1所示。图2中待测样品放在中间位置，波导两端为测量散射参数的参考面。

图2　波导测量电磁参数模型。中部是待测介质，两边是空气介质

2.1　参考面位置无关的公式

根据文献[11][12]，为了避免测量参考面位置对参数提取结果的影响，首先将散射参数进行预处理。通过对散射参数的组合分析，得到如公式(1)和(2)所示的A，B参数。

(1)

B=exp[2γ0·(Lair-L)]·(S21·S12-S11·S22)

(2)

其中在公式(1)和(2)中的参数由公式(3)到(6)决定。

(3)

(4)

(5)

(6)

从公式(1)和(2)中，可以看到，这两个参量与测量参考面无关，因此可以去除由于参考面位置偏差所带来的计算结果误差。通过求解方程(2)可以得到：

(7)

公式(7) 带入公式(1)，得到：

(8)

求解方程(8)，得到

(9)

从以上公式可以看到，一旦我们从测量的散射参数计算得到P，Г，就可以计算求解介电常数和磁导率。在得到与参考面无关的参数A，B以后而是定义非线性函数F为：

F(εr，μr，ω)=abs(P-T)+abs(Г-R)

(10)

在公式(10)中定义的函数Г是复介电常数与复磁导率的函数，P，Г分别由公式(7)和(9)式根据实验结果计算得到。T和R采用波导中的解析公式计算：

T=exp(-γ·d)

(11)

(12)

公式(11)中的d为被测样品的厚度。通过让函数F=0，可以得到所需的材料参数。公式(10)与Baker-jarvis公式的区别在于，不再需要关心测量参考面相位的位置误差的影响。

2.2　非线性方程迭代求解方法

在迭代方法求解非线性方程(10)中，置信区域优化计算方法是一种稳定有效的求解方法。置信区域算法中使用二次超曲面模型，通过求解最小值的搜索方法得到非线性方程的解。对于非线性方程(10)，其置信区域的二次模型具有公式(13)所示的函数形式。

(13)

其中p是搜索步长，Bk是二次导数矩阵。为了达到收敛的目的，要求

‖p‖≤rk

(14)

在公式(14)中rk是n维空间置信区域的半径，搜索步长只有在小于置信区域的半径的条件下才可以得到二次曲面的极小值。

在采用迭代方法求解非线性方程的过程中，选择初值实际上就是选择置信区域，然后在这个置信区域附近求非线性函数的极值点。不同的初始值会收敛到不同的置信区域的极值点，因此选择一个好的初始猜测值对于获取合理的电磁参数是至关重要的。

通过研究非线性方程，我们发现如果

(15)

(16)

real(μr)·real(εr)<4

(17)

也就是说，如果初始猜测值介电常数的实部与磁导率的实部的乘积在偏离真实值的介电常数的实部与磁导率的实部的乘积不超过4的范围，都可以得到有效合理的介质电磁参数。换句话讲，初始猜测值位于置信区域内。图3和图4给出了数值计算研究验证上述结论。在仿真试验中，假设被测材料的介电常数和磁导率分别为：epsr=6.2-i*0.5，mur=2.0-i*0.1 。首先，选择初始猜测值 epsr0=(3.4，0.0)，mur0=(2.0，0)。这时介质的介电常数和磁导率的实部乘积等于12.4 。因此初始猜测值的介电常数和磁导率的实部乘积应该在[8.4，16.4]范围。作为实验，猜测值介电常数和磁导率的实部乘积是 3.4*2.0=6.8。由于猜测值在置信区域以外，所以得到的结果正如图3所示，与介质的参数是不符的。从结果看到，参数的实部与介质参数不符，虚部与介质参数符合。主要原因是实部影响函数的周期性，因此非线性函数收敛到不同区域的极值点。其次，选择初始猜测值 epsr0=(4.2，0.0)，mur0=(2.0，0)。这时介质的介电常数和磁导率的实部乘积等于8.4 ，在置信区域以内，得到的结果正如图4所示，与介质的参数是符合的。在实际计算中，选择乘积等于8也得到了收敛的结果，但是再减少0.1会出现其它的极值点。因此我们提出的置信范围公式(16)给出的置信区间是有效的。

图3　采用初始猜测epsr0=(3.4，0.0)和 mur0=(2.0，0)得到的介质参数

图4　采用初始猜测epsr0=(4.2，0.0)和 mur0=(2.0，0)得到的介质参数

3测量结果与讨论

针对以上制作的结构吸波材料，我们进行了散射参数的测量研究。被测的水泥样品由具有磁导率的介质，普通水泥以及具有电损耗性质的石墨混合而成。将该水泥样品制作成如图1所示的结构吸波材料用于测试。实验中采用x波段的矩形波导结构进行传输与反射测量。被测的水泥样品厚度是20毫米。测量仪器是安捷仑公司的网络分析仪。测量的频率范围从8GHz到12.5GHz。通过测量得到的散射参数采用公式(10)进行迭代计算，迭代初值选为：epsr0=(3.0，0.02) ，mur0=(3.0，0.0) 时得到的介电常数与磁导率如图5所示。

图5　多层结构吸波材料的等效介电常数与磁导率

为了进一步验证测量的结构吸波材料的等效介电常数与等效磁导率，我们将得到的等效介电常数与等效磁导率带入波导结构的散射参数计算公式中，将计算得到的散射参数与测量得到的散射参数进行比较。计算与测量的比较结果如图6和图7所示。图6是s11散射参数实部与虚部的比较结果。图7是s21散射参数实部与虚部的比较结果。两个结果表明测量结果与提取参数计算的结果在大部分频率范围一致。在8GHz附近有一些偏差。但是从纵坐标看，透射系数的数值非常小，因此测量的相对误差要大一些。

另外从介电常数，磁导率随频率变化的曲线可以看到，该水泥样品的介电常数是一个随频率变化的函数，这种随频率的变化对于散射参数的相位变化是不敏感的。

综上所述，在本文的研究中，我们给出了一种水泥结构吸波材料的设计。采用该设计，制作了一种宽带结构吸波材料，该吸波材料的反射系数小于-10dB。用参考面无关的方法测量了结构吸波材料的等效介电常数与等效磁导率。最后对等效介电常数与等效磁导率进行了计算验证，计算结果与测量结果符合良好。

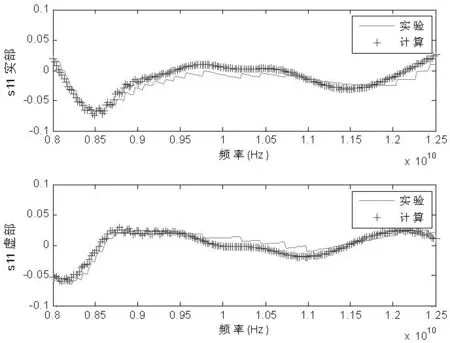
图6　多层水泥结构吸波材料的计算S11参数与测量S11参数比较

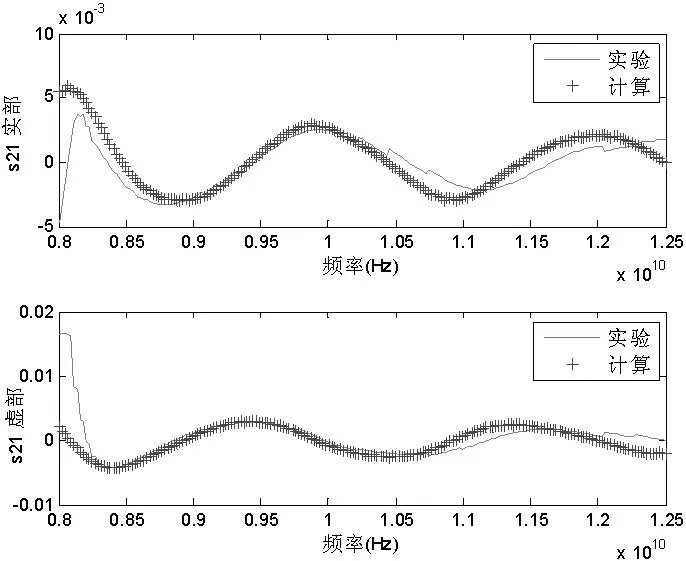
图7　多层水泥结构吸波材料的计算S21参数与测量S21参数比较

参考文献

[1]许卫东，等.铁氧体水泥基微波吸收复合材料的初步研究[J].兵器材料科学与工程，2003，26(6)：6-10.

[2]康青.手性吸波混凝土研制与展望[J].材料导报，2005，19(4)：74-76.

[3]管洪涛，等.EPS水泥复合材料的吸波性能与抗压性能研究[J].材料科学与工程学报，2006，24(4)：524-527.

[4]熊国宣，等.纳米TiO_2与水泥复合材料的吸波机理探讨[J].功能材料，2007，38(5)：836-841.

[5]熊国宣，等.水泥基复合材料的吸波性能[J].硅酸盐学报，2004，32(10)：1281-1284.

[6]M N Afsar，et al.The measurement of the properties of materials[J].proc IEEE，1986，74(1)：183-199.

[7]M A Stuchly，et al.Coaxial line reflection method for measuring dielectric properties of biological substances at radio and microwave frequencies—A review[J].IEEE Trans Instrum Meas，1980，29(9)：176-183.

[8]D K Godgaonkar，et al.Free-space measurement of complex permittivity and complex permeability of materials at microwave frequencies[J].IEEE trans Microwave Theory Tech，1990，39(4)：367-394.

[9]A Boughriet，et al.Noniteritive stable transmission/reflection method for low-loss material complex permittivity determination[J].IEEE Trans Microwave Theory & Tech，1997，45(1)：52-56.

[10]W B Weir.Automatic measurement of complex dielectric constant and permeability at microwave frequencies[J].Proc of IEEE，1974，62(1).

[11]K Chalapat，et al.Wideband Reference-Plane Invariant Method for Measuring Electromagnetic Parameters of Materials[J].IEEE Trans MTT，2009，48(9)：1-11.

[12]J Baker-jarvis，et al.Improved technique for determining complex permittivity with the transmission/reflection method[J].IEEE trans MTT，1990，38(8)：1096-1103.

[13]M.Driss Belrhiti，et al.Complex permittivity of low loss materials in X band[J].Intl Journal of Sci & tech，2011，1(6)：221-224.

[14]Ugur C.Hasqr，et al.Noniterative permittivityextraction of lossy liquid materials from reflection asymmetric amplitude-only nicrowave measurements[J].IEEE Trans，Microwave and wireless components letters，2009，19(6)：419-421.

(责任编辑：王谦)