基于混合Copula函数的金融市场非线性极端风险传染研究
淳伟德,付君实,赵如波(成都理工大学商学院,四川成都610059)
基于混合Copula函数的金融市场非线性极端风险传染研究
淳伟德,付君实,赵如波
(成都理工大学商学院,四川成都610059)
摘要:本文在金融市场典型事实约束下,运用ARFIMA和FIAPARCH模型分别对金融收益率与波动率进行建模,以排除金融市场典型事实对风险传染效应的影响,进而运用极值理论( EVT)对标准收益的极端尾部建模,并运用由Clayton、Frank和Gumbel组成的混合Copula模型对金融风险传染进行实证研究。研究结果表明:次贷危机的爆发对于股市的长记忆性具有一定的影响;在次贷危机后,中国大陆股市与香港股市、日本股市以及新加坡股市发生了显著的极端风险传染,而香港股市与日本股市、新加坡股市以及日本股市与新加坡股市之间未发生显著的极端风险传染。
关键词:极端风险传染;典型事实;极值理论;混合Copula
1 引言
随着金融全球化不断推进,全球金融市场得到了共同发展与繁荣,但是随着金融深化程度的加深以及各国金融管制的逐步放松,使得金融风险更易爆发和传染,可能导致局部性风险危机演变为全球性金融危机。而纵观近年国际金融市场,金融危机频繁爆发,其影响深度与范围正在不断地增强,比如2008年美国的次级贷款危机相对于1997年东南亚金融危机危害损失更为巨大,范围更广。此外,有研究还表明,在金融市场下滑期间市场联动性高于上升期间[1],也就是说当金融市场发生风险危机时,金融风险可能以更快的速度向其他联系密切的金融市场传染,从而加剧了风险危机的蔓延。因此,研究不同金融市场之间的风险传染效应,特别是极端风险传染效应,对于维护经济安全,促进经济繁荣,推动经济社会和谐发展,都具有极其重要的理论价值与实践意义。
自1997年亚洲金融危机以及美国次贷危机爆发以来,国内外许多学者围绕金融市场风险传染进行大量卓有成效的研究。迄今为止,已有一部分学者基于传统数理统计方法对金融风险传染进行了实证研究[2],也有学者运用Granger因果检验与VAR方法研究了金融风险传染[3]。但是需要指出的是,金融市场作为一个复杂的非线性系统,金融风险传染很可能是以非线性方式进行的,而基于传统数理统计的相关性检验、Granger因果检验以及VAR方法却只能够检验变量的线性关系,从而很难准确地测度出不同金融市场是否存在风险传染关系,因而其研究结论必然与实际情况存在有较大差距。因此,研究金融市场极端风险传染必须使用非线性模型,才能够使得实证结果更加准确可靠。
近年来,大量学者开始运用非线性Copula函数来研究不同金融市场风险传染,取得了较好的研究成果。就常用Copula函数而言,有椭圆型Copula函数、阿基米德Copula函数、非线性Copula函数等,于是选择什么样的Copula函数来研究金融风险传染就成为一个重要的问题。而事实上,测度风险传染最为关键之处在于能否准确刻画金融收益相依结构。单一Copula函数在刻画市场的相依结构方面,存在较为明显的不足之处。比如说,椭圆型Copula函数只能够刻画对称相依关系,Gumbel-Copula无法捕捉金融收益分布的下尾相依性特征,而Clayton-Copula函数虽然可以刻画下尾相依关系,但却无法刻画分布上尾的相依结构[4]。因此,本文将使用由几种Copula函数构成的混合Copula函数来测度金融市场极端风险传染。
然而,必须指出的是,自20世纪70年代以来,由于金融数据获取能力的增强以及计算机科学与技术的迅猛发展,产生了大量诸如自相关性、波动聚集性、杠杆效应等典型事实特征[5],这些典型事实对金融市场运行实质具有显著的影响,因而研究风险传染必须以典型事实为约束条件展开,ARFIMA和FIAPARCH模型恰恰能够准确地刻画诸如自相关、波动聚集性等多种典型事实特征,因而运用ARFIMA以及FIAPARCH模型能够剔除多种典型事实特征,获得反映金融市场运行实际的新生序列。同时,相对于一般风险,极端风险具有更强的传染性,能够迅速扩散,造成股市剧烈下跌甚至金融危机等严重后果,这就要求我们应该更加关注极端风险。金融收益的尾部恰恰代表着极端风险,其分布特征十分复杂,传统单一分布假设并不符合实际情况,而极值理论不必预先假设整个样本所服从的分布特征,只需对极端尾部进行建模[6],所以应用极值理论于金融风险传染测度中,能够有效克服对于极端尾部单一分布假设的缺陷,使得风险传染测度更加准确可靠。
中国大陆金融市场经过20多年的发展已成为全球最大的新兴金融市场之一,但是长期以来,由于开放程度较低等原因,与国际金融市场基本处于分割状态。近年来,随着中国大陆资本市场的不断开放,境外资本加速流入中国大陆市场,同时金融制度改革也取得了重大成就,使得中国大陆金融市场日益成熟与完善,与世界金融市场不断融合[7],这必然加深中国大陆股市与其他国际股市特别是周边国际股市的联系。在中国周边国际股市中,香港作为一个国际性金融中心城市,同时也是中国与世界进行经济联系的窗口,而日本是全球第二大股市,其在世界资本市场占据重要位置,新加坡是东盟最发达国家,同时也是亚洲最为重要的金融中心之一。因此,探讨中国大陆股市与周边国际股市之间的风险传染,特别是极端风险传染,具有明确的理论价值与实际意义。
基于以上分析和认识,本文以中国大陆与周边国际股市为研究对象,引入ARFIMA与FIAPARCH模型捕获金融收益与波动率的更多典型事实特征;针对金融收益序列极端尾部分布的复杂性特征,引入极值理论( EVT)对其进行建模,获得能够反映金融市场运行实际特征的“新生序列”,然后运用混合Copula函数分析探讨金融市场之间的极端风险传染。力求通过相关理论分析与实证研究,重点讨论并回答以下两个问题: ( 1)中国大陆股市与周边国际股市尾部相依系数在次贷危机后是否增加?
( 2)中国大陆与周边国际股市是否发生极端风险传染?
迄今为止,已有学者对金融市场风险传染进行了研究。赵华[8]运用多元GARCH模型研究了次贷危机时期41个国家(地区)的股市风险传染。李志辉和王颖[9]运用VEC模型分析了中国债券市场、外汇市场以及股票市场之间的风险传染效应。陆静等[10]运用VAR模型和Granger因果检验研究了欧债危机期间欧洲9个国家主权债券的风险传染效应。曹源芳和蔡则祥[11]运用Granger因果检验和脉冲响应函数研究了中国国内各区域风险传染效应。虽然上述学者的研究均取得了较好的研究成果,但是由于其采用的是线性模型,而金融市场风险往往以非线性方式传染,因而其研究仍然存在较为显著的不足之处。于是有学者开始采用非线性的Copula函数来研究风险传染,如龚朴和黄荣兵[12]运用时变t-Copula模型研究了次贷危机期间中美股市间的风险传染。Rodriguez[13]运用机制转换Copula模型研究了亚洲金融危机期间东亚五国间股市风险传染效应。黄在鑫和覃正[14]运用Copula函数研究了中美金融市场之间的风险传染以及传导路径。但是,上述学者在研究时并未将金融市场广泛存在的典型事实特征加以考虑,而且运用的是单一Copula函数,因而其研究结果与实际情况仍然存在差距。而本文首先通过提炼出有价值的典型事实以此确定边缘分布模型,排除了典型事实特征的影响,从而获得了金融市场运行的本质特征,进而运用混合Copula模型来研究金融市场极端风险传染。由此可见,与已有的研究文献相比,本文的差异性是显而易见的。
2 研究方法
2.1基于典型事实的边缘分布模型设定
运用Copula理论测度金融风险传染关键在于对收益率的边缘分布的设定,这是因为运用Copula建模时要求边缘分布为独立同分布,而典型事实的存在使得收益率序列并非独立同分布,只有过滤掉波动率后才能剔除冗余信息得到独立同分布序列。金融市场收益率一般具有显著的自相关性,同时还可能具有长记忆性的典型事实特征。因此,本文引入能够捕获自相关以及长记忆的ARFIMA模型对金融收益率建模,我们使用的是ARFIMA( 1,d1,1)模型,其表达式为其中rt是金融资产收益序列,u为条件均值,L为滞后算子,d1称为分整阶数,εt为残差项,Φ( L)与Θ( L)分别为自回归滞后算子以及移动平均滞后算子。
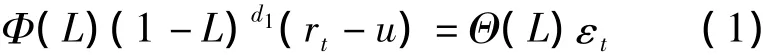
另外,大量的研究表明金融市场收益率不仅具有明显的异方差性,还可能存在杠杆效应以及长记忆性[15]。因此,本文采用FIAPARCH( 1,d2,1)模型对金融收益波动率σt进行建模,其表达式如下其中ω为常数项,γ为杠杆系数,d2为分整阶数,L为滞后算子,β( L)和φ( L)分别为自回归滞后算子以及移动平均滞后算子,δ为势项参数。
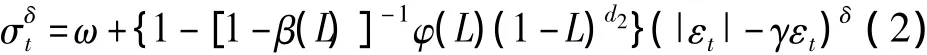
基于以上描述,本文运用ARFIMA和FIAPARCH模型分别对金融收益率和波动率建模,由于金融收益率还常常存在有偏和胖尾这两种典型事实,因此本文选用有偏学生t分布刻画标准残差序列。并采用有偏学生t分布来刻画收益分布的有偏和胖尾典型事实特征,然后运用( 3)式计算得到其标准收益率(也称条件收益率) zt,即其中rt为收益率,^ut为条件均值,^σt为条件标准差。

金融收益序列的极端尾部分布特征相对更为复杂,往往不服从某一特定分布,而极值理论( Extreme Value Theory,EVT)不必预先假设整个样本所服从的分布特征,只须对分布的极端尾部进行建模,因而能够有效克服传统风险管理的单一分布假设的缺陷,使风险传染测度更加准确。本文将采用分段方法对标准收益序列进行积分变换,即:对处于上下尾部阈值之间的标准收益序列采用经验分布函数进行积分,而对落入上下尾部的标准收益序列,则运用提高门槛模型( POT)建立累积分布函数。POT模型更加关注的是随机变量z超过某个阈值u的条件极端损失分布函数Fu,当阈值充分高时,超过阈值的收益率序列近似服从广义帕累托分布,即其中y是随机变量,u是阈值,ζ是尾部形状参数,β是标度参数。
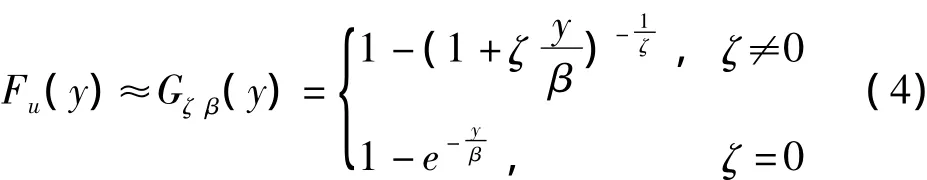
在阈值u的选择上,本文参照DuMouchel[16]选择10%的数据作为极值建模,并使用极大似然估计方法得到GPD模型的参数ζ和β。
2.2基于混合Copula的金融极端风险传染测度
模型
正如前面引言中所论述的那样,阿基米德Copula函数中的Gumbel、Clayton和Frank函数能够很好地刻画金融收益尾部相依关系。
Clayton函数的分布函数表达式为
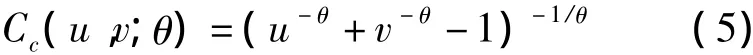
Frank函数的分布函数表达式为
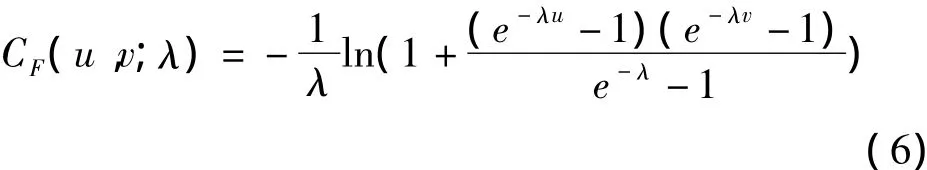
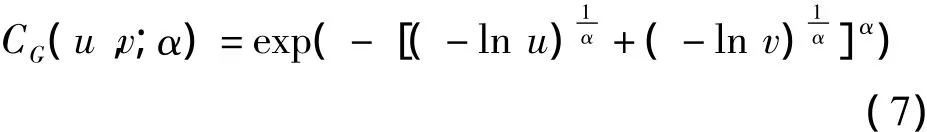
Gumbel函数的分布函数表达式为其中u,v分别为边缘分布函数,θ,λ,α分别为Copula函数相依性参数。
以上三种阿基米德Copula函数在刻画尾部相依结构方面各有优劣,例如Gumbel能够刻画上尾部相依关系,却不能刻画下尾部相依关系; Clayton虽然可以刻画下尾部相依关系,但却无法刻画上尾部相依结构。因此,如果仅仅单纯用上述某一种Copula函数很难准确描述金融市场的尾部相依关系。
为了更为全面可靠地刻画金融市场的尾部相依结构,本文考虑使用阿基米德Copula函数中Clayton、Frank和Gumbel函数进行组合所构成的混合Copula函数,对不同市场的尾部相依结构进行拟合。其中Cc表示Clayton函数,Cf表示Frank函数,Cg表示Gumbel函数,ωi( i = 1,2,3)表示三种Copula函数的权重。
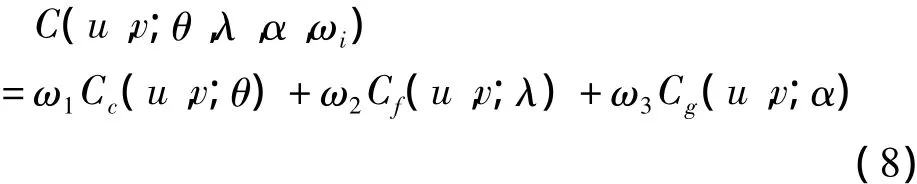
在Copula函数刻画的相依关系中,尾部相依关系表示的是金融市场在极端情况下相互影响的概率,其中下尾部相依系数表示的是一个股票市场暴跌时,另一个股市也出现暴跌的概率,下尾部相依系数可以通过如下公式求得其中λL为下尾部相依系数。

2.3金融市场风险传染测度模型的可靠性检验方法
能否准确测度金融市场相依性对于研究风险传染效应显得尤其重要,本文通过拟合优度检验方法来考察Copula模型是否能够准确地刻画变量的相依结构。
如果边缘分布变量序列{ ut}和{ vt},t =1,2,…,T,均服从i.i.d( 0,1)均匀分布,将区域[0,1]× [0,1]分为k×k个单元格,记第i行第j列单元格为Aij,i,j =1,2,…,k。
设Qij、Eij(δ^)分别为数据点落在单元格Aij中的观察点数和由混合模型计算预测数所落在Aij单元格中的频数。χ2统计量为其中E(δ^) = np(δ^),p(δ^) =c( u,v;δ^)。n为
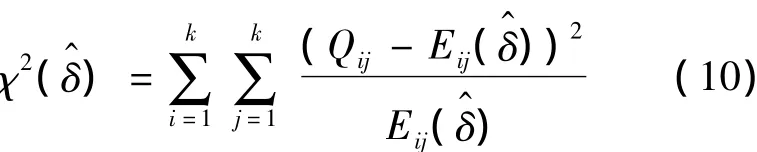
ijijijAmij变量长度,pij为数据点落在单元格Aij的概率值,c为混合Copula函数,δ^为混合Copula参数。
m
检验统计量χ2(δ^)是否服从自由度为( k-1)2的卡方分布。如果模型有m个参数,k个单元格被合并,则χ2统计量的自由度为( k-1)2-m-k +1。对于给定的显著性水平α,如果χ2(δ^)>χ2,则拒绝原假设,说明模型不能描述
( ( k-1)2-m-k +1)时间序列的相依结构关系。反之,模型则能够捕获相依结构关系。
3 实证结果与分析
3.1样本选取与说明
为了揭示中国大陆股市与周边国际股市之间的风险传染情况,本文以沪深300指数( CSI300)、恒生指数( HSI)、日经225指数( N225)、新加坡海峡指数( STI)作为研究对象。由于次贷危机于2008年4月4日正式爆发,而次贷危机对亚洲股市均产生了严重的影响,为了考察次贷危机对亚洲股市风险传导关系的影响,本文将整个样本划分为两个阶段:即从2005年1月1日至2008年4月4日为次贷危机爆发前,2008年4月5日至2012年12月31日为次贷危机爆发后。由于上述4个股市存在交易日期差异,本文将不一致的交易日期进行剔除处理。
3.2描述性统计与边缘分布模型估计
本文首先对四个收益率序列进行简单的描述性统计,从描述性统计结果中可以看出,四个股市收益率均值在次贷危机爆发前均为正值,而在爆发后变为负值;除香港股市外,其余股市偏度均为负值,这也说明除次贷危机前的香港股市外均存在有偏特征;峰度均显著大于3,即存在尖峰以及厚尾特征;而J-B值统计量表明,四个市场的收益率序列在1%的显著性水平均拒绝正态分布; Q统计量表明四个收益率序列均存在显著的自相关特征;而ARCH效应检验结果表明四个收益率序列均存在显著的ARCH效应。
从上面的描述性统计,我们可以发现这四个收益率序列存在显著的自相关以及异方差等典型事实特征,正是由于这些典型事实特征的存在可能使得收益率序列不服从独立同分布,如果使用混合Copula函数对这些收益率序列进行建模分析,则可能得到不准确的结果。因此,本文首先运用ARFIMA-FIAPARCH-skst模型来对四个收益率序列分别建模,力求消除典型事实特征对于金融市场运行实际特征的影响。
从模型的参数估计结果可以看出,在次贷危机爆发前仅中国大陆股市收益率序列存在长记忆性,而波动率除新加坡股市外均存在长记忆性,次贷危机爆发后四个股市收益率序列均不存在长记忆性,而波动率均存在着长记忆性。同时,四个股市在次贷危机前杠杆效应参数γ均不显著,而在次贷危机爆发后恒生指数以及日经225指数的杠杆效应参数γ显著,表明在次贷危机爆发前,四个股市均不存在显著的杠杆效应,而在次贷危机后香港股市以及日本股市表现出显著的杠杆效应。为了检验边缘分布模型能否剔除典型事实特征对于金融收益序列的影响,即得到的标准收益序列是否服从[0,1]均匀分布,于是本文对经过边缘分布模型处理的标准收益序列进行了K-S检验,所有K-S统计量均在1%或者5%显著性水平下显著,表明经过处理的标准收益率序列均服从i.i.d[0,1]均匀分布,能够满足Copula函数建模的需要,因而用此边缘分布模型来处理数据是合适的。
3.3基于混合Copula模型的极端风险传染检验
与分析
通过以上步骤建模,得到了四个股市已排除了典型事实影响的标准收益序列,并且这四个标准收益序列均服从[0,1]均均分布,因而我们可以进一步建立相依结构模型,分析四个股市的尾部相依结够,从而测度股市之间的极端风险传染关系。研究股市极端风险传染无论是对于构建风险防火墙,还是为投资者规避巨额投资损失提供有价值的参考信息都具有重要的意义。在使用Copula函数分析尾部相依关系之前,我们首先运用散点图和二元频率直方图对其进行初步的研究。从次贷危机爆发前后中国大陆股市与香港股市标准收益的散点图和二元频率直方图可以看到,在次贷危机爆发前两个股市的标准收益散点图分布较为零乱,散点在主对角线上分布略多于副对角线,在极端尾部的分布频率高于中心区域。而在次贷危机爆发后,标准收益的散点主要分布于主对角线,特别是在两个极端尾部区域明显高于其中心区域。其余股市之间的尾部相依结构也与中国大陆股市和香港股市相类似,散点主要集中于主对角线以及极端尾部区域。因此,四个股市之间呈现出明显的正相关关系,并且在尾部的相关性较强,即在极端情况下易相互影响。
基于以上的经验分析,我们首先使用由Clayton、Frank和Gumbel三者组成的混合Copula函数来对四个市场的尾部相依结构进行初步的分析,通过综合分析参数估计结果,我们可以知道在混合Copula函数中Clayton函数权重更大,即四个股市之间更多地体现为下尾部相依关系。对于金融市场是否发生风险传染,我们可以通过对比危机前后的尾部相依系数。在次贷危机前中国大陆股市与香港股市、日本股市以及新加坡股市的下尾相依系数分别为0.07、0.02、0.09,而次贷危机爆发后增长到了0.28、0.09、0.18,香港与日本以及新加坡股市的的下尾相依系数分别由0.29、0.33下降至0.24、0.31,日本与新加坡股市的下尾相依系数则由0.33下降至0.27。根据实证结果可知,中国大陆股市与香港股市、日本股市以及新加坡股市发生了显著的极端风险传染,而香港股市与日本股市以及新加坡股市、日本股市与新加坡股市并未发生极端风险传染。在次贷危机期间中国大陆股市受到了多个市场的风险传染,其原因可能是在次贷危机爆发前,中国大陆股市与周边股市基本处于隔离状态,随着中国资本市场的逐步开放,中国大陆股市与周边股市之间的联系较之前均有一定程度增加;当次贷危机爆发后,美国股市产生的极端风险迅速传染至香港等国际股市,而这些股市作为风险的中转站,将金融风险间接传染至中国大陆股市。对于香港、日本以及新加坡股市而言,未发生极端风险传染的原因可能是由于这些市场均为开放性的国际性金融市场,彼此之间的相关性在次贷危机爆发前均较高,次贷危机爆发后并没有增加这些股市之间的联系,因而这些股市之间未发生极端风险传染。
为了证明我们的模型取得了较好的拟合效果,下面进行严谨的统计检验,即进行χ2检验,检验时将区域[0,1]×[0,1]分成k×k个小区域进行检验,所得到的检验结果均显著,则表明混合Copula模型均通过了拟合优度检验。因此,由Clayton、Frank和Gumbel组成的混合Copula模型能够很好地拟合数据,从而能够较好地刻画股市间的尾部相依结构,因而使用混合Copula模型来测度金融市场极端风险传染是合适的。
4 结论
本文在众多典型事实约束下,运用ARFIMAFIAPARCH-skst模型对沪深300指数、恒生指数、日经225指数以及新加坡海峡指数建立了收益-波动模型,得到了排除典型事实影响的标准收益,在此基础上运用由Clayton、Frank和Gumbel组成的混合Copula函数对金融市场尾部相依结构进行建模,从而分析股市之间的风险传染效应,取得了较好的研究效果。研究结果表明:
( 1)在次贷危机爆发前,沪深300指数的收益率和波动率呈现出显著的长记忆性,恒生指数和日经225指数的波动率呈现长记忆性,新加坡股市不存在长记忆性,这可能预示着在次贷危机爆发前中国大陆股市对于信息的反应比较迟缓,需要一段较长的时间来消化过去的信息,而新加坡股市对于信息的反应则最为迅速,而在次贷危机爆发后,四个股市仅波动率呈现出显著的长记忆性,表明在次贷危机爆发后四个股市对于信息的反应均较为及时。
( 2)排除典型事实可能存在的影响之后我们可以看到,在次贷危机后中国大陆股市、香港股市、日本股市以及新加坡股市彼此间存在着较强的尾部相依关系,特别是下尾部相依关系,由此说明上述四个股市之间在市场下跌期间的关联性强于市场上升时期,因此无论是投资者还是风险管理部门对于周边股市的尾部风险应该引起足够的重视,尤其是对一些极端事件引发的股市动荡更应该积极防范,避免其带来不必要的损失。
( 3)中国大陆股市与香港股市、日本股市以及新加坡股市发生了显著的极端风险传染,而香港股市与日本股市以及新加坡股市、日本股市与新加坡股市之间没有发生显著的极端风险传染,由此说明随着中国大陆金融市场不断开放,中国大陆股市与周边国际股市之间的联系更加紧密,特别是风险危机事件的爆发更是进一步增加了中国大陆股市与周边国际股市之间的联系。
参考文献:
[1]Patton A J.Modelling asymmetric exchange rate dependence[J].International Economic Review,2006,47 ( 2) : 527-556.
[2]Forbes K J,Rigobon R.No contagion,only interdependence: measuring stock market comovements[J].Journal of Finance,2002,57( 5) : 2223-2261.
[3]Hong Y,Liu Y,Wang S.Granger causality in risk and detection of extreme risk spillover between financial markets [J].Journal of Econometrics,2009,150(2) : 271-287.
[4]Hu L.Dependence patterns across financial markets: a mixed copula approach[J].Applied Financial Economics,2006,16( 10) : 717-729.
[5]Cheng W H,Hung J C.Skewness and leptokurtosis in GARCH-typed VaR estimation of petroleum and metal asset returns[J].Journal of Empirical Finance,2011,18( 1) : 160-173.
[6]Fernandez V.Risk management under extreme events [J].International Review of Financial Analysis,2005,14( 2) : 113-148.
[7]王永巧,刘诗文.基于时变Copula的金融开放与风险传染[J].系统工程理论与实践,2011,31(4) :778-784.
[8]赵华.国际股市区域风险传染研究[J].厦门大学学报(哲学社会科学版),2009,( 5) :106-113.
[9]李志辉,王颖.中国金融市场间风险传染效应分析——基于VEC模型分析的视角[J].现代财经(天津财经大学学报),2012,( 7) :20-27.
[10]陆静,胡晓红,阮小飞.欧债危机的传导路径和传染效应研究[J].统计与决策,2013,( 17) :147-151.
[11]曹源芳,蔡则祥.基于VAR模型的区域金融风险传染效应与实证分析——以金融危机前后数据为例[J].经济问题,2013,( 10) :59-64.
[12]龚朴,黄荣兵.次贷危机对中国股市影响的实证分析——基于中美股市的联动性分析[J].管理评论,2009,21( 2) :21-32.
[13]Rodriguez J C.Measuring financial contagion: a copula approach[J].Journal of Empirical Finance,2007,14 ( 3) : 401-423.
[14]黄在鑫,覃正.中美主要金融市场相关结构及风险传导路径研究——基于Copula理论与方法[J].国际金融研究,2012,( 5) :74-82.
[15]Dowd K.Measuring market risk[M].Hoboken: John Wiley&Sons,2007.
[16]DuMouchel W H.Estimating the stable index α in order to measure tail thickness: a critique[J].The Annals of Statistics,1983,11( 4) : 1019-1031.
The Study on the Financial Market Nonlinear Risk Contagion Based on Mixed Copula Model
CHUN Wei-de,FU Jun-shi,ZHAO Ru-bo
( Commercial College,Chengdu University of Technology,Chengdu 610059,China)
Abstract:The paper uses the ARFIMA and FIAPARCH model to model return and volatility based on some stylized facts respectively,which can eliminate the effect on the financial risk contagion caused by stylized facts,and uses extreme value theory to measure the extreme tail.At last,the financial risk contagion is researched by the mixed copula model,which is composed of Clayton,Frank and Gumbel.The empirical results show that the outbreak of the subprime crisis has a certain impact on the long memory of stock markets,the extreme risk contagion between Chinese mainland stock market,Hong Kong stock market,Japanese stock market,and Singapore stock market is obvious after the subprime crisis.However,there is no obvious extreme risk contagion existing between Hong Kong stock market,Singapore stock market and Japanese stock market,nor does between Japanese stock market and Singapore stock market.
Key words:extreme risk contagion; stylized facts; extreme value theory; mixed copula
基金项目:国家社会科学基金资助项目( 12BGL024) ;国家自然科学基金资助项目( 71171025) ;四川省科技计划资助项目( 2012ZR0045,2013ZR0067) ;成都理工大学优秀科研创新团队资助项目( KYTD201303)
收稿日期:2014-09-05
doi:10.11847/fj.34.4.53
文章编号:1003-5192( 2015) 04-0053-06
文献标识码:A
中图分类号:F830.9

