某特种车驾驶室骨架结构的静动态分析

郭贵平，李守成，张洪生

（南京理工大学 机械工程学院，江苏 南京 210094）

0 引言

车辆工作条件多样，各零部件承载工况复杂，各种载荷作用下对结构的性能要求也不相同［1］。驾驶室骨架结构作为驾驶室的主要承载结构，应有足够的强度和刚度，同时，还要有合理的动态性能，模态频率要分布合理，以避免共振，在路面随机载荷的激励作用下，还应有良好的振动特性。因此，对驾驶室骨架结构进行静、动态分析是很有必要的。

1 驾驶室骨架结构有限元模型的建立

建立有限元模型是驾驶室结构分析的第一步，本文使用HYPERMESH软件下的ANSYS模块来建立适合于ANSYS计算的有限元分析模型。首先在Pro/E中建立某特种车驾驶室骨架结构的三维模型，如图1所示；然后用Pro/E将已经建好的骨架模型导出IGES格式文件，在HYPERMESH中导入该IGES格式文件，对该模型进行中面抽取，由于该骨架结构多由方管和角钢组成，形状规则，对已经抽取的中面只需进行少量的几何清理和修复；其次进行网格划分，由于组成驾驶室骨架的方管和角钢厚度在1mm～2.5mm之间，属于薄壁结构，因此，采用二维壳单元进行仿真，网格划分时采用SHELL181单元，单元边长为10mm；网格划分结束后，关键的一点是要对划分好的各部分进行装配，否则，各部分网格相当于独立体，之间不会进行力和位移的传递，对于该驾驶室骨架模型，主要考虑各部分焊点的模拟，在本文中采用1D－rigid－cerig命令（节点耦合）来定义焊点单元，实践证明，该方法在车身的焊点模拟中可以满足精度要求［2］；最后，在HYPERMESH中定义材料属性和单元实常数，并赋予相应的组，本文中所用材料为宝钢B550L，弹性模量为2.07×105N/mm2，泊松比为0.3，密度为7.83×10－3g/mm3，强度极限为550MPa～650MPa，屈服极限为400MPa。

2 驾驶室骨架静态刚度与强度分析

车身静刚度目标主要有弯曲刚度和扭转刚度，结合该特种车驾驶室具体结构，本文主要分析其驾驶室骨架结构的扭转工况，这主要是由于该驾驶室长度较小而宽度较大，主要承受的是扭转载荷，该工况模拟的是一端车轮悬空或抬高的情形。

2.1 约束施加

约束施加不能出现约束不足或者是约束过多，约束不足将导致驾驶室发生刚体位移，约束过多则又会产生不切实际的附加力。本文中，右后悬置点约束前后、上下、左右3个平动自由度，左后悬置点约束前后、上下2个平动自由度，右前悬置点约束前后、左右2个平动自由度，左前悬置点释放所有自由度。

2.2 载荷施加［3］

最大扭转载荷力矩M＝0.5×前轴最大负荷G×轮距L。本文中前轴最大负荷G＝800kg，轮距L＝1.527m，取重力加速度g＝9.8N/kg，通过计算可得最大扭转载荷力矩M＝5 985.84Nm。在悬置点处施加载荷力F＝M/L＝5 985.84/1.527＝3 920N，即悬置点处施加大小为3 920N，方向相反的力，即左前悬置点施加向下的力，右前悬置点施加向上的力。

2.3 计算结果分析

图2为扭转工况下驾驶室的变形云图。驾驶室左前部分x方向上最大变形量为161.082mm，可以看到，驾驶室在扭转载荷的作用下扭转刚度偏小，应该采取适当措施加强。

图3为扭转工况下驾驶室的应力分布云图。应力最大值出现在扭转载荷施加处，其值超过488.903 MPa，超过材料屈服极限，而实际的结构中由于有特殊处理，该处不会产生如此大的应力，其余应力集中区域主要出现在复杂梁、前围横梁和后围立梁等几处，应力值范围在122MPa～183MPa之间，满足材料的屈服强度要求。

3 驾驶室骨架结构模态分析

模态分析用于确定结构的固有频率和振型，是进行谱分析必须的前期过程。本文用Lancaos法提取模态频率，模态分析前7阶固有频率和振型见表1。

从模态分析结果可以看出，结构的局部振动主要出现在顶棚梁、前围横梁及车头横梁，表明这几处刚度稍弱，应采取一定的加强措施。

图1 驾驶室骨架三维模型

图2 扭转工况下驾驶室变形云图

图3 扭转工况下驾驶室应力分布云图

表1 模态计算分析结果

4 驾驶室骨架随机振动分析

道路表面的凹凸不平对车辆产生随机激励，如果该激励过大，必将导致乘员不适，同时也将使结构产生疲劳破坏，因此进行随机振动分析是必要的。

4.1 随机载荷的处理［4］

本文分析车辆以60km/h的速度在B级路面上行驶工况的随机响应。根据国家标准GB7031－86得到空间频率位移功率谱密度值，见表2。计算时，取空间频率位移功率谱密度的几何平均值。

表2 空间频率位移功率谱密度值

在输入路面不平度位移功率谱密度值时，近似地在驾驶室骨架4个悬置点处输入相同的位移功率谱密度值。根据经验值，路面谱经过悬架过滤到悬置点后按原谱值的30%来计算。对汽车振动系统的输入除了路面不平度外，还要考虑车速这个因素。根据车速u（m/s）将空间频率位移功率谱密度Gq（n）（mm2/m－1）换算为时间频率功率谱密度Gq（f）（mm2/Hz）。时间频率f（s－1）与空间频率n（m－1）的关系为f＝un，时间频率位移功率谱密度Gq（f）与空间频率位移功率谱密度Gq（n）的换算式为Gq（f）＝Gq（n）/u，从而可以计算得到时间频率功率谱密度值［5］。最后计算出来的时间频率f及时间频率位移功率谱密度值Gq（f）见表3。

表3 时间频率和时间频率位移功率谱密度值

4.2 计算结果及分析

图4和图5为随机振动时载荷步3的变形云图和应力分布云图，图6为最大位移节点位移响应谱。这里的1σ响应值就是概率统计中正态分布下的均方根响应值，小于该均方根值的出现概率为68.27%，载荷步3能够显示1σ位移解、应力和应变值。

由图4可知，最大位移主要出现在顶棚梁处，这表明在振动68.27%的时间以内，驾驶室骨架的垂直振动位移小于7.54mm。

图4 随机振动下的驾驶室变形云图

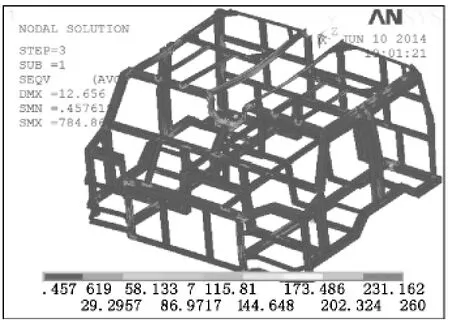
图5 随机振动下的驾驶室应力分布云图

图6 最大位移节点位移响应谱

由图5可知，该特种车以60km/h的速度行驶在B级路面时，驾驶室骨架结构整体承受的应力较小，满足材料的屈服极限要求，在路面随机激励作用下，应力集中主要出现在复杂梁和顶棚梁处，大小为58.137 MPa～86.971MPa，这表明在振动的68.27%的时间内，结构的应力值远远小于材料的屈服极限。

由图6可以看出，在频率24Hz和28Hz左右，垂向位移振动最大，该频率是驾驶室结构的第6和第11阶频率，在驾驶室设计时，应避免其他部件的固有频率与驾驶室的这两个频率重合，以免引起共振。

5 结论

通过对该特种车驾驶室骨架结构的静、动态分析，得到了结构在各种载荷工况下的变形和应力状态。静力分析表明，结构的强度符合要求，但刚度偏小，应该予以加强；模态分析结果表明，结构在顶棚梁和前围横梁及车头横梁这几处刚度稍弱，应采取一定的加强措施；随机振动分析表明，在路面激励下，驾驶室结构在24Hz和28Hz左右易发生共振，应避免其他部件的固有频率与这两个频率重合。

［1］谭继棉.汽车有限元法［M］.北京：人民交通出版社，2012.

［2］许峰.某特种车车身设计与优化研究［D］.南京：南京理工大学，2012：5－10.

［3］张雷.轿车车身刚度及模态分析研究［D］.合肥：合肥工业大学，2007：20－25.

［4］曹群豪.军用客车车身骨架结构随机振动分析与疲劳强度分析［D］.上海：上海交通大学，2007：18－29.

［5］余志生.汽车理论［M］.北京：机械工业出版社，2009.