管件式塑料检查井的非线性分析及精度控制❋

宋 佳，曾 冬，高建和

（1.扬州大学 机械工程学院，江苏 扬州 225127；2.扬州大学 化学化工学院，江苏 扬州 225127）

0 引言

目前，管件式塑料检查井采用线性低密度聚乙烯（LLDPE）滚塑成型技术，国内滚塑工艺原材料大多为LLDPE，由材料拉伸与弯曲试验可知，LLDPE线弹性阶段短、弹性模量小、塑性好，且其断裂伸长率大。由于大型构件在深埋过程中易产生大变形，因此将其变形量作为分析与优化的主要参考量。

材料非线性与几何非线性是埋地塑料检查井有限元分析中的关键点，基于非线性力学理论和计算固体力学而发展的ABAQUS有限元软件是数值仿真的重要工具之一。本文利用Pro/E对检查井进行建模，然后导入ABAQUS进行了静态有限元分析和优化。

1 双重非线性介绍

材料非线性是由于材料本身非线性的应力－应变关系而导致结构响应的非线性。ABAQUS有限元软件分析时用一系列数据点连接成的折线图来逼近材料的应力－应变曲线，因此数据点的选取越多越接近材料的真实性质。有限元分析时应分别对LLDPE的弹性与塑性部分进行定义。

LLDPE的弹性模量E＝819MPa，泊松比γ＝0.39，ABAQUS有限元分析时还应录入真实屈服应力与真实塑性应变，录入的第一组数据为材料的初始屈服应力，塑性应变值为零。由于分析采用弯曲数据，实验所得的名义应力与名义应变非常接近真实应力应变值，其中真实塑性应变εpl与真实应变εt和真实弹性应变εel的关系为：εpl＝εt－εel。LLDPE整体弯曲应力－应变曲线如图1所示。

几何非线性是由于结构经受大挠度、突然翻转、初应力或载荷刚性化导致几何形状变化而引起结构响应的非线性。管件式检查井深埋情况下，结构受力产生大变形，因此分析中必须设置几何非线性。

图1 LLDPE整体弯曲应力－应变曲线

非线性分析的求解与线性问题只求解一组方程不同，ABAQUS/Standard采用在一个增量步内进行多次的迭代（iteration），得到合理的解后再求解下一个增量步，所有增量响应的综合就是非线性分析的近似解，即增量载荷法。

2 LLDPE检查井有限元分析

LLDPE三通检查井埋深6m，井上端接缠绕管，其质量为86.5kg/m，井周接钢带管，其环刚度S为8kN/m2。

2.1 检查井网格划分

网格划分的质量直接影响到计算的精度和速度。管件式埋地三通检查井模型中有部分中空结构，且整体模型形状复杂，无法对其进行结构简化，质量较高的六面体网格无法使用，因此对其划分了较密的修正二次四面体单元，如图2所示。

2.2 载荷与约束的施加

2.2.1 载荷施加

基于散固耦合理论与土力学理论，参照《塑料排水检查井应用技术规程》可知，检查井深埋工况下主要受侧向土压力、竖向土压力、下曳力、缠绕管的重力以及缠绕管所受下曳力。在ABAQUS中根据实际埋深工况对模型进行如下加载。

图2 检查井网格划分

（1）竖向土压力标准值Fsv，k（kN/m2）：

其中：γs为回填土重度，取γs＝18kN/m3；Hs为检查井收口处覆土厚度，m。

（2）侧向土压力：

地下水位以上部分：

地下水位以下部分：

其中：Fep，k为地下水位以上的侧向主动土压力标准值，kN/m2；Ka为主动土压力系数，取Ka＝1/3；Z为地面至计算截面处的深度，m；F′ep，k为地下水位以下的侧向主动土压力标准值，kN/m2；Zw为地面至地下水位的距离，m；γ′s为地下水位以下回填土的有效重度，kN/m3。

（3）检查井壁单位面积上的平均下曳力标准值TA（kPa）：

其中：μ为检查井壁与回填土间的摩擦因数，取μ＝0.2；Fep，K1为检查井顶部侧压力标准值，kPa；Fep，K2为检查井底部侧压力标准值，kPa。

2.2.2 约束的处理

有限元计算中必须对约束条件的处理给予足够的重视，如处理不当，就不可能获得符合实际的结果，甚至方程会出现奇异。约束处理如下：

（1）在井口正上方建立参考点，将缠绕管的重力与其所受的下曳力加载于参考点上，并对参考点与检查井承受缠绕管重力部分设置Distributing Coupling。

（2）检查井底端按照管基支撑角范围内区域进行弹性固定。

（3）钢带管环刚度S＝EI/D3（D为管平均直径），由于管弹性模量E和管壁单位长度截面惯性矩I难以测量，所以环刚度是由试验测得，因此无法对钢带管进行建模分析，故将钢带管的支承作用换算成变形量施加于钢带管与井侧接触部位。钢带管在外压作用下其竖向变形量Δr为44.94mm。

（4）3个钢带管接口端面均为对称约束。

2.3 检查井分析结果

在埋深6m工况下考虑几何非线性及材料弹－塑性，利用ABAQUS进行静态有限元分析，结果如图3～图6所示。由图3～图6可知：最大应力为28.15 MPa，位于两条长筋与井口交接处，低于材料的弯曲强度；3方向综合最大变形为94.7mm，位于上井口处，这是由于竖向土压力、缠绕管重力及其下曳力共同作用所致。

图3 检查井整体应力云图

图4 检查井X方向位移云图

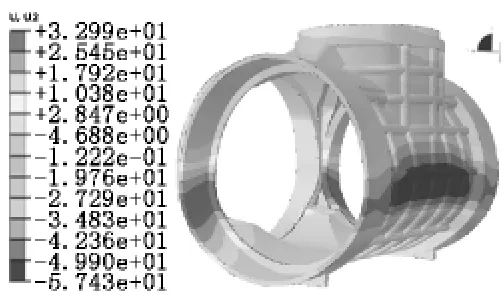
图5 检查井Y方向位移云图

图6 检查井Z方向位移云图

2.4 精度控制

有限元分析结果中的数值精度取决于所用的网格，当几何形状复杂时完全采用六面体单元构造网格会很困难，因此可在必要时采用楔形和四面体（Tet）单元。线性Tet单元精度较差，而二次Tet单元（C3D10）适合ABAQUS/Standard中的小位移无接触问题，而文中的分析涉及到几何非线性，因此在进行弹塑性分析中应该使用修正的二次四面体单元（C3D10M），并且应进行网格细化研究以确保该网格对问题提供唯一的解答。ABAQUS中通过调控全局种子来改变网格大小，本文通过不断调整全局单元尺寸来细化网格，分析结果如表1所示。

由表1可见，当种子较稀疏即单元尺寸较大时，有限元分析的结果往往偏小，与实际不符。随着种子逐渐加密，最大应力与各方向位移均有所增加，当单元尺寸至20和19时分析结果非常接近，且在应力集中区域相邻单元的应力差值不超过50%，无应力不连续现象，因此可以将单元尺寸为19的结果作为该案列的最终解。

表1 不同单元尺寸分析结果

3 结论

实验得到的LLDPE各项力学参数与应力－应变曲线，为检查井的弹塑性分析提供了依据。基于土力学理论与散固耦合理论，对深埋检查井静力分析中载荷的施加与边界约束的设定做了详细的研究，对有限元分析的数值结果精度进行了探讨，通过多次调整全局单元尺寸细化网格，确保了计算的精度。

［1］刘展.ABAQUS 6.6基础教程与实例详解［M］.北京：水利水电出版社，2008.

［2］张建华，丁磊.ABAQUS基础入门与案例精通［M］.北京：电子工业出版社，2012.

［3］石亦平，周玉蓉.ABAQUS有限元分析实例详解［M］.北京：机械工业出版社，2006.

［4］王慎平，刘北英.ABAQUS中的非线性模拟［J］.机械制造与自动化，2006，35（2）：20-22.

［5］郭继武.地基基础设计简明手册［M］.北京：机械工业出版社，2008.

［6］周汉荣.土力学地基与基础［M］.北京：中国建筑工业出版社，1997.