小波新阈值法在振动信号去噪中的应用研究❋

吴存洁，谷玉海，2，徐小力

（1.北京信息科技大学 现代测控教育部重点实验室，北京 100192；2.机械科学研究总院，北京 100044）

0 引言

风力发电机组在复杂工作环境下运行，齿轮箱是风力发电机组传动系统的核心部件，风机安装环境恶劣且齿轮传动存在接触、交变啮合应力和润滑等特点，所以齿轮箱是风力发电机组中故障率较高的部件。齿轮箱的故障通常可通过振动信号分析来诊断确定［1］，由于风力发电机组中的时变和突发性噪声严重干扰对齿轮箱故障的识别，因此消除振动信号中的噪声干扰、精确提取故障信息是风力发电机齿轮箱故障诊断的关键［2］。

1 齿轮箱振动信号小波阈值去噪原理和步骤［3］

设齿轮箱信号f（m）被噪声e（m）污染，则含噪声的齿轮箱振动信号模型可以表示为：

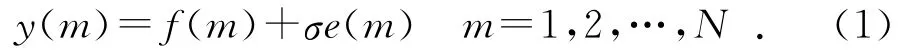
其中：y（m）为含噪声信号；f（m）为原始信号；e（m）为高斯白噪声信号；σ为信号的标准方差；N为信号的长度。

去噪就是将信号y（m）中的噪声e（m）对原始信号f（m）的影响减小到最小程度。

对含噪声的齿轮箱振动信号y（m）作离散小波变换之后分解得到小波系数dj，k。根据小波变换的线性性质，得到：

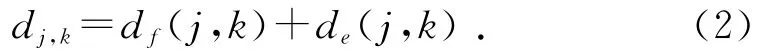
其中：df（j，k）为信号f（m）通过小波分解后得到的第j层第k个系数；de（j，k）为噪声e（m）通过小波分解后确定的第j层第k个系数。

小波阈值去噪的基本方法是：将信号通过小波基函数分解后得到的各层系数的模的大小同某阈值λ（λ＝σ）相比较，丢弃由噪声造成的低于阈值λ的系数，保留大于阈值λ的系数，然后对经过处理的小波系数再反变换，最后将有用的小波系数进行重构，得到经去噪后的真实信号。应用小波阈值去噪算法对信号进行去噪处理的主要流程如图1所示。在图1的几个步骤当中，阈值选取以及阈值量化是最重要的，决定信号去噪的质量。

图1 小波降噪流程图

2 一种新的阈值函数

2.1 传统阈值函数

目前，比较常用的阈值函数是由Donoho提出的硬阈值函数和软阈值函数。硬阈值函数为：

其中：为小波分解的j层的第k个系数对应的估计高频小波系数；ωj，k为小波分解的j层的第k个系数。

软阈值函数为：

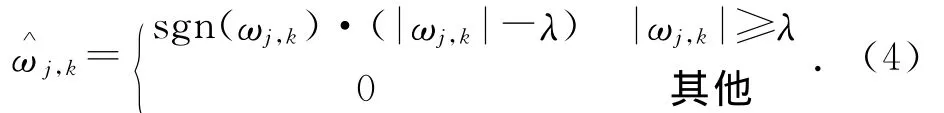
通常，硬阈值函数方法没有改变小波系数的幅值，能够很好地保留信号边缘等局部特征，但由于硬阈值函数在阈值处不连续，导致估计信号产生更大的方差，重构信号较粗糙并降低信号的光滑性；软阈值处理相对要平稳光滑，但易造成信号边缘模糊不清等非线性失真现象［4－5］。

2.2 新阈值函数算法

为了弥补软、硬阈值函数各自的缺陷，本文设计了一种新的阈值函数算法。其算法方法为：

其中：α、β、n为参数，且α∈（0，1），β∈（0，1］，n＞1/［（1－α）β］，可根据实际情况调节参数α、β、n的值。

从式（5）可以看出，新阈值函数在阈值处连续，即新阈值函数是以＝ωj，k渐近的，随着｜ωj，k｜的不断增大，不断地逼近ωj，k，解决了和ωj，k之间具有固定偏差这一缺陷，而当阈值很小时，新阈值函数同硬阈值函数相似，但更加灵活；当｜ωj，k｜≥λ时，新阈值函数是高阶连续可导的；log2可动态调整阈值，当｜ωj，k｜≥λ时，log2的值的范围是（0，1］，随着｜ωj，k｜的不断增大，或α趋近于0时，log2的值逐渐减小，这样动态地减小了软阈值方法中模值较大的小波系数的收缩，从而避免了高频信息的丢失，提高了重构信号的信噪比。

由此可见，新的阈值函数可兼顾软、硬阈值函数方法的优点。参数β用来调节阈值化小波系数与原始小波系数之间的偏差。由于经阈值λ处理后小波系数值变为（1－α）β，α和β的取值共同决定了函数由软变硬的快慢程度。α值越小，β值越大，函数越快接近硬阈值函数。

3 风机齿轮箱振动信号去噪实验

对某风场1.5MW某型号的风力发电机齿轮箱进行振动信号的采集，风速为3m/s，主轴转速为15r/min。实验使用丹麦B＆K的Type 3050-B-060采集卡，传感器使用北京测振仪器厂的CD-21有线振动速度传感器，采样频率为25.6kHz。对采集的部分频率的信号分别进行新、旧阈值函数的小波去噪，其效果如图2所示，新、旧阈值函数去噪性能分析见表1。

从图2和表1中的数据对比结果发现，新的阈值函数取得了良好的去噪效果，经新阈值函数处理后的信号其信噪比高且均方根误差低，信号谱线比传统的软、硬阈值函数更加平稳光滑，边缘明晰，贴近真实信号。可据此提炼信号的特征，再做进一步的分析即可对齿轮箱是否存在故障作出判断。

图2齿轮箱振动信号的新、旧阈值函数去噪效果对比

表1 新、旧阈值函数去噪性能分析

4 结论

通过仿真实验可以看出，本文针对传统软、硬阈值去噪的缺陷设计的新阈值函数无穷连续可导，在小波去噪的应用中取得了良好的去噪效果，并且保留了原始信号的细节特征，可以有效提取淹没在高频噪声中的微弱故障冲击信号，提高了信号的信噪比。

［1］张金敏，翟玉千，王思明.小波分解和最小二乘支持向量机的风机齿轮箱故障诊断［J］.传感器与微系统，2011，30（1）：41-43.

［2］任学平，王培.基于小波包变换的齿轮箱降噪方法研究［J］.机械制造与研究，2010，39（4）：26-28.

［3］David L Donoho.De-noising by soft-thresholding［J］.IEEE Trans on Information Theory，1995，41（3）：613-626.

［4］张晓楠，曾庆山，万红.基于改进小波去噪和EMD方法的轴承故障诊断［J］.测控技术，2014，33（1）：23-26.

［5］张德丰.MATLAB小波分析［M］.北京：机械工业出版社，2012.