反应流体的移动网格动理学格式
甄亚欣, 倪国喜(.北京应用物理与计算数学研究所,计算物理实验室,北京 00088;2.华北电力大学,数理系,北京 02206)
反应流体的移动网格动理学格式
甄亚欣1,2, 倪国喜1
(1.北京应用物理与计算数学研究所,计算物理实验室,北京 100088;2.华北电力大学,数理系,北京 102206)
在移动网格上构造一种反应流的动理学格式.首先利用BGK模型推导含化学反应的流体力学方程组,并利用其积分形式构造移动网格上离散格式,再利用自适应移动网格方法得到网格速度,最后利用时间精确的动理学数值方法构造数值通量,得到移动网格单元上新的物理量.一维与二维的数值实验表明这种格式同时具有高精度、高分辨率的特点.
反应流体力学方程;动理学格式;自适应移动网格方法
0 引言
含化学反应的流体动力学研究是爆轰流体力学的最重要部分,爆轰流体力学是伴随化学反应的强冲击波的传播过程,人们对其理论研究与相关的数值模拟的研究有较长的历史[1].早在1899年,Chapman及Jouguet等对爆轰现象作了简单的一维理论描述,形成所谓C-J理论[2-3],该理论是借助气体动力学原理而阐释的.之后,Zel'dovich、Neumann与Döring各自独立对C-J理论的假设和论证作了改进,提出所谓的ZND理论[4-6],它比C-J理论更接近实际情况,上述两种理论被称为爆轰波的经典理论,它们都是一维理论.二十世纪50年代,通过实验的详细观察,发现爆轰波波阵面包含复杂的三维结构,这种结构被解释为入射波,反射波和马赫波构成的三波结构.到二十世纪50-60年代,人们进行了大量的试验研究,实验结果显示:反应区末端状态参数落在弱解附近,而不是C-J参数,说明实际爆轰比C-J理论和ZND模型更为复杂.之后,Kirwood和Wood[7]推广了一维定常反应理论,指出定常爆轰具有弱解的可能性将随着流体的复杂性增加而增加.弱解模型为实验数据与一维理论的偏离作出了一种理论解释.从二十世纪60年代开始, Erpenbeck[8]提出了爆轰的线性稳定性理论,对一维爆轰定常解的稳定性进行了分析.后来又有人提出“方波”稳定性理论.由于实验测量技术和数值模拟工具的限制,以及固有的复杂性,研究工作有一些进展,但还存在许多困难和问题.
随着计算方法与计算技术的发展,爆轰流体力学数值模拟方法取得了很大的进步[9],目前最常用的有欧拉方法与拉氏方法.欧拉方法对应流体力学方程的Euler形式,网格固定不动,除了考虑由源项引起的变化,还必须考虑通过网格的物理量输运.然而欧拉方法在模拟多介质流动时会遇到许多问题,多介质流动问题模拟的关键之一是要确定物质界面和自由面,对于多介质界面追踪已经发展了一些有效的方法,如Hirt和Nichols[10]提出的体积份额法,Glimm[11]等提出的波阵面追踪法.这些方法在保持守恒性与克服震荡等方面还存在一些问题.拉氏方法对应流体力学方程的拉格朗日形式,由于不含输运项,拉氏方法计算公式简单,网格随流体运动,数值耗散小,界面清晰.拉氏方法可以分为两种形式,一种是交错网格型,另一种是以Godunov方法为基础的单元中心型.与交错网格方法不同,单元中心型的所有物理量定义在网格中心,它的优点是可以给出较为精确的压力与边界条件,可以保持能量守恒,该方法的不足之处是网格节点的拉氏速度由某种插值或者优化的形式获得,从而导致该方法的非物理变形.为抑制网格的扭曲变形,可以在拉氏计算中加入网格重分以提高算法的抗变形能力,Hirt和Nichols[12]所开创的ALE方法就是基于这一思想发展起来的,利用ALE方法模拟多介质流动日益受到重视,但守恒性、相容性等问题还没能很好的解决.
移动网格方法是与ALE方法比较接近的一种数值方法,Azarenok和Tang[13]发展了基于守恒插值的移动网格方法,它部分克服了ALE方法所遇到的困难,另一种移动网格方法由Harten等[14]开创,它在时空多面体上运用有限体积方法,避免了显式的重映,后被发展到高维空间,并用于化学反应流的数值模拟,但离散格式复杂,在高维时很难把握数值精度.结合动理学方法,Ni等[15]进一步发展了移动网格方法.动理学数值方法是目前流体力学数值模拟中的一种重要的方法,它从微观层次获取宏观的数值通量,与通常的数值方法相比较,有更多的物理内涵,因而可以提供更多的信息,其时间积分是精确的.动理学数值方法的基本思想是利用流体的微观描述与宏观描述的等价性,宏观Euler方程与Navier-Stokes方程可以利用Boltzmann方程得到[16].利用其简化模型,Deshpande和Mandal等[17-18]发展了一种动理学数值方法,他们将Courant-Isaacson-Reeves迎风算法用于无碰撞的Boltzmann方程,得到动力学通量向量分裂法(即KFVS方法).之后基于Bhatnagar-Gross-Krook(BGK)模型的动理学数值方法也迅速发展起来[19-21].Xu和Lian在这一方面发展了一套比较系统的方法,并用于多介质与稀薄流等问题的数值模拟[22-24].基于动理学移动网格方法是一种无重映移动网格方法,它避开了传统的移动网格方法中物理量重映带来的误差.
本文从动理学BGK模型出发,利用经典的Chapman-Enskog展开,导出含化学反应的流体力学方程,在动理学数值方法的基础上,结合移动网格技术构造了含化学反应的流体力学动理学格式.
1 移动网格反应流体力学的动理学数值方法
本节从修正的BGK模型出发,利用Chapman-Enskog展开,推导反应流体力学方程组,利用其积分形式,给出在运动标架下的离散形式,再结合移动网格方法,确定网格移动速度,实现物理量的更新.
1.1 反应流体力学方程组的BGK模型
以修正的二维的BGK模型为例,推导反应流体力学方程组,二维BGK方程为
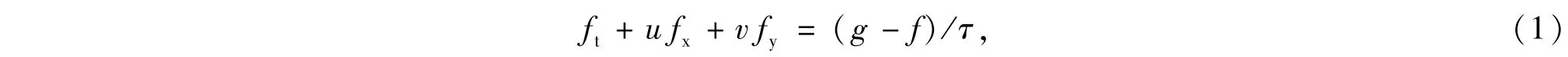
其中f是微观粒子的分布函数,g是逼近f的平衡态分布函数,(u,v)是微观粒子的运动速度,在包含多组分时,f与g可表示为
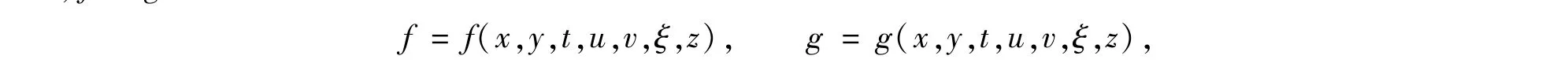
其中z为组分参量,在描述单介质的流体时,f与g一般表示为

它们与z无关,这里增加一个自由度后,就可以从BGK模型方程得到扩展的含化学反应的流体力学方程.相应地,多组分的平衡态分布有
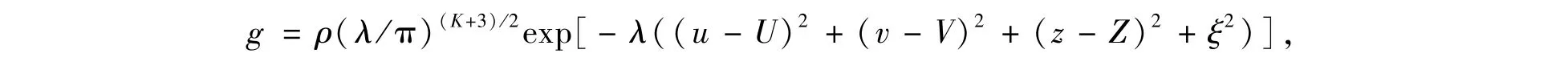
这里λ=m/(2kT),m是微观粒子的质量,k是Boltzamn常数,T是宏观温度,自由度K=(5-3γ)/(γ-1)+1,ξ2=
宏观物理量与微观的分布函数的关系为

其中dΞ =d u d v d z dξ,dξ=dξ1dξ2…dξK,Ψ =(ψ1,ψ2,ψ3,ψ4,ψ5)=(1,u,v,z,(u2+v2+ξ2)/2).
由流体质量、动量、能量的守恒性,得到守恒约束条件

从BGK模型方程得到反应流体力学方程,同样可以利用Chapman-Enskog展开,零阶的Chapman-Enskog展开式f=g,代入方程(1),作矩得

其中Ψ =[1,u,v,z,(u2+v2+ξ2)/2],写成分量形式可得多组分的流体的Euler方程

其中总能量E=ρ[U2+V2+(K+2)/(2λ)]/2,压力P=ρ/(2λ).
若考虑化学反应,这时p=p(ρ,e,z),其中的z为组分变量,参数z由化学反应率方程确定

不同的化学反应类型有不同类型的表式,对理想流体的化学反应,一般取指数形式的Arrhenius反应率
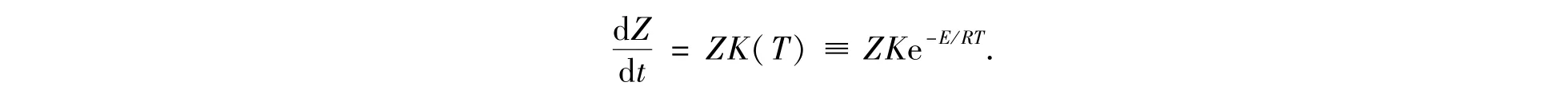
对于给定化学反应率的流体,与方程(2)对应的包含化学反应的流体力学方程为
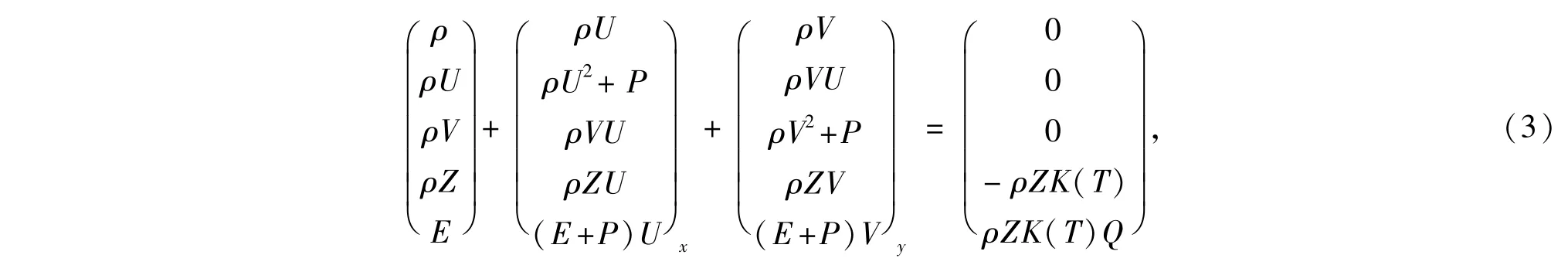
其中Q为化学反应的热能.
1.2 移动网格上的离散格式
对于含化学反应的无粘的可压缩的流体力学方程,为构造移动网格上的动理学数值方法,考虑运动控制体Ω(t),设其边界速度为Ug,则在Ω(t)上与方程组(3)对应的的积分形式可表示为
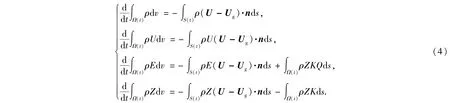
其中S(t)是控制体Ω(t)的边界,n是边界单位外法向,ρ,p,E和U=(U,V)分别为流体的密度,压强,比总能和速度.记e=E-U2/2为比内能.当Ug=0,方程组(4)是欧拉坐标的积分形式.当Ug=U时,则为拉氏坐标的积分形式.
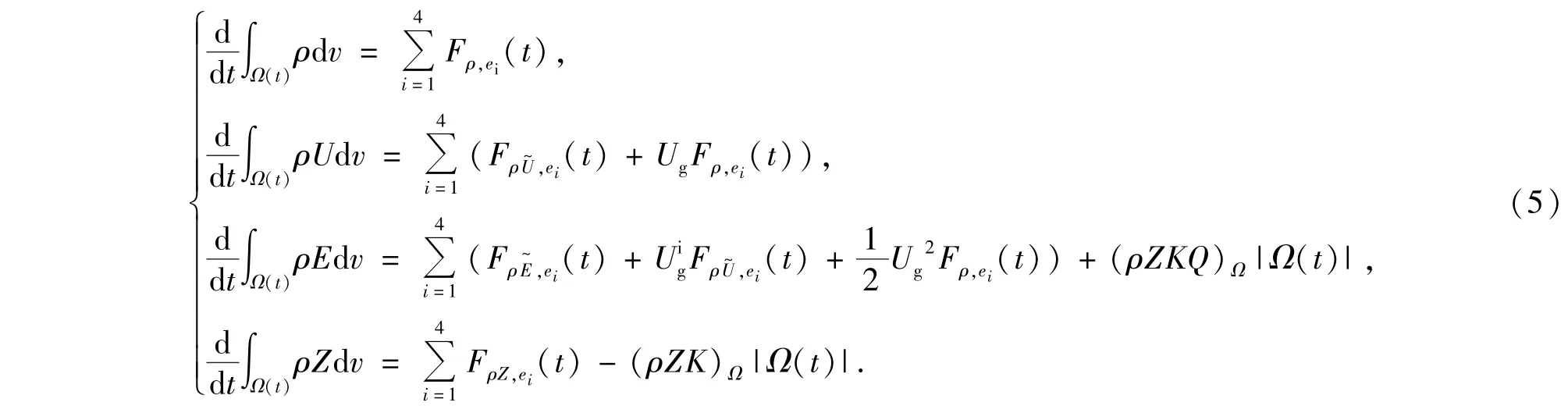
其中(·)Ω为Ω上的均值,

这里Fρ,ei,,Fρz,ei分别为通过边界ei的质量通量、动量通量和能量通量.
为得到分量形式的离散方程,将边界速度分解为法向与切向速度分量,记边界ei法向方向为n=(cosα, sinα),速度为U=(U,V),则法向速度′和切向速度分量为

则可将离散方程组(5)写为
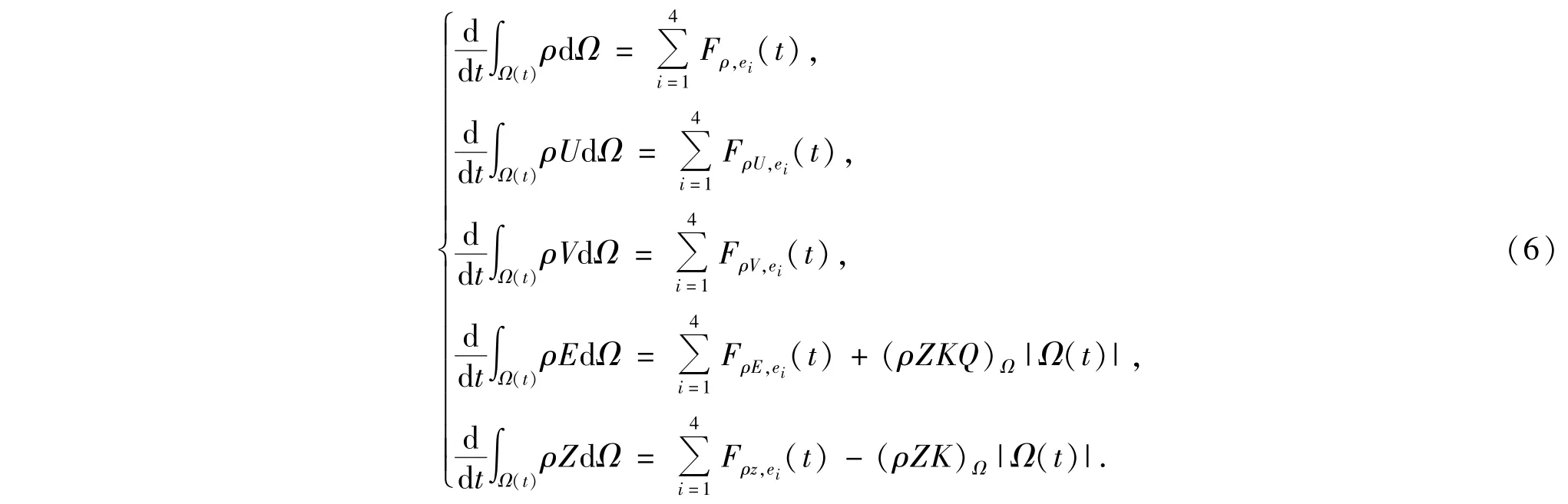
其中

方程组(6)是移动网格下有限体积半离散格式.定义不同时刻的控制体Ω′=Ω(tn+1)和Ω=Ω(tn),控制体上质量、动量和能量的质量平均值定义为

对半离散形式(6),由于动理学通量是时间的显函数,从时间步tn到tn+1积分,得到方程组(6)的全离散格式,时间离散是精确的.
1.3 动理学数值通量
在这一节,将利用方程(1)解的表达式构造数值通量,对于方向分裂格式,数值通量归结为一维的情形,与方程(1)对应的一维的BGK方程的解可表示为
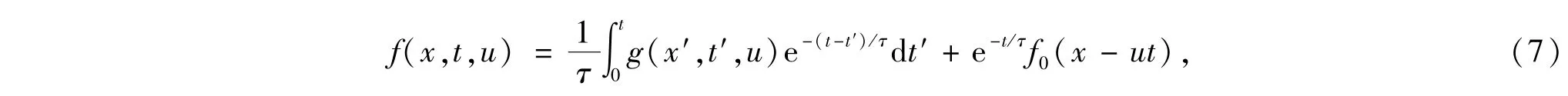
其中x′=x-u(t-t′).有了边界的分布函数,就能得到边界的数值通量,这样只需在边界点构造非平衡的初始分布f0与平衡分布函数g.
对非平衡的初始分布f0,不失一般性可设边界点xj+1/2=0,令
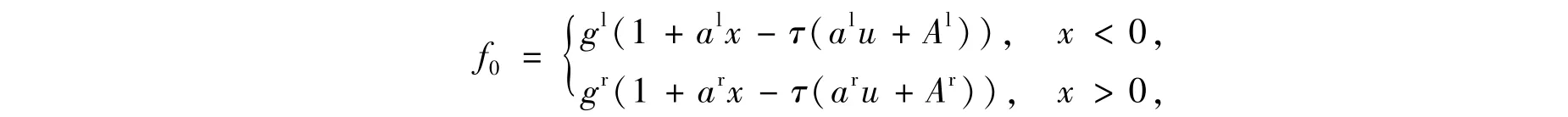
这里al,r,Al,r进一步可展开为

对于平衡态g,不妨设它为(x=0,t=0)附近的平衡态,可构造为

同样,

利用文献[19]中类似方法可计算出所有的系数.
将上述得到的非平衡的初始分布f0与平衡态分布g代入解的表达式(7),进行简单的积分运算可得

这样可以积分得到边界通量,
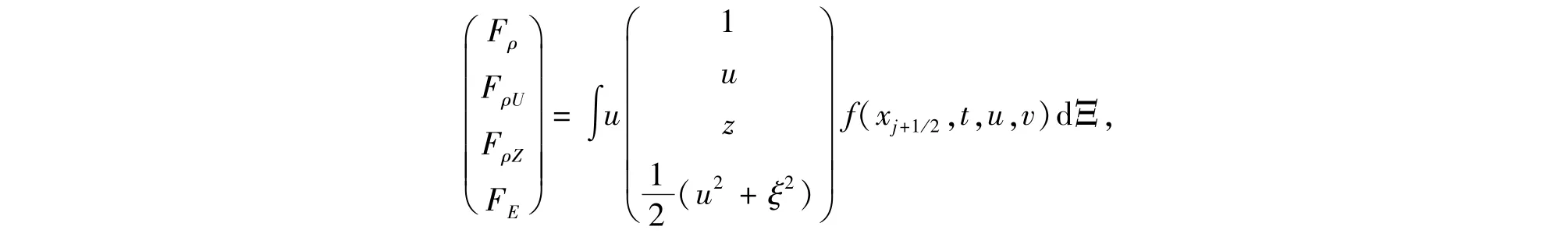
按边界法向与切向方向投影,再代入式(6)就可更新单元上的物理量.
1.4 网格移动速度
得到边界通量后,剩下就是要确定网格速度,为得到网格移动速度,只需要得到网格节点的新时刻的位置,利用
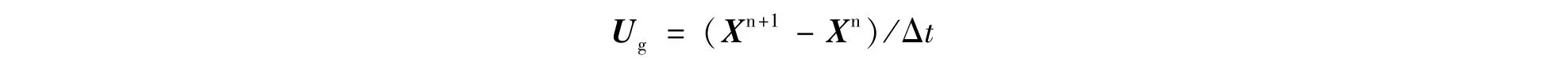
就可得到节点速度,其中Xn+1和Xn分别为新旧网格节点坐标,Δt是时间步长,利用线性关系就得到边界上各点的速度分布.
新时刻网格节点位置利用变分原理得到,假设x=x(ξ)是计算域到物理域的坐标映射,ξ=ξ(x)是逆映射.定义计算区域网格能量泛函为
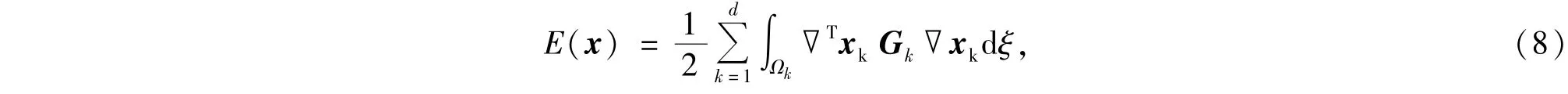
其中d是空间维数,Gk是给定的对称正定矩阵,为简单起见,这里取为Gk=w I,其中I是单位矩阵,w是非负加权函数.能量泛函(8)对应的欧拉-拉格朗日方程为
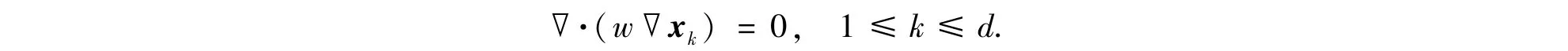
利用有限体积方法可得到网格移动方程的离散格式,参见文献[22],对二维的网格方程,权函数w取值为
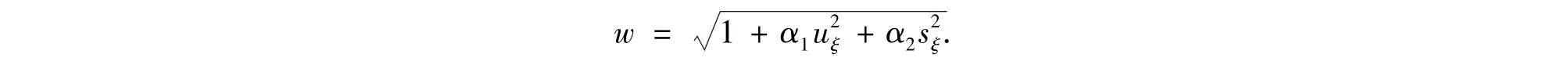
其中熵s=p/ργ,uξ为相应单元的物理量,α1和α2是可调非负参数.
2 数值实验
含化学反应的流体动力学行为比较复杂,实验结果很少,这里利用上节构造的数值方法给出几个典型算例的数值模拟结果.
一维反应流体数值实验
这是一个稳态的含化学反应的流体力学问题,激波前的状态为
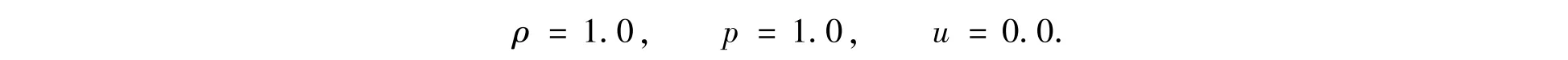
反应率中的参数分别为:Ea=14.0,Q=14.0,γ=1.4.波后状态利用下列公式计算[1],
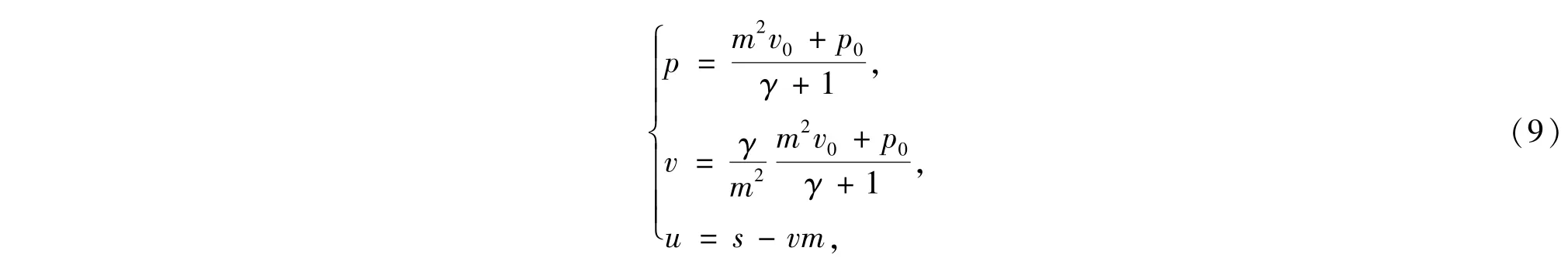

图1 密度的数值模拟结果与精确解Fig.1 Density comparison between exact solution (bold line)and numerical solution(circle)

图2 压力的数值模拟结果与精确解Fig.2 Pressure comparison between exact solution and numerical solution
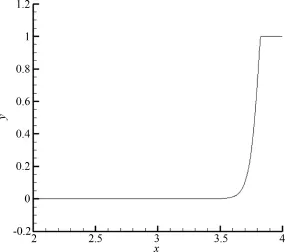
图3 质量分数的数值结果(未反应区的值为1.0,反应完成区为0.0.)Fig.3 Mass fraction distribution between 1.0 and 0.0
其中v=1/ρ,可得C-J状态的值
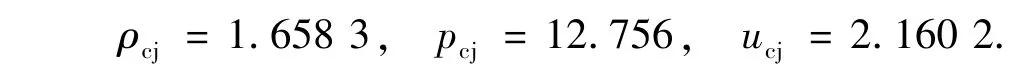
Von Newmann状态的值由公式
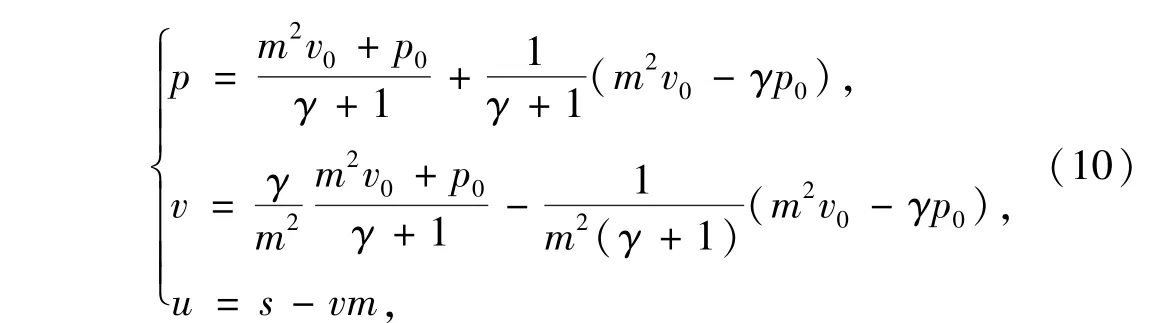
得到ρvn=4.852 1,pvn=24.512.其中
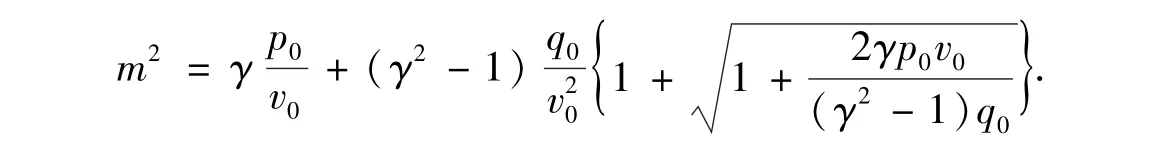
计算区域为[0,4],网格数为800,图1-2分别给出了密度与压力的数值结果与解析值的比较.图3为同一时刻的质量分数的数值结果,它表明这种数值格式有很高的分辨率.
二维反应流体的数值实验
这是非稳态的数值算例,计算区域为[0,4.0]×[0,1.0],网格数为480×120,冲击波由左至右传播,波前状态为ρ=1.0.p=1.0,u=0.0.冲击波波速为s=5.441 9,波后状态可以利用式(9)与(10)得到, y方向按正弦曲线作扰动,如图4为初始分布,图5为密度等值线图,图6则是相应时刻的局部网格分布.
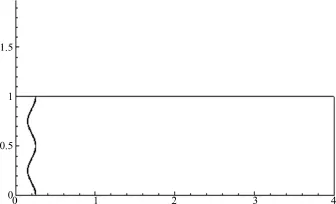
图4 二维初始分布(左右两侧均为分片常数,y方向为两周期的正弦扰动.)Fig.4 Initial distribution with piecewise constants

图5 密度等值线分布Fig.5 Distribution of density contours

图6 局部网格分布(显示的网格数为实际数量的1/10.)Fig.6 Localmesh distributions(1/10 meshes are shown.)
3 结论
利用BGK模型推导了含化学反应的流体力学方程组,构造了移动网格上离散格式,利用自适应移动网格方法得到网格速度,由动理学数值方法构造数值通量,这样得到了移动网格单元上新的物理量.一维与二维的数值实验表明这种格式同时具有高精度、高分辨率的特点.这种方法可以推广到一般状态方程的反应流体力学方程组.
[1] FickettW,DavisW C.Detonation[M].Berkeley:University of California Press,1979.
[2] Chapman D L.VI.On the rate of explosion in gases[J].Philosophical Magazine Series 5,1899,47(284):90-104.
[3] Jouguet JC E.On the propagation of chemical reactions in gases[J].Journal des Mathématiques Pures et Appliquées,Series 6,1905,1:347-425.
[4] Zel′dovich Y B.On the theory of the propagation of detonation in gaseous systems[J].Journal of Experimental and Theoretical Physics,1940,10:542-568.
[5] Neumann JV.Theory of detonation waves[R].Office of Scientific Research and Development,Report No.549,Ballistic Research Laboratory File No.X-122.Aberdeen Proving Ground,Maryland,1942.
[6] Döring W.On the detonation process in gases[J].Annals of Physics,1953,43:421-436.
[7] Kirwood JG,Wood W W.Structure of a steady state plane detonation wave with finite reaction rate[J].The Journal ofChemical Physics,1954,22:1915-1919.
[8] Erpenbeck JJ.Stability of idealized one reaction detonation[J].Physical Fluids,1964,7:684-696.
[9] 孙锦山,朱建士.理论爆轰物理[M].北京:国防工业出版社,1995.
[10] Hirt CW,Nichols B D.Volume of fluid(VOF)method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39(1):201-225.
[11] Glimm J,Grove JW,Li X,Zhao N.Simple front tracking[J].Contemporary Mathematics,1999,238:133-149.
[12] Hirt CW,Nichols B D.An arbitrary Lagrangian Eulerian computingmethod for all flow speed[J].Journal of Computational Physics,1997,135:203-216.
[13] Azarenok B N,Tang T.Second-order Godunov-type scheme for reactive flow calculations on movingmeshes[J].Journal of Computational Physics,2005,206:48-80.
[14] Harten A,Hyman J M.Self adjusting grid methods for one-dimensional hyperbolic conservation law[J],Journal of Computational Physics,1983,50:235-269.
[15] Ni G X,Jiang S,Xu K.Remapping-free ALE-type kinetic method for flow computations[J].Journal of Computational Physics,2009,228:3154-3171.
[16] Chapman S,Cowling TG.Themathematical theory of non-uniform gases[M].Cambridge University Press,1990.
[17] Mandal JC,Deshpande M.Kinetic flux vector splitting for Euler equations[J].Computers Fluids,1994,23(2):447-478.
[18] Chu C K.Kinetic-theoretic description of the formation of a shock wave[J].Physical Fluids,1965,8:12-22.
[19] Lei G,LiW,Ren Y.A high-order unstructured-gird WENO FVM for compressible flow computation[J].Chinese Journal of Computational Physics,2011,28(5):633-640.
[20] Xu X,Ni G.A high-ordermovingmesh kinetic scheme based on WENO reconstruction for compressible flows[J].Chinese Journal of Computational Physics,2013,30(4):509-514.
[21] Li Z,Yu X,Zhao G,Feng T.A RKDG finite elementmethod for Lagrangian Euler equation in one dimension[J].Chinese Journal of Computational Physics,2014,31(1):1-10.
[22] Xu K.A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method[J].Journal of Computational Physics,2001,171:289-335.
[23] Lian Y S,Xu K.Gas-kinetic scheme for multimaterial flows and its application in chemical reactions[J].Journal of Computational Physics,2000,163:349-375.
[24] Lian Y S,Xu K.Gas-kinetic scheme for reactive flows[J].Computers&fluids,2000,29:725-736.
[25] Tang H Z,Tang T.Adaptivemeshmethods for one-and two-dimensional hyperbolic conservation laws[J].SIAM Journal on Numerical Analysis,2003,41:487-515.
Adaptive M oving M esh K inetic Scheme for Reactive Fluids
ZHEN Yaxin1,2, NIGuoxi1
(1.LCP,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China;
2.School ofMathematics and Physics,North China Electric Power University,Beijing 102206,China)
We concern extension of gas-kinetic scheme of BGK type to reactive fluids,and develop an adaptivemovingmeshes BGK scheme(AMMBGK).We derive systems from amass fraction BGK model for detonation fluids,including both inviscid and viscous reactive flow systems.Then,based on a BGK type scheme and splitting method that splits system into fluid part and part of energy released from reaction process,we presentamass fraction BGK scheme onmovingmeshes for reactive flows.Numerical results validate availability of the gas-kinetic scheme in simulation of reactive fluids.
reactive fluids;mass fraction BGK model;gas kinetic scheme;adaptivemovingmeshes
1001-246X(2015)06-0677-08
O351
A
2014-11-04;
2015-02-02
国家自然科学基金(91130020,11402087),国防基础科研计划(B1520133015)及计算物理实验室基金资助项目
甄亚欣(1983-),女,博士,讲师,从事计算流体力学方法研究,E-mail:yasine_zhen@163.com

