基于ADAMS的对心曲柄滑块机构的运动学分析

潘鸣宇

（长春工业大学 机电工程学院，吉林 长春 130012）

0 引言

对心曲柄滑块机构能把回转运动转换为往复直线运动或作相反的转变，对它的研究和设计一直是机构学中的一个重要课题。合理地利用和改良曲柄滑块机构对提高工业产品的性能和功能、生产效率、产品的合格率等都有重大意义。本文将对曲柄与连杆等长的对心曲柄滑块机构进行运动学分析［1］，并实现参数化和可视化设计，在此基础上得到各运动参数的变化曲线，为曲柄滑块机构的改进和设计提供可靠的技术依据，简化含有对心曲柄滑块机构的机械装置的研发过程。

1 曲柄与连杆等长的对心曲柄滑块机构的数学模型

曲柄滑块机构由铰链四杆机构演化而成，该机构的刚性构件用低副（回转副、移动副）联接。曲柄滑块机构是由曲柄（或曲轴、偏心轮）、连杆、滑块通过移动副和转动副组成的系统［2－3］，运动主体部分为曲柄与连杆组成的臂状机构，其运动状态与平面2R机器人相似。在机器人动力学中机器人由连杆和关节组成，D－H法可以表示不同连杆组成的机器人在任何坐标中的运动状态，在D－H法中，对每一关节指定一个参考坐标系，并且确定从第n－1关节到第n关节（一个坐标系到下一个坐标系）进行变换的步骤。若对从基座到第1关节、再从第1个关节到第2个关节依此类推到第n关节的所有变换进行n次的相应矩阵运算，可得出机器人包含的n个连杆的总变换矩阵。将曲柄和连杆简化为机器人中的连杆及其关节，沿曲柄建立附体坐标系，如图1所示。设该机构中构件曲柄为连杆1，构件连杆为连杆2。根据D－H表示法确定连杆每个关节的参考坐标系，其中曲柄O0O1的铰接点为O0，设为第0坐标系；曲柄O0O1与连杆O1O2的连接点为O1，设为第1坐标系；连杆O1O2末端即滑块为点O2，设为第2坐标系。然后分别求解出实现第0坐标系与第1坐标系、第1坐标系与第2坐标系之间的变换矩阵，最后将两个变换矩阵相乘可求解出总变换矩阵，既可得出连杆2末端位姿。

图1 曲柄与连杆等长的对心曲柄滑块机构简化模型

在得到末端位姿的前提下将其对时间求导可得雅克比矩阵，进而可得到相应点的速度矢量与关节速度矢量，最后整理可以得到关节角加速度与末端加速度之间的数学关系，即该曲柄与连杆等长对心曲柄滑块机构的运动学方程：

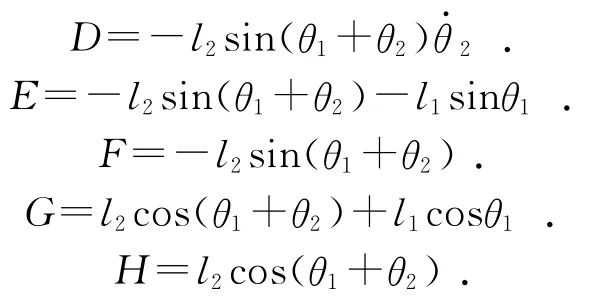
2 利用ADAMS建立三维模型

ADAMS软件自身具有一定的三维建模功能，在此研究中可以使用简单的模型表达该机构的运动原理，故不需要将其他CAD软件制作的数模对ADAMS进行导入［4］。首先建立如图2所示的对心曲柄滑块运动原理图，假定曲柄与连杆长度都为30cm，使用连杆功能建立曲柄与连杆，以坐标原点（0，0，0）为曲柄铰接点建立OA（PART＿2），用位置功能使PART＿2与X轴呈45°，再以PART＿2上的MARKER＿2为铰接点建立连杆AB（PART＿3），用位置功能使其与PART＿2呈90°得到等腰直角三角形；用长方体功能在PART＿3上的MARKER＿4上建立滑块（PART＿4），用位置功能使其中心与MARKER＿4重合，得到如图3所示的三维模型。然后在MARKER＿1处对曲柄与ground、在MARKER＿2处对连杆与曲柄、在MARKER＿4处对滑块与连杆分别使用旋转副功能建立旋转关系，对滑块与ground使用滑动副功能建立滑块在X轴上的水平位移关系，建立滑动副时需要选择MARKER＿4与MARKER＿1来确立位移方向来保证水平移动［5］。

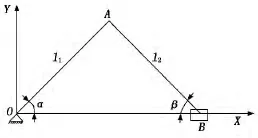
图2 对心曲柄滑块运动原理

3 运动仿真

3.1 运动仿真的建立

图3 对心曲柄滑块机构的简化三维模型

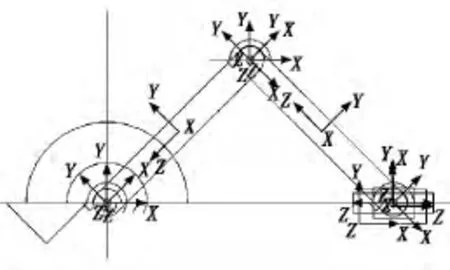
图4 驱动设定完毕的三维模型

3.2 仿真结果

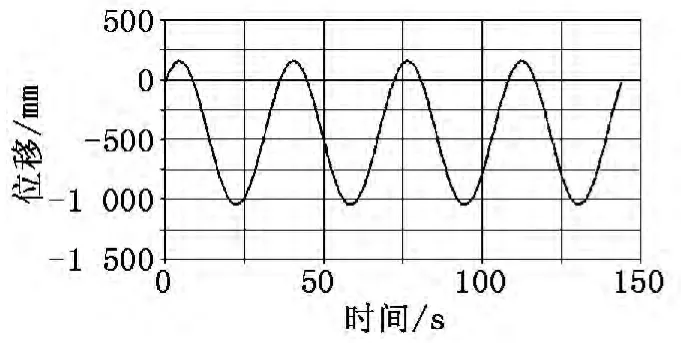
图5 滑块位移曲线

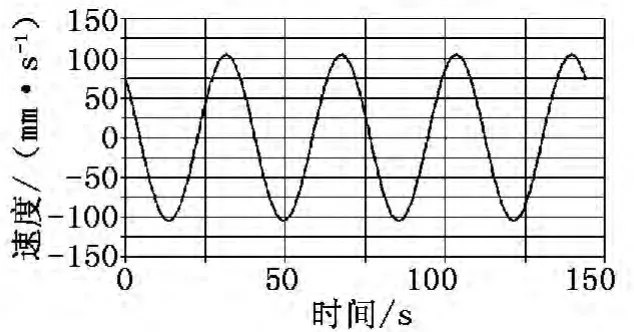
图6 滑块速度曲线

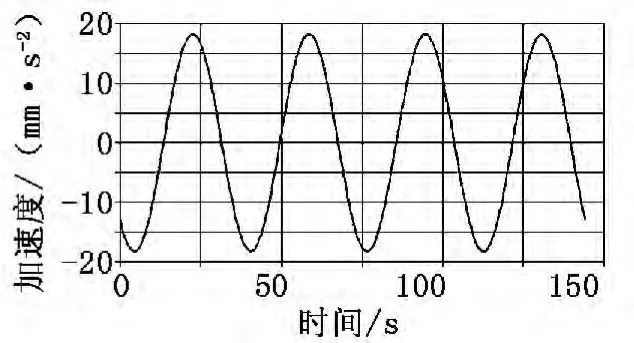
图7 滑块加速度曲线

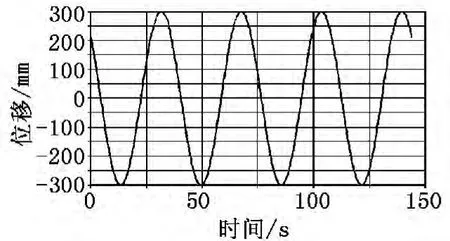
图8 MARKER＿2在Y轴的位移

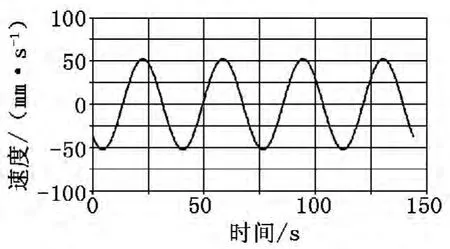
图9 MARKER＿2在Y轴的速度

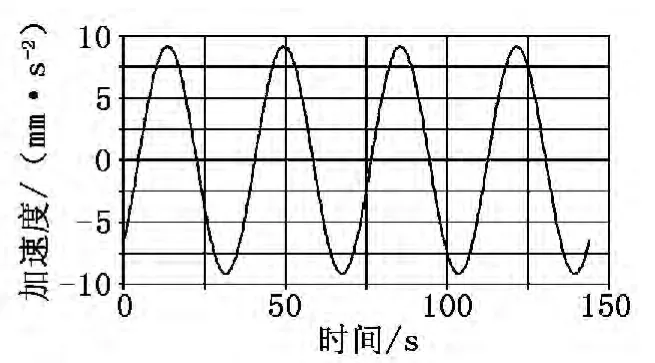
图10 MARKER＿2在Y轴的加速度

4 结论

利用机器人运动学中的D－H法建立了曲柄滑块机构中曲柄和连杆的同一坐标系运动方程，使用ADAMS软件对对心曲柄滑块机构进行了运动学仿真分析，并得到了相应运动曲线。重点分析了曲柄滑块机构在机械装备中常用的几个构件的运动状态，完成了预期的仿真目的。使用ADAMS进行参数化设计和仿真可大大简化和完善机构的运动分析方法，为众多机械装备的改进提供良好平台。

图11 MARKER＿2的运动轨迹

［1］黄经元，王淑芳，贾颖莲，等.基于Pro/E的发动机曲柄滑块机构的运动仿真分析［J］.制造业自动化，2010（6）：163-165.

［2］高晓红，褚金奎，郭晓宁.齿轮连杆机构力分析与运动分析［J］.西安理工大学学报，2002，18（3）：289-293.

［3］张策.机械动力学［M］.北京：高等教育出版社，2000.

［4］李军，邢俊文，覃文洁，等.ADAMS实例教程［M］.北京：北京理工大学出版社，2002.

［5］段钦华，杨实如.曲柄滑块机构动力学参数优化设计［J］.成都大学学报，2002，21（3）：18-23.

［6］葛军，刘英林.基于ADAMS的蜗轮蜗杆传动机构的仿真研究［J］.机械工程与自动化，2010（12）：74-75.