基于广义似然比的小波域SAR图像相干斑抑制算法

基于广义似然比的小波域SAR图像相干斑抑制算法

侯建华，刘欣达，陈稳，陈少波

(中南民族大学 电子信息工程学院，武汉430074)

摘要在联合检测与估计理论框架下推导出了Bayes萎缩函数表达式，并提出了一种基于广义似然比的小波域SAR图像去斑算法.该算法对含斑SAR图像直接做冗余小波变换，求出小波系数所对应的二值掩模；对相干斑噪声和有用信号的似然条件概率分别建模为尺度指数分布和Gamma分布，根据二值掩模信息，采用最大似然估计得到两种模型的参数并计算似然条件概率比.实验结果表明：文中所给算法在有效滤除斑点噪声的同时，也较好地保持了图像的细节信息，在对人工加斑图像和多幅实际SAR图像的处理中获得了令人满意的结果.

关键词联合检测与估计；SAR图像去斑；小波变换；广义似然比

收稿日期2015-01-20

作者简介侯建华(1964-)，男，教授，博士，研究方向：图像处理、模式识别，E-mail：hou8781@126.com

基金项目国家自然科学基金资助项目(61141010， 61201448)；湖北省自然科学基金资助项目(2012FFA113)

中图分类号TN911.73文献标识码A

Generalized Likelihood Ratio Based SAR Image

Speckle Suppression Algorithm in Wavelet Domain

HouJianhua,LiuXinda,ChenWen,ChenShaobo

( College of Electronic Information Engineering, South-Central University for Nationalities, Wuhan 430074, China)

AbstractA Bayes shrinkage formula is derived under the framework of joint detection and estimation theory, and a wavelet SAR image despeckling algorithm is realized based on generalized likelihood ratio. Firstly, redundant wavelet transform is performed directly to the original speckled SAR images, and binary mask is obtained for each wavelet coefficient. We use scale exponential distribution and Gamma distribution, respectively, to model the likelihood conditional probability of speckle noise and useful signal. According to the mask, the parameters of the two modes are estimated by maximum likelihood estimation method, and thus the likelihood conditional probability ratio is calculated. Experiment results show that the proposed method can effectively filter the speckle noise, and at the same time preserve the image details as possible. Satisfactory results are achieved on both synthetically speckled images and real SAR images.

Keywordsjoint detection and estimation；SAR image despeckling；wavelet transform；generalized likelihood ratio

合成孔径雷达(SAR)在卫星遥感领域得到广泛的应用，但由于SAR的相干成像机理，SAR图像所固有的相干斑噪声严重降低了SAR图像的可解译程度，影响了后续的图像处理任务，因此相干斑抑制方法研究成为SAR图像预处理中一个非常重要的部分.SAR图像去斑方法最初采用的是简单空间域滤波方法，如均值滤波和中值滤波；从20世纪80年代开始到90年代初期，提出了空域自适应滤波算法，典型代表为Lee滤波器[1]、Kuan滤波器[2]、Gamma MAP 滤波器[3,4]等；这些算法通过在图像上取一个滑动窗,以窗内所有像素作为滤波器的输入值,基于窗口内的局部统计特性进行滤波处理，获得了优于均值滤波和中值滤波的效果.

从20世纪90年代Donoho等人将小波分析应用于图像去噪开始[5],小波域去斑算法研究已成为SAR图像去斑的主流方向[6-8].基于小波的SAR图像去斑算法中研究最多的是小波阈值或萎缩方法，但这种方法没有充分考虑斑点噪声小波系数的统计特性；并且选取适当的阈值也始终是一个难题.

为了进一步提高算法的去斑性能，近年来，利用SAR图像小波系数的统计分布特性,结合贝叶斯统计理论的SAR图像去斑已成为该领域的一个研究热点.Xie等提出了基于马尔可夫随机场的小波域贝叶斯斑点消除方法[9]；Achim等将真实信号所对应的小波系数视为alpha-stable分布，斑点系数为高斯分布，利用贝叶斯最大后验概率技术(MAP)对SAR图像进行估计[10]；文献[11]将有用信号、斑点噪声的系数分别建模为拉普拉斯分布、瑞利分布，利用Bayesian MAP准则得到了解析的软阈值去噪表达式.在基于小波统计模型的SAR去斑方法中，关键问题是如何对其中的有用信号和斑点噪声信号建模，以及如何有效地对真实的信号做出估计，这些方面还有大量的工作有待于探索.

本文在文献[12]的基础上，实现了一种快速、有效的SAR图像去斑算法.该方法没有采用常规的对数变换，而是直接对SAR图像做冗余小波分解，然后利用分类技术将小波系数划分为两类；其中斑点噪声系数建模为尺度指数分布，有用信号的系数则建模为Gamma分布；根据Bayes最大似然估计得到这两种模型的参数；最后基于联合检测与估计理论的广义似然比(generalized likelihood ratio)框架，得到自适应的萎缩函数表达式.

1基于广义似然比的Bayes去斑理论

文献[13]指出：在雷达信号处理、语音传输过程中，判断系统观察空间中的某一点是否代表信号，这个问题往往是不确定的.为此文献[13]提出了信号的联合检测与估计理论，该理论已成功应用于语音信号处理中.本文就是将联合检测与估计的方法应用于小波域SAR图像去斑.

1.1符号

为了清楚起见，先对符号做统一说明.设wk,,j,D表示原始SAR图像在空间位置为k，分辨率尺度为j，图像细节方向为D的小波系数，其去斑后相应的估计值为yk,,j,D.下面在不至于混淆的情况下忽略尺度和方向标记j、D.

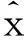
1.2Bayes萎缩函数

根据联合检测与估计理论[13,14]，设H1表示假设“小波系数对应的是信号”，H0表示假设“小波系数对应的是噪声”.则真实信号的概率密度为：

p(y)=p(H0)·p(y|H0)+p(H1)·p(y|H1),

(1)

y的最小均方误差估计(MMSE)为：

E(y|w)=p(H0|w) ·E(y|w,H0)+p(H1|w)·E(y|w,H1),

(2)

下面对(2)式化简[14].首先，在H0假设成立的条件下，E(y|w,H0)≈0 ，则(2)式简化为：

E(y|w)≈p(H1|w)·E(y|w,H1),

(3)

进一步，在H1假设成立的条件下，E(y|w,H1)≈y，则(3)式简化为下面的萎缩函数形式：

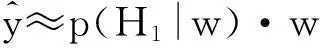
(4)

在(4)式的具体实施中，用后验概率p(Xk=1|Mk=mk)代替p(H1|w).考虑到位置k处的该后验概率既与全局先验有关(这里的全局先验是针对一个子带而言的)，也与位置k处的局部邻域信息有关[14]，因此在计算后验概率p(Xk=1|Mk=mk)过程中引入k点的邻域信息，得到：

y=p(Xk=1|Mk=mk,X∂k)·w.

(5)

下面推导后验概率p(Xk=1|Mk=mk,X∂k)·w的表达式.根据Bayes公式:

p(Xk=1|Mk=mk,X∂k)=

(6)

上式推导中做了Mk=mk与X∂k相互独立的假设，其中:

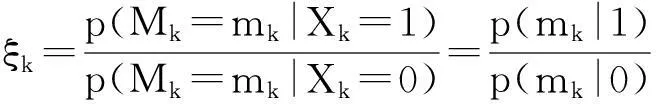
(7)

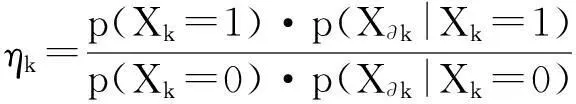
(8)

ξk与ηk的乘积ξk·ηk称为广义似然比.ξk代表似然条件概率之比，其计算依赖于具体的条件概率模型，将在下面讨论.ηk代表先验信息，文献[12]利用吉布斯随机场(GRF)模型，提出了一种计算ηk的方法：

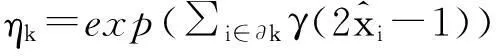
(9)

其中参数γ控制邻域系数对算法的影响.最终得到的基于广义似然比的萎缩函数表达式为：

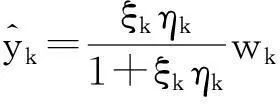
(10)

2广义似然比的计算

根据(10)式，ηk可以通过当前位置的邻域信息得到，关键是似然条件概率比ξk的计算.其思想是首先估计每个位置所对应的二值掩模；再对两种假设下的小波系数的条件概率密度建模，结合掩模对模型参数进行估计，最后得到两种假设下的条件概率密度，从而计算出ξk.

2.1掩模估计

图像经过冗余小波分解，每一个小波子带都具有相同的尺寸.根据小波系数的尺度传递性，有用信号(如图像边缘)小波系数的幅度随着分解尺度的增加而增加，而表示噪声的小波系数正好系数则相反.利用该性质，在尺度j的每个细节子带wj,D中，按下式对二值掩模标记进行估计：

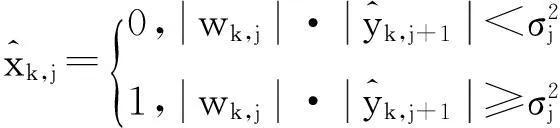
(11)

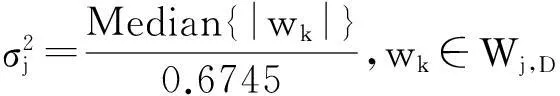
(12)

2.2似然函数估计

图1是真实的SAR图像(horsetrack)第1尺度HL1子带中m0、m1的直方图(实线)，即经验似然函数p(mk|0)和p(mk|1).

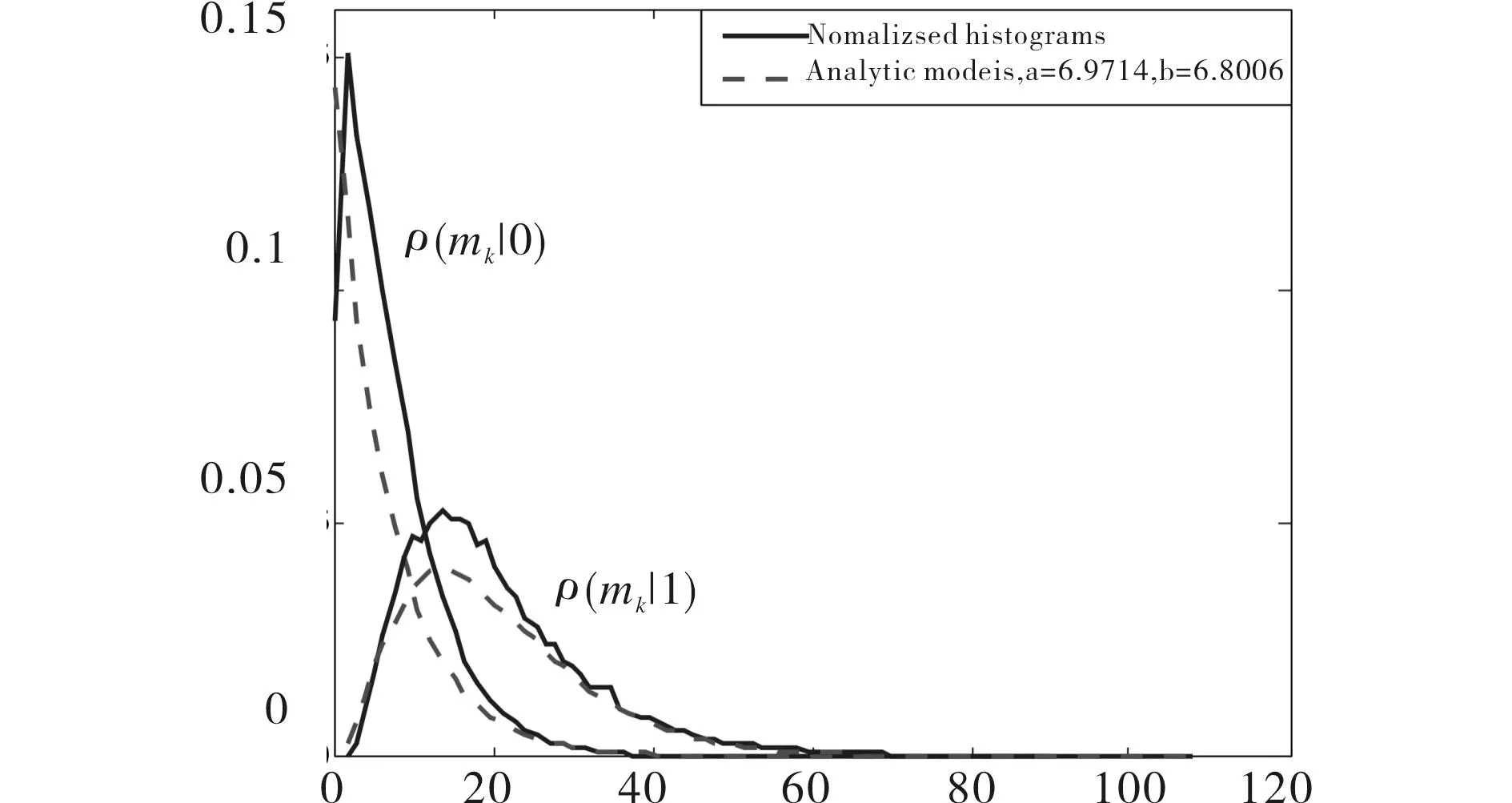
图1　horsetrack图像HL1子带的经验似然函数估计 (实线)和分析模型曲线(虚线) Fig.1　Empirical likelihood estimation in HL1 subband of horsetrack image(solid line) and the analysis model curve (dashed line)

由图1，文献[12]提出用尺度指数分布、广义Gamma分布分别近似斑点噪声系数、有用信号的系数m0、m1的经验似然函数，从图中可以看到，这两种理论模型能够较好的模拟实际直方图分布.这两种分布的概率密度函数分别为：

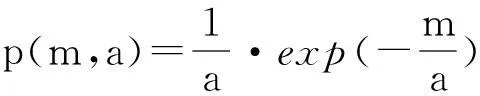
(13)

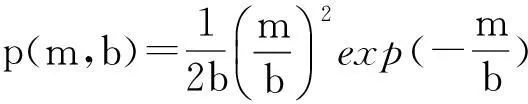
(14)

先假设模型参数a、b已知，于是广义似然比为：

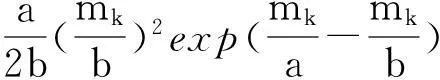
(15)

根据(10)式就可得到基于广义似然比的萎缩函数表达式.

2.3模型参数估计

上面的两种概率分布都只有一个参数，在给定观测数据条件下利用最大似然估计(ML)理论可以很容易地求出各自的模型参数.

对于尺度指数分布，令θ=1/a，则(13)式写为：p(m,θ)=θ·exp(-θm)；

在给定观测数据m0=(m1,m2,…,mn0)条件下，联合概率密度为：

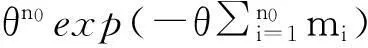
(16)

相应的对数似然函数为：

(17)

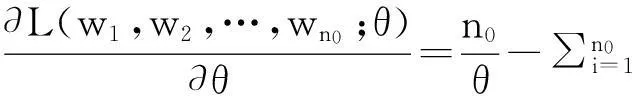
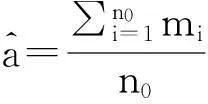
(18)

同理，广义Gamma分布模型参数b的参数的最大似然估计:

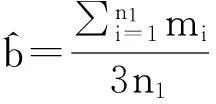
(19)

其中n0、n1分别是m0、m1的长度.

图1同时给出了两种分析模型对实际直方图的拟合(虚线)，其中参数a、b按照(18)、(19)式计算.从图1可见，尺度指数分布和广义Gamma分布可以较好地表示m0、m1的条件概率密度函数.

3去斑算法步骤

上述完整的小波域SAR图像去斑算法步骤如下.

1) 对含斑图像做N层冗余小波分解；

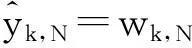
3) 对j=1,2，…,N-1尺度的各方向子带：

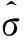
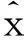
iii) 按(18)、(19)式估计模型参数a、b；

iv) 由(15)式计算ξk，由(9)式计算ηk；

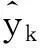
4) 做小波反变换，得到去斑后的恢复图像.

具体应用中，使用二次样条小波，做4尺度冗余小波分解.

4实验结果

4.1参与实验的算法说明

我们选取了另外4种常用的算法与本文算法比较：

(1)传统均值滤波；

(2)同态Wiener滤波[15]，该方法是在空域对图像做对数变换后再进行Wiener滤波，最后做指数变换；

(3)增强型Gamma MAP滤波器，该方法被认为是目前空域自适应滤波方法中最好的算法之一，在近年来的相干斑去噪文献中通常被做为标准算法与其它方法进行比较[14]；

(4)BayesShrink软阈值去噪算法[16]，记为BayesShrink-RWT；但与文献[16]不同的是，这里要先对图像做对数变换后再进行BayesShrink软阈处理，最后做指数变换；并且常用冗余小波变换，它比基于正交小波的BayesShrink算法具有更好的去斑性能.

(5)本文方法，考虑邻域信息，即根据(9)式计算ηk，其中γ取值为0.2，窗口为3×3.

4.2实验结果与分析

首先在人工加斑图像(即模拟SAR图像)上对各种去斑方法进行比较，然后给出针对真实SAR图像的实验结果和分析.采用客观评价与主观评价相结合的方法综合衡量算法的去斑性能，其中客观评价指标为等效视数(ENL)；等效视数是衡量一幅SAR图像相干斑噪声相对强度的一种指标.等效视数越大,表明图像上的相干斑越弱,可解译性越好.等效视数可以由SAR图像中一块均匀区域I的均值平方与方差的比值计算，其定义为：

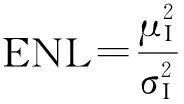
(20)

其中μ与σ分别是SAR图像中一块均匀区域内的均值与标准差.

表1给出了在模拟Lena斑点图像上的性能比较，图2是各种算法的视觉效果比较.

表1不同去斑算法在模拟Lena斑点图像上的性能比较

Tab.1Performance comparison of different despeckling

algorithm in Lena synthetically speckled image

去斑算法等效视数(ENL)斑点图像19.12均值滤波161.76同态Wiener滤波151.21增强型Gammaf滤波161.76BayesShrink软阈值256.47本文方法177.77

从表1可以看出，本文算法的等效视数仅比BayesShrink软阈值方法低，高于其它三种算法.但从图2给出的去斑后视觉效果考察，BayesShrink软阈值方法处理后的图像过平滑现象比较严重，其它三种算法处理后的图像则还存在一些明显的斑点噪声；相比之下，从视觉效果上看，本文算法在去斑与保持图像细节之间的择中方面具有显著的优势.

真实SAR图像选自Sandia Natioanal Laboratories，分别是horse track (396×600)、agricultural field (350×600)、China Lake Airport (686×532).实验结果见表2和图3.

图2　不同去噪算法在模拟Lena斑点图像(SNR=11.75)上滤波后的视觉效果比较 Fig.2　Visual comparison of different despeckling algorithms on synthetically speckled image Lena (SNR=11.75)

去斑算法HorsetrackAgriculturalChinaLackAirport原始斑点图像15.9413.8623.43均值滤波76.6659.0872.97同态Wiener滤波73.3051.1464.55增强型GammaMAP滤波76.6659.3371.13BayesShrink软阈值去噪61.1545.7363.53本文算法121.85106.03118.11

图3　本文算法对不同真实SAR图像的去斑效果 Fig.3　Despecking effects of the proposed method on different real SAR images

从表2和图3中可看出该算法能够有效地滤除斑点噪声，同时图像的强、弱细节得以较好地保持.由此可见本文算法在对人工加斑图像和多幅实际SAR图像处理中都获得了令人满意的结果.

5结语

本文基于联合检测与估计的理论框架，设计并实现了一种基于广义似然比的小波域SAR图像去斑算法.该方法通过二值掩模将小波系数划分为两类：有用信号和斑点噪声信号，利用实际SAR图像小波系数的统计分布特性，分别对这两类信号进行建模并求出模型参数，最终根据所推导的Bayes萎缩函数对SAR图像做去斑处理.实验结果表明，本文算法能有效地抑制斑点噪声、同时又能较好的保持图像的纹理细节和边缘信息，能够满足后续图像处理任务的要求.

参考文献

[1]Lee J S. Refined filtering of image noise using local statistics[J]. Computer graphics and image processing, 1981, 15(4): 380-389.

[2]Kuan D T, Sawchuk A A, Strand T C, et al. Adaptive noise smoothing filter for images with signal-dependent noise[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1985 (2): 165-177.

[3]Kuan D T, Sawchuk A, Strand T C, et al. Adaptive restoration of images with speckle[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(3): 373-383.

[4]Lopes A, Nezry E, Touzi R, et al. Structure detection and statistical adaptive speckle filtering in SAR images[J]. International Journal of Remote Sensing, 1993, 14(9): 1735-1758.

[5]Donoho D L. Ideal spatial adaptation via wavelet shrinkage[J]. Biometrica, 1994, 81: 424-455.

[6]侯建华. 基于小波及其统计特性的图像去噪方法研究 [D]. 武汉: 华中科技大学, 2007.

[7]Argenti F, Lapini A, Bianchi T, et al. A tutorial on speckle reduction in synthetic aperture radar images[J]. IEEE Geoscience and Remote Sensing Magazine, 2013, 1(3): 6-35.

[8]侯建华, 毛晓晖. 基于正态反高斯先验模型的小波去噪算法[J]. 中南民族大学学报: 自然科学版, 2009 (3): 85-89.

[9]Xie H, Pierce L E, Ulaby F T. SAR speckle reduction using wavelet denoising and Markov random field modeling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(10): 2196-2212.

[10]Achim A, Tsakalides P, Bezerianos A. SAR image

denoising via Bayesian wavelet shrinkage based on heavy-tailed modeling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(8): 1773-1784.

[11]Jian-Hua Hou, Xiang-Ming Liu, Cheng-Yi Xiong,

Xiang He. Speckle reduction algorithm for synthetic aperture radar images based on Bayesian maximum a posteriori estimation in wavelet domain [J]. Optical Engineering, 2008, 47(5): 057004-1 — 057004-11.

[12]Pizurica A, Philips W, Lemahieu I, et al. Despeckling SAR images using wavelets and a new class of adaptive shrinkage estimators[C]//IEEE.Proceedings of International Conference on Image Processing. San Francisco: IEEE, 2001, 2: 233-236.

[13]Middleton D, Esposito R. Simultaneous optimum detection and estimation of signals in noise[J]. IEEE Transactions on Information Theory, 1968, 14(3): 434-444.

[14]Pizurica A. Image denoising using wavelets and spatial context modeling[D]. Ghent : Ghent University, 2002.

[15]Achim A, Bezerianos A, Tsakalides P. Novel Bayesian multiscale method for speckle removal in medical ultrasound images[J]. IEEE Transactions on, Medical Imaging, 2001, 20(8): 772-783.

[16]Chang S G, Yu B and Vetterli M. Adaptive wavelet thresholding for image denoising and compression[J]. IEEE Transactions on Image Processing, 2000, 9(9): 1532-1546.