带诺依曼边界的非局部问题非平凡解的存在性

带诺依曼边界的非局部问题非平凡解的存在性

周静,殷红燕

(中南民族大学 数学与统计学学院，武汉 430074)

摘要主要考虑一类带诺依曼边界的分数阶薛定谔方程的非平凡解的存在性，通过直接计算我们得到非局部算子的分部积分公式和格林公式.该问题具有变分结构.通过验证该问题满足山路引理条件，证明了该问题存在非平凡解的结论．

关键词诺依曼问题；分数阶非线性薛定谔方程；非局部法向导数；非平凡解

收稿日期2014-10-27

作者简介周静(1982-)，女，讲师，研究方向：非线性偏微分方程，E-mail:zhouj@mail.scuec.edu.cn

基金项目中央高校基本科研业务费专项资金资助项目(CZQ13017)

中图分类号O175文献标识码A

The Existence of Nontrivial Solution of a Nonlocal

Problem with Neumann Boundary

ZhouJing,YinHongyan

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)

AbstractThe main purpose of this paper is to investigate the existence of nontrivial solution of a Neumann type problem for fractional Schrodinger equations.Through direct computation, we obtain the integration by parts formula and Green′s identity.The problem has a variational structure.Through verifying the problem satisfying the Mountain pass theorem, we prove the existence of nontrivial solution of this problem．

KeywordsNeumann problem；fractional nonlinear Schrodinger equation；nonlocal normal derivative；nontrivial solution

本文主要考虑如下分数阶非线性方程：

(1)

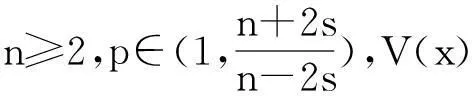
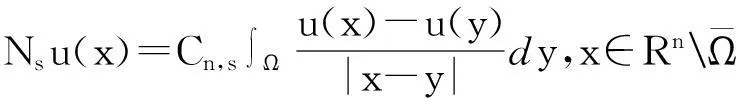
这里Cn,s是对应于分数阶拉普拉斯算子(-Δ)s的标准化常数，满足：

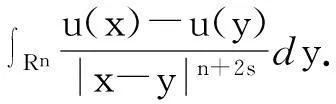
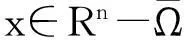
在本文给出主要结果之前，先来回顾关于经典条件下的一些工作，奇异的带诺依曼边界条件的次临界指标的非线性薛定谔方程如下：

(2)

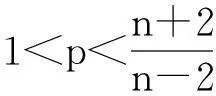
1记号与预备知识

分数阶微分方程是许多工程和物理问题中的抽象形式，在分形和多孔介质的弥散、电解化学、半导体物理、凝聚态物理、粘弹性系统、生物数学及统计学等学科中有重要的应用，从而使得分数阶微分方程的研究得以飞速发展. 分数阶微积分理论主要研究任意阶数的微分、积分算子的特性及应用，其发展几乎与整数阶微积分理论同步，是整数阶微积分理论的延伸，而分数阶微分算子与整数阶微分算子最主要的区别在于：分数阶微分算子为非局部算子而整数阶微分算子为局部算子.

分数阶拉普拉斯算子中的s,s∈(0,1)是一个带有|ξ|2s的伪梯度算子，精确的说：

(-Δ)su=F-1(|ξ|2sF(u)(ξ)),

(3)

其中F为傅里叶变换.设u∈H2s(Rn),那么由(3)式所定义的分数阶拉普拉斯算子与下面的公式等价[2]：

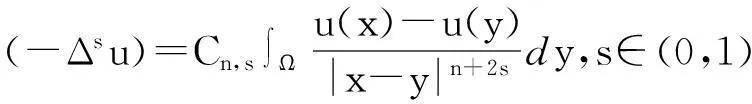
其中Cn,s是单位化常数.

记γ(x,y)=Cn,s|x-y|-(n+2s).定义：

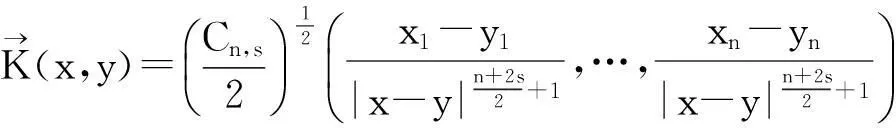
注意到K(x,y)=-K(y,x)，且2K(x,y)·K(y,x)=γ(x,y).

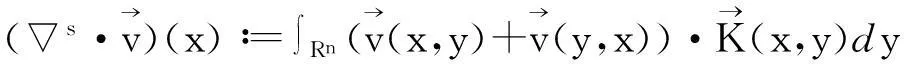
x∈Rn.

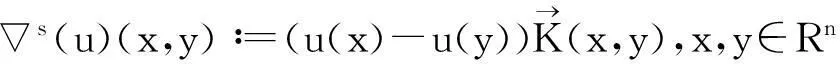
通过直接计算不难得出[1],s满足：

定义3对应于分数阶拉普拉斯算子的交互算子N定义为：

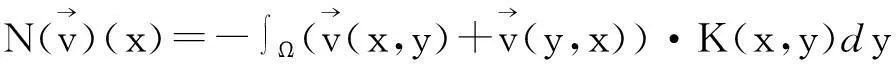
x∈Ωc.

由以上定义我们可以推导出如下高斯型公式和分部积分公式：

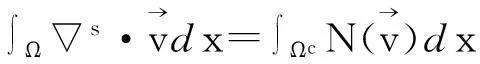
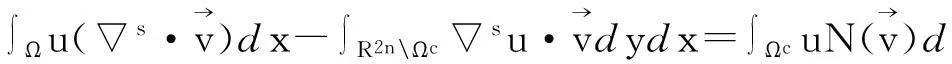
∫Ωv(-Δ)sudx=∫R2nΩcsu·svdydx-

本文所考虑的问题具有变分结构，令：

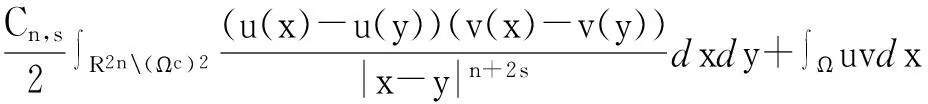
定义空间Hs(Ω)={u:Rn→R可测，且u,vHs(Ω) <∞}，它为Hilbert空间,范数为‖·‖2=·,·Hs(Ω) ，详见文献[1]中命题3.1 g=0,ε=1 的情形．由索伯列夫定理可知，在Hs(Ω)上可以定义等价范数：

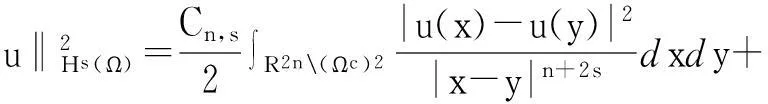
∫ΩV(x)u2dx.

显然问题(1)的弱解为如下泛函的临界点：

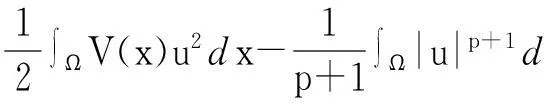
若u∈Hs(Ω)是问题(1)的弱解，则对任意的v∈Hs(Ω)，有：

∫R2n(Ωc)2(su·sv)(x,y)dxdy+

∫ΩV(x)uvdx-∫Ω|u|p-1uvdx=0.

(4)

由格林公式有：

∫R2n(Ωc)2(su·sv)(x,y)dxdy=

∫Ωv(-Δ)sudx-∫ΩcvN(su)dx,

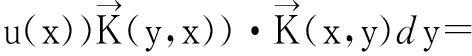
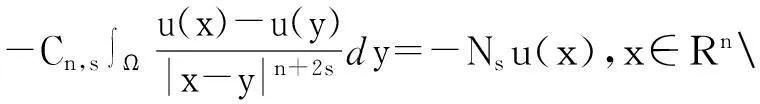
最后一步具体由文献[2]可得.从而(4)式变成：

∫Ω((-Δ)su+V(x)u-|u|p-1u)vdx-

∫ΩcvNsudx=0.

2主要结果及证明

引理1I的临界点是问题(1)的解.

证明对任意的v∈Hs(Ω),有：

I(u+tv)=I(u)+t(∫R2n(Ωc)2(su·sv)(x,

y)dxdy+∫ΩV(x)uvdx-∫Ω|u|p-1uvdx)+

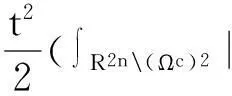
p∫Ω|u+θtv|p-1v2dx).

其中θ∈(0,1)，所以：

∫R2n(Ωc)2(su·sv)(x,y)dxdy+∫ΩV(x)uvdx-

∫Ω|u|p-1uvdx=u,vHs(Ω) -∫Ω|u|p-1uvdx.

从而可知若u∈Hs(Ω)是I的临界点,那么u∈Hs(Ω)是问题(1)的弱解.

引理2I满足PS紧性条件.

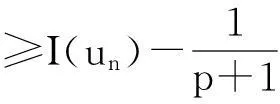
从而有‖un‖有界.

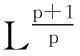
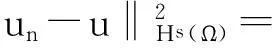
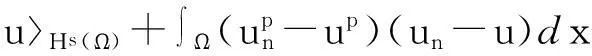
显然有：

I′(un)-I′(u),un-uHs(Ω) →0,n→∞.

由索伯列夫不等式可得：

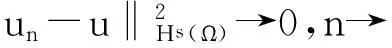
引理3I满足山路引理结构.

证明由引理1可知泛函：

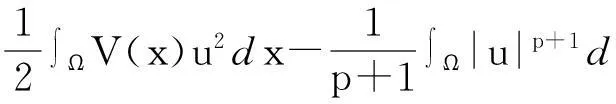
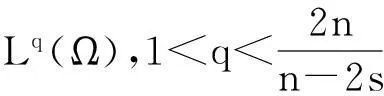
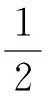
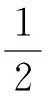
由于p>1，可找到r>0使得：

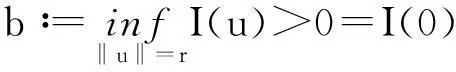
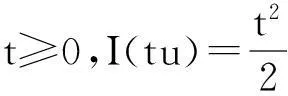
由山路引理[6]可知，I有临界点，从而问题(1)有非平凡解.

参考文献

[1]Dipierro S, Ros-Oton V, Valdinoci E. Nonlocal problems with Neumann boundary conditions[EB/OL]. [2014-07-11]. http://arxiv.org/abs/1407.3313v3.

[2]Nezza Eleonora Di, Palatucci G, Valdinoci E.

Hitchhiker′s guide to fractional Sobolev spaces[J]. Bull Sci Math, 2012,136:521-573.

[3]Lin C S, Ni W M, Takagi I. Large amplitude stationary solutions to a chemotaxis system[J]. J Differential Equations, 1988,72(1):1-27.

[4]Ambrosetti A, Malchiodi A, Ni W M. Singularly perturbed elliptic equations with symmetry: existence of solutions concentrating on spheres I[J]. Comm Math Phys, 2003,235(3):427-466.

[5]Ambrosetti A, Rabinowitz P H. Dual variational methods in critical point theory and applications[J]. J Funct Anal,1973,14:349-381.

[6]Brezis H,Coron J M, Nirenberg L. Free vibrations for a nonlinear wave equation and a theorem of P. Rabinowtiz[J].Comm Pure Appl Math,1980,33:667-689.