在轨服务的超近距离姿轨联合控制研究

郭雯婷，卢 山

（1.上海航天控制技术研究所，上海 201109 2.上海市空间智能控制技术重点实验室，上海 201109）

0 引言

随着航天技术应用领域的飞速发展，航天器的结构和组成日趋复杂，性能与技术不断提高，保证航天器在复杂的空间环境中更持久、稳定、高质量地在轨运行，已成为目前亟待解决的重要问题［1］。利用在轨服务技术可对复杂大型航天器进行在轨组装以及对发生故障失效或燃料耗尽的航天器进行在轨捕获、模块更换、燃料加注等操作，从而可增强航天器的性能，延长航天器的使用寿命，降低费用和风险，在轨服务与操作技术有广泛的应用前景。为实现在轨服务与操作，航天器常需经历远程导引、近程导引、超近程停靠、捕获等阶段，其中超近距离的相对姿态轨道联合控制技术是实现在轨服务的核心，直接关系任务的成败。因此，在轨服务与操作技术研究目标是解决超近距离自主逼近的相对姿态和轨道联合控制技术。

超近距离的相对姿态和轨道联合控制一需要设计相对姿态控制律，使服务航天器对目标航天器进行姿态跟踪，二需要通过设计服务航天器的相对轨道控制律，使服务航天器沿目标航天器的对接端口方向逼近目标航天器。

目前，相对姿态和轨道一体化控制研究多集中于编队卫星的相对位置姿态控制和近距离交会控制。文献［2－4］针对编队飞行卫星，建立了相对位置姿态的耦合动力学模型；文献［5］针对近距离交会卫星的运动同步设计了相对位置的跟踪控制律。但对超近距离逼近的相对姿轨联合控制研究较少。

本文对在轨服务与目标航天器的超近距离姿轨联合控制进行了研究。

1 相对动力学建模

为保证服务航天器在超近距离能对目标航天器特定部位进行跟踪，其姿态控制需对目标部位进行姿态对准，即相对姿态的控制，同时相对位置仍需完成接近、绕飞等操作，因此超近距离的自主逼近和停靠控制存在姿态轨道耦合，涉及12自由度控制，需对姿态、轨道相对动力学进行建模，耦合性分析和控制律设计。

为描述服务航天器相对目标航天器的位置和姿态运动，定义如下坐标系。

a）地心惯性坐标系oi－xiyizi：原点在地心；oixi轴指向春分点；oizi轴与地球自旋轴重合；oiyi轴与oixi、oiyi轴形成正交右手坐标系。

b）航天器第一轨道坐标系：原点在航天器质心；x轴沿径向背离地心；y轴在轨道面内垂直于x轴指向前方；z轴与x、y轴构成右手坐标系。对主动星和目标星，分别有主动星第一轨道坐标系oc－xcyczc和目标星第一轨道坐标系ot－xtytzt。

c）航天器本体坐标系：原点在航天器质心；三轴与本体固连，x轴与体纵轴重合指向前；z轴指向航天器对地面；y轴与x、z轴构成正交右手坐标系。对主动星和目标星，分别有主动星本体坐标系oc－xcbycbzcb和目标星本体坐标系ot－xtbytbztb。

1.1 相对姿态运动动力学建模

航天器绕任意点均有3个转动自由度，需用3个独立变量才能确定航天器在空间的姿态。本文采用相对四元数作为相对姿态的描述参数，目标航天器和服务航天器姿态运动学方程为

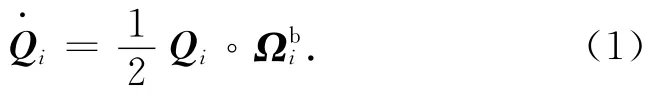
式中：i＝t，c，分别表示目标航天器和服务航天器；Qi为两航天器本体系相对惯性系的姿态四元数；Ωbi分别为两航天器本体系相对惯性系的旋转角速度矢量的矢量四元数在本体系中的表示。定义相对姿态四元数Qr为目标航天器本体系相对服务航天器本体系的姿态四元数，Qt＝Qr◦Qr，则

式中：符号“＊”表示共轭。

两航天器的绝对姿态动力学方程为

式中：ωi为两航天器相对惯性系的旋转角速度在其本体系中的表示；Ii为两航天器的转动惯量在其本体系中的表示；Ti为作用于两航天器的控制力矩；Di为两航天器的外部干扰力矩；符号“×”表示斜对称矩阵。

为使相对姿态与绝对姿态的运动学方程形式一致，定义相对角速度为目标航天器本体相对服务航天器本体的相对旋转角速度在服务航天器本体系中的表示，有

式中：Ccb／tb为由目标航天器本体系至服务航天器本体系的转换矩阵。对式（4）求导并以矩阵形式表示，则有

式中：

则有

进而有

因此，相对姿态动力学方程为：

由式（8）可知：相对姿态运动可通过Tc控制。

1.2 相对轨道动力学建模

在地心惯性坐标系中，两航天器的绝对轨道动力学方程可表示为

式中：ri为两航天器地心距矢量；ui为施加于两航天器的控制加速度矢量；di为两航天器摄动加速度；μ为地球引力常数。

两航天器绝对轨道动力学方程相减，并令rcrt＝rct＝l＋ρ，可得精确的相对轨道动力学方程为

式中：l为目标航天器到控制目标点的位置矢量，可根据最终逼近段的要求与约束条件进行轨迹设计；ρ为控制目标点至服务航天器的相对位置矢量，如图1所示。

图1 相对位置矢量Fig.1 Relative position vector

根据在活动坐标系中矢量导数的规则，将式（10）在目标航天器第一轨道系中投影可得

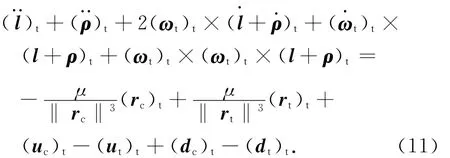
式中：（ωt）t，）t分别为目标航天器轨道坐标系的绝对角速度和角加速度，其在ot－xtytzt系中的投影分别为（1＋etcosθt）2。此处：θt为服务航天器的真近点角，且。其中：pt，et分别为服务航天器半通径和偏心率。将式（11）化为状态变量形式

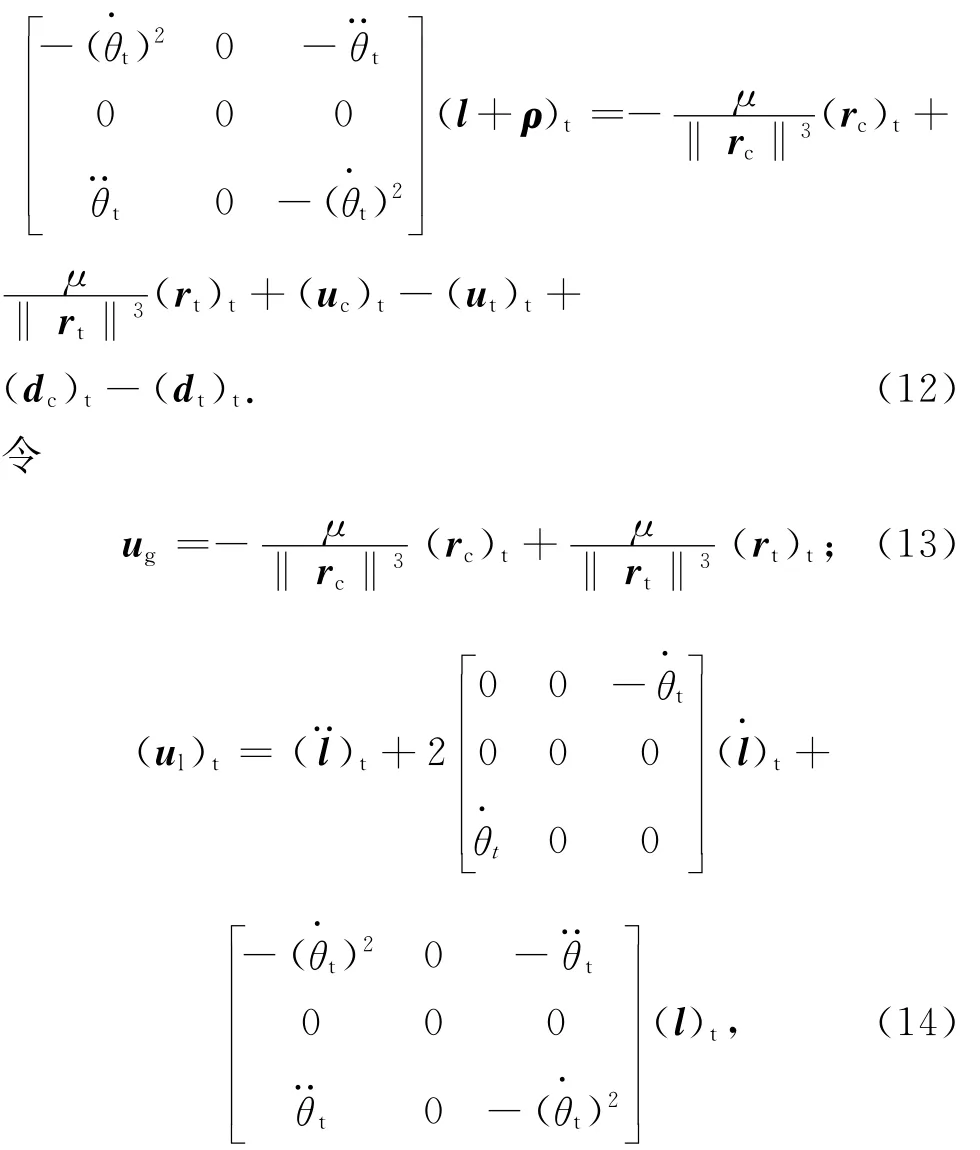
则完整的相对轨道动力学方程为

对服务航天器和目标航天器超近距离的相对运动，ρ为小量，对ug项通过取一阶近似（线性化）进行简化。由ρ＝［xyz］T，（rt）t＝［0 0 －rt］T，（rc）t＝［xyz－rt］T，将ug项改写为分量形式

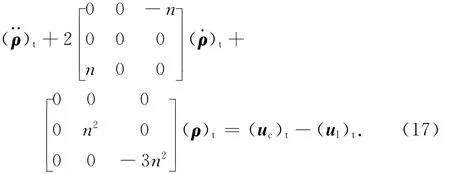
1.3 姿态轨道耦合性分析

服务航天器自主逼近与捕获目标航天器过程中，相对姿态与轨道耦合，主要包括以下耦合。

a）服务航天器推力器沿本体安装，相对轨道动力学建立在目标航天器轨道系中，需将控制加速度转换至服务航天器本体系中，该转换与姿态相关，称为控制输出耦合。其转换矩阵

式中：Ct／i为惯性系至目标航天器轨道系的转换矩阵；Ci／c为服务航天器轨道系至惯性系的转换矩阵；Cc／cb为服务航天器本体系至轨道系的转换矩阵。

b）相对位置和相对速度的跟踪指令（即设计的逼近路径）随目标航天器姿态而变。此耦合是由控制指令产生的，称为控制指令耦合。其转换矩阵

式中：Ccb／tb为服务航天器相对目标航天器的姿态转换矩阵，可由相对测量获得的目标航天器相对服务航天器的姿态转换矩阵求逆得到。

c）需将相对测量获得服务航天器本体系中目标航天器相对服务航天器的位置、速度转换至目标航天器轨道系中进行控制，该转换与服务航天器自身姿态有关，称为控制输入耦合。有

2 超近距离姿轨联合控制设计

超近距离段一般从服务航天器与目标航天器相距300～100m开始，直至两航天器零距离接触，实现对接或抓捕。该阶段具有相对距离近、安全性突出、相对控制精度要求高、控制周期短等特点。近程导引段两飞行器距离相对较远，变轨燃料最少是主要设计因素，超近距离段则主要考虑安全性和控制精度。

在超近距离段，服务航天航天器一般沿视线方向以准直线轨迹逼近目标航天器，根据飞行轨迹安全性，相对导航视场角，以及捕获与对接的技术要求，实施相对状态自主控制［6－7］。相对状态及其变化率由相对导航系统获得。

2.1 相对姿态控制律

设目标航天器相对自身轨道坐标系保持姿态稳定，其控制力矩仅用于稳定自身姿态，为最终平移段的接近创造条件，并不直接参与交会对接相对姿态机动；服务航天器以目标航天器姿态为目标姿态（期望姿态），根据相对姿态四元数和相对旋转角速度进行姿态控制，实现对目标的姿态跟踪［8］。

根据相对姿态动力学方程，设计非线性反馈控制律由非线性反馈项Tc1（用于抵消耦合力矩）和四元数与角速率线性反馈项Tc2两部分组成，即

式中：

此处：KP，KD为反馈增益系数矩阵，且KP＝kpIc；KD＝kdIc。其中：kp，kd为反馈增益系数。将式（21）代入式（8），则有

根据q1，qr的简化，可得

显而易见，此为典型的线性二阶系统方程，根据系统的动态响应要求，选择适当KP，KD便可使控制系统稳定。

2.2 相对轨道控制律

2.2.1 基于LQG的实时闭环反馈轨道控制算法

为实现高精度的相对轨道控制，采用最优实时闭环反馈控制方法，以预先设计的路径作为参考量，确保每个控制周期内航天器都能跟踪预期的相对轨迹。

根据相对轨道动力学方程，选择状态向量

则可写成状态空间形式

式中：u＝Ct／cb（uc）cb－Ct／cb（ul）tb；

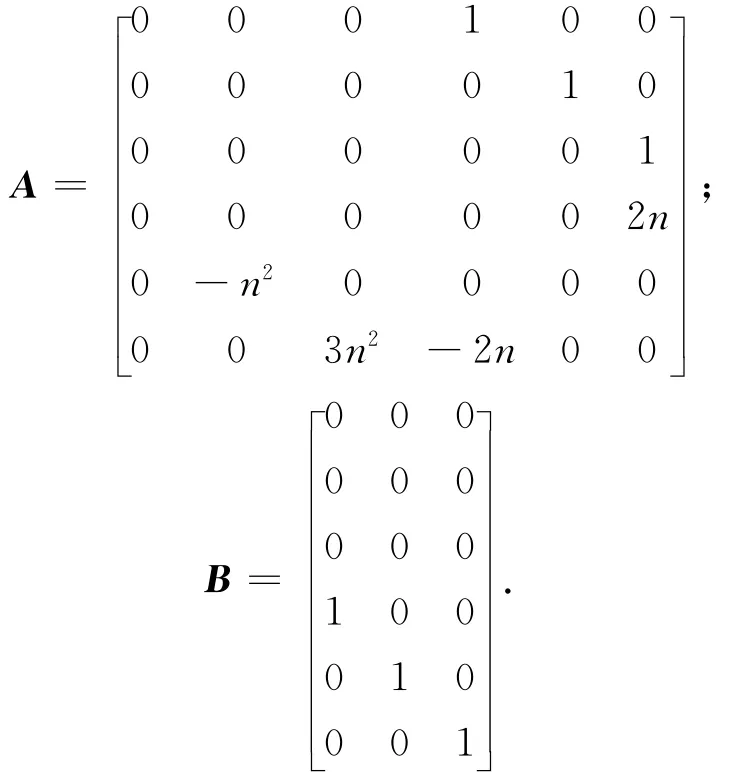
超近距离的相对轨道控制是寻找合适的轨道控制律uc将式（27）中的X控制为0。此为状态调节器问题，可用现代控制理论中的线性二次型调节器（LQR）进行设计［9］。

离散化式（27），得

寻找线性系统式（28）的最优状态反馈控制律uk＝－KXk，使二次型目标函数

达到最小。此处：Q，R分别为状态量和控制量的加权矩阵。

根据极小值原理，可得LQR最优控制律的状态反馈增益矩阵

式中：P为对称非负定矩阵，满足离散Riccati方程

由uk反解出作用在服务航天器本体系上的控制加速度

2.2.2 相对运动轨迹

由自主闭环轨控可知，LQG控制算法使服务航天器在逼近目标航天器时，控制目标点存在一个突变过程，速度量（ul）t及相对状态量发生突变会直接导致控制加速度发生突变，进而易造成控制超调，因此需进行轨迹设计。逼近轨迹设计主要用于接近目标特征部位，为最后在轨操作或对接创造条件。传统的逼近轨迹在相对轨道动力学影响下为曲线，故在逼近过程中会造成视场角变化，不利于相对跟瞄设备持续跟踪目标，在超近距离内可能会造成目标丢失发生碰撞的危险。采用直线逼近方式，给定逼近的时间与目标点，按某种函数规律平滑变化，可设计出一条直线逼近轨迹，在逼近的起始点和终端点满足边值条件，轨迹上每点都可得到期望的相对位置和相对速度，将其输入控制系统进行相对轨迹控制，可使每一时刻服务航天器均在期望的位置，并具期望的相对速度，避免与目标发生碰撞。同时，直线逼近可保证目标始终处于服务航天器的某一方向，利于相对跟瞄设备对目标的稳定跟踪，提高任务的可靠性。

先设计l的y、z分量为

则在目标飞行器轨道坐标系中，控制目标点在y、z向的坐标始终保持为0，服务航天器相对目标的运动轨迹始终保持在x轴附近。

其次合理设计控制目标点l的x分量，使其按某种函数规律平滑变化，同时在逼近的起始点和终端点满足边值条件。x分量的设计可归为一个两个边值条件问题，此两点边值问题有无穷多解。设lx划分为下列4个阶段。

a）加速段，采用等加速度进行加速逼近；

b）等速逼近段，利于服务航天器快速安全地逼近目标航天器；

c）速度衰减段，在短时间内速度衰减到较小的量值，为停靠或对接做准备；

d）慢速靠拢段，在对接前的最后数米，以较小的速度靠拢，利于在轨操作［10－11］。

设计靠拢速度为：在最后靠拢阶段，无论制导机动正常与否，服务航天器与目标航天器的接触速度在安全范围内，不会造成危险。设计的逼近轨迹如图2所示。

图2 逼近轨迹设计Fig.2 Trajectory design for proximity relative motion

将设计的轨迹作为控制系统的参考输入，通过自主闭环反馈控制律对服务航天器轨道状态施加反馈控制，使其始终保持在目标轨道系中的设计点处。因该轨道控制作用为连续状态反馈，故其精度较高。

2.2.3 脉宽调制

因LQG算法获得的轨道控制加速度为连续的，但服务航天器配置的推力器只能提供恒定推力，为此本文采用脉冲调宽算法。脉冲调宽本质是通过控制定常推力发动机在每个控制周期内的工作时间，以保证发动机实际作用冲量与控制律在该控制周期内的所需冲量相等。具体的实现方法为：根据LQG轨道控制算法求出作用于服务航天器的控制力加速度为（uc）cb，则在采样周期内，3个方向上作用于服务航天器的冲量分别为

式中：m为服务航天器质量；ΔT为轨控周期。根据确定的控制加速度，按采样周期内冲量相等原则，3个方向上发动机推力作用时间分别为

式中：Fx，Fy，Fz为三个方向的轨控推力。若发动机能提供的最小脉冲宽度为ΔTmin，采样周期为ΔT，则对tx，ty，tz进行处理

此即为用恒定推力模拟连续轨控加速度的脉冲调宽算法。

3 数学仿真

仿真中航天器初始轨道要素见表1，服务航天器从目标航天器正后方200m接近至目标0.5m。取仿真时间1 000s，仿真步长0.1s，用本文方法所得超近距离段姿态轨道联合控制的仿真结果如图3～7所示。

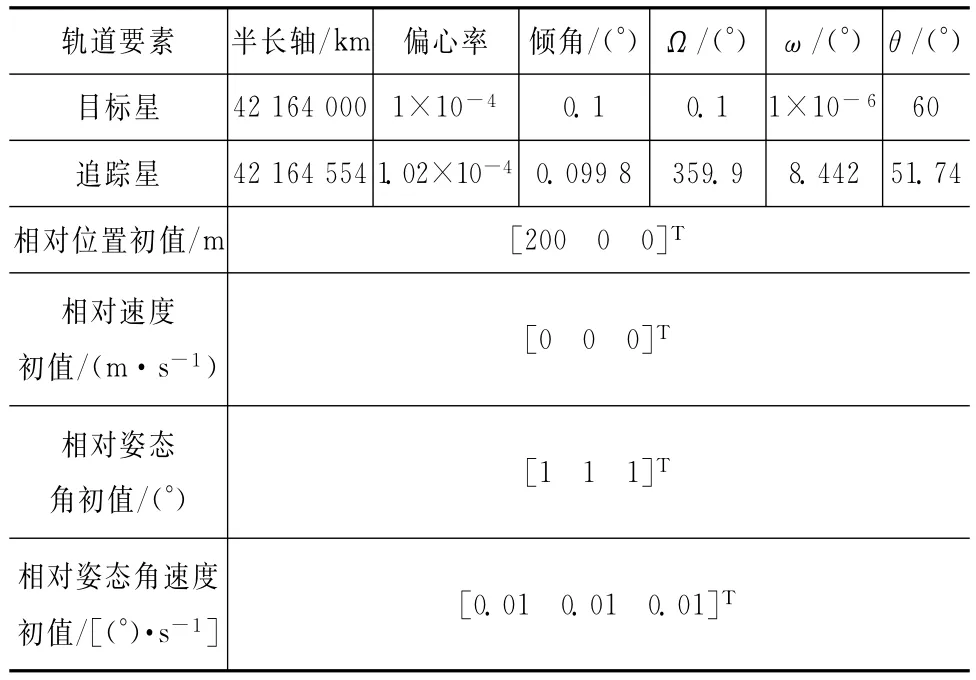
表1 两航天器初始参数Tab.1 Initial elements of two spacecraft

图3 相对位置Fig.3 Relative position

图4 相对速度Fig.4 Relative velocity

图5 相对姿态角控制误差Fig.5 Relative attitude angular position error

由图可知：经约800s服务航天器从目标航天器正后方200m直线逼近至0.5m处，相对位置控制精度优于0.15m，相对速度也逐渐趋于零；目标航天器相对服务航天器的三轴姿态角控制精度优于0.5°，三轴姿态角速度控制精度优于0.02 （°）／s。仿真表明，本文的相对轨道和姿态联合控制算法可行，且控制性能较好，满足高精度交会对接的需求。

图6 相对姿态角速度控制误差Fig.6 Relative attitude angular velocity error

图7 轨道平面内相对运动轨迹Fig.7 Trajectory of relative motion

4 半物理仿真

为进一步验证本文超近距离姿轨联合控制方法的正确性，用地面半物理仿真试验进行验证。超近距离姿轨联合控制试验系统所用的仿真平台由零重力气浮台、目标星模拟器、追踪星模拟器、目标与测量定位系统、地面控制台、动力学宿主机、动力学目标机和视景仿真计算机等组成。其中：气浮平台上的卫星模拟器模拟失重环境中的动力学；仿真计算机根据相对状态量和逼近、悬停的任务规划，解算控制律，并控制追踪星模拟器按指定路径运行；视景仿真系统演示在轨飞行器的运行状态。在与数学仿真参数相同的条件下，半物理仿真结果如图8所示。分析试验数据可知：模拟器的相对位置控制精度最终优于1cm，相对姿态控制精度优于0.1°，满足最终的对接、捕获控制精度的需求。

图8 主动星模拟器相对距离Fig.8 Relative distance

5 结束语

本文对在轨服务的超近距离姿轨联合控制方法进行了研究。建立了两航天器超近距离相对运动中，两航天器基于相对四元数的相对姿态运动动力学方程和基于相对运动轨迹设计的相对轨道动力学模型，根据动力学模型耦合特性，设计非线性相对姿态控制律，并考虑姿态运动的耦合作用，设计了具有姿态信息反馈的较强鲁棒性的控制律，以获得高精度的交会对接控制。数学仿真和半物理仿真结果验证了方法的有效性和可行性。

［1］ 陈小前，袁建平，姚 雯，等.航天器在轨服务技术［M］.北京：中国宇航出版社，2009.

［2］ SEBASTIAN G.Modeling the coupled translational and rotational relative dynamics for formation flying control［R］.AIAA，2005－6091.

［3］ PAH H，KAPILA V.Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics［C］／／Proceedings of the 40thIEEE Conference on Decision and Control.New York：IEEE，2001，3：2057－2062.

［4］ 吴云华，曹喜滨，张世杰.编队卫星相对轨道与姿态一体化耦合控制［J］.南京航空航天大学学报，2010，42（1）：13－20.

［5］ SUBBARAO K，WELSH S.Nonlinear control of motion synchronization for satellite proximity operations［J］.Journal of Guidance，Control，and Dynamics，2008，31（5）：1284－1294.

［6］ PHILIP N K，AANATHASAYANAM M R.Relative position and attitude estimation and control schemes for the final phase of an autonomous docking mission of spacecraft［J］.Acta Astronautica，2003，52（7）：511－522.

［7］ CLAUDINON B，MARCHAL P，FEHSE W.Control techniques for rendezvous and docking：IFAC Automatic Control in Space［C］.Toulouse：1985.

［8］ 朱仁璋.航天器交会对接技术［M］.北京：国防工业出版社，2007.

［9］ 李国勇.最优控制理论及参数优化［M］.北京：国防工业出版社，2006.

［10］ 朱仁璋，尹 艳.论空间交会最终平移段制导设计［J］.中国空间科学技术，2004，24（5）：1－8.

［11］ 朱仁璋，汤 溢，尹 艳.空间交会最终平移轨迹安全模式设计［J］.宇航学报，2004，25（4）：443－448.