基于改进粒子群算法含双馈风电机组配网无功优化研究

奚露露，周玲，杨明耀，徐运兵

（1.江苏省电力公司 检修分公司，江苏 南京 211102；2.河海大学 能源与电气学院，江苏 南京 210098；3.山东省济宁供电公司，山东 济宁 272023；4.常州博瑞电力自动化设备有点公司，江苏 常州 213025）

基于改进粒子群算法含双馈风电机组配网无功优化研究

奚露露1，周玲2，杨明耀3，徐运兵4

（1.江苏省电力公司 检修分公司，江苏 南京 211102；2.河海大学 能源与电气学院，江苏 南京 210098；3.山东省济宁供电公司，山东 济宁 272023；4.常州博瑞电力自动化设备有点公司，江苏 常州 213025）

针对风电机组并网后对配电网无功补偿产生的影响，从双馈风电机组自身的有功、无功输出特性出发，基于场景概率的方法计算风力机组出力情况，以网损最小为目标函数寻求优化求解方法。利用改进粒子群算法来实现系统接入双馈风电机组后的无功优化，在Matlab 2013b软件中构造IEEE33节点模型并利用该算法求解。结果表明，双馈风电机组在参与系统无功优化时具有良好的性能，验证了该改进算法的有效性。

改进粒子群算法；双馈风电机组；无功优化；场景概率；配电网

当今风力发电技术迅速发展，但由于风电自身的随机性和间断性，给并网后的系统造成了一定的影响[1]。传统风力发电机组大多是异步发电机，其在向系统注入功率的同时也会吸收系统大量的无功功率，使得系统无功功率严重缺失，造成系统出现电压越限[2-4]等一系列问题。伴随着电力电子技术的发展，双馈感应风力发电机组由于自带的背靠背变流器，实现无功和有功的解耦控制[5]，使其具有一定无功调节能力。双馈感应风电机组在向系统输出功率的同时给予了系统一定的无功支持。

传统配电网的无功优化由于风力发电机组的接入，使得原先的节点电压、网络损耗等问题的研究环境发生了变化[6-7]，所以，此时要充分考虑双馈感应风力发电机组的连续无功功率支持特性对配电网无功优化带来的影响。

本文首先深入分析了双馈风电机组自身的有功、无功输出特性，充分考虑了其自身在配电网无功优化过程中的支撑作用。然后在寻求最低网损的目标函数约束下，基于改进粒子群算法给予求解，利用IEEE33节点系统进行仿真验算。验证了双馈风电机组在参与无功优化时的无功支撑作用及该改进算法的有效性。

1 双馈感应风电机组模型和功率特性

如图1所示，双馈感应风电机组由桨叶、齿轮箱、双馈感应发电机和背靠背变流器等部分组成[8]。双馈感应风电机组对系统的无功功率支持主要由2部分组成：定子侧和网侧变化器。当双馈机组采取恒功率因素控制方式运行时，双馈机组向系统注入的总无功功率Qtotal等价于定子侧的无功功率Qs：

式中：Qc为网侧变流器向系统中注入的无功功率，当Qc=0时，Qtotal=Qs。

根据双馈感应发电机的T型等效电路，如图2所示。

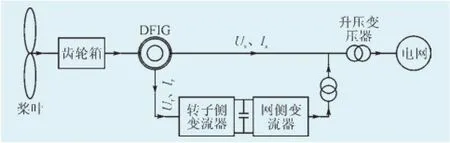
图1 双馈感应风力发电机组Fig.1 Double fed induction wind power generation

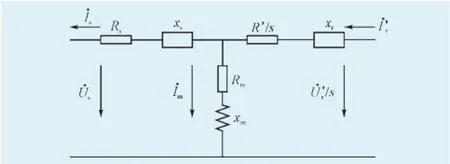
图2 双馈感应电机T型等效图Fig.2 T-equivalent circuit diagram of DFIG

可以得到双馈感应发电机的无功功率极限表达式为：

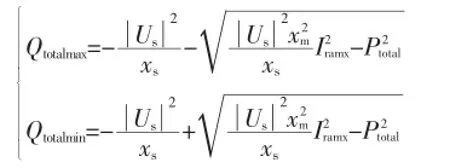
式 中：Qtotalmax和Qtotalmin为 双馈 感应 机组 的无 功功 率最大值和最小值；xs为定子绕组的电抗；Us为定子侧电压；Ptotal为机组输出的有功；Iramx为转子侧变化器电流最大值。当双馈感应电机定子最大电流和转子侧变化器最大电流给定且双馈电机有功功率在额定功率内变化时，相应的无功在一定的区域内进行调节，当 有功 为Ptotal时，无功 的输 出范 围则 为[Qtotalmin，Qtotalmax]。另外，当双馈电机有功越大时，其无功调节的范围则会越小。

2 基于场景概率的决策方法

2.1 基于场景概率的目标评估

目前用的最多的评估目标就是考虑场景发生概率的目标函数期望值[9-11]。表达为：

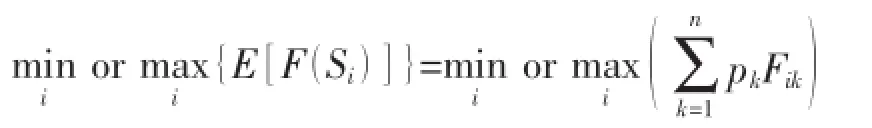
式中：选取的典型场景总数是n；si为可选的规划方案i；Fiκ为在方案Si下，第κ个场景发生时的目标函数值；pκ为第κ个场景下会出现的概率；为规划方案Si在所有可能场景下的目标函数期望值，对于每一个可选的规划方案Si，其期望值与方案Si在n个场景中的目标函数值以及各场景发生的概率有关。

2.2 基于场景概率的风机模型计算

首先采用普遍认同的威布尔双参数曲线方程来作风频分布规律的理论计算，其概率密度方程为：

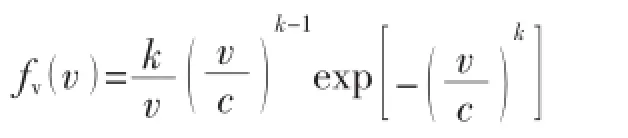
式中：c和κ分别为形状和尺度参数。

本文仅考虑风电机组输出功率的特点进行场景划分，根据风速统计规律计算各典型场景发生的概率，将风机输出功率分为以下3个典型输出。

(1）额定功率输出

(2）停机输出

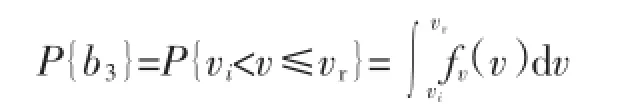
式中：vi为切入风速；vr为额定风速；vc为切出风速。从而进一步可以得到：

(3）欠额定输出

式中：N为风电机组的总场景个数；Ki为第i种场景概率分布值；为第i种场景下的风机网损值。风机出力的不确定性则用对应的场景代替，从而达到全场景下的平均意义上的优化，以各场景发生概率的目标值作为最优评估目标。

3 改进粒子群算法

改进一：本文把惯性权重系数引入到速度进化方程中来改善其收敛性能，并且粒子对当下速度继承的大小与惯性权重系数的大小相关[12-15]。因此，基本PSO算法是惯性权重系数ω=1的特殊情况。该权重系数让粒子产生惯性，增强其光宇搜索和局部搜索能力，因为权重系数可以平衡粒子的探索能力和开发能力，这样当引入后，可以消除基本PSO算法对粒子最大飞行速度vmax的依赖，ω的大小意味着粒子惯性的大小，从而决定粒子在原有方向保持速度的大小。从这个意义上看，调节惯性权重系数ω可以将固定设定在变化范围内。一般粒子群在初始飞行时，如果能够具有好的探索能力，这种情况是希望被看到的，就是说在粒子飞行的末期，当迭代次数增加时，对于粒子的开发能力也要求较高。所以动态调节惯性权重就显得很有必要。设最大迭代次数κmax，并且惯性权重系数的取值范围为则第i次迭代时可表示为：

改进二：从局部版PSO算法的全局性能好的特点受到启发[16-18]，将基本PSO算法中的粒子状态个体极值由所有粒子的个体极值的平均值来代替，这样可以更有效地避免算法陷入局部极值，减小个别极优粒子的个体效应，增加粒子群的群体性，宜于跳出局部极值。经过改进后粒子速度和位置的更新方程式为：

式中：c1和c2为加速系数；N1和N2为[0-1]之间的相互独立的随机数，第i个粒子的位位置由xi=（xil，xi2，…，xid）来表示；第i个粒子的速度由vi=（vil，vi2，…，vid）来表示；第i个粒子经历过的历史最好位置可以用pi=（pil，pi2，…，pid）来表达；群体内所有粒子经过的最好的位置可以用pg=（pgl，pg2，…，pgd）来表达。

基于改进PSO的算法流程：

1）给每个粒子一个随机的初始位置和初始速度。

2）根据适应度函数计算每个粒子适应度。

3）比较每一个粒子自身的适应度值与其经历过的最优位置的适应度值，取最优者作为更新个体的最优值，并用目前的最优值更新新个体的历史最优值；若没有更好的，则取粒子经历过的最优点。

4）让每个粒子的历史最优值与群体内或邻域所经历的最好解的适应度值进行大小比较，取最优者作为目前全局最好解。

5）将粒子位置和速度更新。

6）判断是否满足结束条件，若没有，转至2）。

4 优化模型

无功优化的主体思想是满足系统的各种约束情况下，改变变压器分接头，发电机机端电压，并联电容器的容量这几个控制变量，从而使系统的网损最小、电压水平合格，达到经济运行的目的。本文考虑了双馈机组并网后对电网的影响，将双馈风力发电机组的无功出力考虑到系统的无功优化中，用最小方式运行来求解运行规划的问题。

4.1 目标函数

4.1.1 最小负荷方式和一般负荷方式

在最小方式和一般方式下，此时所采用的无功优化的原则是：在满足各种约束条件下使得系统的网损最小。目标函数为：

4.1.2 电压稳定性指标

指标方程表达式：

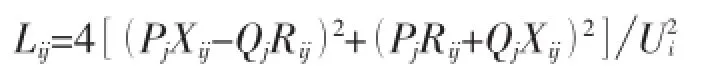
式中：Qj、Pj为节点j处的流入无功功率和有功功功率；Rij和Xij为支路的电阻和电抗；Ui为节点电压。则整个电网的电压稳定性指标[19]为：

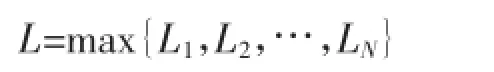
L代表电网的电压稳定性情况，它的值是远远小于1的，并且L越小反应电网电压稳定性情况越好。

4.2 约束条件

4.2.1 等式约束方程

式中：PGi、PFi、PLi分别为节点i发电机注入的用功功率、风电机组注入的有功功率、负荷吸收的有功功率；QGi、QFi、QCi、QLi分别为节点i发电机注入的无功功率、风电机组注入的无功功率、电容器组注入的无功功率、负荷吸收的无功功率；Ui为i点的电压；Gij为节点i、j之间的电导；Bij为节点i、j之间的电纳；θij为节点i、j之间的相角差。

4.2.2 不等式约束方程

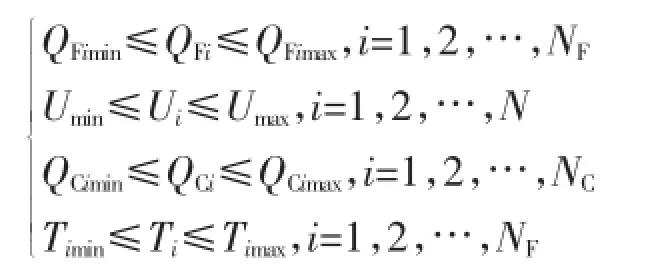
式中 ：QFimax、QFimin为风机 无功 出力 的 上下 限 ；Umin、Umax分别为节点电压幅值的下限值和上限值 ；QCimax、QCimin为第i个并联电容器组投入的无功容量；Timax、Timin第i个可调变压器抽头位置上下限，并且NF、NC、NT分别为风机个数、需要补偿的节点总数、有载调压变压器的个数。

综上可知，在最小负荷运行方式时，通过以全网网损最小作为目标函数来进行优化，可以求得补偿点的单组容量。

5 算例仿真

为了进一步讨论双馈感应风电机组作为无功源参与系统无功优化的优势以及特性，本文采用IEEE33节点系统进行系统仿真研究，系统的网络结构如图3所示，节点参数见参考文献[20]，节点0是平衡节点，电压幅值为10.5 kV，相角为0，取基准功率为1 000 kV·A。节点7、11、14、28为补偿节点，每个节点有5组电容器，单组容量为50 kvar。

图3 IEEE33节点系统图Fig.3 IEEE33 System

有载调压变压器分接头开关拥有9个档，调节范围从0.95～1.05 pu之间，并且在节点17和32节点分别有一台1 500 kW的变速恒频双馈感应风电机组。风电机组的机端的额定电压为690 V，风速的分布Weibull模型中c和κ的取值分别为9.19和1.93，切入风速、额定风速、切出风速分别为4 m/s、12 m/s、25 m/s。场景1（停机状态）、场景2、（欠额定状态）、场景3（额定状态）发生的概率分布为0.111、0.704、0.188并且可计算出场景的输出的平均有功功率分别为：0 MW、0.284 MW、1.5 MW，从而可以得到双馈风电机组的有功概率输出期望为0.48 MW，并且此时的无功功率极限为（-3.55，0.624）。在PSO算法中，粒子数N= 50；最大迭代次数为100，权重系数在[0.4，0.9]之间线性递减，并且初值取0.8；加速系数c1、c2取2.0。

表1 系统有无双馈风电机组对比情况Tab.1 Comparison of results based on system with DFIG/without DFIG

在系统中加入风电机组，考虑风电机组的无功出力后，和没有加入风电场相比，网损由原来的142.13 kW下降到123.96 kW，在原来的基础上下降了12.78%，优化过后系统的节点电压也得到了改善。这是由于风速较高、风电机组输出有功功率较大的时候，会从系统吸收无功功率以降低系统节点电压，维持系统节点电压不会过高，在允许的范围内变化；而当风速较低、风电机组输出有功功率较少时，会向系统发出无功功率以支撑系统节点电压，以维持此时节点电压不会低于规定值。并且对比发现无功优化以后可以有效减小网损，提高系统的电压水平。

综合场景最小方式运行下，使用改进粒子群算法比基本粒子群算法在抬升系统各节点电压、改善电压质量方面有着显著优点，如图4所示。并且所有的节点电压都在允许范围之内，符合条件。

6 结论

运用场景概率模型能更好地体现风电场的功率特性，双馈感应风电机组作为无功源参与系统的无功优化，通过双馈风电机组自身的无功调节能力，对系统的运行状态有很大的改善，可以起到较好的调节电压，降低网损的作用。通过算例仿真，改进粒子群算法具有良好的效果，收敛性不错。

图4 各系统节点电压对比图Fig.4 Comparison curve of voltage at each point

[1]张志春，刘洪伟.我国发展风电产业的战略性分析[J].电网与清洁能源，2013，29（5）：67-72. ZHANG Zhichun，LIU Hongwei.Strategic analysis of wind power industry development in China[J].Power System and clean Energy，2013，29（5）：67-72（in Chinese）.

[2]孙涛，王伟胜，戴慧珠，等.风力发电引起的电压波动和闪变[J].电网技术，2003，27（12）：62-66. SUN Tao，WANG Weisheng，DAI Huizhu，et al.Voltage fluctuction and flicker caused by wind power generation[J]. Power and Technology，2003，27（12）：62-66（in Chinese）.

[3]余洋，陈盈今，刘立卿，等.大规模风电接入对电网电压稳定性影响的研究[J].电力科学与工程，2010，26（4）：1-4. YU Yang，CHEN Yingjin，LIU Liqing，et al.Study on effect of voltage stability about 1arge scale interconnected wind farm[J].electric Power Science and Engineering，2010，26（4）：1-4（in Chinese）.

[4]张乐丰，王增平.风电并网对电力系统的影响[J].江苏电机工程，2011，30（2）：81-84. ZHANG Lefeng，WANG Zengping.Influences of wind power integration on power system[J].Jiangsu electrical Engineering，2011，30（2）：81-84（in Chinese）.

[5]张会参.双馈风力发电机模型仿真与并网运行研究[D].成都：西南交通大学，2012.

[6]胡传煜.风电发展对我国电网运行可能造成的影响[J].电力与能源，2011，32（3）：213-216. HU Chuanyu.Briefly analysis impact of development of wind power for power grid[J].Power and Energy，2011，32（3）：213-216（in Chinese）.

[7]吴俊，李建设，周剑，等.风力发电并网对电网的影响[J].南方电网技术，2010，4（5）：48-52. WU Jun，LI Jianshe，ZHOU Jian，et al.Influence of wind power generation integration into power grids[J].Southern Power System Technolocy，2010，4（5）：48-52（in Chinese）.

[8]王兴武，张照彦，武永利.变速恒频双馈异步风力发电机建模与仿真研究[J].计算机仿真，2009，26（10）：294-297. WANG Xingwu，ZHANG Zhaoyan，WU Yongli.Modeling and simulation of variable speed constant frenquency doubly fed wind generator[J].Computer Simulation，2009，26（10）：294-297（in Chinese）.

[9]袁越，吴博文，李振杰，等.基于多场景概率的含大型风电场的输电网柔性规划[J].电力自动化设备，2009，29（10）：8-12. YUAN Yue，WU Bowen，LI Zhenjie，et al.flexible planning of transmission system with 1arge wind farm based on multi-scenario probability[J].electric Power Automatic Equipment，2009，29（10）：8-12（in Chinese）.

[10]刘苏云，王笛，蒋丹，等.基于场景概率的风电机组的选址和定容[J].电气自动化，2014，36（5）：38-40. LIU Suyun，WANG Di，JIANG Dan，et al.Scenario probability-based siting and sizing of wind turbine generators[J].electrical Automation，2014，36（5）：38-40（in Chinese）.

[11]雷宇，杨明，韩学山.基于场景分析的含风电系统机组组合的两阶段随机优化[J].电力系统保护与控制，2012，40（23）：58-67. LEI Yu，YANG Ming，HAN Xueshan.A two-stage stochastic optimization of unit commitment considering wind power based on scenario analysis[J].Power System Protection and Control，2012，40（23）：58-67（in Chinese）.

[12]姜志鹏，文习山.粒子群算法应用于避雷器均压环配置优化[J].高压电器，2014，50（1）：102-106. JIANG Zhipeng，WEN Xishan.Application of particle swarm optimization algorithm to configuration optimization of grading rings for arrester[J].High Voltage Apparatus，2014，50（1）：102-106（in Chinese）.

[13]汪兴旺，邱晓燕.基于改进粒子群算法的配电网分布式电源规划[J].电力系统保护与控制，2009，37（14）：16-20，40. WANG Xingwang，QIU Xiaoyan.Distributed generation planning in distribution system based on modified particle swarm optimization algorithm[J].Power System Protection and Control，2009，37（14）：16-20，40（in Chinese）.

[14]孟庆霖.基于蚁群和粒子群算法的风电功率预测策略[D].天津：天津大学，2009.

[15]雷敏，杨万里，彭晓波，等.基于改进粒子群算法的含DG的配电网无功优化[J].华北电力大学学报，2015，42（1）：39-44. LEI Min，YANG Wanli，PENG Xiaobo，et al.Reactive power optimization of distribution network with distributed generation based on improved simple PSO algorithm[J]. Journal of North China electrical Power University，2015，42（1）：39-44（in Chinese）.

[16]华敏.PSO算法在电力系统中无功优化中的应用[D].长沙：湖南大学，2007.

[17]骆君.含风电机组的配电网无功优化研究[D].长沙：湖南大学，2009.

[18]宋景博，潘文霞，普珍，等.考虑接触电压的风电机组接地网优化设计[J].电磁避雷器，2013，32（6）：56-60. SONG Jingbo，PAN Wenxia，PU Zhen，et al.Optimization design of wind turbine grounding grid considering touch voltage[J].Insulators and Surge Arresters，2013，32（6）：56-60（in Chinese）.

[19]周晖，周任军，谈顺涛，等.用于无功电压综合控制的改进粒子群优化算法[J].电网技术，2004，28（13）：45-49. ZHOU Hui，ZHOU Renjun，TAN Shuntao，et al.Application of improved particle swarm optimization to integrated control of voltage and reactive power[J].Power System Technology，2004，28（13）：45-49（in Chinese）.

[20]刘健，毕鹏翔，董海涛，等.复杂配电网简化分析与优化[M].北京：中国电力出版社，2002：36-57.

（编辑 董小兵）

Research on Reactive Power 0ptimization for Distribution Network with DFIG Based on Enhanced PS0 Algorithm

XI Lulu1，ZHOU Ling2，YANG Mingyao3，XU Yunbing4
（1.State Grid Jiangsu electric Power Maintenance Branch Company，Nanjing 211102，Jiangsu，China；2.College of electric and Energy，Hohai University，Nanjing 210098，Jiangsu，China；3.State Grid Jining Supply Power Company，Jining 272023，Shandong，China；4.Changzhou Bori electric Power Automation Equipment Co.，Ltd.，Changzhou 213025，Jiangsu，China）

With focus on the influence of wind power integration on the distribution network reactive power compensation，this paper analyzes the active power and reactive power characteristics of the doubly-fed induction generator（DFIG），and then it calculates the wind turbine output based on the method of scene probability and seeks the optimization method on the objective function of the minimum 1oss of active power. The enhanced particle swarm optimization algorithm is used to optimize the reactive power of the power system with connection of the DFIG and the IEEE 33-nodes model is established in the Matlab 2013b to acquire the optimal solution with this algorithm.The result indicates that DFIG has a good performance in the reactive power optimization for system and thus has verified validity of this enhanced algorithm.

2015-04-09。

奚露露（1989），男，硕士，主要研究方向为可再生能源发电技术；

周 玲（1964），女，副教授，硕士生导师，主要研究方向为电力系统运行与控制；

杨明耀（1990），男，硕士，主要研究方向为电力系统运行与控制；

徐运兵（1989），男，工程师，从事电力自动化设备设计。

1674-3814（2015）08-0094-06

TM761；TM614

A

KEY W0RDS：enhanced PSO algorithm；DFIG；reactive power optimization；scene probability；distribution network