基于模糊可靠度的 SRC 框架结构优化设计研究

第一作者郑山锁男，教授，博士生导师，1960年生

邮箱：zhengshansuo@263.net

基于模糊可靠度的SRC框架结构优化设计研究

郑山锁，王晓飞，何伟，王帆(西安建筑科技大学土木工程学院，西安710055)

摘要：基于“投资-效益”准则，建立SRC框架结构的优化数学模型，优化目标包括初始造价及结构失效损失期望最小化两部分。利用加权系数调整两者重要程度。为获得结构失效损失期望值计算结构失效概率；为获得接近实际的失效概率，对SRC框架结构进行模糊可靠度分析，主要内容包括：确定SRC框架结构抗震目标性能水平量化值，建立结构模糊功能函数，提出考虑模糊性Monte Carlo法。将SRC框架结构优化过程调整为含内外两层的迭代过程，外层对优化模型进行计算，内层对结构进行模糊可靠度分析。考虑优化模型中设计变量、约束条件过多、目标函数非线性程度较高等特点，提出适用于SRC框架结构的分阶段优化计算方法。通过对一榀单跨三层SRC框架结构优化设计，表明所提优化方法可获得理想、可靠的设计效果。

关键词：SRC框架；优化设计；模糊数学；可靠度；分阶段优化

基金项目：国家科技支撑计划(2013BAJ08B03)；国家自然科学基金(51108376，50978218)；高等学校博士学科点专项科研基金(20106120110003)；陕西省科研项目(2012K12-03-01，2011KTCQ03-05)

收稿日期：2014-03-10修改稿收到日期：2014-05-06

中图分类号:TU398+2; O159文献标志码：A

Optimization design for SRC frame structures based on fuzzy reliability

ZHENGShan-suo,WANGXiao-fei,HEWei,WANGFan(School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Abstract:Based on “investment-benefit” rule, the optimization mathematical model of SRC frame structures was established. Optimization objectives included the initial cost minimization and the structural failure loss minimization, and the weighed coefficient was used to adjust the importance of the both. In order to obtain the structural loss expectation, firstly, the failure probability of structures was calculated. In order to obtain the failure probability more close to reality, the fuzzy reliability analysis of SRC frame structures was performed. The main contents of fuzzy reliability analysis included determining the aseismic performance level quantification value of SRC frame structures, establishing structural fuzzy function, and presenting Monte Carlo method considering the fuzziness. The SRC frame structure optimization process was adjusted to a two-level iteration process with the outer layer for optimization design and the inner layer for the structural reliability analysis. Aiming at too many design variables and constraint conditions and the higher nonlinear level of constraint conditions and objective function, the phase-in optimization calculation method for SRC frame structures was put forward. Finally, the optimization design of a one-bay-three-story SRC frame is implemented. The optimization results showed that the optimization method proposed here can obtain ideal and reliable design results.

Key words:SRC frame; optimization design; fuzzy mathematics; reliability; phase-in optimization

地震灾害造成的巨大经济损失使人认识到结构抗震设计只注重安全远远不够，须对结构性能、安全及社会效益等全面考虑。为此，提出基于“投资-效益”准则的结构抗震优化设计理论[1-2]。

该准则中需分析的结构全寿命费用由初始造价与风险损失两部分构成。影响结构风险因素本身具有较大不确定性，如地震荷载、构件材料性能、截面几何尺寸、结构计算分析模型等，欲获得可靠的风险分析应考虑该不确定性，因此，结构优化设计必须以可靠度理论为基础。

传统可靠度理论用极限状态描述结构可靠与否的界限时，由结构可靠状态直接跳跃到失效状态，此绝对的、一刀切的刚性失效准则既不科学也不符合工程实际，因实际结构由可靠到失效为渐进过程，两者之间存在模糊过渡状态。SRC组合结构具有承载能力高、抗震性能好、综合经济效益高等优点，虽已被成功应用于诸多实际工程，但对此类结构基于可靠度的优化研究相对较少，在结构可靠度分析中考虑模糊失效准则的优化研究更寥寥无几。

鉴于此，本文尝试将模糊理论与可靠性理论相结合，用于SRC框架结构可靠度分析，为基于“投资-效益”准则的SRC框架结构优化设计提供理论基础。并针对SRC框架结构特点，参考国内外关于优化方法研究成果，实现SRC框架结构实例优化。

1SRC框架结构模糊可靠度分析

1.1SRC框架结构抗震目标性能水平

SRC框架结构作为新型结构对其研究较少，而我国现行的抗震规范亦未给出性能指标的量化值。本文用层间变形准则作为SRC框架结构破坏准则。分析总结SRC框架柱试验数据[3]，获得框架结构层间位移角限值，见表1。

表1　SRC框架结构的抗震目标性能水平量化值

1.2基于性能的结构模糊功能函数

传统可靠度理论用结构极限状态描述结构可靠与失效界限时，结构从可靠到失效为突然发生，而实际上为渐变过程，在可靠与失效间有一模糊状态。

将结构的模糊随机功能函数记为

(1)

(2)

式中：z为功能函数值；r1，r2分别为过渡区间上、下界限，即容差，用工程中常用的扩增系数法计算，该方法在充分考虑常规设计所累积的经验基础上，通过引入扩增系数λ确定过渡区间容差，一般取(0.05～0.4)倍的许用值[4-5]，即用λ乘以SRC框架结构“不坏、可修、不倒”性能状态下对应的层间位移角标准值，可得对应于不同性能状态的模糊隶属函数容差。

1.3考虑模糊性的 Monte Carlo法

(3)

由于概率密度函数及隶属度函数较复杂，通过直接积分的解析方法求解较困难，本文采用Monte Carlo法进行求解。失效概率可表示为

(4)

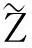
通过引入模糊隶属度函数，将Monte Carlo法中应用确定性失效准则进行判断的示性函数改造为应用模糊失效准则判断的示性函数，即

(5)

1.4SRC框架结构模糊可靠度简化计算方法

计算SRC框架结构可靠度时所用功能函数为

f(u0,X,P)=u0-u(X,P)

(6)

式中：u0为SRC框架结构层间变形能力的随机变量，标准值为SRC框架结构性能水平量化值(表1)；X为与结构本身特性有关的随机变量向量(如结构构件尺寸、材料特性等)；P为荷载作用随机变量向量；u(X,P)为荷载作用引起的结构层间变形随机变量，可由有限元分析获得。

SRC框架结构可靠度计算中的功能函数是设计变量的高度非线性隐函数，若用该功能函数直接计算可靠度，计算量大且不易收敛。故本文对SRC框架结构的可靠度简化处理，将对应于各性能水平的功能函数变为显式形式，则此时功能函数变化为

f(u0,up)=u0-up

(7)

式中：up为地震作用效应随机变量的显式形式。

经简化后，只要知道层间变形分别作为抗力项u0及地震作用up效应项的随机变量标准值及概率统计特征，便可进行结构的模糊可靠度计算。主要步骤为：①确定结构抗力项及地震作用效应项的概率统计特征，包括分布类型、均值与标准值比值及变异系数。②计算SRC框架结构地震作用效应标准值，利用步骤①结果获得地震作用效应平均值；SRC框架结构抗力项标准值(表1)，利用步骤①结果获得抗力项平均值。③在获得抗力项及地震作用效应项概率分布类型、平均值、变异系数后，建立式(7)显式功能函数，之后便可利用改进Monte Carlo模拟法计算结构在不同性能水平下的模糊可靠度。

2SRC框架结构抗震优化数学模型

基于“投资-效益”准则，采用线性加权法构造目标函数，通过调整加权系数改变两个优化目标(初始造价、结构失效损失期望)在目标函数中的重要程度，建立SRC框架结构抗震优化数学模型。

待求设计变量为

X={x1,x2,…,xn}T，X⊂R

(8)

目标函数为

(9)

优化约束条件为

(10)

gj(X)=0，(j=1，2，…，p)

(11)

hk(X)≤0,(k=12…q)

(12)

3SRC框架结构优化设计

基于模糊可靠度的优化设计迭代过程包含内外两层，外层对优化模型进行优化计算，内层对结构进行模糊可靠度分析，流程见图1。

图1　SRC框架结构优化设计方法流程图 Fig.1 The flow chart about optimization design method of SRC frame structure

为简化优化过程，对SRC框架结构优化前，先采用规范方法设计，获得较合理的设计结果，并将该结果中梁、柱构件的混凝土强度等级、纵向受力钢筋、梁侧构造钢筋、箍筋作为优化模型常量，将梁柱截面尺寸、型钢截面尺寸作为优化设计迭代过程初始值。无论规范设计或优化设计，梁、柱构件截面中全部采用对称充满型实腹型钢—焊接工字钢。

SRC框架结构优化模型设计变量为

(13)

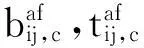
3.1分阶段优化设计方法

考虑优化模型设计变量及约束条件较多、约束条件及目标函数非线性程度较高等特点，参考针对钢筋混凝土的两阶段优化思路[6]，将SRC框架结构优化过程分为两阶段处理。

3.1.1小震时第一阶段优化

(1)设计变量

小震时SRC框架结构优化目标包括初始造价、结构相应于“基本完好”性能失效时的损失期望，约束条件含结构的承载能力约束，则第一阶段优化设计变量为

(14)

(2)优化目标

第一阶段优化目标为

(15)

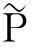
SRC框架结构初始造价表达式为

C0(X)=CostC+CostA+CostS

(16)

(17)

(18)

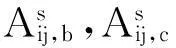
进行第一阶段优化时，将梁、柱构件截面尺寸及型钢截面面积作为设计变量，并将型钢规格表提前存入程序，据型钢截面面积可快速搜索到型钢截面惯性矩Ia，利用设计变量计算获得钢筋混凝土部分惯性矩Ic及截面面积Ac。型钢混凝土构件抗弯、剪刚度为

EI=EcIc+EaIa，EA=EcAc+EaAa

(19)

式中：EI，EA分别为SRC构件截面抗弯及轴向刚度；EcIc，EcAc分别为SRC部分截面抗弯及轴向刚度；EaIa，EaAa分别为型钢部分截面抗弯及轴向刚度。

由此可得建立SRC框架结构层间及杆件模型所需质量、刚度矩阵，进而对框架结构进行动力分析及内力、变形、模糊可靠度计算。

(3)约束条件

承载力约束要求[8,11]。柱抗压承载力约束为

(20)

式中：N，Nu分别为框架柱轴向力设计值及轴向抗压承载力。

柱、梁的抗弯承载能力约束为

(21)

式中：M，Mu分别为框架柱或框架梁弯矩设计值、抗弯承载力。

柱、梁抗剪承载力约束为

(22)

式中：V，Vu分别为框架柱或框架梁剪力设计值、抗剪承载力。

构造要求为

梁尺寸要求：hij,b≥250 mm，hij,b≤4bij,b

柱尺寸要求：bij,c≥350 mm，hij,c≥350 mm

对高跨比大于2.5的梁、剪跨比大于2的柱μV=0.2，其它情况μV=0.15。

柱轴压比要求：

混凝土保护层厚度要求：c≥20 mm

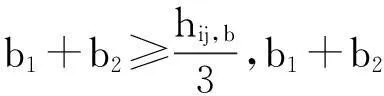
柱中型钢的混凝土保护层厚度：cc≥120 mm。

小震下性能要求为Δsi≤[Δs]，Δsi为按设计变量标准值计算所得SRC框架结构各层间位移角标准值，[Δs]为SRC框架结构层间位移角限值(表1)。

“强柱弱梁”概念设计要求为

3.1.2中震、大震时第二阶段优化

(1)设计变量

第二阶段优化为在获得梁柱构件尺寸、型钢截面面积基础上关于型钢截面尺寸的详细优化。该阶段设计变量为

(2)优化目标

第一阶段优化中，已确定SRC框架结构初始造价与“基本完好”性能下失效损失期望，则第二阶段优化目标为结构在“中等破坏”性能与“严重破坏”性能下失效损失期望之和。此时目标函数为

(24)

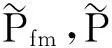
(3)约束条件

由于在中震、大震作用下结构会进入弹塑性状态，故第二阶段优化不存在承载力约束要求，而概念设计要求无需考虑。

构造要求为

框架梁中型钢尺寸要求：

框架柱中型钢尺寸要求：

框架梁、柱中型钢钢板宽厚比要求见文献[8]。

SRC框架柱延性约束

良好的延性能避免脆性破坏发生并进行内力重分布，要使构件具有足够的延性，则延性系数μij,c需满足

式中：

lcor=2(hij,c-2c)+(bij,c-2c)；hcor=hij,c-2c

文中未解释的字母含义见规范[7～10]。

3.2算例

3.2.1工程概况

3层SRC框架结构，见图2。8度(0.2 g)抗震设防乙类建筑，场地为第一组Ⅱ类。据规范[6-9]设计，获得框架梁、柱截面配筋见图3～图6。其中优化初始设计参数为：混凝土强度等级C35；型钢采用Q235。为方便总费用计算，本文按市场价将材料单价调整为：混凝土1×10-3元/mm3；型钢2.886×10-2元/mm3；纵向钢筋2.340×10-2元/mm3；箍筋2.106×10-2元/mm3。

图2　SRC框架立面图(单位：mm) Fig.2 The elevation drawing of SRC frame (Unit: mm)

图3　底层SRC框架梁截面配筋图 Fig.3 Reinforcement figures of SRC frameunderlying beam section

图4　二层SRC框架梁截面配筋图 Fig.4 Reinforcement figures of SRC frame two-story beam section

图5　顶层SRC框架梁截面配筋图 Fig.5 Reinforcement figures of SRC frame top story beam section

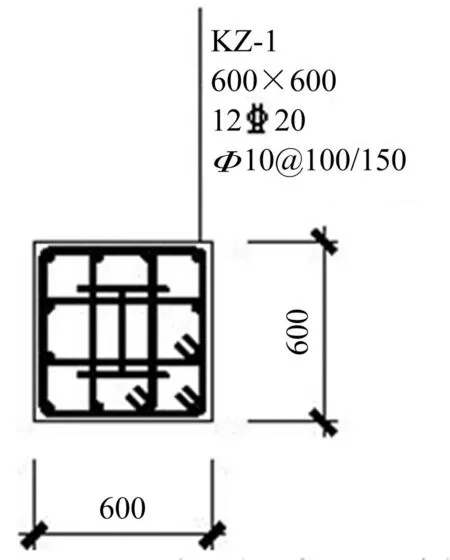
图6　SRC框架柱配筋图 Fig.6 Reinforcement figure of SRC frame column section

图7　目标可靠度指标与加权系数α 1之关系 Fig.7 The relationship between target reliability index andweighted coefficient α 1

采用MATLAB语言将SRC框架结构(图1)优化设计方法编制计算程序对其(图2)进行优化分析，程序主要包括：①地震反应有限元分析；②SRC框架结构层间变形概率分布类型检验；③结构模糊可靠度计算(在结构模糊可靠度计算中，以层间变形为SRC框架结构破坏准则)；④结构离散变量优化计算[12-13]。

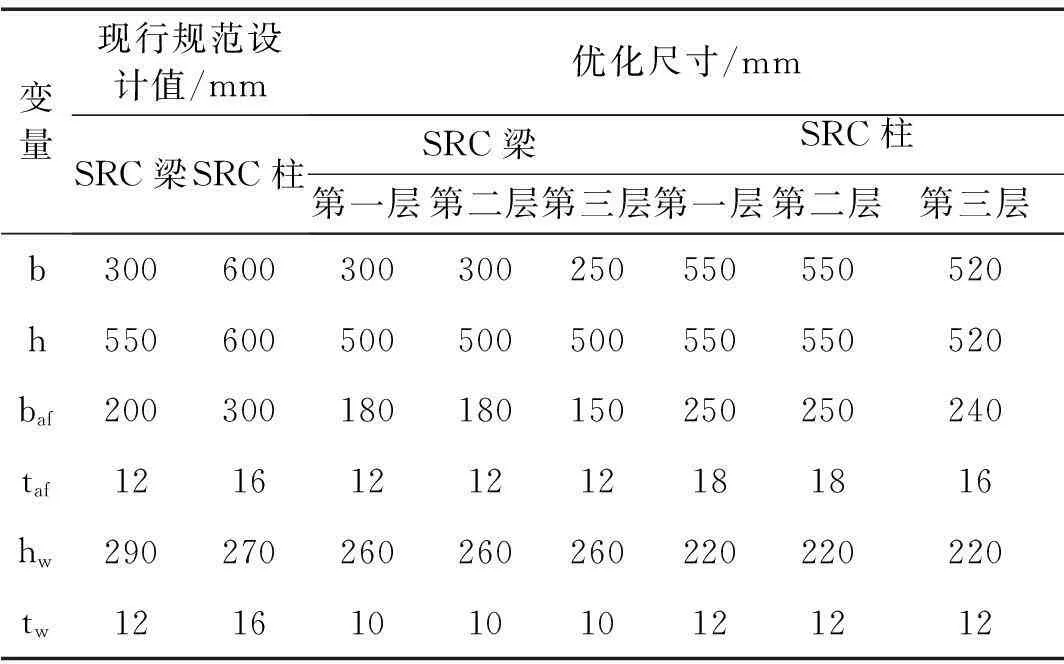
有限元分析程序、层间变形概率分布检验程序及可靠度计算程序为嵌套在优化计算程序中，实际运行时通过优化的m文件分别进行调用，一起组成SRC框架结构的优化设计程序。用该程序对图2框架进行优化，结果见图7、图8。由图7看出，随权重系数α1增加,优化所得结构可靠度指标不断下降，即结构可靠性降低，失效损失增大，与实际情况相符合。当α1取值[0.6～0.4]时，结构可靠度指标较稳定，故本文取α1=0.4,α2=0.6，优化后SRC框架梁、框架柱截面尺寸及内部型钢截面尺寸见表2。

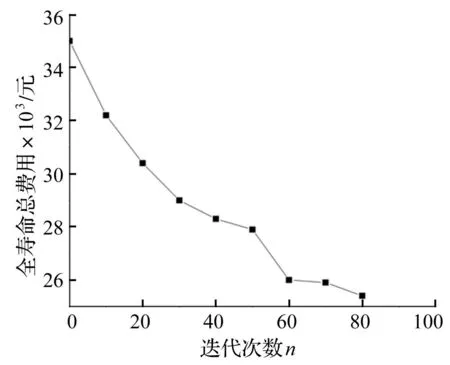
图8　α 1=0.4,α 2=0.6时总费用与优化迭代次数关系 Fig.8 When α 1=0.4,α 2=0.6, the relationship between total cost and optimal iteration numbers

变量现行规范设计值/mm优化尺寸/mmSRC梁SRC柱SRC梁SRC柱第一层第二层第三层第一层第二层第三层b300600300300250550550520p50600500500500550550520baf200300180180150250250240taf1216121212181816hw290270260260260220220220tw1216101010121212

注：表中变量b，h分别为构件截面宽度及高度；baf，taf，hw，tw分别为型钢翼缘宽度及厚度、腹板高度及厚度。

表3　α 1=0.4,α 2=0.6时优化前后造价对比

分析图8、表3知，结构全寿命总费用经优化后下降27.4%，初始造价优化后下降30.8%，但结构失效损失期望经优化后仅由初始造价的31.6%增加到38%，可见采用本文所提优化方法，既能获得较好的经济效益，亦能一定程度上保障结构性能，使结构设计在经济性与平衡性之间取得最佳。

4结论

(1)对文献[2]的基于“投资-效益”准则框架结构抗震优化设计模型进行改进，引入加权系数，调整结构初始造价及损失期望在目标函数中的相对重要性，并将改进的抗震优化设计模型用于SRC框架结构优化设计。

(2)考虑结构失效模糊性，从模糊可靠度概念出发计算结构在各性能水平失效时的模糊概率。可靠度模糊化内容主要包括建立结构、构件的模糊可靠度分析数学模型，改进考虑模糊性的Monte Carlo法。

(3)针对SRC框架结构优化设计的复杂性，将整体优化过程简化成两阶段，分别针对结构在小震、中震、大震作用下的性能优化。

(4)利用MATLAB编程，验证本文优化方法。结果表明，结构总费用随迭代次数增加而降低，并收敛于最优费用。可见本文优化方法有效、可行。

参考文献

[1]Ang A H S, Lee J C. Cost optimal design of R/C buildings[J]. Reliability Engineering and System Safety, 2001, 73:233-238.

[2]李刚, 程耿东. 基于性能的结构抗震设计—理论、方法与应用[M]. 北京：科学出版社, 2004.

[3]邓国专. 型钢高强高性能混凝土结构力学性能及抗震设计的研究[D]. 西安: 西安建筑科技大学, 2008.

[4]高小旺,刘佳,高炜. 不同重要性建筑抗震设防标准的讨论[C]. 北京：城市与工程减灾基础研究论文集[A].北京:中国科技出版社, 1997.

[5]王光远. 抗震结构的最优设防烈度与可靠度[M]. 北京: 科学出版社, 1999．

[6]Chan C M, Zou X K. Elastic and inelastic drift performance optimization for reinforced concrete buildings under earthquake loads [J]. Earthquake Eng. Struct. Dyn., 2004, 33:929-950.

[7]GB50068-2001,建筑结构可靠度设计统一标准[S].

[8]JGJ138-2001,型钢混凝土组合技术规程[S].

[9]GB50011-2010,建筑抗震设计规范[S].

[10]GB50010-2010,混凝土结构设计规范[S].

[11]陶清林,郑山锁,胡义,等. 型钢混凝土柱多目标优化设计方法研究[J]. 工业建筑, 2010, 11(40):126-130.

TAO Qing-lin, ZHENG Shan-suo, HU Yi, et al. Study on multi-objective optimization design method for SRC columns [J]. Industrial Construction, 2010, 11(40):126-130.

[12]Ringertz U T. On methods for discrete structural optimization [J]. Eng. Opt., 1988,13(1):47-64．

[13]Royset J O, Kiureghian A D,Polak E. Reliability-based optimal design of series structural systems[J]. Journal of Engineering Mechanics, 2001,127(6):607-614.