常利率复合负二项风险模型下稳定经营的必要条件

常利率复合负二项风险模型下稳定经营的必要条件

乔克林，高渊，张宁

(延安大学数学与计算机学院，陕西延安716000)

摘要：假设保险公司刚开始持有的资本为u，以常数δ为利率积累，并且保单总份数服从负二项过程，理赔总次数服从Poisson过程，给出常利率复合负二项风险模型以及稳定经营的必要条件。

关键词：常利率；双险种；复合负二项；稳定经营

中图分类号：O211.9

文献标识码：A

文章编号：1004-602X(2015)01-0007-02

收稿日期：2014-12-19

基金项目：陕西省教育厅自然科学基金(2010JK914)；延安大学教改项目(YDJG10-02)

作者简介：乔克林(1964—)，男，陕西佳县人，延安大学副教授。

Abstract：Assume that insurance companies began to hold capital to u,with constane δ is accumulation of interest rates,and policy number always obey hegative binomia process,manage compensate total number follows poisson process.we give the compound negative binomial risk model with constant interest rate and the requirement of insurance company working stably.

风险理论就是指在运行中的保险公司，在各种各样的损失的概率分布的基础上，进行精确的数理运算和数理分析的理论。它的核心在于模型的建立和数理方法的应用。而在各种模型中，带利率的模型难度较大。在以往的研究中，分别讨论了简单的Poisson过程模型[1-3]，二项过程模型[4-6]、负二项模型[7-9]等等。因此本文在此基础上，建立利率、保费的复合的负二项风险模型。会出现两种索赔，三种可能和风险公司稳定经营的必要条件。

1模型假设

(1)假设保险公司刚开始持有的资本为u,(u≥0)资本始终积累，并且是以常数δ(δ>0)为利率开始积累的。

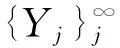
(4)当理赔发生时，下面三种理赔有并且仅有一种可能发生：

(1)如果只有第一种险种发生理赔；

(2)如果只有第二种险种发生理赔；

(3)如果两种险种都发生理赔。

上面三种事件分别发生的概率为p1，p2，p3，显然P1+P2+P3=1。

假设第一种险种的理赔额Z1，它的分布函数为H1(z)，均值为μ1；第二种险种的理赔额Z2，它的分布函数为H2(z)，均值为μ2；则第三种事件的理赔额的分布函数为H1*H2(z)，均值为μ1+μ2，且Z1和Z2相互独立。设第j次的索赔额为Dj=Z1jδ1+Z2jδ2+(Z1j+Z2j)δ3，其中δk为0-1随机变量，当δk=1时，表示第k种理赔发生，且对每次的理赔，有且只有一个δk=1，其所发生的概率表示为Pr(δk=1)=Pk，k=1，2，3。Zij表示第i种险种在第j次索赔时的索赔额，且它们之间相互独立，i=1,2。用D表示任

意的Dj，由全概率公式可得

D的分布函数表示为H(D)=P1H1(D)+P2H2(D)+P3H1*H2(D)，则E[D]=μD=P1μ1+P2μ2+P3(μ1+μ2)；

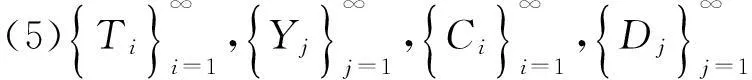
(6)存在r∞>0，使得当r→r∞时，有MD(r)=E(eDr)→∞。

2主要结果

2.1　模型定义

由以上假设，记在时刻n的盈余资本为：

由于破产只可能发生在理赔时刻，记为：τδ=inf{n,Uδ(τn)<0}，则模型在初始资本u下的破产概率为φδ(u)=P(T<∞)|Uδ(0)=u)；Ψδ(u)为模型在初始资金为u下的生存概率，则有Ψδ(u)=1-φδ(u) 。

2.2　保险公司稳定经营的必要条件

引理2[11]设{N(t)，t≥0}是参数为λ的Poisson过程，{Yn,n=1，2，…}是其为到达时间间隔序列，则Y1，Y2，…Yn，…相互独立且同服从参数为λ的指数分布。

定理1保险公司稳定经营的必要条件是：

μc-p1(λ-δ)μD≥0。

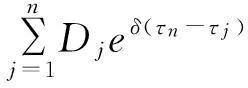
=S1eδ(τn-T1) +S2eδ(Tn-T2) +…+Sn

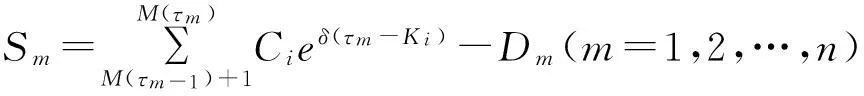
由引理和全期望公式可得到

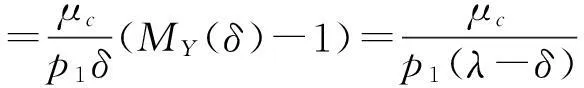
μc-p1(λ-δ)μD≥0。

参考文献：

[1]乔克林，李粉香.带利率的特殊双险种风险模型的破产概率[J].经济数学，2009，26(4)：824-828.

[2]方世祖，罗建华.双复合Poisson风险模型[J].纯粹数学与应用数学，2006(02)：271-278.

[3]蔡高玉，耿显民.带干扰的双复合Poisson风险模型[J].大学数学，2007(01)：110-112.

[4]乔克林，何树红，马乐荣.考虑投资收益率随机变化的复合二项风险模型的破产概率[J]延安大学学报(自然科学版)，2002，21(4)：13-19.

[5]龚日朝，杨向群.复合二项风险模型的破产概率[J].经济数学，2001(02)：38-42.

[6]乔克林，乔小宁，曹正江.常利率复合二项风险模型的概率分布[J].延安大学学报(自然科学版)，2014，33(1)：9-15.

[7]王丙参，魏艳华.保费收取次数为负二项随机过程的风险模型[J].江西师范大学学报(自然科学版)，2010(06)：604-608.

[8]魏丽.风险投资和大额索赔下更新模型的破产概率[J].中国科学(A辑：数学)，2009(08)：933-938.

[9]马建静，邢永胜.复合负二项风险模型下的破产概率[J].南开大学学报(自然科学版)，2008(01)：110-112.

[10]刘莉，茆诗松.常利率下风险模型破产问题的研究[D].华东师范大学博士学位论文，2004.

[11]张卓奎，陈慧婵.随机过程[M].西安：西安电子科技大学出版社，2003：57.

[责任编辑毕伟]

Requirement of Working Stably of Compound Negative

Binomial Risk Model with Constant Interest rate

QIAO Ke-lin,GAO YUAN,ZHANG NING

(College of Mathematics and Computer Science,Yan'an University,Yan'an 716000,China)

Key words：interest rate; two-type insurance; compound negative binomial; work stably