基于机械能变化的超低轨道大气密度实时估计

温生林，闫野

(国防科学技术大学 航天科学与工程学院，湖南 长沙410073)

0 引言

超低轨道是指大气层以外而又低于一般航天器轨道高度的空间区域。随着空间技术的发展和空间应用的深入，超低轨道飞行技术将成为航天领域的新兴发展方向。本文将超低轨道界定为120～300 km之间的飞行轨道。在此高度范围内，大气非常稀薄，但相对于外层太空而言，又存在大量气体分子，在卫星高超声速飞行时，气体分子撞击卫星的固壁产生作用力。对于运行于超低轨道上的卫星，地球非球形引力和大气阻力是主要的摄动力，尤其是大气密度相对传统卫星轨道而言显著增加。研究发现，在强大气阻力作用下，超低轨道会迅速衰减，大气阻力是制约超低轨道飞行的最主要因素［1］。同时，这一空间区域的大气密度随太阳活动、季节、地磁场、光照条件等因素的改变发生剧烈变化，大气密度存在较大的不确定性［2］。如何在轨实时获取大气密度是准确计算大气阻力、进行超低轨道飞行控制的前提。

当前，大气密度的确定方法主要有三种途径。一是基于经验的大气密度模型，常用的大气模型有:指数模型、改进的Harris-Priester模型、Jaccchia-71、Jaccchia-77、DTM、MSIS-90、JB2006 和 JB2008 模型［3］等。目前所使用的各种大气密度模型都属于半经验公式，且模型误差大约为10% ～20%，不能反映真实大气密度随太阳活动、地磁活动等因素的影响。另一种途径是利用最优轨道确定理论对现有密度模型进行修正［4-5］，其轨道确定是复杂的数学过程，计算量大，难以用于大气密度的实时估计。此外，也可以利用星载加速度数据和相关测量数据来计算大气密度［6］，这种方法除了要求进行高精度的加速度测量外，还要实现高精度的姿态测量与稳定控制，能够较准确地计算卫星的阻力系数。

本文对超低轨道卫星的大气密度估计问题进行研究，利用轨道动力学理论，分析了在地球引力、大气阻力和控制力作用下超低轨道卫星机械能的变化率，研究了如何利用能量变化实现大气密度估计。

1 大气密度估计方法

如图1所示，OXIYIZI表示地心惯性系，oxyz表示轨道坐标系，定义如下:

OXIYIZI:坐标原点O位于地心，以赤道面为基准面，OXI轴指向赤道平面上的平春分点，OZI轴垂直于平赤道面指向北极，OYI轴与OXI轴和OZI轴构成右手系。

oxyz:坐标原点o位于飞行器的质心，ox轴由地心指向飞行器，oy轴在轨道平面内垂直于ox轴，指向飞行器运动方向为正，oz轴与ox轴和oy轴构成右手系。

图1 坐标系定义Fig.1 Coordinate Systems

根据轨道动力学基本原理，卫星的角动量为:

轨道坐标系的坐标轴矢量可描述为:

轨道角速度ω= [ωxωyωz]T在轨道坐标系中的分量为［7］:

轨道坐标系的旋转角速度为:

可得:

地心距矢量r在轨道坐标系中可表示为:

对上式求导，可得卫星的速度:

卫星的加速度为:

另一方面，在地球引力、大气阻力加速度和控制力加速度作用下，卫星动力学方程为:

式中:U为引力势函数;fcontrol为控制加速度，fcontrol=为大气阻力。大气阻力加速度在轨道坐标系中的表达式为:

式中:ρ为大气密度;CD为大气阻力系数;A为迎风面积;m为卫星质量。

考虑中心引力和 J2项摄动，U的具体表达式为:

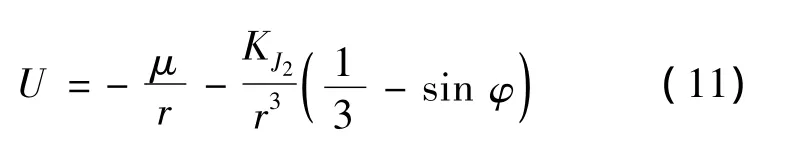
引力势函数的梯度为:

结合式 (8)～式(10)和式(13)可得:

角动量的变化率为:

卫星单位质量的动能为:

卫星的势能为U，根据式 (17)和式(11)，卫星的机械能为:

机械能的变化率为:

联合式(4)和式(15)，可得:

将式(14)、式(16)和式(20)代入式(19)，可得机械能的变化率为:

式(21)给出了在地球J2摄动、大气阻力和控制力作用下机械能变化率的计算公式，通过该式可知，机械能变化率与大气阻力和控制力有关，与J2摄动无关。事实上，地球引力是保守力，若没有非保守力的影响，在高阶地球引力模型作用下，卫星的动能和势能之和也是不变的。因此，在地球引力、大气阻力和控制力共同作用下，大气密度的计算公式可表示为:

2 仿真分析

本文以轨道高度为200 km的超低轨道卫星为例进行分析，仿真条件为:

(1)初始时刻超低轨道卫星的轨道根数为a=6 578.137 km，e=0，i=30°，Ω =0°，ω =0°，f=0°。轨道初始历元取为2012年6月1日12时0分0秒，仿真时间6 h，仿真步长1 s。

(2)卫星轨道计算采用STK软件HPOP轨道计算模型，考虑70×70阶EGM96引力场模型和大气阻力摄动，大气阻力系数CD=2.2，卫星质量为500 kg，面质比为0.02，采用Jaccchia-71大气密度模型，并将STK中的大气密度作为“真值”。

对超低轨道卫星在地球引力和大气阻力作用下利用卫星机械能的变化对大气密度进行估计，仿真结果见图2～图4。

图2 机械能变化曲线Fig.2 Mechanical energy changing curve

图3 机械能变化率的变化曲线Fig.3 The rate of mechanical energy changing curve

图4 大气密度估计值和“真值”对比Fig.4 Comparison between estimated and“true”densities

图2和图3分别给出了机械能和机械能变化率随时间的变化。由图可知，在大气阻力作用下，机械能不断减小，且呈现出波动性加速衰减的状态。图4表示大气密度随时间的变化，可以看出，大气密度的估计值和“真值”相一致，利用这种方法可以有效地估计出大气密度，与密度“真值”相比，估计得到的大气密度最大相对误差不超过5.89%。

3 结束语

本文研究了利用能量耗散率进行超低轨道卫星大气密度的估计方法。基于轨道动力学理论，分析了在地球引力、大气阻力和控制力作用下超低轨道卫星的机械能的变化特性，给出了利用能量变化实现超低轨道大气密度的估计公式。对典型超低轨道的大气密度估计进行了仿真，结果表明，这种估计方法是有效的，最大相对误差不超过8.29%。该方法所需的信息量少，仅需要超低轨道卫星的位置和速度信息，实现简单，对于超低轨道卫星进行轨道维持与姿态控制时需要获取高精度的大气阻力和气动力矩具有重要意义。

［1］ Atsushi N，Masanori H，Masayoshi U.The study of a super low altitude satellite［C］//Proceeding of 58th International Astronautical Congress.Fukuoka，Japan，2007.

［2］ George R G，Ronald JP，Paul JC.Requirements for accurate near-real time atmospheric density correction［C］//AIAA/AAS Astrodynamics Specialist Conference.Denver，CO，2000:1-17.

［3］ Vallado D A，Finkleman D.A critical assessment of satellite drag and atmospheric density modeling［C］//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Honolulu，USA，2008:1-29.

［4］ James R W.Optimal orbit determination［J］.Advances in the Astronautical Sciences，2002，112(2):1123-1134.

［5］ McLaughlin C A，Bieber B S.Neutral density determined from CHAMPprecision orbits［J］.Advances in the Astronautical Sciences，2008，119(7):167-186.

［6］ 陈光明，符养，薛震刚.利用星载加速度计数据反演高层大气密度的方法［J］.解放军理工大学学报，2010，11(3):371-376.

［7］ Chen Weiyue，Jing Wuxing.Differential equations of relative motion under the influence of J2perturbation and air drag［C］//AIAA SPACE 2010 Conference and Exposition.Anaheim，USA，2010:1-13.