一类热源在两端的反应扩散方程的边界控制

一类热源在两端的反应扩散方程的边界控制

郭春丽

(四川文理学院数学与财经学院，四川达州635000)

摘要：考虑了一类热源在两端的反应扩散方程反馈控制器的设计问题，利用边界控制的Backstepping方法设计出状态反馈控制器.由于热源在两端，反应扩散方程中含有两项反应项，因此，在运用Backstepping方法时，采用了改进后的Voltegral变换，利用偏微分方程的变量分离法求解出核函数，从而得到反馈控制器，进而证明了闭环系统的稳定性.

关键词：反应扩散方程；边界控制；Backstepping方法；稳定性

收稿日期：2015-04-01

基金项目：四川省教育厅2015年度资助项目“非线性反应方程的边界控制”(15ZB0325)

作者简介：郭春丽(1987—)，女，四川渠县人. 助教，硕士，主要从事应用数学研究.

中图分类号：O231.1文献标志码：A

0引言

生物学、化学和物理学中涉及到众多的数学模型，如半导体方程、生态方程、神经传导的Hodgkin-Huxley方程等，[1]这些都是有关反应扩散方程的问题，因而反应扩散方程有广泛的实际背景，从而也引起越来越多科学家们的注意，因此，近年来对反应扩散方程的研究也得到了极大的发展.[2-8]

在反应扩散方程的研究中，该方程的稳定性也是重要的研究方向，在早期的研究中，讨论较多的是这类方程的可控性或能稳性问题，而对具有能稳性的反应扩散方程，实际数学模型所需要的是使系统达到稳定的反馈控制器，但对控制器的设计问题则涉及较少. Krstic等人针对偏微分方程反馈控制器的设计问题，提出了偏微分方程边界控制的Backstepping方法，同时也提供了求反应扩散系统反馈控制器的方法，由于该方法计算简单且容易实现，近年来得到广泛的应用.[2-8]本文就运用该方法设计出一类热源在两端的反应扩散方程的反馈控制器.

1模型建立

热源在两端的反应扩散方程的控制系统如下：

ut(x,t)=uxx(x,t)+μu(0,t)+λu(1,t),x∈(0,1),t>0

ux(0,t)=0,t>0

(1)

ux(1,t)=U(t),t>0

其中，μ>0,λ>0是较大的常数(此时控制系统在不加控制的条件下是不稳定的)，u(x,t)表示温度，U(t)是反馈控制器.控制系统(1)描述的是热源在两端的热传导问题，这是由于控制系统(1)中反应项为μu(0,t)和λu(1,t)，这两项是关于左右端点的，也就是说热传导过程中热源在两端.

2状态反馈

首先，利用边界控制的Backstepping方法，用Voltegral变换将控制系统(1)转化为一个稳定的目标系统，然后利用该变换得到使控制系统(1)稳定的反馈控制器.

引入可逆的Voltegral变换：

(2)

其中，k(x,y)和r(x,y)是待定的核函数.[5-6]

变换(2)将控制系统(1)转化为指数稳定的目标系统:[2]

(3)

从而，由目标系统(3)和变换(2)可以得到使控制系统(1)稳定的反馈控制器.

2.1核函数的计算

为了得到反馈控制器U(t)，需要求解出变换(2)中的核函数k(x,y)和r(x,y).

为得到核函数的解，先由变换(2)将控制系统(1)转化为目标系统(3)，通过计算找到核函数需要满足的方程组，再由方程组进行求解.

首先，计算变换(2)关于x的一、二阶偏导数：

(4)

(5)

其中，

类似地，计算变换(2)的两边求关于t的偏导数，同时由控制系统(1)有：

运用控制系统(1)中的边界条件和分部积分法有：

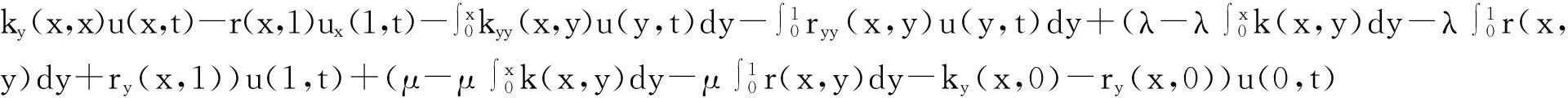
(6)

由(5)、(6)可得：

(7)

为满足目标系统(3)中的方程wt(x,t)=wxx(x,t)，因此，选择核函数满足如下方程组：

(8)

及相容性条件

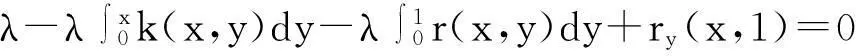
要使以上相容性条件同时成立，只要核函数k(x,y)和r(x,y)相容性条件

(9)

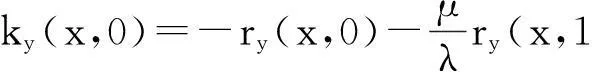
又由wx(0,t)=0、ux(0,t)=0及(4)式有：

于是，k(0,0)=0，rx(0,y)=0.由k(0,0)=0和k'(x,x)=0可得k(x,x)=0，因此，核函数k(x,y)满足方程组

从而，解得[2]

(10)

其次，为求解核函数r(x,y)，采用偏微分方程的变量分离法，设r(x,y)=p(x)q(y)，则p(x)和q(y)满足方程组

(11)

其中，a>0是待定的常数.

解方程组(11)可得

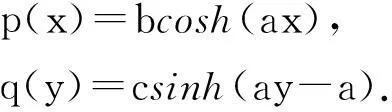
(12)

其中，b,c是待定的常数.

从而

r(x,y)=p(x)q(y)

=bccosh(ax)sinh(ay-a)

(13)

同时由(10)可得

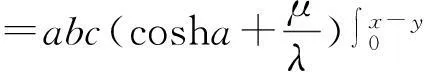
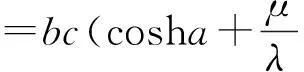
(14)

最后，利用(13)、(14)验证相容性条件(9)，得到待定常数a,b,c满足的条件，先由(14)有

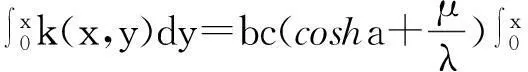
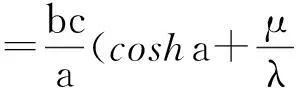
(15)

再由(13)得

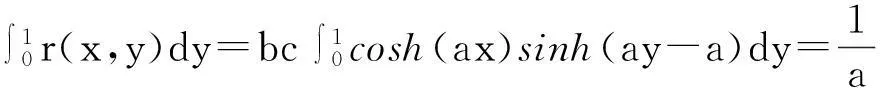
(16)

从而，由(15)、(16)及(9)可得

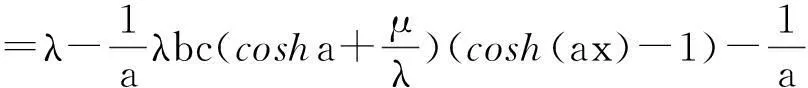
因此，要使相容性条件(9)得到满足，即是使上式恒等于零，于是取a,b,c满足如下条件

(17)

故只要a,b,c满足上式，便可使相容性条件得到满足.

综上可得，Voltegral变换中核函数k(x,y)和r(x,y)的解为(13)、(14)，其中常数a,b,c满足(17)式.

2.2反馈控制器

在(4)式中取x=1，同时由目标系统(3)中的边界条件wx(1,t)=0，可得控制系统(1)的反馈控制器U(t)：

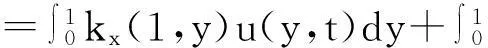
(18)

其中，核函数k(x,y)和r(x,y)由(13)、(14)给出，常数a,b,c由(17)给定.

3控制系统的稳定性

要证明控制系统(1)在反馈控制器(18)下是稳定的，需要得到可逆变换(2)的逆变换，该变换将稳定的目标系统(3)转化为控制系统(1).事实上，变换(2)的逆变换具有如下形式:

(19)

其中，l(x,y),h(x,y)是待定的核函数.

采用第2.1节的方法求出逆变换中的核函数，得到变换(2)的逆变换.最后由变换(2)和逆变换(19)的有界性及目标系统(3)的指数稳定性，选取合适的范数和能量函数，可证明原闭环系统(1)在反馈控制器(18)的作用下是指数稳定的.[6]

参考文献：

[1] 叶其孝，李正元. 反应扩散方程引论:第二版[M]. 北京：科学出版社，2011：174.

[2] M. Krstic,A. Smyshlyaev.BoundarycontrolofPDEs:Acourseonbacksteppingdesign[M]. SIAM, Philadelphia，2008：76-78.

[3] D. M. Boskovi, M. Krstic.Stabilizationofasolidpropellantrocketinstabilitybystatefeedback[J]. International Journal of Robust and Nonlinear Control, 2003(13):483-495.

[4] A. Smyshlyaev, M. Krstic.Closedformboundarystatefeedbacksforaclassofpartialintegro-differentialequations[J]. IEEE Transanction on Automatic Control, 2004(49):2185-2202.

[5] Z. C. Zhou, C. L. Guo.Stabilizationoflinearheatequationwithaheatsourceatintermediatepointbyboundarycontrol[J].Automatica, 2013(49): 448-456.

[6] C. L. Guo,C. K. Xie,Z. C. Zhou.Stabilizationofaspatiallynon-causalreaction-diffusionequationbyboundarycontrol[J]. Int. J. Robust.Nonlinear Control, 2014(27) :1-17.

[7] M. Krstic, B. Z .Guo, A.Balogh, etc.Output-feedbackstabilizationofanunstablewaveequation[J].Automatic ,2008(44):63-74.

[8] 郭春丽，周中成. 一类内部点级联的PDE-ODE系统的边界控制[J]. 控制理论与应用，2014(6):779-785.

[责任编辑范藻]

Boundary Control of a Reaction-diffusion Equation with the Heat Source

on the Both Boundaries

GUO Chunli

(Mathematics and Finance School of Sichuan University of Arts and Sciences, Dazhou Sichuan 635000, China)

Abstract:Consider stabilization of a reaction-diffusion equation with the heat source on the both boundaries by using boundary control. For the new equation, it contains two reactions. The Voltegral transformation of backstepping method is improved. And the kernel equations and computation are more complicated. Through the variable separation method of partial differential equations, the exact solutions of kernels are obtained, and a control law is obtained specifically. Finally, stability of the closed-loop system is established.

Key words:reaction-diffusion system; backstepping method; boundary control; stabilization