基于三端等效电路模型的FB-ZVZCS变换器控制环路设计方法

龙伟华，贲洪奇，孟 涛，陈 鑫

（哈尔滨工业大学电气工程及自动化学院，哈尔滨150001）

引言

平均电流型控制[1]因其良好的抗干扰能力、稳定性和电流控制特性，被广泛地应用于有源功率因数校正、蓄电池充电、POL（point-of-load）变换器和LED驱动等场合[2-4]。平均电流型控制方式的广泛使用，使得准确的系统模型对系统控制环路的设计至关重要。

文献[5-6]对平均电流型控制的系统建模采用了状态空间平均法[7]，忽略了电流补偿器输出信号上的开关纹波以及电流反馈回路的边频带效应[8]，造成模型在低频段不准确以及无法预测次谐波不稳定现象；文献[9]考虑了电流补偿器输出信号上的开关纹波，模型在低频段的准确性有所提高，但其本质上依然是平均模型，没有考虑电流反馈回路的边频带效应，依然无法预测次谐波不稳定现象；文献[10]借鉴峰值电流型建模方式，加入电流采样保持环节来分析平均电流型控制，但缺乏理论依据，模型准确性存在争议。

本文采用三端等效电路模型[11]对系统建模，获得系统准确的小信号等效电路模型。该模型考虑了电流补偿器输出信号上的开关纹波以及电流反馈回路的边频带效应，因此模型准确性高，可以预测次谐波振荡。基于该模型给出一种采用比例积分型电流补偿器的电流环设计准则，准确地量化了补偿器零点的位置、外加锯齿波斜率以及其他约束条件，避免传统设计方法存在的过补偿问题，获得了更宽的电流控制带宽。由于电源输出电压宽范围变化，系统难以保证全局稳定性，本文分析了稳态工作点对输出宽范围可调电源系统的影响，给出了系统穿越频率选取的依据，完成电压补偿器的设计，在保证系统稳定工作的同时，获得尽可能高的穿越频率，提高系统动态响应速率。

1 系统小信号建模

原边串饱和电感的全桥零电压零电流开关FB-ZVZCS（full bridge-zero voltage zero current switching）变换器拓扑结构如图1所示，其中Ls为饱和电感，Llk为变压器漏感。该变换器实质上是Buck电路，不同之处在于存在占空比丢失的问题[12]。

图1 原边串饱和电感的FB-ZVZCS变换器Fig.1 FB-ZVZCS converter with saturated inductor series in primary side

根据FB-ZVZCS变换器的工作原理，可获得副边有效占空比Deff与原边占空比D之间的关系[13]为

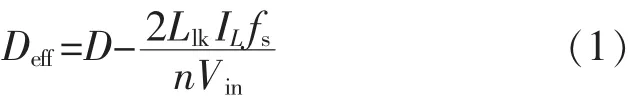
式中：IL为电感电流；fs为开关频率；n为变压器变比；Vin为直流母线电压。

对其加入小信号扰动，化简可得

图2 电流环等效拆分Fig.2 Equivalent separation of the current loop

占空比的丢失可近似地认为是在每一稳态工作点丢失一个恒定量，不影响变换器的小信号特性，因此，可将其简化为Buck电路进行分析，其电路图如图2所示。平均电流型控制的Buck电路如图2 （a）所示。依据等效替代的原则将电流环拆分为比例环节和积分环节，如图2（b）所示。图中，Ri为采样电阻；Se为锯齿波斜率；Ri′为等效采样电阻，Ri′=则电感电流上升沿斜率电感电流下降沿斜率

三端等效电路模型[11]如图3所示，模型包含主动开关、二极管、电感、PWM比较器和电流闭环。该模型将电路中所有非线性环节作为一个整体进行分析，对控制信号Vc加入频率为fp的扰动信号，从时域的角度出发推导电流闭环输出信号与扰动信号的关系，由于时域信号包括了扰动信号的所有边频带信号 kfs±fp（k=1，2，3，…），避免了平均模型从频域角度出发只考虑扰动频率fp而忽略其边频带效应所造成的模型不能预测次谐波振荡的问题；同时电流补偿器输出信号作为模型输入，其开关纹波特性直接体现在电流闭环输出的时域信号中，所以模型能很好地预测低频段特性。因此，三端等效电路模型准确性高，能够预测次谐波振荡。利用此三端等效电路模型对图2（b）中虚线框部分进行等效替换，可获得系统的小信号模型，如图4所示。

图4 平均电流型控制小信号等效电路模型Fig.4 Small-signal equivalent circuit model for average current control

通过图4可获得任何所需的传递函数。则控制电压到电感电流的传递函数为

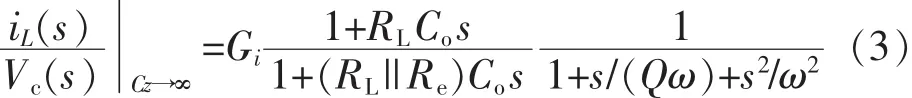
式中：RL为负载；Co为输出电容；ω 为角频率，ω=πfs；Q为阻尼系数，电阻Re=LQω；Gi为系数，

当电容CZ无穷大时，电流积分环路Tii不起作用，式（3）表现出峰值电流型控制的特性，其中低频零极点造成平均电流与峰值电流的误差；当电容CZ逐渐减小时，积分环路起作用，平均电流型控制与峰值电流型控制区分开来，双极点位于1/2开关频率处。双极点位置太近会造成次谐波振荡，阻尼系数Q表征双极点分离的程度，Q值决定平均电流型控制是否存在次谐波振荡。

2 电流补偿器设计

2.1 补偿器设计原则

电流补偿器的作用是使控制电压到电感电流iL（s）/Vc（s）的传递函数在尽可能高的频率内为一恒定增益，同时确保电流环稳定。补偿器设计步骤如下。

（1）根据积分环路增益确定零点位置。

电流环积分环节起到消除峰值电流与平均电流误差的作用。这一误差由式（3）中低频零极点造成，为消除该误差，电流积分环路Tii的穿越频率必须高于极点频率fp。极点频率fp为

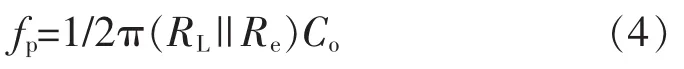
电流补偿器在零点频率之前主要是电容起作用，对电流误差进行积分；在零点以上频率处，电容

（2）确定补偿器比例系数。

由式（6）可以看出，为了使 iL（s）/Vc（s）为一恒定增益，补偿器产生的零极点应该相互靠近从而相互抵消各自的影响，因此RZ要远大于RA的值，例如RZ=10RA，但RZ与RA的比值不能过大，以免对运算放大器的增益带宽以及输出转换速率要求过高。

（3）选取斜坡补偿斜率 Se。

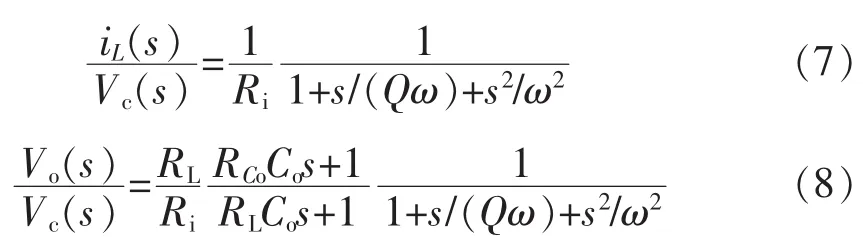
按照上述设计规则，控制电压到电感电流iL（s）/Vc（s）、控制电压到输出电压 Vo（s）/Vc（s）的传递函数可化简为：交流阻抗远小于电阻值，电流信号被比例放大，而没有积分作用。因此补偿器零点频率是积分环路Tii失去作用的转折点，所以补偿器零点应该放置在高于极点fp的位置，即

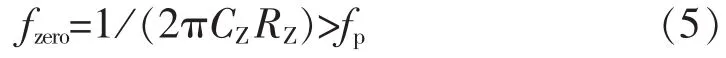
为保证充足的相角裕量，零点频率应远低于1/2开关频率。 当关系式（5）满足时， iL（s）/Vc（s）表达式为

式中：RCo为输出电容等效串联电阻ESR。

1/2开关频率处的极点对是由电流环比例环节的非线性造成的，平均电流型控制中的外加锯齿波的作用是抑制该极点对在1/2开关频率处形成尖峰，从而避免次谐波振荡。综合考虑电流环的环路带宽和稳定裕量，选取阻尼系数Q≈1时所对应的斜坡斜率较为合适，根据式（3）中Q值的表达式，可以获得锯齿波斜率为

文献[5，14]在电容 CZ和电阻 RZ支路上并联一个电容CP消除电流噪声尖峰。因采样得到的电感电流含噪声较少而且运算放大器增益带宽有限，电流补偿器输出Vcom相对干净，不需要强力滤波，而且CP的引入会产生一个高频极点，该极点会减小电流环路的稳定裕量以及损害其动态响应速率[15]。因此，为获得良好的电流调整特性，不建议添加该电容。

2.2 具体参数设计

全桥变换器主要参数为：输入电压三相380 V/50 Hz、输出电压50～600 V连续可调，最大电流4 A、开关频率 f=20 kHz、变压器变比 n 为 1.3∶2、滤波电感 L=3.62 mH、滤波电容 Co=575 μF（2 个 680 μF电容串联再与2个相串联的470 μF的电容并联）、电容等效阻抗Rco=0.135 Ω、等效电流采样电阻Ri′=0.047 3 Ω，电压采样系数KV=0.005 6。具体的参数设计如下。

（1）全桥拓扑等效为Buck电路，等效输入电压Vin和开关频率fs为

（2）选取 RA=1 kΩ；

（3）为使 RZ＞＞RA，选择 RZ=16 kΩ；

（4）积分环路 Tii的截止频率 1/（2πCZRZ）高于极点频率fp=2.5 Hz，同时截止频率不宜选太大，最终选取 CZ=0.22 μF；

电容 CZ=0.22 μF、CZ无穷大条件下 iL（s）/Vc（s）的Bode图如图5所示。图5（a）为Simplis仿真获得的结果，图5（b）为依据三端等效电路模型建模获得的结果。通过仿真与建模相对比，可以验证模型的正确性；同时积分环路Tii完全消除了低频段稳态误差，证明了积分环路设计的合理性。

图5 iL（s）/Vc（s）传递函数bode图Fig.5 Bode plots of transfer functions）/s）

（5）计算输出电压600 V时电流补偿器输出端放大后的电感电流上升斜率Snc和下降斜率Sfc，选取 Q≈1，带入式（9），计算出锯齿波斜率Se≈98 000 V／s，锯齿波峰峰值 Vpp=2.45 V。

3 电压补偿器设计

3.1 稳态工作点对系统影响

输出宽范围可调电源电压外环的设计需要考虑稳态工作点变化产生的影响。系统小信号模型中，传递函数中包括了稳态工作点的信息，改变稳态工作点的信息，就能分析出稳态工作点对系统的影响。

当变换器工作于DCM模式，系统比CCM模式具有更好的稳定性[5]；从式（8）可以看出，当变换器工作于 CCM 模式，负载大小仅对 Vo（s）/Vc（s）的低频段有一定影响，但在穿越频率附近没有影响；通过式（8）以及仿真分析验证可以得出，影响外环设计的关键因素是输出电压。

图6 给出了相同输出电流、不同输出电压条件下 Vo（s）/Vc（s）的 Bode 图，从图 6 和式（8）可以看出，输出电压减小，阻尼系数Q逐渐减小，位于1/2开关频率处的极点对分离程度增大，其中一个极点移动到 1/5 开关频率以内，给 Vo（s）/Vc（s）在穿越频率处带来过多的相位滞后。为保证系统的全局稳定性，电压外环设计应按最小输出电压这一稳态工作点进行设计。

图6 Vo（s）/Vc（s）传递函数Bode图Fig.6 Bode plots of transfer function Vo（s）/Vc（s）

3.2 电压补偿器设计

根据输出电压 50 V 时的 Vo（s）/Vc（s）设计电压补偿器。电压补偿器选取典型的Ⅱ型补偿器，如图7所示，补偿器的极点放置在电容ESR产生的零点位置，零点根据设定的穿越频率来确定，穿越频率的选取需考虑分离的极点对中频率较低极点的位置，由此可获得电压补偿器参数为R1=3 kΩ，R2=100 kΩ，C1=0.1 μF，C2=470 pF。 图 8 给出了系统补偿前和补偿后的开环传递函数bode图，电压外环穿越频率根据极点对分离程度选取在1/10开关频率处（4 kHz），补偿后系统的相位裕度为70°，系统具有良好的稳定性。

图7 典型的Ⅱ型补偿器Fig.7 Typical type Ⅱ compensator

图8 系统开环传递函数Bode图Fig.8 Bode plots of the open-loop transfer function

4 与传统电流内环设计方法对比

文献[2，5]中给出了传统平均电流型控制内环设计方法，该方法遵循电感电流下降沿斜率不能大于锯齿波上升沿斜率的原则。由该原则确定电流环的比例系数，电流补偿器的零点放置在1/2开关频率内，确定积分电容值，由此确定电流内环参数。图9为传统设计方法和基于三端等效电路模型设计方法下 iL（s）/Vc（s）、Vo（s）/Vc（s）的 Bode 图，传统设计方法下Sfc=0.80Se，Q=0.467；基于三端等效电路模型设计方法下Sfc=1.28Se，Q=0.933。从图中可以看出，基于三端等效电路模型的设计方法下电流控制的有效带宽是传统设计方法的 5 倍；Vo（s）/Vc（s）在（1/20～1/2）fs处的相位延迟更小，减小的相位延迟为提高电压外环带宽提供了可能性。传统电流内环设计中，补偿器零点的位置通常放置在1/2开关频率以内，没有给出具体的量化，新的设计方法准确地量化了零点的位置，避免了过高的零点损害电流环的相位裕度。

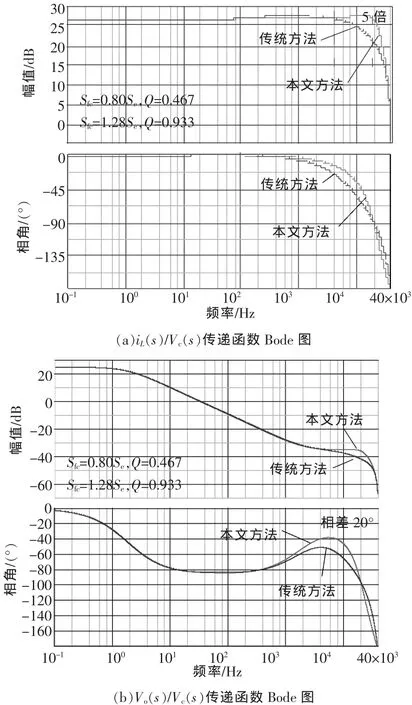
图9 2种设计方法的Bode图对比Fig.9 Comparison of Bode in two design methods

图10 为系统稳态工作时的Simplis仿真波形。由图可见，电流补偿器输出信号Vcom在开关管关断时期的斜率Sfc大于锯齿波的上升斜率Se。证明为避免次谐波振荡锯齿波斜率Se必须大于Sfc的观点是存在误区的，这实际上是一种斜坡过渡补偿。

图10 稳态工作时仿真波形Fig.10 Simulation waveforms of system in steady state

5 实验验证

按照上述设计方法，完成了最大电流4 A，输出电压50～600 V连续可调的FB-ZVZCS变换器控制环路设计，对系统进行性能测试，并给出了实验波形。

图11 为输出电压50 V，负载电流由2 A切换到4 A的动态响应波形。从图11（b）中可以看出，负载切换过程中输出电压最大跌落1 V，9 ms后系统重新达到稳态，稳态误差为0，说明系统具有良好的动态响应速度和稳定性。图12为输出电压600 V时，负载电流由1.2 A切换到3.2 A的动态响应波形。由图可见，负载切换过程中输出电压最大跌落1 V，动态响应速度约为6 ms，动态响应速度快，稳态误差为0。图11、图12表明，系统在宽输出电压范围内能够保证全局的稳定性，同时具有良好的动态响应速率，验证了设计方法的正确性。

6 结语

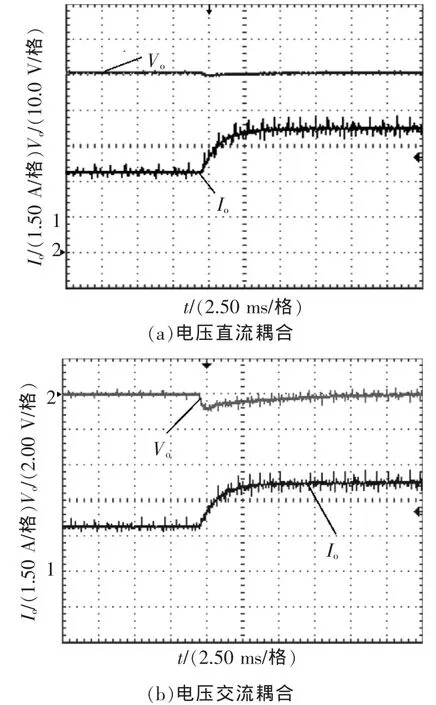
图11 输出电压50 V时负载切换的动态响应Fig.11 Dynamic response of load switching under output voltage of 50 V

图12 输出电压600 V时负载切换的动态响应Fig.12 Dynamic response of load switching under output voltage of 600 V

本文利用三端等效电路模型对输出宽范围可调电源进行系统建模，在此基础上给出了一种基于比例积分类型电流补偿器的设计方法，准确地量化了补偿器零点的位置、外加锯齿波斜率以及其他约束条件；分析了系统稳态工作点对环路设计的影响，得出了应选取最小输出电压这一稳态工作点进行电压外环设计的结论。仿真和实验结果验证了设计方法的正确性。

[1]苏瑞涛，米禹丰，贲洪奇.移相全桥ZVZCS变换器的数字控制与实现[J].电源学报，2011，9（6）：43-48.Su Ruitao， Mi Yufeng， Ben Hongqi.The digital control and realization of full bridge phase-shifted ZVZCS converter[J].Journal of Power Supply， 2011，9（6）：43-48 （in Chinese）.

[2]刘申月.基于平均电流型控制策略的微弧氧化电源研究[D].哈尔滨：哈尔滨工业大学，2009.Liu Shenyue.Research on microarc oxidation power supply based on average current mode control strategy[D].Harbin：Harbin Institute of Technology，2009（in Chinese）.

[3]Shin J W，Cho B H，Lee J H.Average Current Mode Control in Digitally Controlled Discontinuous-conductionmode PFC Rectifier for Improved Line Current Distortion[C]//The 26th Annual IEEE Applied Power Electronics Conference and Exposition.Fort Worth，2011：71-77.

[4]Texas Instruments.Average current mode PWM controller IC[EB/OL].http：//www.ti.com/lit/ds/slus231/slus231.pdf.

[5]Dixon L H.Average current mode control of switching power supplies[EB/OL].http：//www.ti.com.cn/cn/lit/an/slua079/slua079.pdf.

[6]Cooke P.Modeling average current mode control[C]//The 15th Annual IEEE Applied Power Electronics Conference and Exposition.New Orleans，2000：256-262.

[7]Robert W E.Fundamentals of power electronics[M].New York：Kluwer Academic Publishers，2001.

[8]Yan Y，Lee F C，Mattavelli P.Comparison of small signal characteristics in current mode control schemes for pointof-Load buck converter applications[J].IEEE Transactions on Power Electronics，2013，28（7）：3405-3414.

[9]Suntio T，Lempinen J，Gadoura I，et al.Dynamic effects of inductor current ripple in average current model control[C]//The 23nd Annual IEEE Power Electronics Specialists Conference.Vancouver，2001：1259-1264.

[10]Tang W，Lee F C，Ridley R B.Small-signal modeling of average current-mode control[J].IEEE Transactions on Power Electronics，1993，8（2）：112-119.

[11]Yan Y，Lee F C，Mattavelli P.Unified three-terminal switch model for current mode controls[J].IEEE Transactions on Power Electronics，2012，27（9）：4060-4070.

[12]吴彤.基于DSP控制的移相全桥ZVS变换器研究与设计[D].南京：南京理工大学，2014.Wu Tong.Research of phase-shifted full-bridge ZVS converter based on DSP controller[D].Nanjing： Nanjing university of science&Technology， 2014 （in Chinese）.

[13]阮新波.全桥变换器的软开关技术[M].北京：科学出版社，2013.

[14]陈轶涵，韦徵，龚春英.平均电流控制型移相全桥DCDC变换器输出阻抗及控制环路优化设计[J].电工技术学报，2013，28（4）：43-49.Chen Yihan，Wei Zheng，Gong Chunying.Study of output impedance and control loop optimization for average current mode control phase-shift full bridge DC-DC converter[J].Transactions of China Electrotechnical Society，2013，28（4）：43-49（in Chinese）.

[15]Yu F，Lee F C，Mattavelli P.A small signal model for average current mode control based on describing function approach[C]//IEEE Energy Conversion Congress and Exposition.Phoenix，2011：405-412.