电力变压器振动产生机理及影响因素研究

朱叶叶,汲胜昌,张凡,刘勇,董鸿魁,崔志刚,吴佳玮

(1.西安交通大学电力设备电气绝缘国家重点实验室,710049,西安;2.云南电网公司技术分公司,650000,昆明)



电力变压器振动产生机理及影响因素研究

朱叶叶1,汲胜昌1,张凡1,刘勇1,董鸿魁2,崔志刚2,吴佳玮1

(1.西安交通大学电力设备电气绝缘国家重点实验室,710049,西安;2.云南电网公司技术分公司,650000,昆明)

为了研究变压器振动的产生机理,针对饼式绕组结构的油浸式电力变压器,利用铁心和绕组的数学模型,分析了振动产生机理、合成过程以及不同运行工况对振动特性的影响。搭建了基于压电式振动加速度传感器的振动测试平台,针对变压器进行了空载、负载、功率因数、三项不对称度以及油温等变压器运行工况因素对于变压器振动特性影响规律的试验。结果表明:变压器最大分接时的基频振动分量大于额定分接时的基频振动分量;铁心以及绕组产生的振动信号在传递过程中并非线性叠加,箱体振动中基频分量随功率因数增加而增大;三相不对称运行状态下的变压器振动信号中存在50、150以及250 Hz分量;变压器箱体振动随油温上升呈线性增长趋势,且温度系数在0.005～0.035的范围内与变压器容量无关。研究结果为基于振动信号分析的变压器监测技术的进一步发展提供了参考。

油浸式变压器;饼式绕组;振动;功率因数;不平衡度;温升

作为电力系统的关键设备之一,电力变压器的正常运行对电网的安全可靠性起到决定性作用。变压器的历年统计资料表明,绕组线圈是故障重点部位之一[1-2],以2004年为例,全国110 kV及以上电压等级的变压器事故中由绕组故障引起的占69.8%,而引发事故的缺陷部分主要表现在铁心、线圈及引线、套管和分接开关。因此,对变压器绕组和铁心的状态进行监测具有重大意义。

90年代中后期,研究人员提出了基于变压器振动信号的变压器铁心及绕组状态监测技术[3-4],随后国内外展开了大量的研究,主要集中在振动信号采集系统的开发、振动产生机理的仿真研究以及振动信号的处理技术[5-17]。要实现基于振动信号的变压器状态监测,提取特征信号以及正确设置报警阈值是关键。变压器工作在一个多场耦合的环境中,其自身振动更是一个复杂的综合表现,振动信号中的故障信息容易受到变压器运行条件的影响,因此国内外学者对变压器振动特性的影响因素进行深入研究。文献[12-13]对变压器箱体振动基频分量与电压、电流及油温的关系进行了研究,并以此为基础初步提出了箱体振动数学模型;文献[14]提出了基于负载电流法的变压器振动监测方案。然而,影响变压器振动信号的不仅仅在于电流、电压及温度这3个因素,还包括测量位置、功率因数、三相不平衡度等。全面掌握非故障因素对变压器振动信号的影响规律,显然能够提高振动信号分析法故障诊断的正确率。

本文针对饼式绕组结构的油浸式电力变压器,深入研究了变压器运行电压、负载电流、功率因数、三相不平衡度、温升等运行工况的变化对其振动特性的影响和规律,探讨传感器安装位置、小幅错位时振动信号的变化以及风扇系统对油箱表面振动信号的污染情况。本文结论对基于振动信号分析的变压器状态监测技术的发展具有重要的参考意义。

1 变压器振动影响因素的理论分析

1.1 铁心及绕组振动机理

变压器振动是由于变压器本体(铁心、绕组等的统称)的振动及冷却装置的振动产生的[18]。铁心的振动主要由硅钢片的磁致伸缩现象以及涡流作用下硅钢片之间的相互吸引力引起。由于阶梯接缝以及无纬粘带在铁心绑扎方面的应用,目前变压器铁心的振动主要取决于硅钢片的磁致伸缩现象。假设电源电压U1=Ussinωt,根据电磁感应原理,铁心中产生的磁感应强度可表示为

(1)

式中:φ为铁心磁通量;B0=Us/(ωNS);S为铁心横截面积。

由于磁通密度和磁场强度呈线性关系,铁心中的磁场强度为

H=B/μ=BHc/Bs=B0Hccosωt/Bs

(2)

式中:Bs为铁心饱和磁感应强度;Hc为矫顽力。

在外磁场作用下,硅钢片由磁致伸缩产生的微小形变满足如下关系式[19]

(3)

式中:ε为硅钢片的轴向磁致伸缩率;ΔL为硅钢片轴向最大伸缩量;L为硅钢片原始轴向尺寸;εs为硅钢片的饱和磁致伸缩率。

综合上述关系可得,由磁致伸缩引起的铁心硅钢片轴向最大伸缩量为

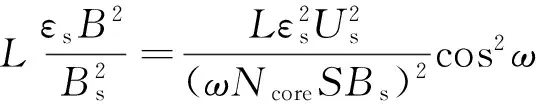
(4)

因此可得当变压器空载时,由硅钢片磁致伸缩引起的铁心振动加速度为

(5)

由式(5)可知,振动加速度在铁心材料、工作温度等条件不变的情况下与电压平方呈正比

(6)

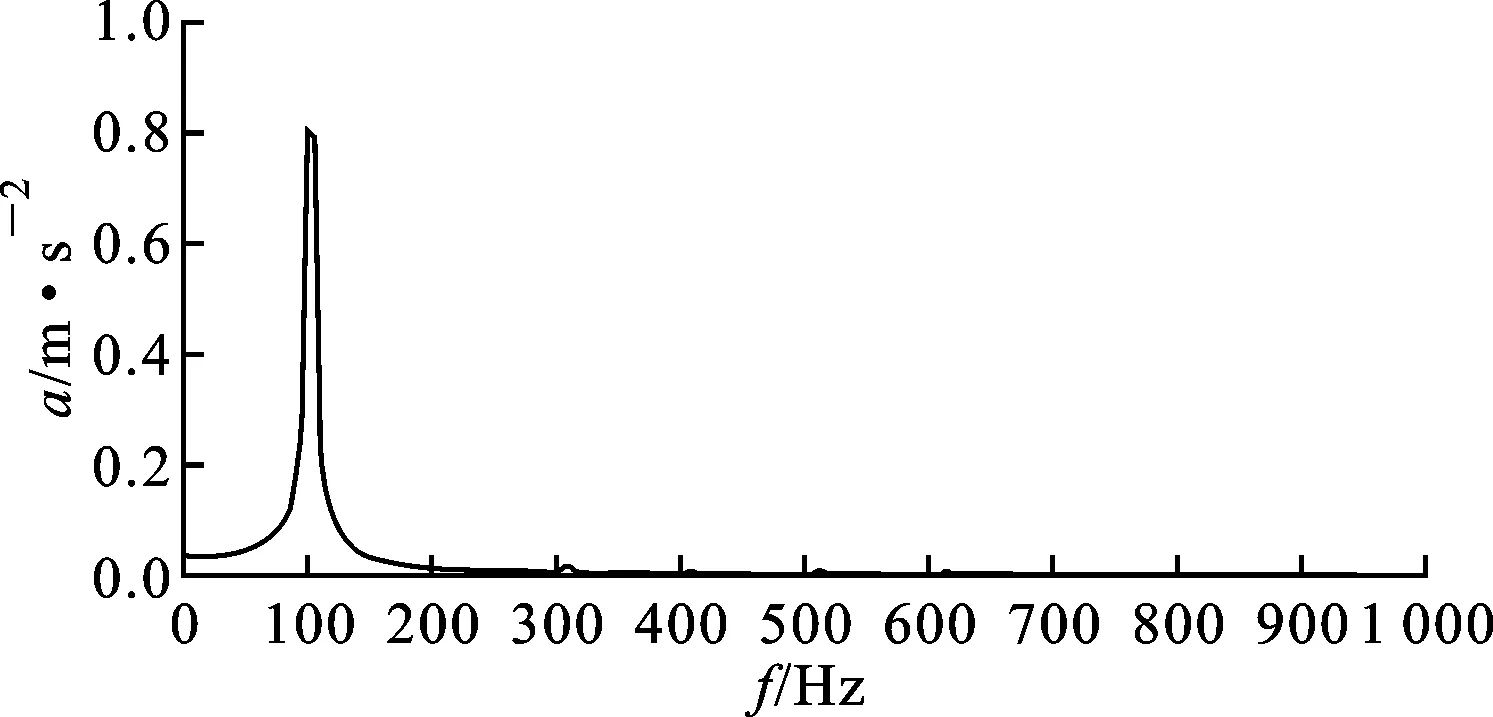
由于变压器铁心材料存在非线性等原因,实际中铁心磁通密度的波形并非标准正弦波,因此铁心振动信号中除了基频分量外,含有大量高次谐波成分。对于在频率为50 Hz的电力系统中工作的变压器铁心而言,除了基频100 Hz分量以外,200、300和400 Hz分量也较明显。由铁心硅钢片磁致伸缩的非线性造成的典型油浸式电力变压器空载振动频谱如图1所示。

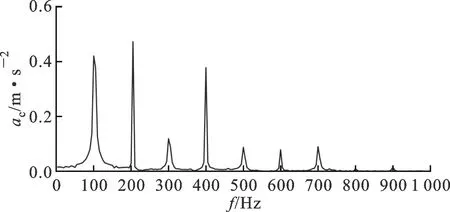
图1 变压器铁心典型振动频谱

当变压器绕组线圈中流过负载电流时,由于漏磁场的存在,绕组间、线饼间、线匝间产生动态电磁力,引起绕组的振动。假设稳定运行的电力变压器中流过绕组的电流I=Imsin(ωt+φ0),其中Im为负载电流幅值,φ0为负载电流初始相位,则作用在绕组线圈上的电动力为

(7)

式中:p为电动力系数。

变压器绕组线圈主要有饼式和层式两种结构,110 kV及以上电压等级的变压器主要采用饼式线圈结构[20]。在研究具有饼式结构的绕组的动态过程时,可将其视为由有弹性联系的实体所组成的机械系统。根据变压器绕组的机械结构,假设铁心的刚度为无穷大、绕组上下压板为刚性、线饼为集中的质量模块、绝缘垫块及端圈为弹性元件,将变压器绕组等效为弹簧质量系统[8-9],并根据动力学定理得出绕组位移的微分方程

(8)

式中:M为绕组线饼质量矩阵;C为阻尼系数矩阵;K为弹性系数矩阵。求解该方程组,可得绕组加速度

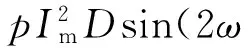
(9)

式中:ωa=(K/M)1/2;A和α由初始条件求出;D和β在固定条件下是与绕组参数有关的常数。

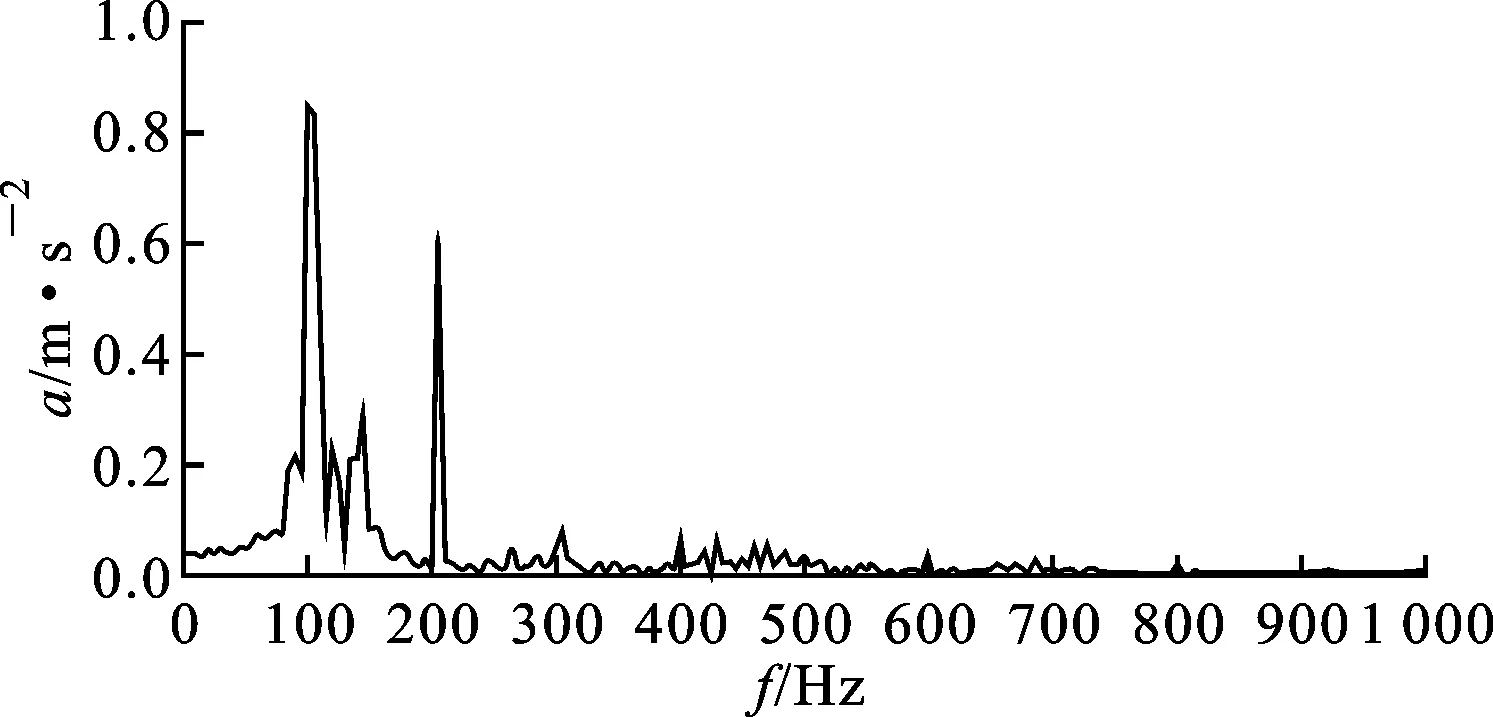
由理论分析可以得到,变压器绕组的振动由一个稳态分量以及逐渐衰减的分量组成,故在理想状态下稳定运行的变压器绕组的振动加速度信号也是电源频率的2倍(≈100 Hz)

(10)

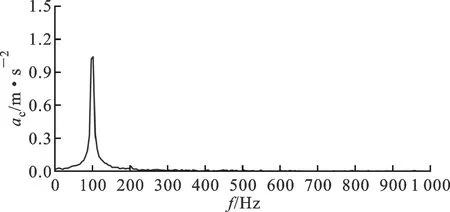
图2 理想情况中变压器绕组振动频谱

由式(10)可知,理想状况下电力变压器绕组振动加速度信号中仅有100 Hz分量(见图2)。实际情况中,由于变压器绕组绝缘垫块材料的非线性特性,绕组的振动信号中也可能存在100 Hz的倍频谐波。同时,在长时间带负荷运行中,由于紧固件松动、短路冲击等原因绕组会发生形变,振动频谱中的高次谐波随之逐步增大。

1.2 铁心及绕组振动合成

传统的变压器振动分析认为,铁心和绕组在相同运行条件下产生的振动互不相干,可线性叠加。振动理论指出,互不相干的各信号之间可线性叠加的前提是忽略相位差的影响[21],在变压器的实际运行中,功率因数一般不等于1,电流和电压之间存在相位差,变压器铁心及绕组所产生的振动加速度的相位差为

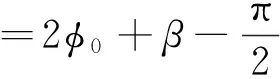
(11)

由铁心和绕组作为振源产生的振动在辐射过程中合成的振动加速度幅值为

(12)

由铁心振动及绕组振动合成的振动加速度满足

|ac|-|aw|≤a≤|ac|+|aw|

(13)

所以在不同的变压器结构参数以及运行功率因数下,铁心和绕组的振动矢量合成方式是变化的,在特定的条件下,由铁心和绕组振动的矢量和可能小于其中一个振动矢量的幅值。

此外,在交流电力系统中,三相不对称运行的情况时有发生。当系统不对称运行时,零序电流产生三次谐波[22],同时不对称相出现过电压,对变压器铁心及绕组的振动产生影响,铁心振动增大,三次谐波的入侵使得变压器绕组的振动频谱中也出现150 Hz的频谱。

1.3 油温对变压器振动的影响

在油浸式电力变压器振动的各影响因素中,油温变化是关键的一环。变压器油温对于振动的影响体现在两个方面:一是直接影响,温度的变化对于铁心硅钢片磁致伸缩率以及绕组绝缘垫块的弹性模量都存在影响;二是间接影响,温度变化对振动传递特性产生影响。

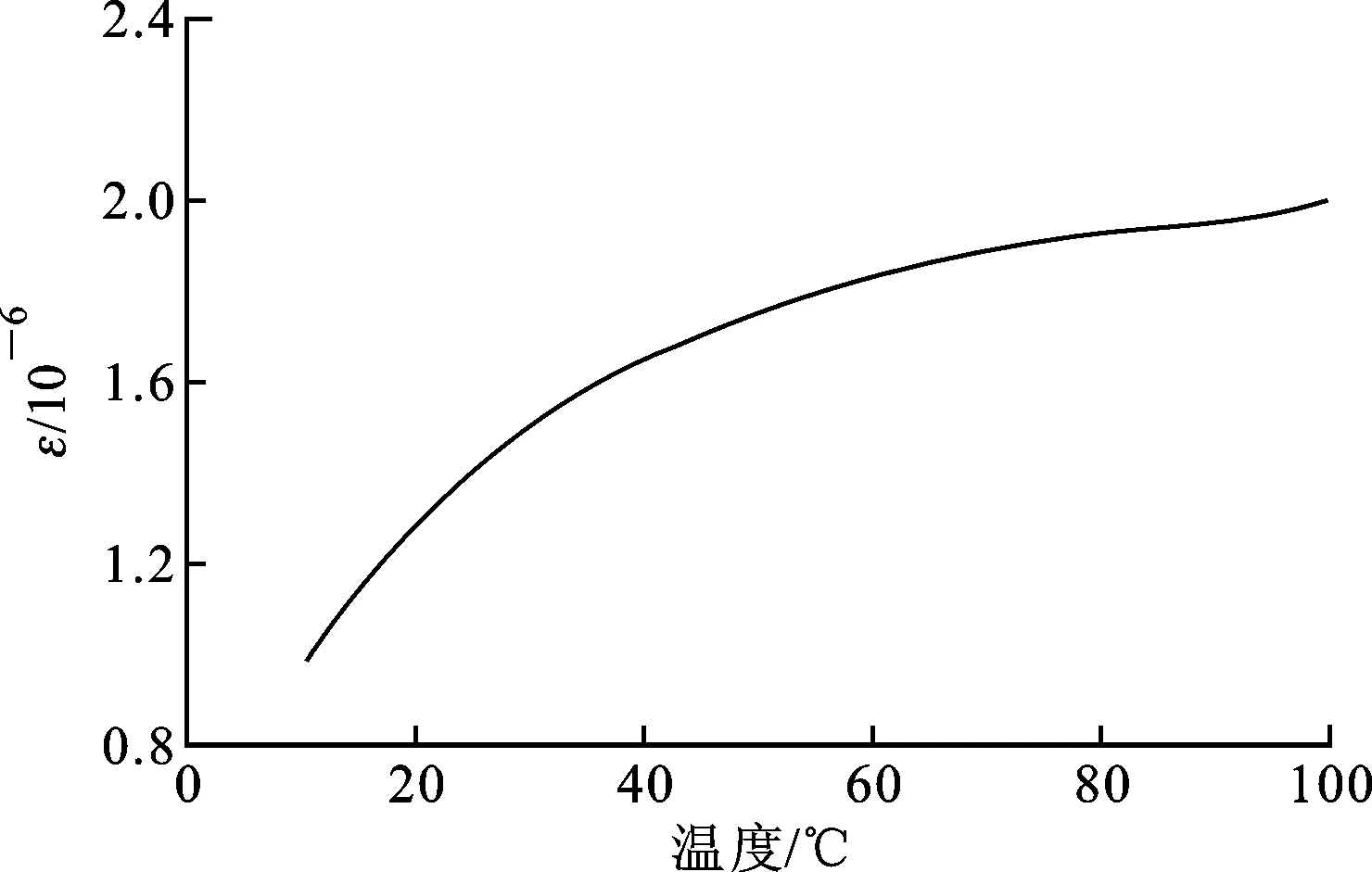
图3 温度对铁心磁致伸缩率的影响

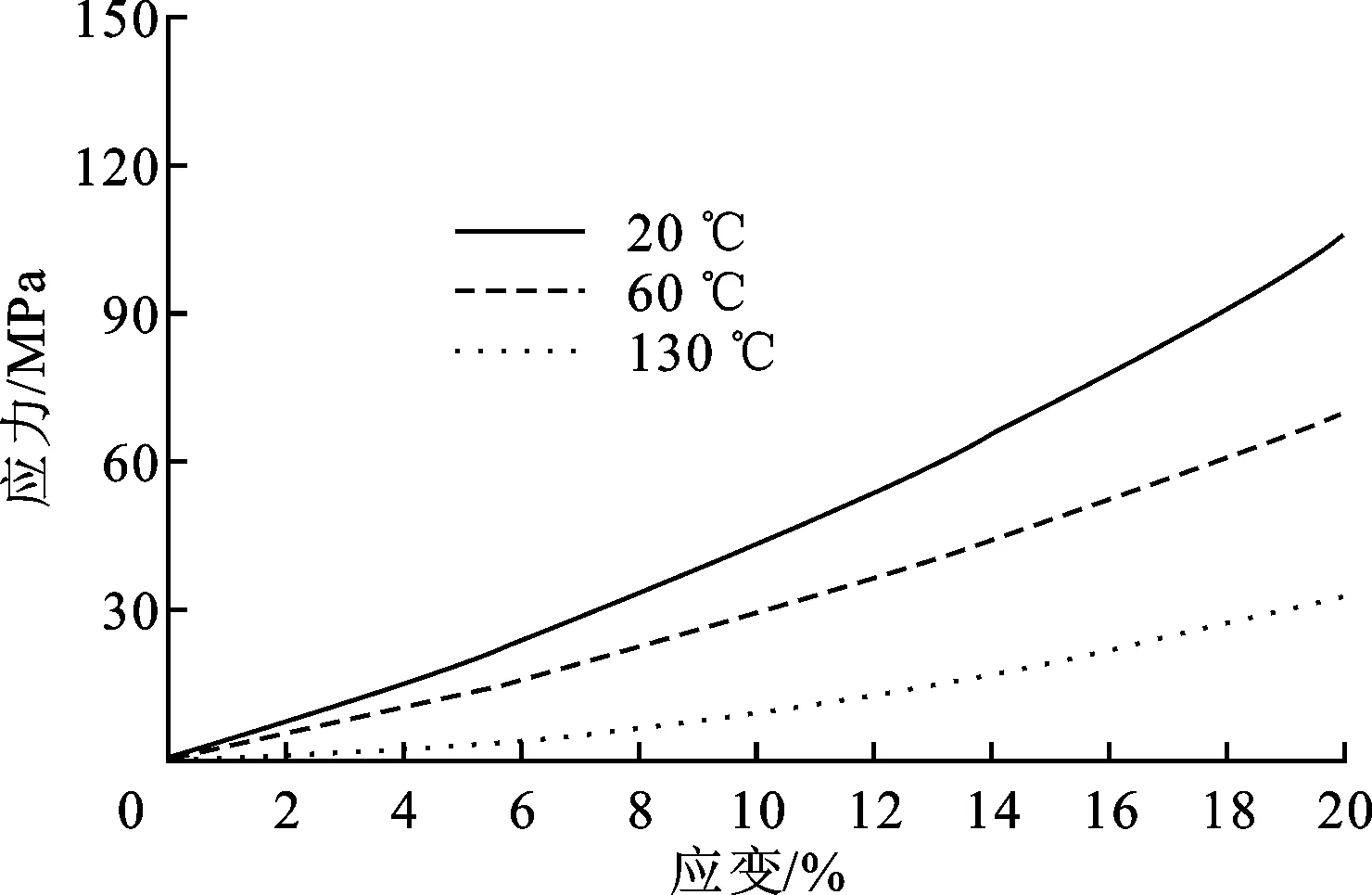
图4 不同温度下绝缘垫块的力学特性

根据相关机构的试验结果可知,磁致伸缩率ε随着硅钢片温度的升高而增大,铁心温度与磁致伸缩率的普遍关系如图3所示[20],因此油温升高时铁心振动加剧。以往的变压器振动理论分析认为,绝缘垫块是刚度渐硬的材料,在0～1 GPa的应力范围内弹性模量保持不变[9],然而实际变压器绝缘纸板的力学特性容易受到温度、湿度变化的影响,因此对不同油温浸泡下的变压器绝缘纸板力学特性进行了试验研究,应力、应变曲线如图4所示。由图可见,油温升高时,绝缘纸板的弹性模量下降,此规律对不同的绕组绝缘纸板来说具有普遍性。当绝缘纸板弹性模量下降后,绕组结构刚度产生变化,振动特性随之改变。

油温对变压器振动的间接影响表现在对于变压器油阻尼系数的影响以及热胀冷缩效应上。作为变压器绕组振动的传递路径之一,变压器油对振动信号存在阻尼作用[23],变压器油箱表面测得的振动信号是经过衰减的。变压器油的黏度由油分子间相互作用力产生,当油温升高时,分子间隙变大,结构松散,导致黏性减小,流动性增加,因此变压器油的黏度降低,渗透性变好,对绕组产生振动的阻尼作用有所降低,导致油箱表面测得的振动信号有一定程度的增加。变压器油的膨胀系数一般取0.000 7 ℃-1,当油温升高时热胀冷缩效应加剧油箱表面的振动信号。

2 变压器振动影响因素的试验研究

2.1 测试方案及其对变压器振动的影响

对于变压器绕组和铁心振动信号的采集,目前国内外基本运用的是压电式加速度传感器[5]和激光多普勒测振仪[6],后者的测量精度高,但代价也更昂贵,本文采用基于压电式加速度传感器的变压器振动测试系统。由于变压器箱体振动是一个复杂的综合反映,且变压器油箱的附件也存在谐振,因此不同的变压器测试方案(尤其是传感器安装位置)对测试结果存在巨大影响。

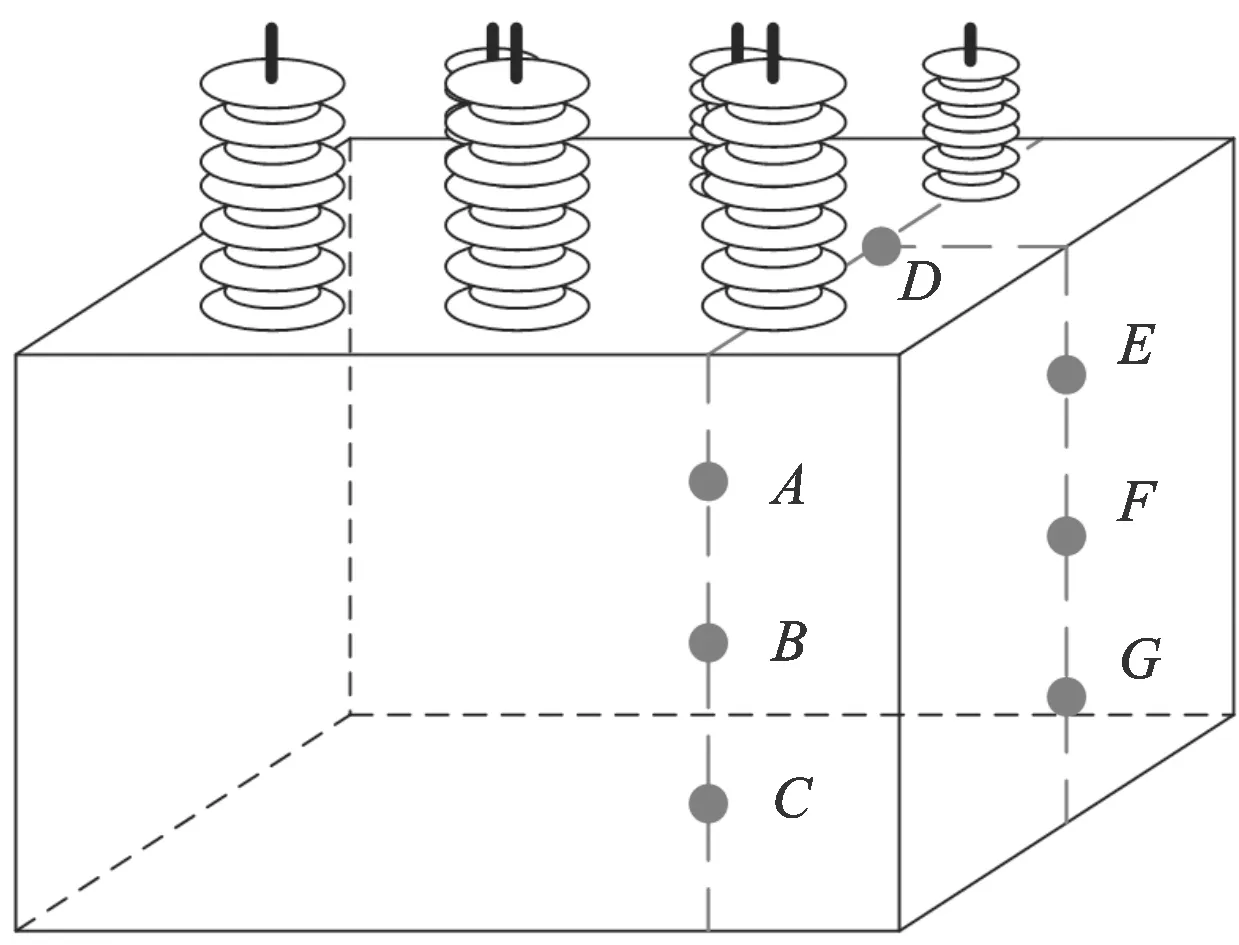
图5 传感器安装位置示意图

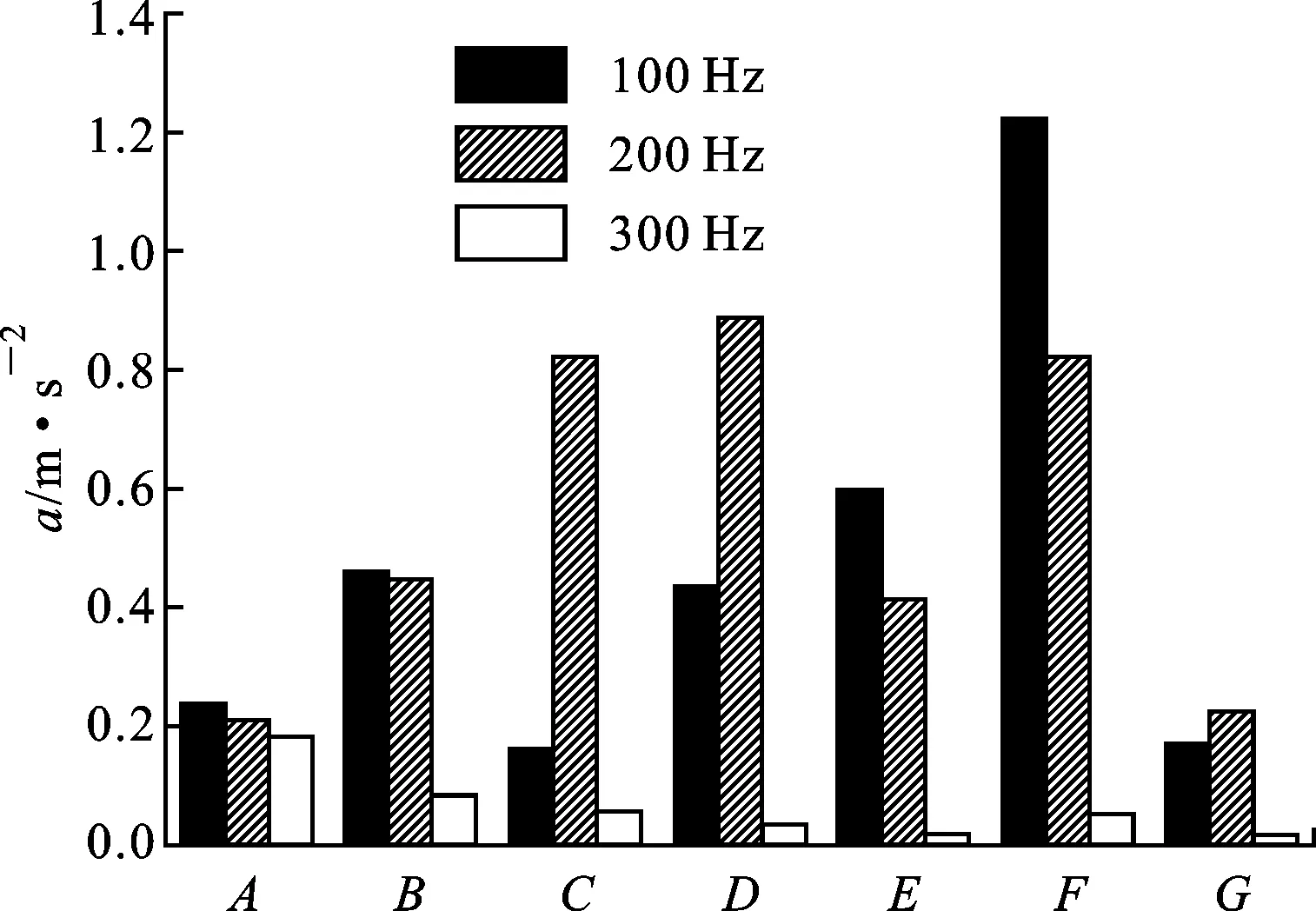
(a)振幅柱状图

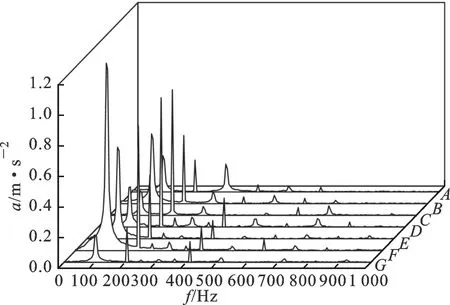
(b)振动频谱瀑布图图6 不同位置振动信号对比图

2.1.1 传感器安装位置 在变压器振动测试中,为测量传感器选择合适的位置是非常重要的。为了避免测得的振动信号被传播路径的频响特性所污染,振动加速度传感器的安装必须尽可能获得最直接的传播路径。对某试验变压器多测点进行了振动测试,测点分布如图5所示,以最直接传播路径为原则对A相绕组油箱顶部、前侧以及右侧分别选取了7个测试点。变压器稳定运行时各测试点处振动信号对比如图6所示。由图6可以看出:100 Hz基频处振动加速度分量F点远高于其余测点,但油箱顶部以及右侧测试位置的振动频谱中均出现奇次谐波,250及350 Hz分量较明显不能忽略;油箱前侧振动信号中无奇次谐波;C、D、F点处200 Hz谐振频率较大。综上所述,传感器安装位置对于振动信号的影响相当大,考虑到不同的变压器内部结构、外壳构造都有非常大的区别,在实际测试时应根据实际情况进行传感器布置。

2.1.2 传感器小幅错位 现场对变压器进行测试时,由于多种客观因素的影响,传感器的粘贴位置往往难以同前次测试保持完全一致,为了研究传感器粘贴位置对振动数据的影响,保证历史数据对比的可靠性,对模型变压器进行了传感器小幅错位时的振动特性测试。当传感器位置产生微小错位时,振动频谱的变化如图7所示。距离基准点3 cm处测点的振动频谱与基准点相近,6 cm处测点的振动频谱已出现明显差异,其中200 Hz频率处振幅变化最明显。相对于基准点位置对称的两测点处振动频谱相似度不高,证明传感器粘贴位置对振动信号的影响相当大。

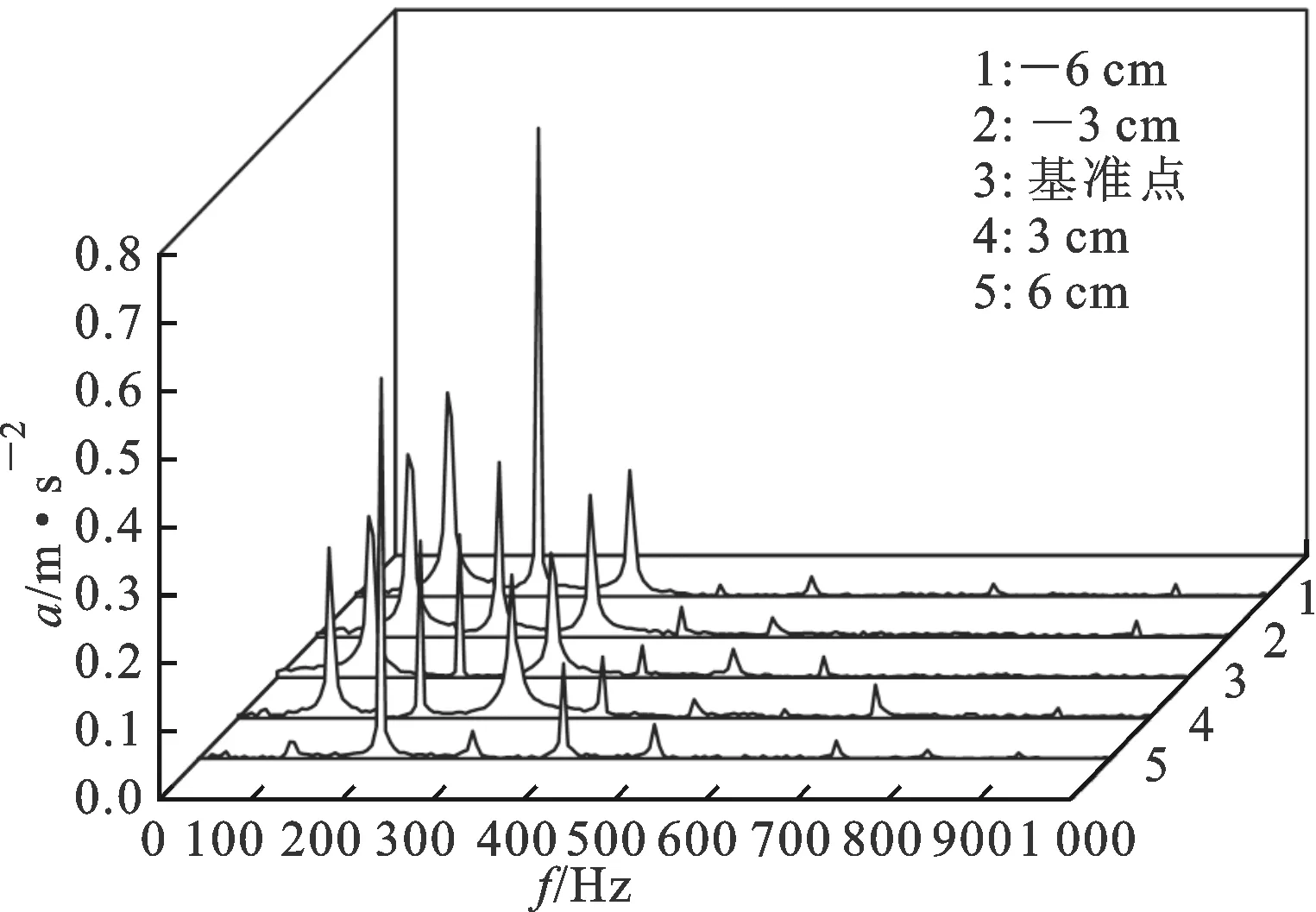
图7 传感器微小错位对振动频谱的影响

振动的强度可用振动加速度级表征,振动加速度级可用与噪声级类似的形式表示[21]

(14)

式中:a0为振动加速度参考值,针对变压器振动特性选择为10-3m/s2。

由式(14)得到图7中各点的振动加速度级,如表1所示,表中La1表示100 Hz振动加速度频率分量噪声级,La2表示200 Hz振动加速度频率分量噪声级,La3表示200 Hz振动加速度频率分量噪声级。

由表1数据可见,当传感器粘贴位置位移不超过±3 cm时,基频振动级数值变化在±1 dB内,视为可忽略的影响。因此,需要对同一台变压器进行多次振动测试时,建议给传感器粘贴位置进行标记。一般多次测试时不允许离开标记位置,如存在特殊情况,传感器安装位置离标记点也不应位移超过±3 cm,否则历史数据对比的可靠性存疑。

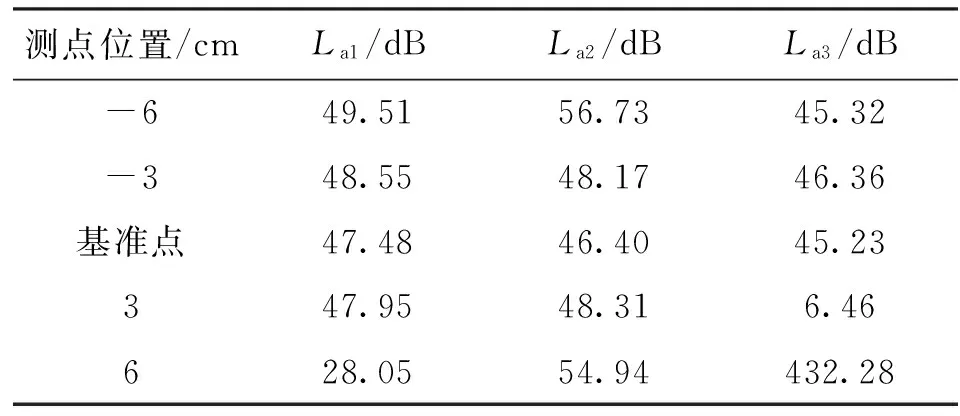
表1 传感器微小错位时的振动级

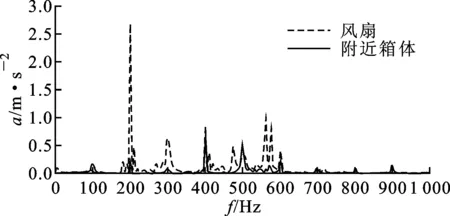
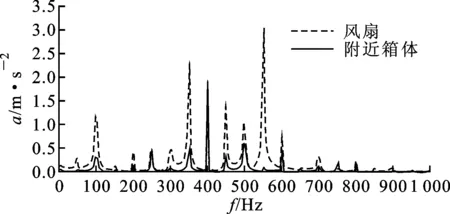
2.1.3 风扇制冷系统的影响 风扇及变压器冷却系统也是导致变压器振动的原因之一,而相关文献中提到,由风扇、油泵振动引起的冷却系统振动的频谱集中在100 Hz以下[5],可与以100 Hz为基频的变压器本体振动明显区分。在对某330 kV变压器进行振动测试时,4号风扇组(靠近高压套管一侧C相)启动后,A、B、C三相测点振动频谱如图8所示。从图8可得,远离运行中的风扇组的A、B两相振动频谱均未产生畸变,C相测点频谱受影响明显,100 Hz以及400 Hz频率附近出现畸变。因此,风扇系统对于变压器油箱表面振动的影响是不能忽略的因素。

(a)A相

(b)B相

(c)C相图8 风扇组开启后各相振动频谱

根据风扇组工作原理,运行中的风扇作为激励所产生的振动频率为

fb=rN/60

(15)

式中:r为风扇转速;N为风扇叶片数。

除了以上谐波外,风扇组内离散的叶片通过频率、变压器箱体的共振、容积激振以及宽带湍流等都会产生振动谐波。直接测试某220 kV及500 kV变压器风扇组表面振动信号,并与该风扇组附近油箱表面振动信号进行对比,如图9所示。结果图9a中200 Hz频率处风扇组振幅接近3 m/s2,附近变压器振动信号中却未出现大峰值的200 Hz分量,认为风扇组本体的固有振动频率处的幅值远大于变压器本身的振动,但风扇组的振动对附近变压器振动信号幅值的影响不显著。风扇组对附近变压器振动信号频率的影响从图9b可以得出,变压器振动频谱中出现和风扇本体振动一致的奇次谐波。因此,投运中的电力变压器振动频谱中奇次谐波的产生除了直流偏磁效应、测量系统干扰等原因外,也可能是由风扇组的运行导致的。因此,在选择振动加速度传感器安装位置时,应避开风扇组附近的位置,可保证变压器振动信号不受其污染。

(a)220 kV三相变压器

(b)500 kV单相变压器图9 风扇组对变压器振动信号的影响

2.2 变压器运行条件对其振动的影响

被试模型变压器为三相油浸自冷式冷却的双绕组变压器,额定容量为50 kV·A,额定电压为10 kV/400 V,额定电流为2.3 A/72.2 A。

2.2.1 空载特性及负载特性 根据前述的变压器振动产生机理,铁心振动与运行电压的平方成正比。对试验变压器进行空载试验,试验中变压器振动仅由铁心产生,箱体振动特性变化如图10所示,其中UN为额电电压。由图10可得结论,随着空载电压的上升,各频率处振幅均呈现上升趋势,基频分量的幅值与运行电压平方成正比,200、300和400 Hz谐振频率处振幅变化趋势不规律,这是由引起这些高次谐波的铁心的磁致伸缩效应现象中所存在的非线性引起的。

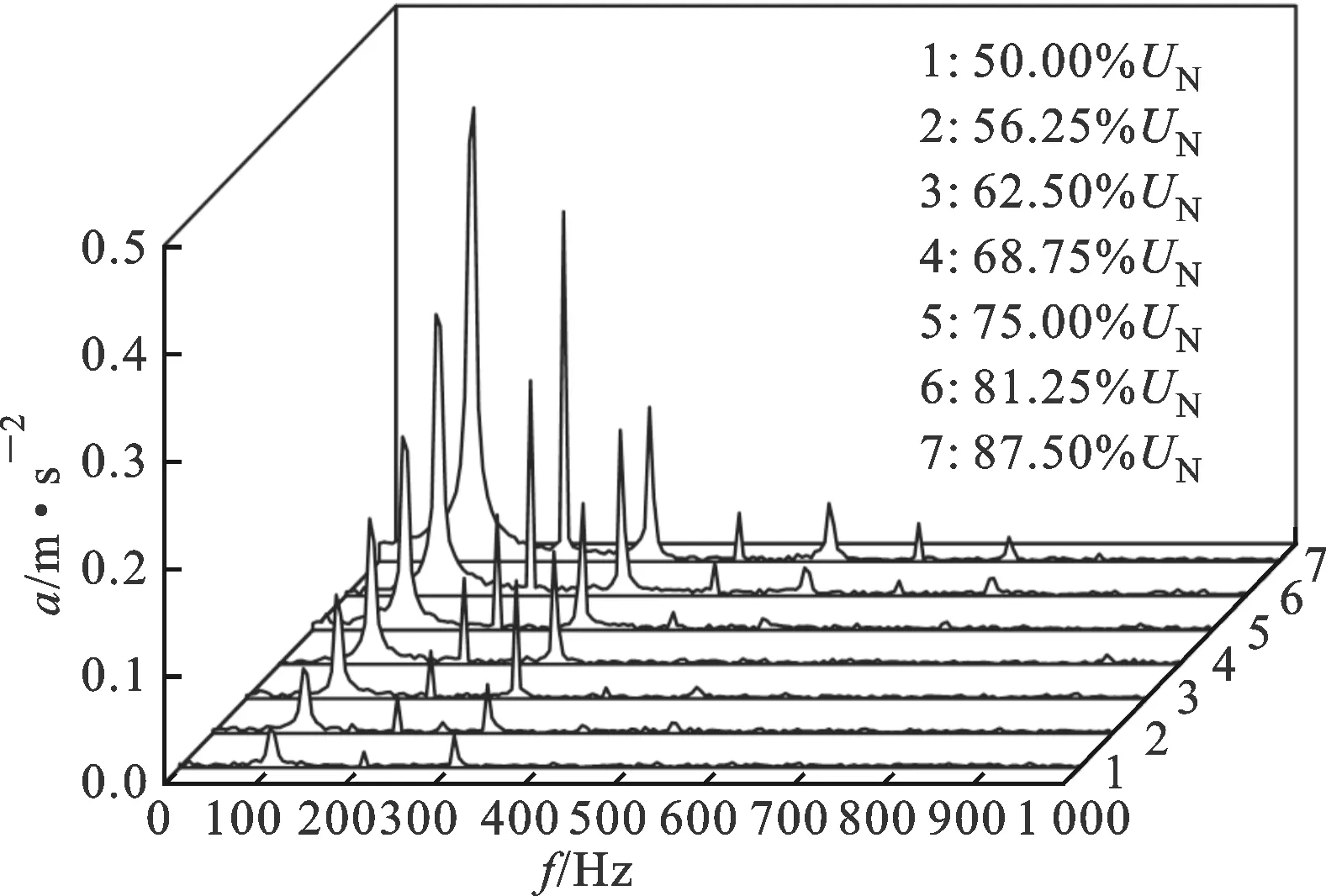
(a)振动频谱瀑布图

(b)振幅变化趋势图10 空载时运行电压对振动特性的影响

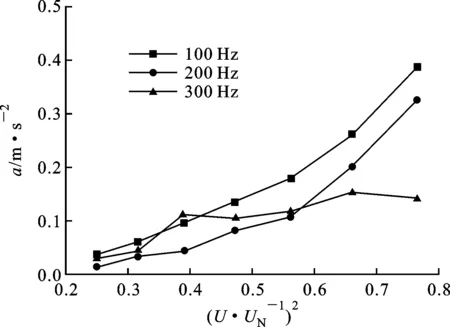
不同运行工况下振动基频分量对比情况如图11所示,模型变压器所用负载为纯阻性负载,而站内运行的电力变压器功率因数接近1。由图11a结果可知,对于模型变压器,负载时的箱体振动基频幅值小于空载时,负载越大,基频振动分量越小,但基频分量仍然与负载电压(电流)平方呈现近似正比关系。根据变压器振动理论,变压器铁心振动主要由铁心主磁通来决定,因此当绕组线圈中流过交变电流时,变压器内部产生漏磁场,涡流效应、集肤效应等现象可能对铁心的磁场分布产生抑制,因此表现为箱体振动在绕组通有负载电流时低于变压器空载时。

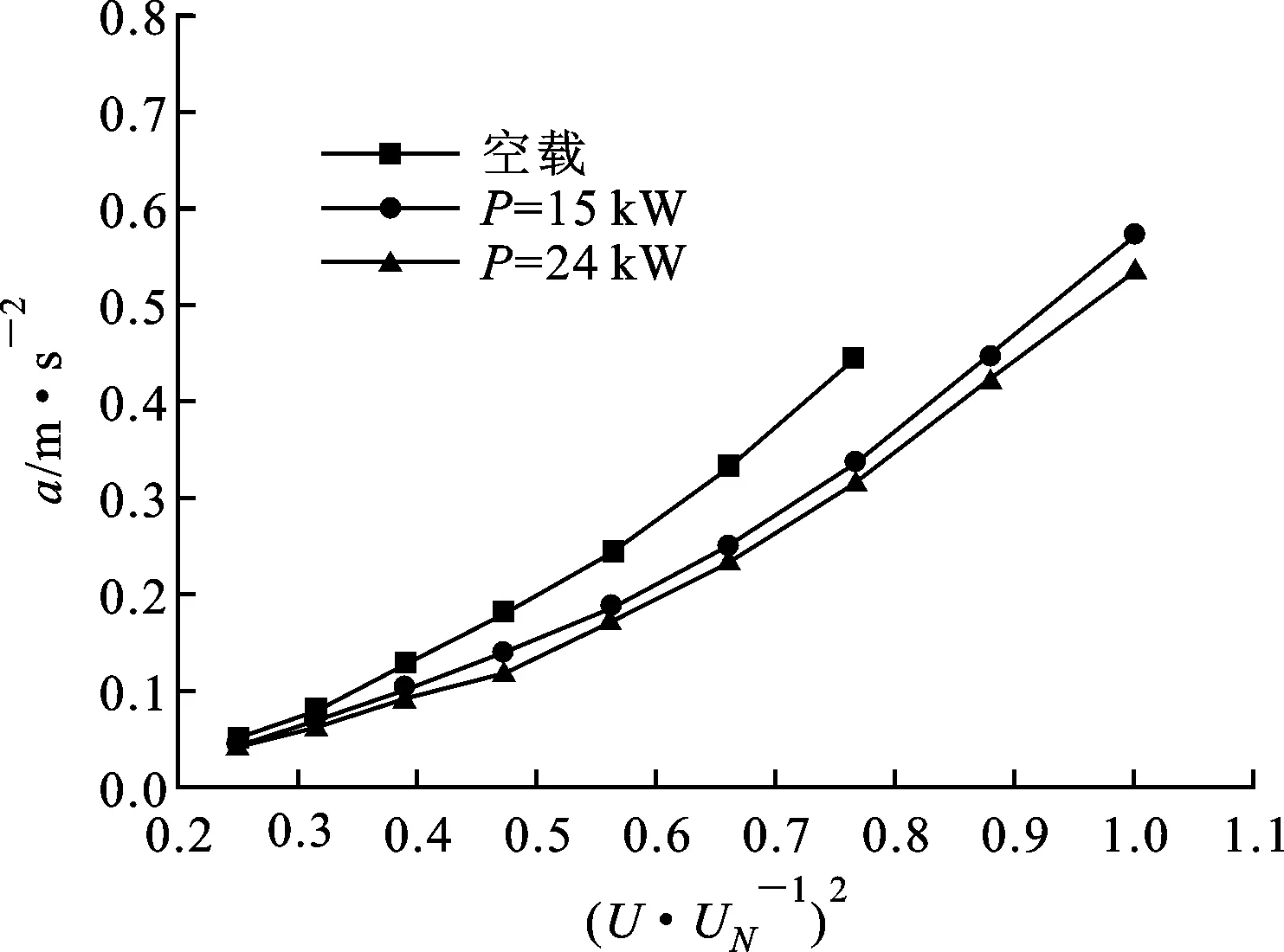
(a)额定容量为50 kV·A试验变压器

(b)额定容量为40 MV·A电力变压器图11 空载及负载下基频振动特性对比

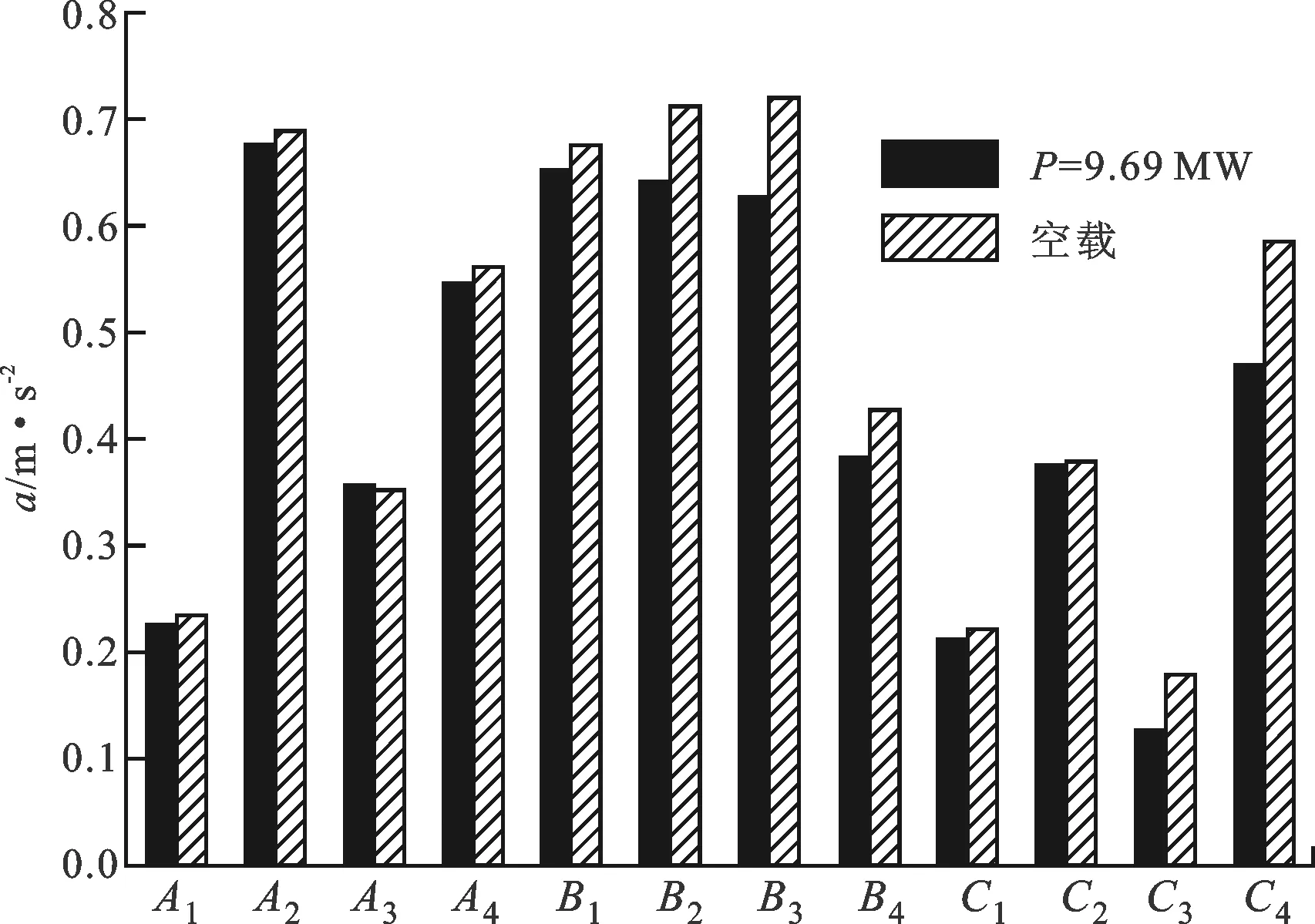
对于站内运行的电力变压器(测试结果如图11b所示),高低压套管侧各布置6路传感器,其中A1对应A相高压套管侧上端测试点,A2为下端,A3则对应低压侧上端测点,A4为下端,B、C相以此类推,不同位置处变压器空载时基频分量高于负载时,但增长的量较小,从另一侧面反映变压器正常运行中绕组振动幅值远小于铁心振动。

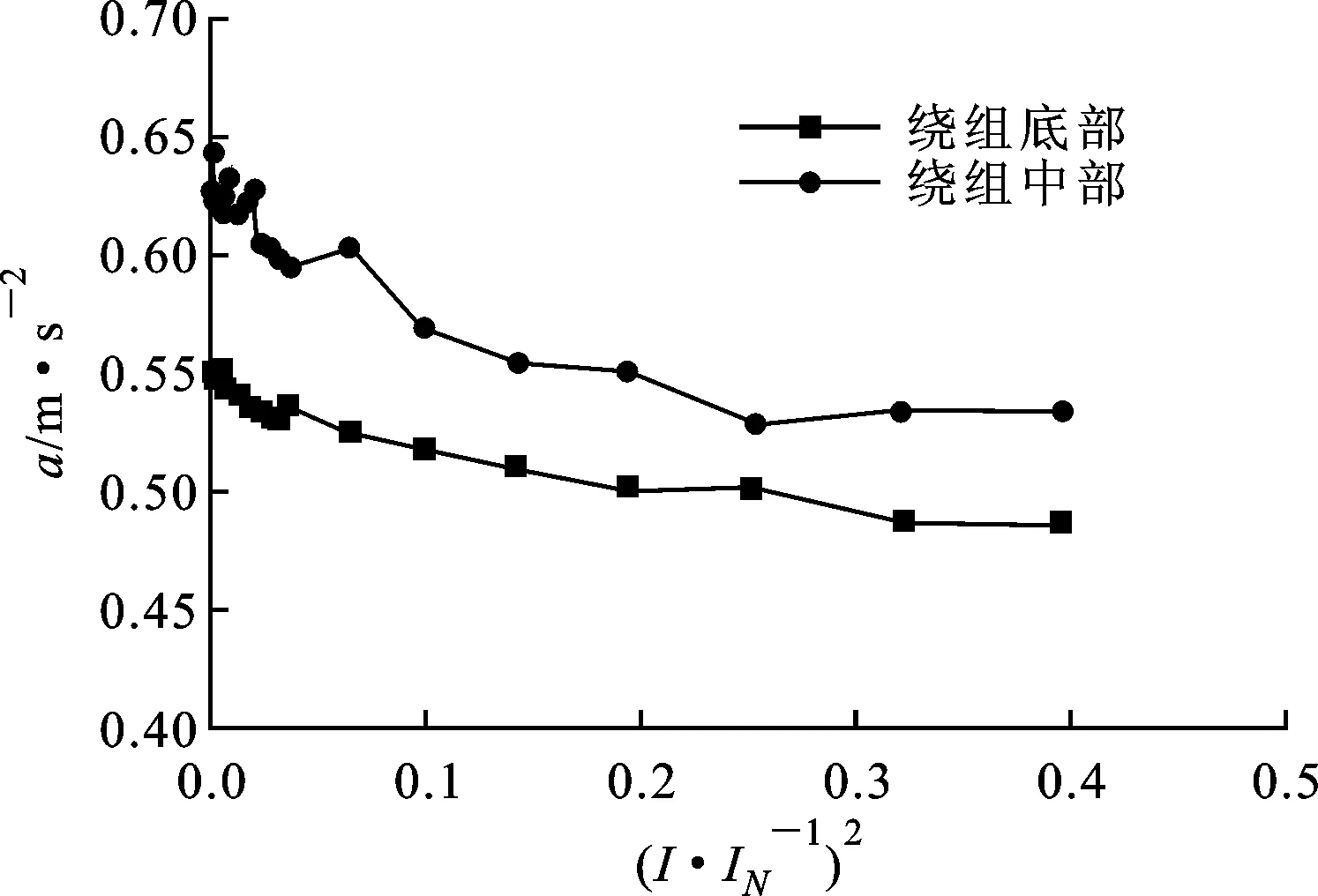
图12 负载电流对振动特性的影响

在带纯阻性负载运行的条件下,保持运行电压不变,通过改变负载来改变负载电流,基频处振幅变化趋势如图12所示。对于模型变压器,绕组在垂直于变压器油箱侧面的方向上基频振动随负载电流的升高而下降,并呈线性关系。同一绕组不同部位的基频振幅不同,但随负载电流水平变化的趋势一致。随着负载电流水平的升高,漏磁场对铁心磁通的抑制作用就越明显,由铁心所产生的振动就越小。稳态运行时,绕组振动与铁心振动相比偏小,作为铁心与绕组振动的综合反映的箱体振动则会表现出降低的趋势。

2.2.2 分接开关位置的影响 在实际电力变压器上,高压绕组一般设置有多个抽头,抽头与分接开关相连,通过分接开关与不同的变压器绕组抽头连接来改变变压器高低压绕组的匝数比,从而达到调节变压器输出电压的目的。对某具有5档分接的变压器进行振动特性测试,保持负载不变改变运行电压(负载电流随之变化),不同分接开关位置下同一测点基频振动分量特性如图13所示。分接开关位置对变压器振动的影响实质上是运行电压对铁心振动的影响,最大分接位置时变压器油箱表面振幅大于相同负载电流下额定分接位置的振幅,与理论分析一致,基频振动与电压平方呈线性关系,不同分接位置下斜率相近。

图13 分接开关位置对振动特性影响

2.2.3 功率因数的影响 在电力变压器的运行过程中,当变压器绕组中通过电流时,在电流与漏磁场的作用下,绕组内产生电磁机械力,其大小决定于漏磁场的磁通密度与导线电流的乘积,而力的方向由左手定则决定。为研究变压器箱体表面振动情况与流过绕组的负载电流相位的关系,给模型变压器分别施加相同容量的纯阻性、容性及感性负载,3种试验条件下变压器振动级随运行电压变化趋势如图14所示。在垂直于变压器油箱表面的振动方向上,3种试验条件下相同测点的振动特征频率相同,不同频率处振幅有所区别,100 Hz处容性负载振幅最大,感性负载其次,200 Hz处感性负载振幅最大,300 Hz处阻性负载振幅最大。

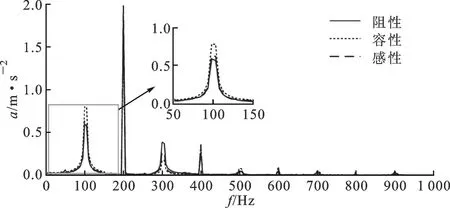
图14 不同负载下变压器振动频谱

在变压器实际运行中,功率因数并非固定不变的,上述试验证明了负载电流的相位对油箱表面的振动信号存在影响。为了探究功率因数的变化对变压器振动特性的影响,在保证负载阻抗值不变的前提下,调节负载电阻及电感的数值以模拟变压器负载功率因数的变化,振动特性随功率因数的变化如图15所示。从图中可以看出,在100及300 Hz处,振幅随功率因数上升而增大,而200 Hz处振幅随功率因数变化不大。另外,同测点的基频振动随功率因数增加呈上升趋势,但该趋势是非线性的。图15所示证明,变压器的振动特性与其运行的功率因数关系密切,基频分量幅值随功率因数的变化趋势符合式(11)的理论分析,在变压器振动监测的实际应用中不能忽略功率因数的影响。

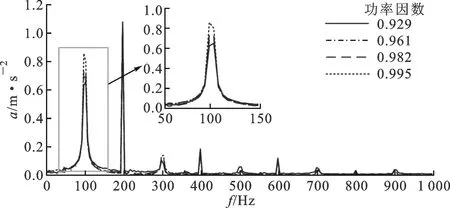
(a)振动频谱

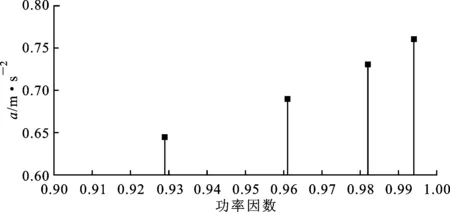
(b)基频振幅图15 功率因数对振动特性的影响

2.2.4 系统不对称运行的影响 在电力系统的运行中,由于三相元件、线路参数的不对称,电力变压器可能会运行在三相不对称的工况下,本小节研究了此类工况运行对变压器振动特性的影响。

在B相不对称运行度为30%的情况下,变压器振动频谱如图16所示。与对称运行的情况相比,各相振动频谱中出现50、150以及250 Hz的频谱分量。A、C两相在基频以及200和300 Hz处频谱分量下降,400 Hz处分量上升。B相作为不对称相,由于存在严重的过电压现象,200、300 Hz谐振频率处的振动分量增大,而100 Hz基频振动幅值较对称运行时减小。调节B相负载改变变压器三相运行不平衡度进行振动测试,可得不对称相(B相)各频率处振动分量随不平衡度变化的趋势,如图17所示。基频分量随不平衡度的增加下降,200及300 Hz铁心谐振分量随三相不平衡运行度增大而升高。

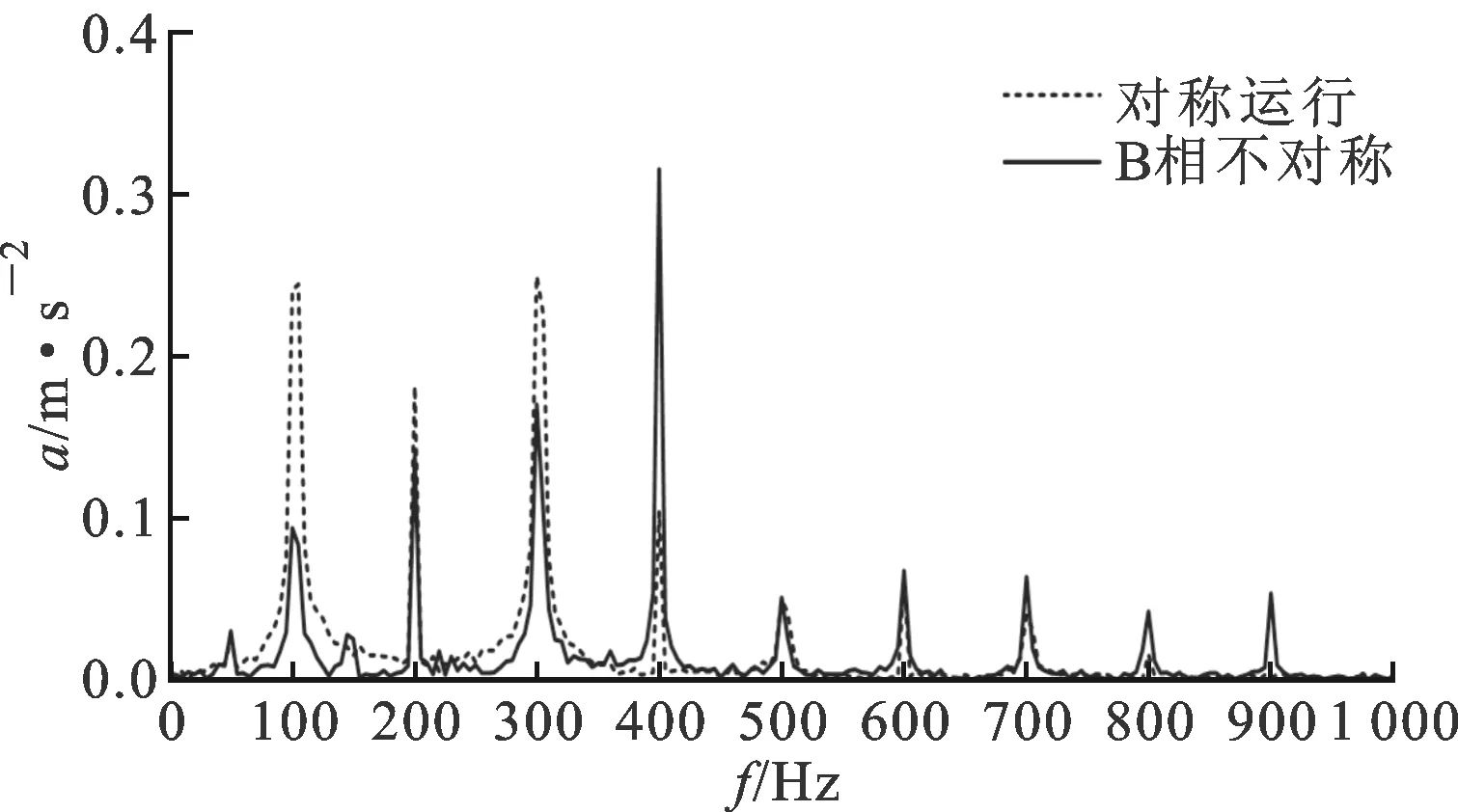
(a)A相

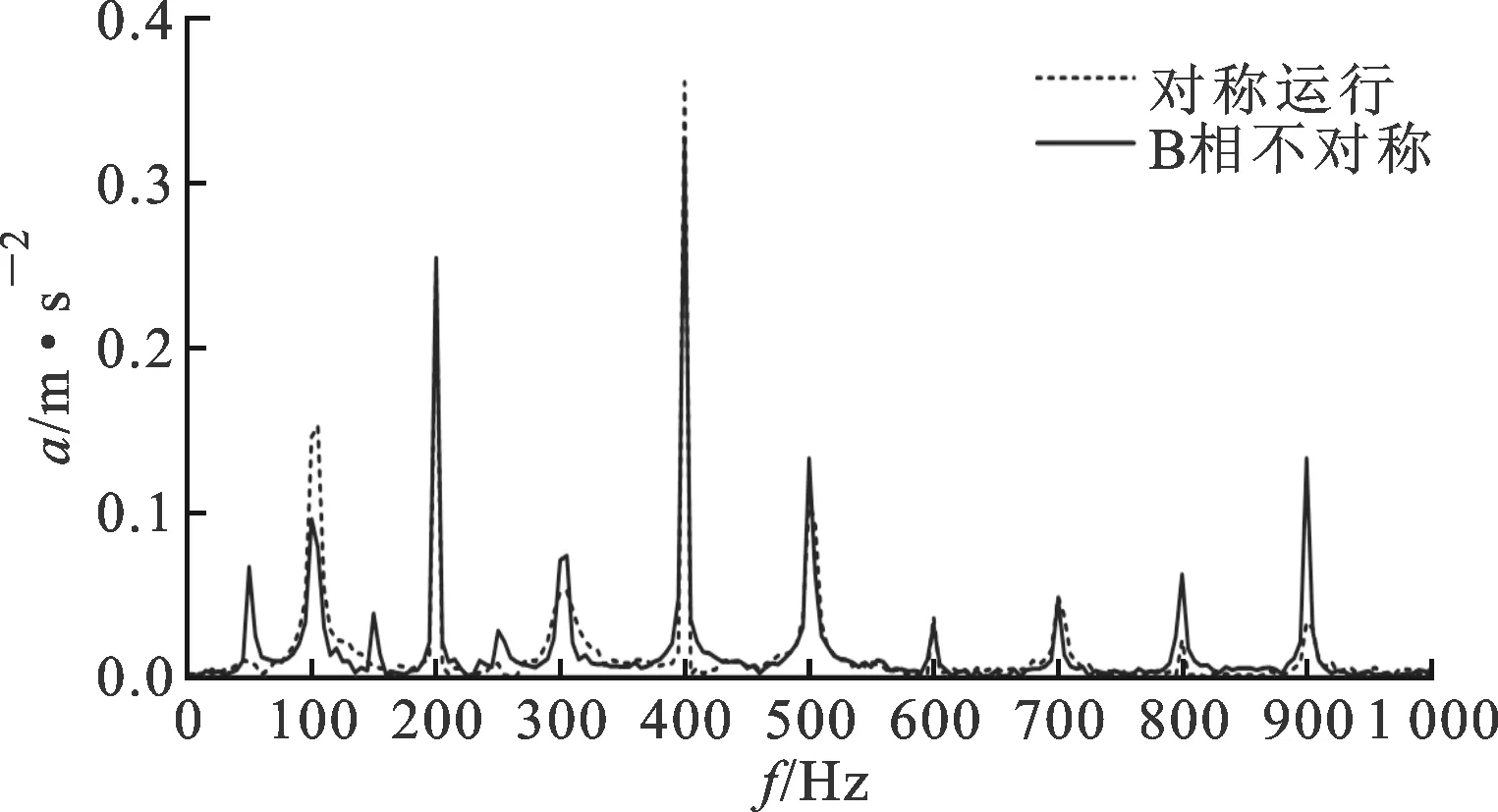
(b)B相

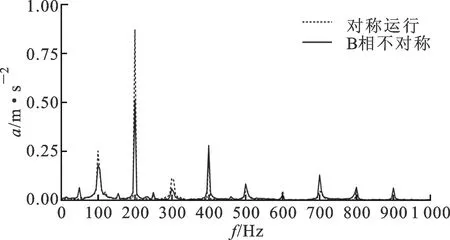
(c)C相图16 B相30%不平衡度运行对振动特性的影响

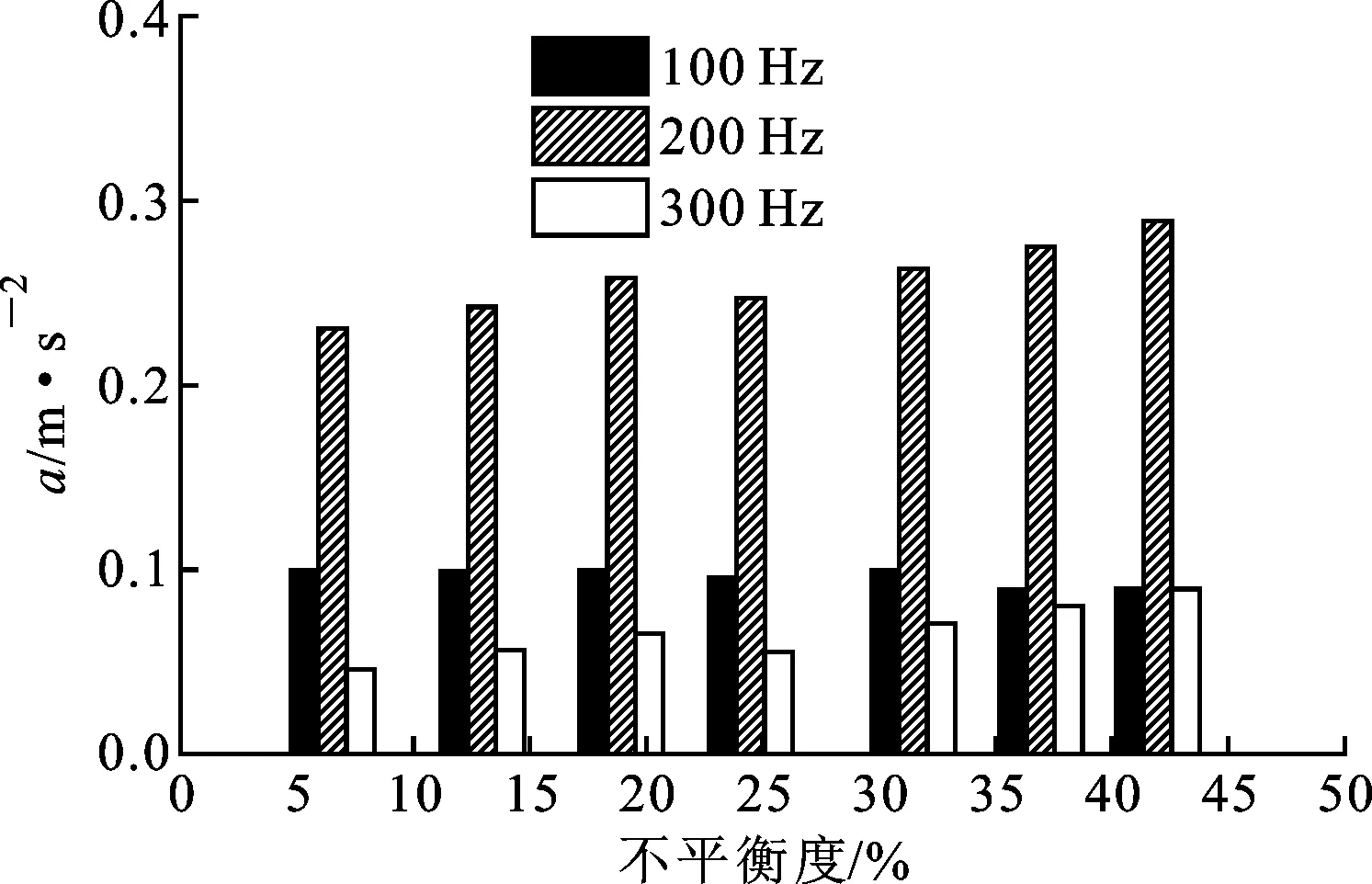
图17 三相不平衡度对不对称相振幅的影响

试验中,A、C相施加37%的负载电流水平,当试验变压器三相不平衡度达到40%时,不对称相(B相)基频振动加速度级变化为1 dB,200和300 Hz的振幅变化可达2～3 dB。国家标准明确规定,在正常情况下电网各相不平衡度不超过2%,短时不超过4%,接于公共连接点的每个用户引起该点不平衡值为1.6%,短时不超过2.6%[24],因此在变压器正常运行时,三相不平衡度对其振动幅值影响不大。当系统因故障出现三相不对称运行时,变压器振动频谱的变化出现50、150及250 Hz特征分量,不对称相振幅变化趋势与正常运行相不同,可作为故障特征加以区分。

2.2.5 油温的影响 油浸式电力变压器运行过程中,连续额定容量下的温升限值如表2所示[25]。由于变压器内部工作环境复杂,因此运行过程中油温变化较大,最高可达140 ℃,随着近年来超特高压的发展,在大容量、高电压的变压器上,温升效应更为显著。油温的变化对变压器振动的影响主要表现为对绕组及铁心力学特性的影响以及振动传递特性的影响。

表2 油浸式变压器连续额定容量下温升限值

对于一台220 kV电压等级200 MV·A容量的油浸式三相变压器进行温升试验下的振动特性测试,试验结果见图18。该台变压器的冷却方式是强迫导向油循环风冷(ODAF),油箱表面基频分量随油温上升呈现增长趋势,且同一绕组中部和底端的增长趋势基本一致(近似直线斜率接近)。当油温为48 ℃时开启风扇制冷系统,绕组底部振动信号出现小幅下降。值得一提的是,靠近C相绕组的风扇组开启后,A相振动信号中出现150 Hz左右的振动信号,视为风扇组对振动测试的干扰。为了验证变压器振动特性随油温变化规律的普遍性,另对一台强迫导向油循环风冷却的330 kV/240 MV·A的三相变压器以及一台油浸自冷式冷却的10 kV/50 kV·A的三相模型变压器进行了温升试验,对3台变压器各测试点振动随温度变化趋势拟合,得到各点斜率如表3所示。由表3可得,对于不同容量变压器不同测点处的振动信号,基频幅值随温度变化的直线斜率与变压器容量关系不大,取值范围在0.005～0.035 m/(s2·℃)内,同一绕组不同位置测点处的斜率值近似。

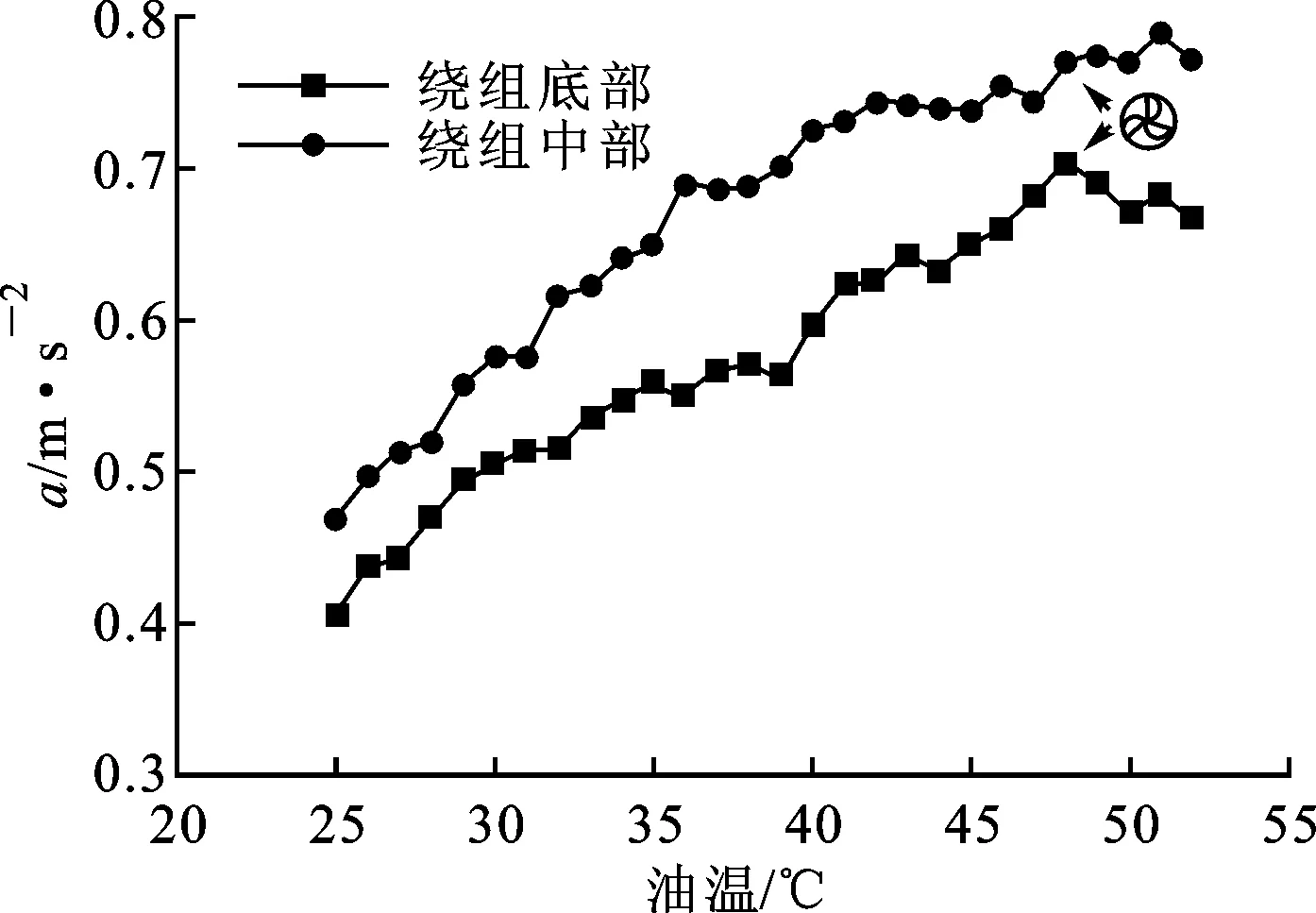
(a)A相测点基频振幅

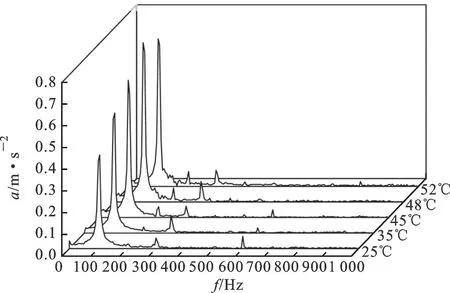
(b)A相底部振动频谱图18 油温对振动特性的影响

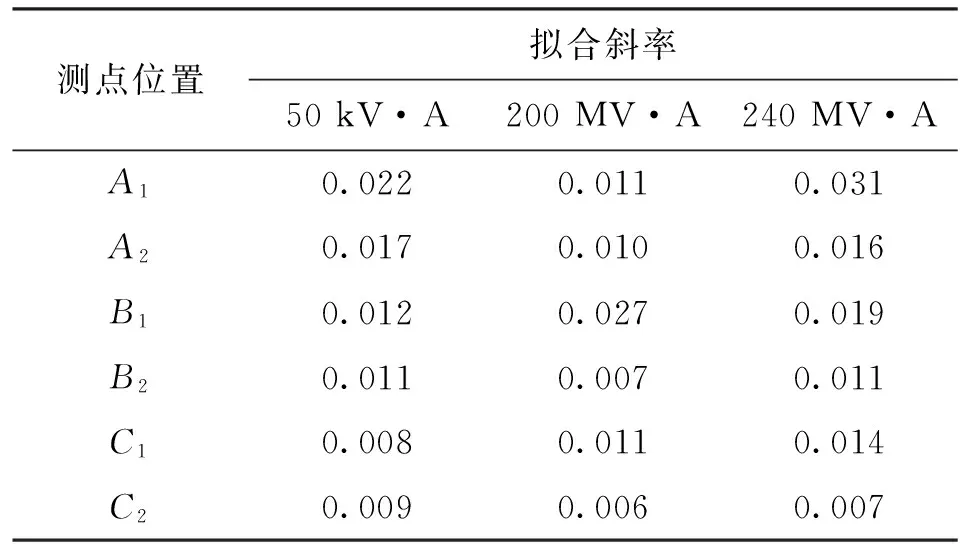
测点位置拟合斜率50kV·A200MV·A240MV·AA10.0220.0110.031A20.0170.0100.016B10.0120.0270.019B20.0110.0070.011C10.0080.0110.014C20.0090.0060.007

3 结 论

(1)针对不同分接条件下变压器振动特性试验,得到最大分接时的基频振动分量大于额定分接时的基频振动分量。

(2)通过理论分析及试验研究证实了变压器绕组及铁心产生的振动无法线性叠加,合成过程与变压器负载功率因数密切相关。变压器箱体振动信号中基频分量随功率因数的增大而增加,而由负载电流产生的漏磁场对铁心磁通存在抑制作用。

(3)三相不对称运行条件下变压器振动信号频谱中出现工频及150和250 Hz分量,为系统不对称运行时的零序电流谐波入侵的结果。不对称相上产生的严重过电压使铁心的谐振频率(一般为200、300 Hz处)振幅增加。

(4)通过试验得到了变压器绝缘垫块在不同温度下的力学特性,并以此为基础从理论上分析了油温变化对变压器振动的影响。在ODAF以及油浸自冷式冷却方式下,测试得到不同容量的变压器箱体表面不同位置的振动信号在20～50 ℃的温度区间内与油温的变化呈近似线性关系,拟合斜率在0.005～0.035 m/(s2·℃)范围内。

(5)确定了变压器测试时传感器的安装位置对振动信号的影响,通过试验证明了传感器安装位置偏差在±3 cm以上时振动信号已有极大变化,并探讨了变压器的风扇系统的开启对附近箱体振动信号的污染,建议带电测试时尽量避开风扇组。

[1]凌愍, 古正香.1990-1994年全国变压器事故统计及分析 [J].电网技术, 1996, 20(9): 47-52.LING Min, GU Zhengxiang.Nation-wide fault statistics and analysis of transformers from 1990 to 1994 [J].Power System Technology, 1996, 20(9): 47-52.

[2]王梦云.110 kV及以上变压器事故统计分析 [J].供用电, 2006, 23(1): 1-4.WANG Mengyun.Nation-wide fault statistics and analysis of 110 kV transformers [J].Distribution & Utilization, 2006, 23(1): 1-4.

[3]SOKOLOV V.Effective methods of assessment of insulation system conditions in power transformers: a view based on practical experience [C]∥Proceeding of the 1999 CIGRE Regional Meeting.Paris, France: CIGRE, 1999: 659-667.

[4]LAVALLE J C.Failure detection in transformer using vibrational analysis [D].Cambridge, MA, USA: MIT, 1986.

[5]汲胜昌, 刘味果, 单平, 等.变压器铁心及绕组状况的振动测试系统 [J].高电压技术, 2000, 26(6): 1-3.

JI Shengchang, LIU Weiguo, SHAN Ping, et al.The vibration measuring system for monitoring core and winding condition of power transformer [J].High Voltage Engineering, 2000, 26(6): 1-3.

[6]BARTOLETTU C, DESIDERIO M, FAZIO G, et al.Vibro-acoustic techniques to diagnose power transformers [J].IEEE Transactions on Power Delivery, 2004, 19(1): 221-229.

[7]王世山, 汲胜昌, 李彦明.利用振动法进行变压器在线监测的应用研究 [J].变压器, 2002, 39(1): 73-76.WANG Shishan, JI Shengchang, LI Yanming.Application research on transformer on-line monitoring with vibration method [J].Transformer, 2002, 39(1): 73-76.

[8]王璋奇, 王孟.电力变压器绕组轴向振动稳定性分析 [J].中国电机工程学报, 2002, 22(7): 24-28.

WANG Zhangqi, WANG Meng.Stability of axial vibration of power transformer windings [J].Proceedings of the CSEE, 2002, 22(7): 24-28.

[9]汲胜昌, 王俊德, 李彦明.稳态条件下变压器绕组轴向振动特性研究 [J].电工电能新技术, 2006, 25(1): 35-38.

JI Shengchang, WANG Junde, LI Yanming.Research on stability of axial vibration of power transformer windings in steady-state operation condition [J].Advanced Technology of Electrical Engineering and Energy, 2006, 25(1): 35-38.

[10]WEISER B, PFUTZNER H.Relevance of magnetostriction and force for the generation of audible noise of transformer cores [J].IEEE Transactions on Magnetics, 2000, 36(5): 3759-3777.

[11]祝丽花, 杨庆新, 闫荣格, 等.考虑磁致伸缩效应电力变压器振动噪声的研究 [J].电工技术学报, 2013, 28(4): 1-6.

ZHU Lihua, YANG Qingxin, YAN Rongge, et al.Research on vibration and noise of power transformer cores including magnetostriction effects [J].Transactions of China Electrotechnical Society, 2013, 28(4): 1-6.

[13]BELÉN G, JUAN C B,NGEL M A.Transformer tank vibration modelling as a method of detecting winding deformations: part II experimental verification [J].IEEE Transactions on Power Delivery, 2006, 21(1): 164-169.

[14]汲胜昌, 李彦明, 傅晨钊, 等.负载电流法在基于振动信号分析法监测变压器铁心状况中的的应用 [J].中国电机工程学报, 2003, 23(6): 154-158.

JI Shengchang, LI Yanming, FU Chenzhao, et al.Application of on-load current method in monitoring the condition of transformer’s core based on the vibration analysis method [J].Proceedings of the CSEE, 2003, 23(6): 154-158.

[15]郭俊, 汲胜昌, 沈淇, 等.盲源分离技术在振动法检测变压器故障中的应用 [J].电工技术学报, 2012, 27(10): 68-78.

GUO Jun, JI Shengchang, SHEN Qi, et al.Blind source separation technology for the detection of transformer fault based on vibration method [J].Transactions of China Electrotechnical Society, 2012, 27(10): 68-78.

[16]汲胜昌, 刘味果, 单平, 等.小波包分析在振动法监测变压器铁芯及绕组状况中的应用 [J].中国电机工程学报, 2001, 21(12): 24-27.

JI Shengchang, LIU Weiguo, SHAN Ping, et al.The application of the wavelet packet to the monitoring of the core and winding condition of transformers [J].Proceedings of the CSEE, 2001, 21(12): 24-27.

[17]JI Shengchang, LUO Yongfen, LI Yanming.Research on extraction technique of transformer core fundamental frequency vibration based on OLCM [J].IEEE Transactions on Power Delivery, 2006, 21(4): 1981-1988.

[18]董志刚.变压器的噪声(2) [J].变压器, 1995(10):31.

[19]HYVARINEN A, KARHUNEN J, QIA E.Independent component analysis [M].New York, USA: John Wiley & Sons Inc., 2001: 96-128.

[20]赵静月, 张庆, 康运和, 等.变压器制造工艺 [M].北京: 中国电力出版社, 2009: 237-241.

[21]诺顿 M P.工程噪声和振动分析基础 [M].盛元生, 等译.北京: 航空工业出版社, 1993: 158-160.

[22]曹建安, 裴云庆, 王兆安.基于零序谐波电流注入的三相功率因数校正技术研究 [J].中国电机工程学报, 2006, 26(16): 92-96.

CAO Jianan, PEI Yunqing, WANG Zhao’an.Research of 3 phase PFC technology based on injecting zero order [J].Proceedings of the CSEE, 2006, 26(16): 92-96.

[23]RAO S S.机械振动 [M].李欣业, 张明路, 译.北京: 清华大学出版社, 2009: 94-100.

[24]中国国家标准化管理委员会.GB/T 15543-2008 电能质量三相电压允许不平衡度 [S].北京: 中国标准出版社, 1996.

[25]国家质检总局.GB1094.2-1996 电力变压器:第2部分 温升 [S].北 京: 中国标准出版社, 1996.

(编辑 杜秀杰)

Vibration Mechanism and Influence Factors in Power Transformers

ZHU Yeye1, JI Shengchang1, ZHANG Fan1, LIU Yong1, DONG Hongkui2,CUI Zhigang2, WU Jiawei1

(1.State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University, Xi’an 710049, China;2.Yunnan Power Technology Branch, Yunnan Power Grid Corporation, Kunming 650000, China)

For an oil-immersed transformer core and pancake windings, the transformer vibration parameters are sought out and the vibration superposition is analyzed.The vibration monitoring system with piezoelectric vibration acceleration sensors is constructed and a series of experiments for the influence factors of the transformer vibration, such as current, power factor, unbalance factor and oil temperature, are conducted to investigate the vibration characteristics under different working conditions.It is found that the fundamental component of transformer tank under the greatest tapping is higher than that under principal tapping, transformer tank does not vibrate at linear superposition frequencies of core and windings; the fundamental component of transformer tank grows with the power factor; frequency components of 50 Hz, 150 Hz and 250 Hz appear in the vibration signals of power transformer due to the asymmetry.The experiments show that the fundamental component of the transformer vibration signal increases linearly with the oil temperature; temperature coefficient stays within 0.005-0.035 and does not depend upon the transformer capacity.

oil-immersed transformer; pancake windings; vibration; power factor; unbalance factor; oil temperature rise

2014-07-24。 作者简介:朱叶叶(1991—),女,硕士生;汲胜昌(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51377130)。

时间:2015-03-18

http:∥www.cnki.net/kcms/detail/61.1069.T.20150318.0940.002.html

10.7652/xjtuxb201506019

TM835.4

A

0253-987X(2015)06-0115-11