软件定义网络中应用二值粒子群优化的控制器部署策略

王丽霞,曲桦,赵季红,2,王力

(1.西安交通大学电子与信息工程学院,710049,西安;2.西安邮电学院通信工程系,710061,西安)



软件定义网络中应用二值粒子群优化的控制器部署策略

王丽霞1,曲桦1,赵季红1,2,王力1

(1.西安交通大学电子与信息工程学院,710049,西安;2.西安邮电学院通信工程系,710061,西安)

为了确定控制器的最优化部署方案,构建软件定义网络中逻辑上集中、物理上分布的控制平面,提出软件定义网络中应用二值粒子群优化的控制器部署策略。对控制器部署问题建模,以交换机到控制器的平均时延最短以及在网络中部署的控制器数量较少为多优化目标。提出粒子重构机制,实现粒子群优化算法的二值化,用以表示控制器在网络中部署的位置。基于二值粒子群优化算法设计多优化目标的控制器部署策略,仿真得到控制器部署问题的非劣最优解集合,对应给定的控制器数量,得到平均时延最小的控制器部署方案。实验结果表明,应用二值粒子群优化的控制器部署策略联合考虑了控制器数量和交换机到控制器的平均时延,为实现控制器最优化部署提供了依据。

控制器部署;软件定义网络;二值粒子群优化;非劣最优解集合

软件定义网络(software defined network,SDN)把原有封闭体系解耦,将控制平面与转发平面分离,提供了一种可编程的网络实现,由控制器组成逻辑上集中的控制平面来管理和监督一些简单的转发设备[1-2],这样的网络重构简化了控制平面设计,提供了可扩展的网络接口及接近最优的路径选择,同时全局视图的网络资源管理便于统一、灵活、高效地网络管理和维护[3]。

集中式控制平面的可扩展性较差,大规模网络中其性能急剧下降。目前多采取逻辑上集中、物理上分布的控制平面部署形式[4],例如Onix[3]、HyperFlow[5]等,这些网络架构通过把多个转发设备划分到不同的控制域中,形成分布式的控制平面,这是未来大规模SDN网络部署的重要解决思路。对于给定的网络拓扑,控制器部署问题主要考虑控制器的数量和控制器部署位置两方面[6]。

国内外关于控制器部署现有的算法是围绕时延[6]、可靠性[7-9]等不同的优化指标来确定控制器的部署位置。文献[6]定义了平均时延和最坏情况时延两个指标,分析了Internet2网络上的控制器部署问题,得到了控制器的最优部署方案,并指出在多数网络拓扑下,增加控制器的数量可以让时延以接近线性的比例减小,但是文中并没有给出具体的算法。文献[7-9]定义有效路径为可靠性指标,应用贪婪算法得到接近最优的解决方案,但该方法是在给定控制器数量情况下计算其放置位置的,对于不熟悉的网络拓扑,并不能很容易地知道控制器数量。因此,本文应用二值粒子群优化的控制器部署策略,可以同时确定给定网络拓扑下控制器的数量及部署位置。

二值粒子群优化算法(binary particle swarm optimization, BPSO)是基于群体智能的全局随机启发式搜索算法,粒子跟踪局部最优和全局最优来更新位置,有收敛速度快、效率高、极易实现全局优化等优点。控制器部署问题解决的是一个NP-hard(non-deterministic polynomial hard)问题[6],多目标则可以提供非劣解集[10]。应用二值粒子群优化的控制器部署策略将每个粒子定义为一种控制器部署方案,以交换机到控制器的时延和需要的控制器数量为优化目标,应用多目标二值粒子群优化算法[11-12]迭代进化得到非劣最优解集,并依此确定控制器的数量及其最优部署方案。最后,在Internet2拓扑[13]下仿真验证该算法,提供可行部署方案。

1 控制器部署问题建模

对于给定的网络环境G(V,E),V是所有节点集合,节点总数为n,即|V|=n,E∈V×V为链路集合,边权重代表网络时延。控制器部署问题的优化目标是交换机到控制器的平均时延最小以及在网络中部署的控制器数量k较小[6],平均时延为

(1)

式中:d(v,s)表示节点v∈V到控制器s∈V的最短路径。本文的目标是寻找控制器的部署集合S′使得|S′|=k,k尽可能小时La最小。

对所有节点编号,{C}表示控制器集合,|C|=C,{S}表示交换机集合,|S|=n。假定控制器部署在交换机的位置,∀i∈{S},∀j∈{C},xij取0或1,1表示在交换机j所在位置上部署控制器,反之表示不部署。

BPSO算法将其粒子的每一维及粒子局部最优、全局最优限制为1或0,速度不作限制。定义每个粒子Xi=[xi1,xi2,…,xij,…,xi,n]为一种控制器部署方案,其中i为粒子标号,j表示交换机标号。假设每个交换机的位置只能部署一个控制器,每个控制器至少控制一个交换机。控制器部署问题的优化目标是

min(f1(Xi),f2(Xi))

(2)

(3)

(4)

式中:f1(Xi)表示控制器的总数;f2(Xi)为节点到控制器的平均时延;

dj,i=d(j,i)

(5)

(6)

qmax≜ha(i,j)/f1(Xi)

(7)

其中qmax的值为控制器到交换机的平均跳数,为约数,lq表示第q跳的物理链路,ha为网络中所有节点对距离的平均跳数。

控制器部署问题的约束条件为

xij={0,1}

(8)

1≤f1(Xi)≤n

(9)

f2(Xi)≥0

(10)

(11)

式(8)表示xij取0或1;式(9)表示控制器数量在1到总节点数之间,即至少有一个控制器组成控制平面保证网络能够正常运行,但是不会每个节点都部署一个控制器;式(10)表示交换机到控制器的时延大于0;式(11)表示任意一个节点只有两种状态,有和没有控制器。

定理1 当网络中部署的控制器数与交换机数相等时,交换机到控制器的平均时延为0。

证明 ∀i,j,j=i时,dj,i=d(j,i)=0

定理2 当网络中部署的控制器数为1时,交换机到控制器的平均时延最大。

式中:ha(i,j)恒定,qmax≜ha(i,j)/f1(X)取最大值。

2 基于多目标BPSO算法控制器部署策略

2.1 基于多目标BPSO算法建模

粒子群优化算法(particle swarm optimization,PSO)是一种基于群体智能的全局随机启发式搜索算法[13],粒子跟踪局部最优和全局最优来更新位置。BPSO算法将粒子的每一维及粒子的历史最优、全局最优限制为1或0,速度不作限制[14-15]。在一个|S|=n维N个粒子的目标搜索空间中,第i个粒子的位置和速度表示为n维的向量,分别为Xi=xi1,xi2,…,xin),Vi=(vi1,vi2,…,vin,i=1,2,…,n)。进化中,粒子跟踪局部最优和全局最优来更新自己,分别记pbest=(pi1,pi2,…,pin),gbest=(pg1,pg2,…,pgn),i=1,2,…,n,如式(12)、(13)所示,式(14)是速度归一化取值方式

(12)

ω=ωmax-((ωmax-ωmin)/tmax)t

(13)

(14)

式(12)为粒子i的第j维速度更新方程;t为第t次迭代,惯性权重ω依据式(13)变化,ωmax=0.9,ωmin=0.4,c1=c2=2;r1和r2为[0,1]范围内的随机数。BPSO粒子位置更新方式如下。

do{[vmax,j]=max(v);vj=0;

}while(k≤n(C))

2.2 基于多目标BPSO算法的控制器部署策略

应用多目标的二值粒子群优化算法,适应度函数为

F=min(f1(Xi),f2(Xi))

(15)

基于多目标BPSO算法的控制器部署策略步骤如下。

步骤1 限定粒子群的位置以及速度范围,设定种群规模N,粒子最大进化次数tmax,控制器数量n(C);

步骤3 根据式(15)计算初始时刻粒子的适应度函数F;

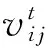
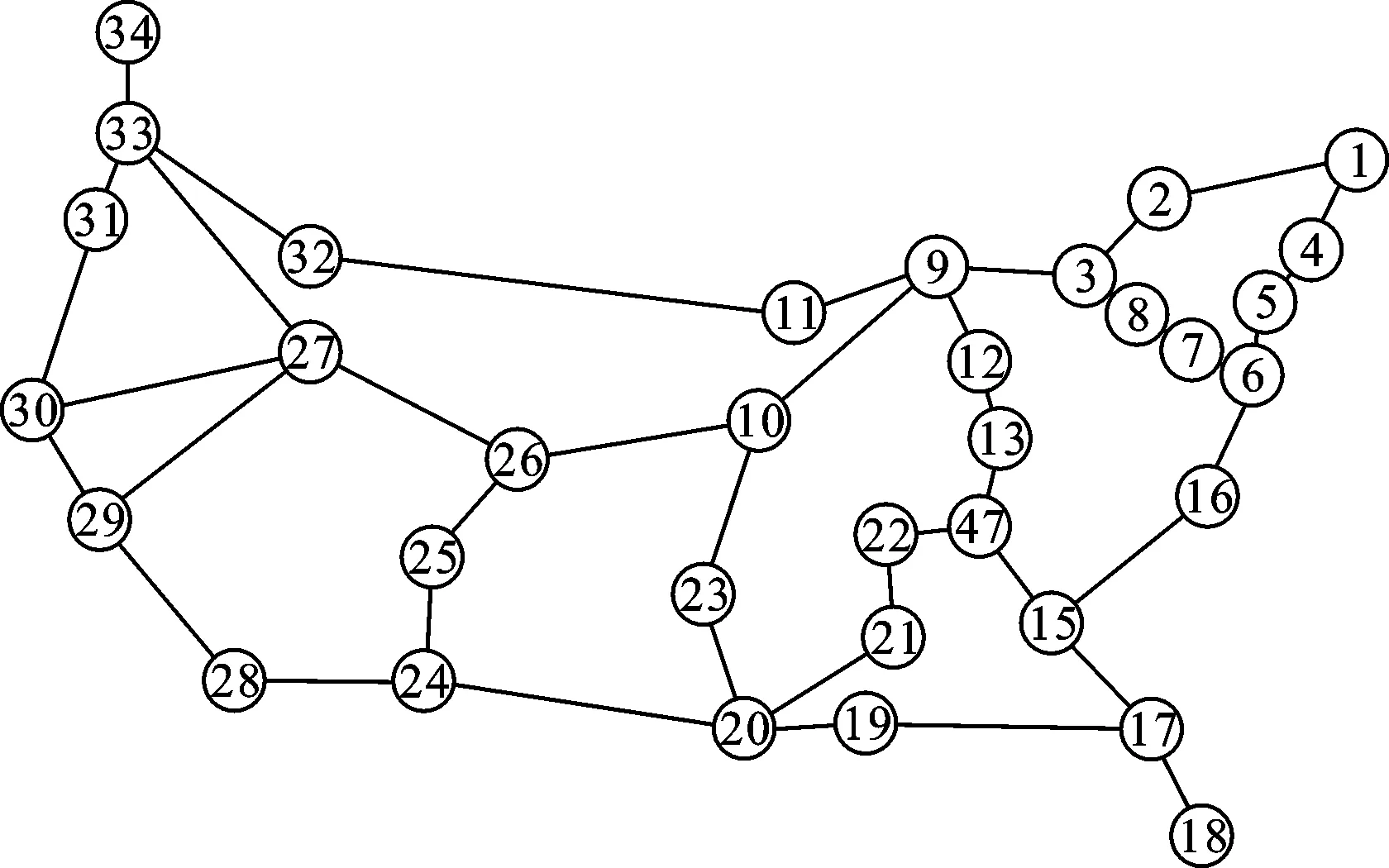
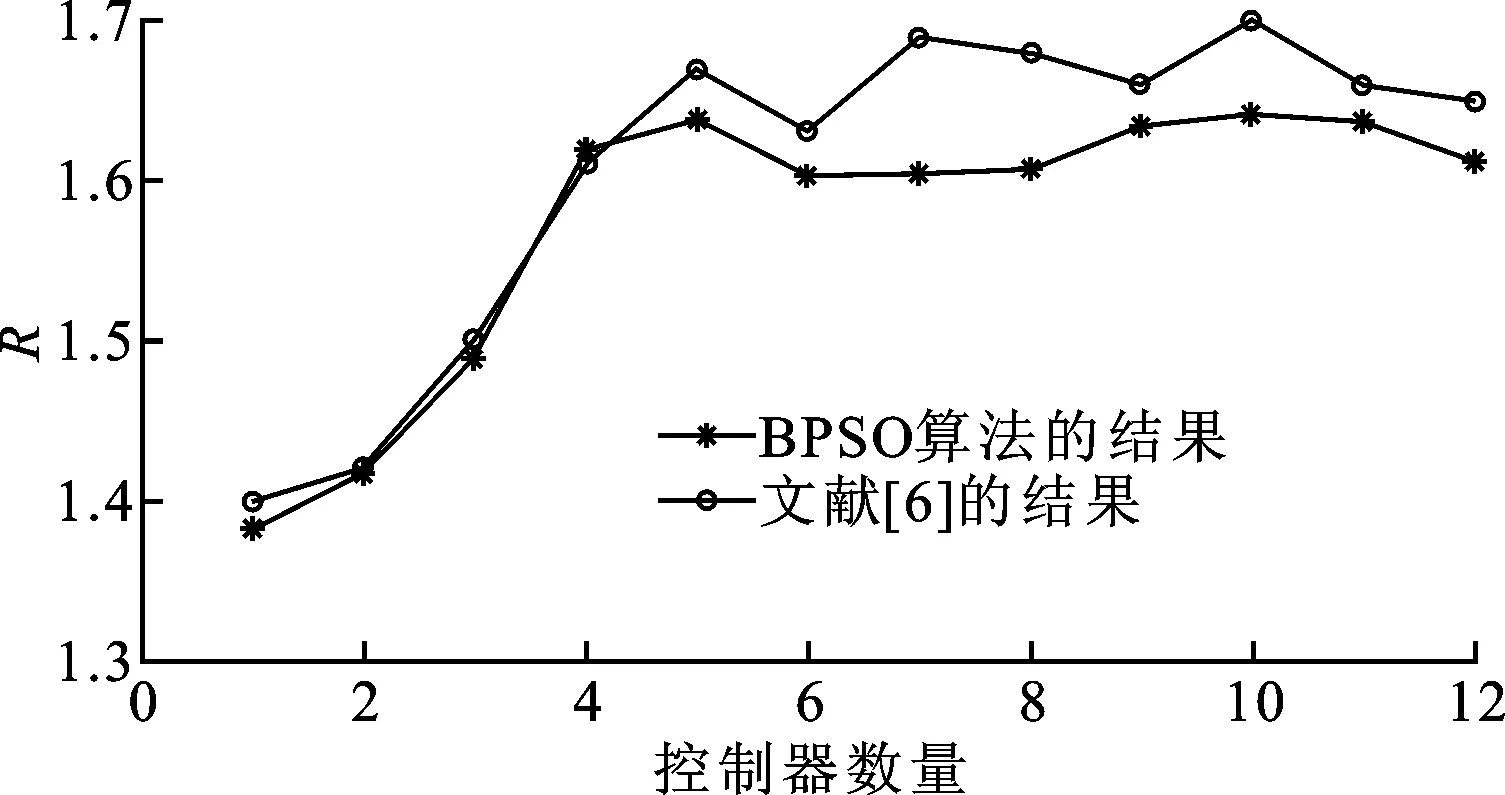
步骤5 所有粒子维数处理完毕,判断t

步骤6 判断迭代次数t

步骤7 判断k

步骤8 得到最终的非劣最优解集,分析判断选取最优的k值和部署情况。

3 仿真结果

3.1 仿真环境配置

为了验证算法的有效性,我们采用34节点的Internet2网络拓扑[13],对每个节点标号,用距离表示时延,单位为km,如图1所示;假设每个节点放置交换机,而控制器部署在交换机的位置上。实验仿真中,设置粒子数量为20,最大迭代次数为1 000。

图1 Internet2网络拓扑

3.2 Pareto解集

仿真得到了控制器数量从1～34变化的控制器部署方案,表1显示了控制器数量为1～12的最优部署方案和较优时延值,为管理员部署控制器提供了参考。随着控制器数量的增加时延减小。控制器数量为1时时延最大,而控制器数量为34,即每个节点均部署控制器时,控制器时延最小为0。

表1 控制器数量为1～12的部署方案

3.3 增加控制器数量的效率

为了验证本文算法的有效性,仿真结果与文献[6]给出的Internet2环境下的部署结果比较如图2、3所示,结果显示本文算法能够有效地解决控制器部署问题。

图2显示了随机平均时延与优化之后的最优时延的比值,设为R,随着控制器数量的变化,表现了某个控制器数量环境下,算法优化部署的效益性。该值越大,表示优化时延相对随机平均时延越小,即效益越好。例如控制器数量为4时,应用本文算法所得最优时延为1 108.16 km,见表1,随机平均时延为1 794.24 km(由最短路径所得的随机部署时延值),随机平均时延与最优时延之比约为1.6,同理得控制器数量为3时比例约为1.49,说明控制器数量为4时比控制器数量为3时得到了更大的时延优化比值、更优的部署效益。由图2可见,控制器数量为4时,随机平均时延与最优时延之比最大,说明控制器数量为4时,部署效益最好。

图2 随机平均时延与最优时延之比随控制器数量的变化

图3 控制器数量为1～12时的收益比

3.4 算法收敛性

图4 不同控制器数量下时延随迭代次数的变化

图4表示控制器数量分别为5、10、17时应用二值粒子群优化的控制器部署算法的收敛性。该算法可以得到任意控制器数量情况下的控制器部署方案和收敛值。由图可见,随着控制器数量增加,算法收敛时间变长,速度变慢。这是因为控制器数量增加,控制器部署可能方案数量增加,收敛到较优方案的时间增加。

4 结 论

本文提出软件定义网络中应用二值粒子群优化的控制器部署策略,在满足网络性能和预算的条件下,为给定的网络拓扑部署多少个控制器以及如何部署提供了可行的方案。该策略以控制器数量和控制器到交换机的平均时延为优化目标,要求在控制器数量尽可能少的情况下平均时延最小,应用二值离散粒子群算法迭代进化,得到了最终的非劣最优解集,并以此确定出控制器的数量和部署方案。

[1]MENDONCA M, ASTUTO B N, NGUYEN X N, et al.A survey of software-defined networking: past, present, and future of programmable networks [J].IEEE Communications Surveys and Tutorials, 2014, 16(3): 1617-1634.

[2]Open Networking Foundation.Software-defined networking definition[EB/OL].(2013-05-01)[2014-05-12].http:∥www.openflowswitch.org.

[3]KOPONEN T, CASADO M, GUDE N, et al.Onix: a distributed control platform for large-scale production networks [C]∥Proceedings of the 9th USENIX Symposium on Operating Systems Design and Implementation.Berkeley, CA, USA: USENIX Association, 2010: 351-364.

[4]LEVIN D, WUNDSAM A, HELLER B, et al.Logically centralized?: state distribution trade-offs in software defined networks [C]∥Proceedings of the First Workshop on Hot Topics in Software Defined Networks.New York, USA: ACM, 2012: 1-6.

[5]LANTZ B, HELLER B, MCKEOWN N.A network in a laptop: rapid prototyping for software-defined networks [C]∥Proceedings of the 9th ACM Sigcomm Workshop on Hot Topics in Networks.New York, USA: ACM, 2010: 1-6.

[6]HELLER B, SHERWOOD R, MCKEOWN N.The controller placement problem [C]∥Proceedings of the First Workshop on Hot Topics in Software Defined Networks.New York, USA: ACM, 2012: 7-12.

[7]HU Yannan, WANG Wendong, GONG Xiangyang, et al.Reliability-aware controller placement for software-defined networks [C]∥Proceedings of the 2013 IFIP/IEEE International Symposium on Integrated Network Management.Piscataway, NJ, USA: IEEE, 2013: 672-675.

[8]BEHESHTI N, ZHANG Ying.Fast failover for control traffic in software-defined networks [C]∥Proceedings of the 2012 IEEE Global Communications Conference.Piscataway, NJ, USA: IEEE, 2012: 2665-2670.

[9]刘娟, 黄韬, 魏亮.SDN中基于可靠性优化的控制器放置算法研究[EB/OL].(2013-12-06)[2014-05-05].http:∥www.paper.edu.cn/releasepaper/content/201312-161.

[10]ZITZLER E, THIELE L.Multi-objective evolutionary algorithms: a comparative case study and the strength Pareto approach [J].IEEE Transactions on Evolutionary Computation, 1999, 3(4): 257-271.

[11]COELLO C A, LECHUGA M S.MOPSO: a proposal for multiple objective particle swarm optimization [C]∥Proceedings of the 2002 Congress on Evolutionary Computation.Piscataway, NJ, USA: IEEE, 2002: 1051-1056.

[12]MANTWAY A H, Al-MUHAINI M M.Multi-objective BPSO algorithm for distribution system expansion planning including distributed generation [C]∥Proceedings of the 2008 Transmission and Distribution Conference and Exposition.Piscataway, NJ, USA: IEEE, 2008: 1-8.

[13]Internet2 Open Science, Scholarship and Services Exchange.Internet2 network [EB/OL].(2013-06-04)[2014-06-21].http:∥www.internet2.edu/network/ose/.

[14]KENNEDY J, EBERHART R.Particle swarm optimization [C]∥Proceedings of the International Conference on Neural Networks.Piscataway, NJ, USA: IEEE, 1995: 1942-1948.

[15]KENNEDY J, EBERHART R C.A discrete binary version of the particle swarm algorithm [C]∥Proceedings of the 1997 Conference on Systems, Man and Cybernetics.Piscataway, NJ, USA: IEEE, 1997: 4101-4108.

(编辑 武红江)

A Strategy of Controller Placement in Software Defined Networks Using Binary Particle Swarm Optimization

WANG Lixia1, QU Hua1, ZHAO Jihong1,2, WANG Li1

(1.School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2.School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710061, China)

A strategy of controller placement in software defined networks using the binary particle swarm optimization is proposed to find the optimal placement scheme of controllers and to build a logically centralized and physically distributed control plan for the controller placement problem in SDN.An optimization model is built for the problem, and the optimization goals are to minimize both the number of controllers and the latency from controllers to switch.The binary particle reconstruction mechanism is put forward to denote the position of the controller in the network.A binary particle swarm algorithm is applied to find the set of Pareto optimum for the problem, from which a strategy of controller placement is provided.Simulation results show that the proposed algorithm gets the optimal placement strategies with minimum latency for different number of controllers.

controller placement problem; software defined network; binary particle swarm optimization; pareto set

2014-11-14。 作者简介:王丽霞(1989—),女,硕士生;曲桦(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61371087);国家高技术研究发展计划重大专项资助项目(2013ZX0302010-003);国家高技术研究发展计划资助项目(2014AA01A701,2014AA01A706,2014AA01A707)。

10.7652/xjtuxb201506011

TP391

A

0253-987X(2015)06-0067-05