永磁同步电机非奇异快速终端可变边界层滑模控制

常雪剑,刘凌,崔荣鑫

(1.西安交通大学电气工程学院,710049,西安;2.西北工业大学航海学院,710072,西安)



永磁同步电机非奇异快速终端可变边界层滑模控制

常雪剑1,刘凌1,崔荣鑫2

(1.西安交通大学电气工程学院,710049,西安;2.西北工业大学航海学院,710072,西安)

针对永磁同步电机(PMSM)调速系统易受到参数不确定性及负载扰动的影响,提出了一种新型可变边界层的非奇异快速终端滑模(NFTSM)控制策略。首先,构建可在有限时间内快速收敛的非奇异快速终端滑模面;然后,采用角速度与q轴定子参考电流的二阶模型设计速度环滑模控制器,减小了角速度与q轴定子参考电流一阶模型所引起的误差,并避免了终端滑模面奇异问题;最后,设计可变边界层使误差减小至阈值时系统状态切换至小边界层,实现抖振和跟踪精度的协调控制。数值仿真结果表明,NFTSM控制策略与传统PI控制策略相比,转速超调量小,响应速度快,稳态精度近似为0,对参数摄动和负载扰动鲁棒性强,且在有效削弱抖振的同时保证了转速的稳态精度。

永磁同步电机;滑模控制;二阶模型;负载扰动;参数摄动

永磁同步电机(permanent magnet synchronous motor, PMSM)因具有结构简单、高效率、高功率密度、高转矩电流比、低转动惯量等优点,被广泛应用于航空航天、数控机床、智能机器人等工业领域。由于PMSM是一个多变量、强耦合的非线性系统,且在运行过程中存在参数变化、负载扰动等不确定性干扰,传统的PI控制器依赖于电机的模型和参数,难以满足电机对调速系统日益增长的要求。近年来,一些基于智能控制的方法被应用于永磁同步电机,提高了系统的鲁棒性和动态性能[1-7]。

滑模控制因具有对PMSM系统参数时变和外部扰动的强鲁棒性,成为国内外学者研究的热点领域。滑模控制根据系统的当前状态(如误差及其各阶导数等)构成滑模面,通过控制量的切换,迫使系统沿着规定的状态轨迹作小幅度、高频率的滑动,使系统在受到参数摄动或外界干扰时具有不变性,且响应速度快,物理实现简单,可有效地应用于永磁同步电机的控制[8-9]。

目前,滑模控制所采用的滑模面主要有积分滑模、线性滑模、终端滑模(terminal sliding mode,TSM)、非奇异终端滑模 (nonsingular terminal sliding mode, NTSM)等。文献[10]采用积分滑模消除永磁同步电机调速系统的稳态误差,避免了对速度微分引起的高频噪声,但积分滑模在大的初始误差和干扰下容易产生积分饱和,导致超调量大。传统线性滑模的系统状态以指数形式渐进收敛,无法收敛至平衡点。文献[11]采用快速终端滑模抑制电力系统的混沌振荡,通过对线性滑模引入非线性项,提高了系统的收敛速度并使系统状态在有限的时间内收敛至平衡点,但对滑模面求导后,控制律中存在状态指数为负的项,可能会使控制量趋于无穷大,产生奇异点。文献[12]提出了一种基于非奇异终端滑模观测器的PMSM无传感器控制技术,提高了观测器的动态响应速度、控制精度及鲁棒性,避免了奇异问题。文献[13-14]通过理论和仿真分析证明当系统状态离平衡点较远时,非奇异终端滑模面由于误差收敛速度表达式的指数小于1,远低于线性滑模的收敛速度,动态性能较差。抖振问题一直是滑模控制的难点,目前所采用的削弱抖振的方法有准滑模法[15]、神经滑模法[16]、模糊滑模法[17]、干扰观测器法[18]等。其中准滑模控制容易实现,且能有效削弱抖振,但采用传统的固定边界层时,难以同时满足抖振和精度的要求,而其他方法均存在参数匹配难、响应延时、规则不易确定等问题。

为了提高系统状态离平衡点较远时的收敛速率,避免奇异现象,本文基于可变边界层通过加入误差状态的高次项,提出了一种应用于永磁同步电机调速系统的非奇异快速终端滑模(nonsingular fast terminal sliding mode, NFTSM)控制策略。为了获得更高性能的调速系统,采用角速度与q轴定子参考电流更为精确的二阶模型设计控制器,并设计Lyapunov函数证明了控制器的有效性。通过改变边界层的大小实现削弱抖振和提高控制精度的协调控制。

1 永磁同步电机(PMSM)数学建模

为了简化分析,首先对永磁同步电机(PMSM)系统进行建模。假设磁路不饱和,空间磁场呈正弦分布,不计铁芯磁滞损耗和涡流损耗,表贴式永磁同步电机在d-q两相旋转坐标系下的状态方程为

(1)

式中:ud、uq、id、iq分别是d轴、q轴的定子电压、电流;Rs为定子电阻;L为定子电感;ψf为转子磁链;np为极对数;ω为转子机械角速度;B为摩擦系数;J为转动惯量;TL为负载转矩。

2 非奇异快速终端滑模速度控制器设计

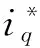
2.1 非奇异快速终端滑模面的设计

为了提高永磁同步电机转速的响应速度和跟踪精度,本文提出如下非奇异快速终端滑模面

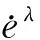
(2)

式中:e为误差变量;γ=g/h,λ=p/q,g、h、p、q为正奇数;1<λ<2,γ>λ;α、β为大于0的常数。令s=0,则误差收敛速度为

(3)

当系统状态离平衡点较远时,误差收敛速度由式(3)右端e的高次项αeγ/β起主要作用,收敛速度快;当系统状态靠近平衡点时,忽略e的高次项,收敛速度近似于非奇异终端滑模面。因此,在滑动阶段NFTSM控制较NTSM控制可实现全局快速收敛,且与TSM控制相比式(2)中状态指数皆大于1,避免了对s求导后,具有负指数的状态产生奇异性问题。

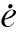
(4)

通过选取恰当的参数α、β、γ、λ,可使系统在有限时间内到达平衡态。

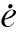
(5)

2.2 基于二阶模型的控制律求取

(6)

式中:d(t)=-Bω/J-TL/J为系统扰动量。

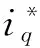
(7)

式中:S为复频率。

根据q轴电流环,可得

(8)

式中:uq(S)为q轴电流环的输出;Kp、Ki分别为q轴电流环PI调节器的比例、积分参数。

由式(8)得

(9)

将式(9)代入式(7)得

(10)

定义

(11)

为速度环滑模控制器的输出,则有

(12)

式(10)可简化为

(13)

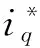
(14)

滑模控制器的设计中,控制律通常由等效控制ueq和切换控制usw组成。等效控制用以控制系统的确定部分,将系统状态保持在滑模面上,切换控制通过高频切换迫使系统状态在滑模面上运动趋于稳定点,实现对不确定性和外加干扰的鲁棒控制。

(15)

为使状态快速到达滑模面,减小抖振,设计切换控制为

(16)

式中:ε>0,η>0。

由上可得速度环滑模控制器的控制律为

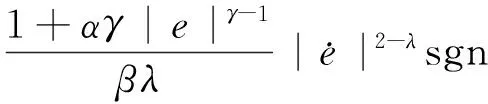
(17)

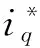
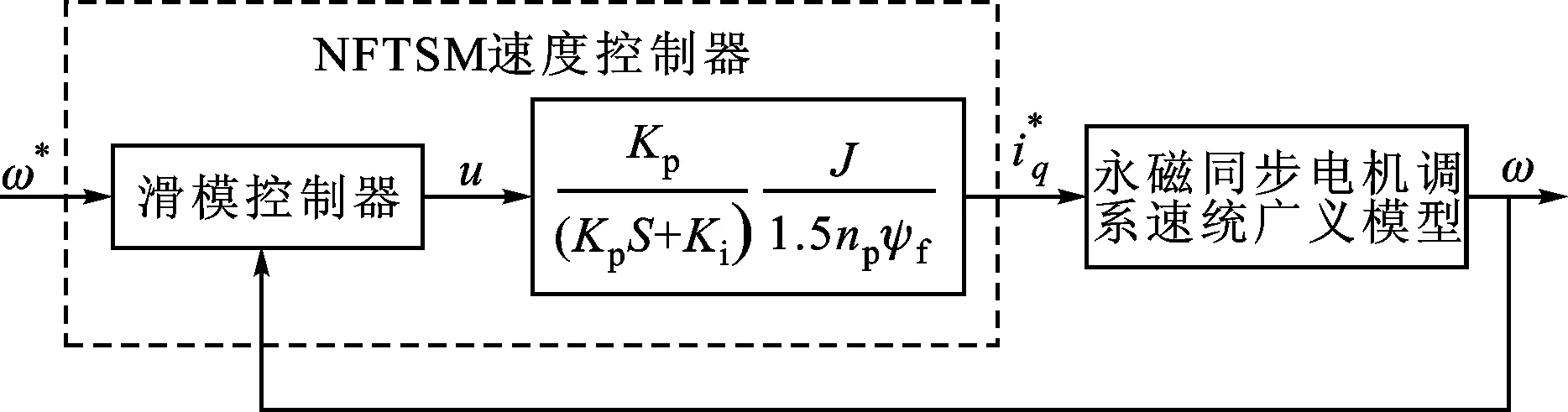
图1 基于永磁同步电机调速系统二阶模型的NFTSM控制系统简化框图

为保证系统在任意初始状态都能到达滑模态,定义Lyapunov函数为

(18)

假设D(t)有上界,且有|D(t)|≤ε,则

(19)

由此得证系统稳定。

2.3 边界层分析

由于系统存在惯性、延时、滞后开关等因素,使运动点到达滑模面后,由于开关函数的不连续性,在滑模面附近来回穿越,形成抖振。抖振不仅影响控制的精度,增大机械损耗,还会激发高频未建模动态,破坏系统性能,产生振荡甚至失稳,所以必须对抖振加以限制,但抖振是必须存在的,消除了抖振意味着消除了滑模控制抗扰动、抗摄动能力,所以只能在一定程度上削弱抖振。通常采用饱和函数sat(s)代替开关函数sgns来削弱抖振,即在边界层内采用连续的反馈控制,在边界层外采用正常的切换控制。饱和函数的表达式为

(20)

式中:δ>0,为边界层厚度。δ越小,控制精度越高,但控制增益增大,抖振增强;δ越大,抖振减小,但控制增益变小,响应速度减慢,超调量与稳态误差较大,控制效果差。为此,采用一种可变边界层准滑模策略,即系统状态先到达较大的边界层,当误差减小至一定值ec(ec>0)时,切换至小边界层,既削弱了抖振,也保证了跟踪精度。

可变边界层厚度表达式为

δ=γ1δ2+(1-γ1)δ1

(21)

式中:0<δ1<δ2;当|e|>ec时,γ1=1,当|e|≤ec时,γ1=0。另外,为了使转速曲线更为平滑,误差减小得更快,使|s|>δ20时,δ2=δ20,|s|≤δ20时,δ2=δ20exp(-kt),其中δ20为δ2的最大值,k为速率调节系数。通过选择适当的系数k>0,可实现边界层的平滑过渡。

3 仿真结果与分析

建立基于MATLAB/Simulink的系统仿真模型,采用id=0的矢量控制策略,实现永磁同步电机的解耦控制。系统的速度控制器设计为NFTSM滑模控制器,以实现转速的快速响应及强鲁棒性;d轴和q轴电流控制器设计为PI控制器,以保证电流内环的快速性。永磁同步电机调速系统拓扑图如图2所示。

图2 永磁同步电机调速系统拓扑图

NFTSM滑模控制器电机额定参数为:PN=3kW,UN=200V,IN=18A,nN=3 000r/min,Rs=0.258Ω,Ld=Lq=3.5mH,ψf=0.057Wb,B=0N·m·s,J=0.006 5kg·m2,np=5,q轴电流限幅值iqm=18A。

PI电流控制器参数为:Kp=6,Ki=1 800。

NFTSM速度控制器参数为:α=1×10-4,β=2×10-4,γ=1.5,λ=1.4,δ1=0.5,δ20=3,k=10,ec=0.2,ε=6×106,η=35×104。

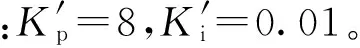
给定转速为600 r/min,在0.1 s时加入3 N·m负载的仿真结果如图3～图8所示。

由图3可得,在NFTSM控制作用下,电机转速在0.068 s时就进入稳态,而在NTSM控制作用下,转速于0.07 s进入稳态,可见NFTSM控制能够比NTSM控制更快地趋于给定转速。

由图4所示,NFTSM控制与PI控制相比,在启动阶段,PI控制使转速在给定值附近超调比NFTSM控制大,波动大,响应速度慢,但能趋于给定值。在0.1 s突增负载时,NFTSM控制能够使转速快速跟踪给定值,稳态精度近似为0,而PI控制降速后,只能稳定在599 r/min。

图3 NTSM控制与NFTSM控制的转速响应

图4 PI控制与NFTSM控制的转速响应

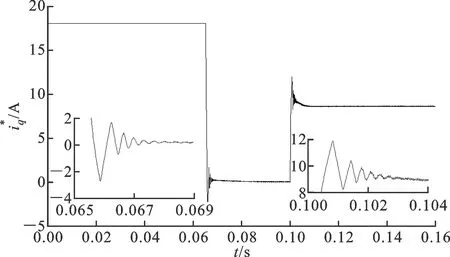
图5 小边界层下NFTSM控制的抖振图

图6 大边界层下NFTSM控制的抖振图

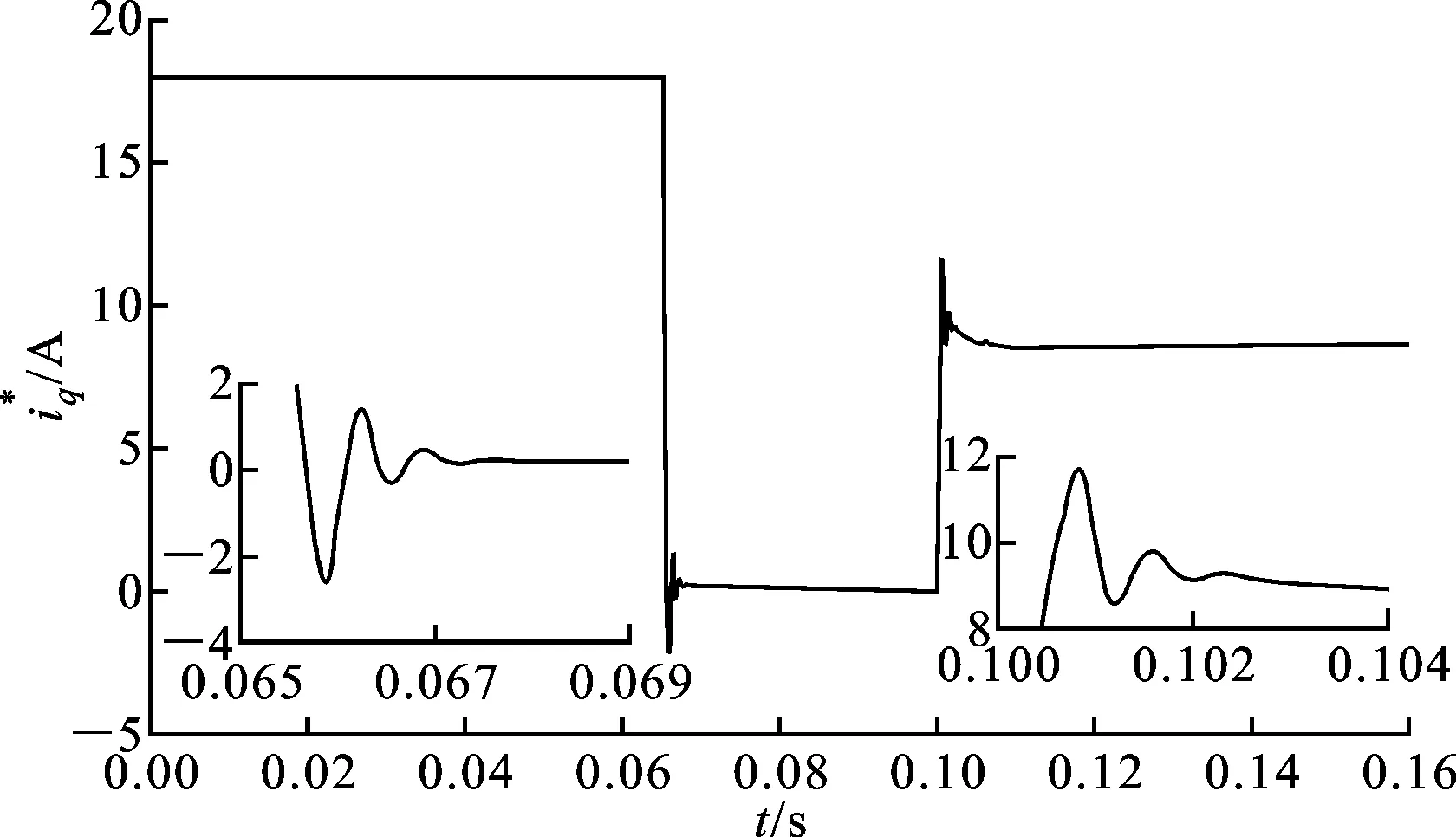
图7 可变边界层下NFTSM控制的抖振图

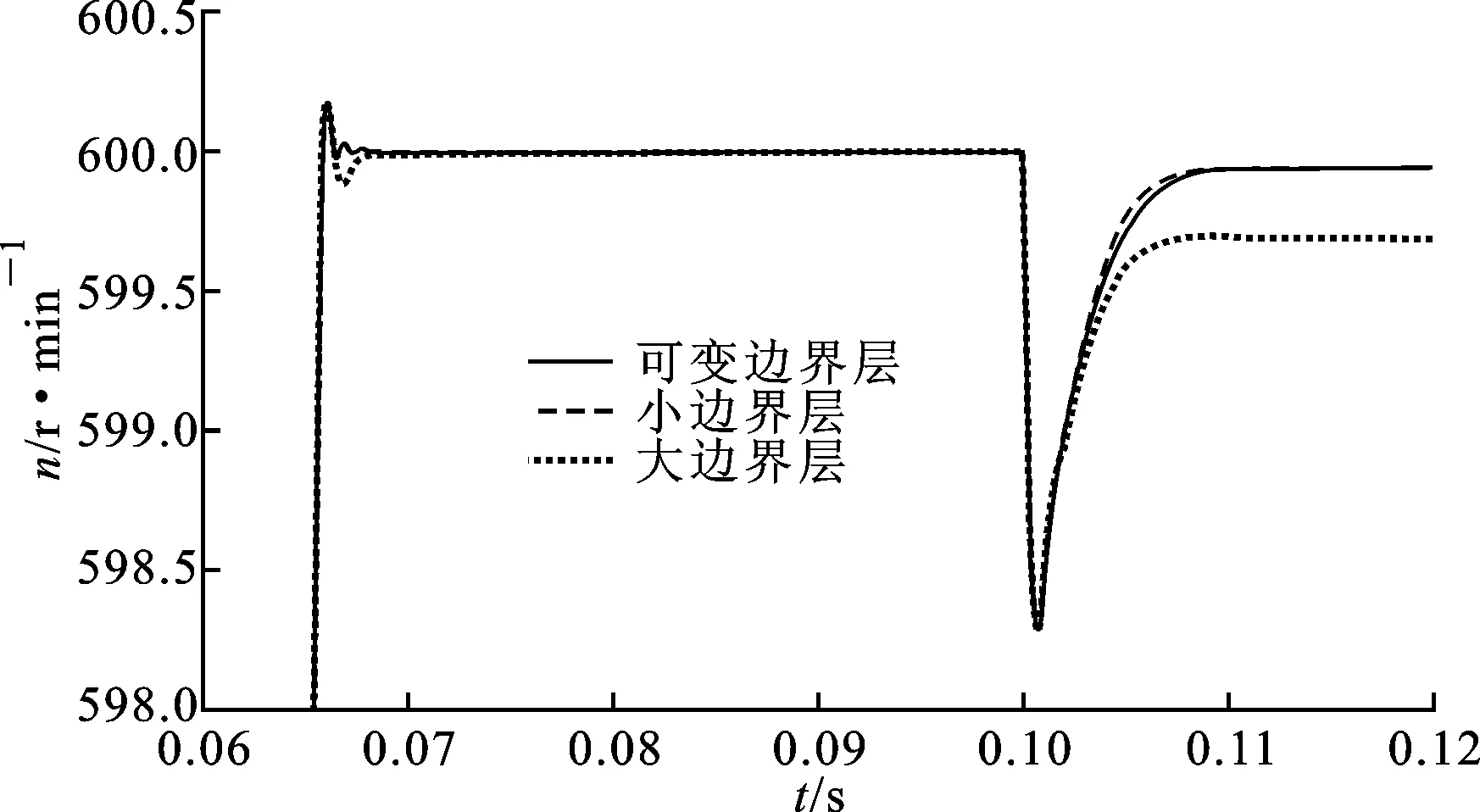
图8 不同边界层下NFTSM控制的转速响应

给定转速为600 r/min,在0.1 s时加入2 N·m负载,0.13 s时负载变为4 N·m,0.16 s时变为3 N·m,负载突变时PI控制与NFTSM控制结果对比如图9所示。给定转速为600 r/min,在0.14 s时加入3 N·m负载,转动惯量J发生变化时,NFTSM控制作用下仿真结果如图10所示;磁通ψf发生变化时,NFTSM控制作用下仿真结果如图11所示。

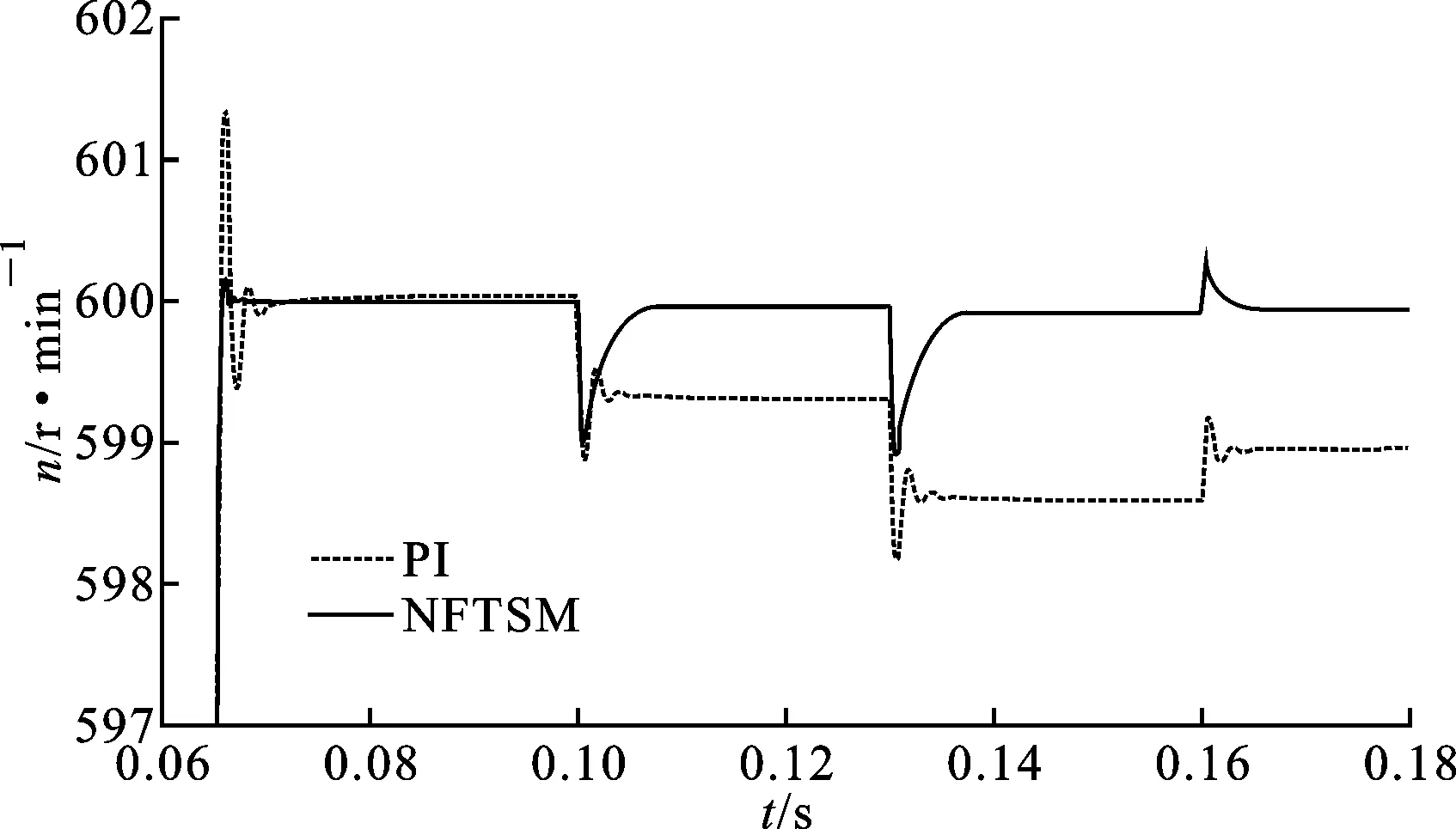
图9 不同时刻负载突变时PI控制与NFTSM控制的转速响应

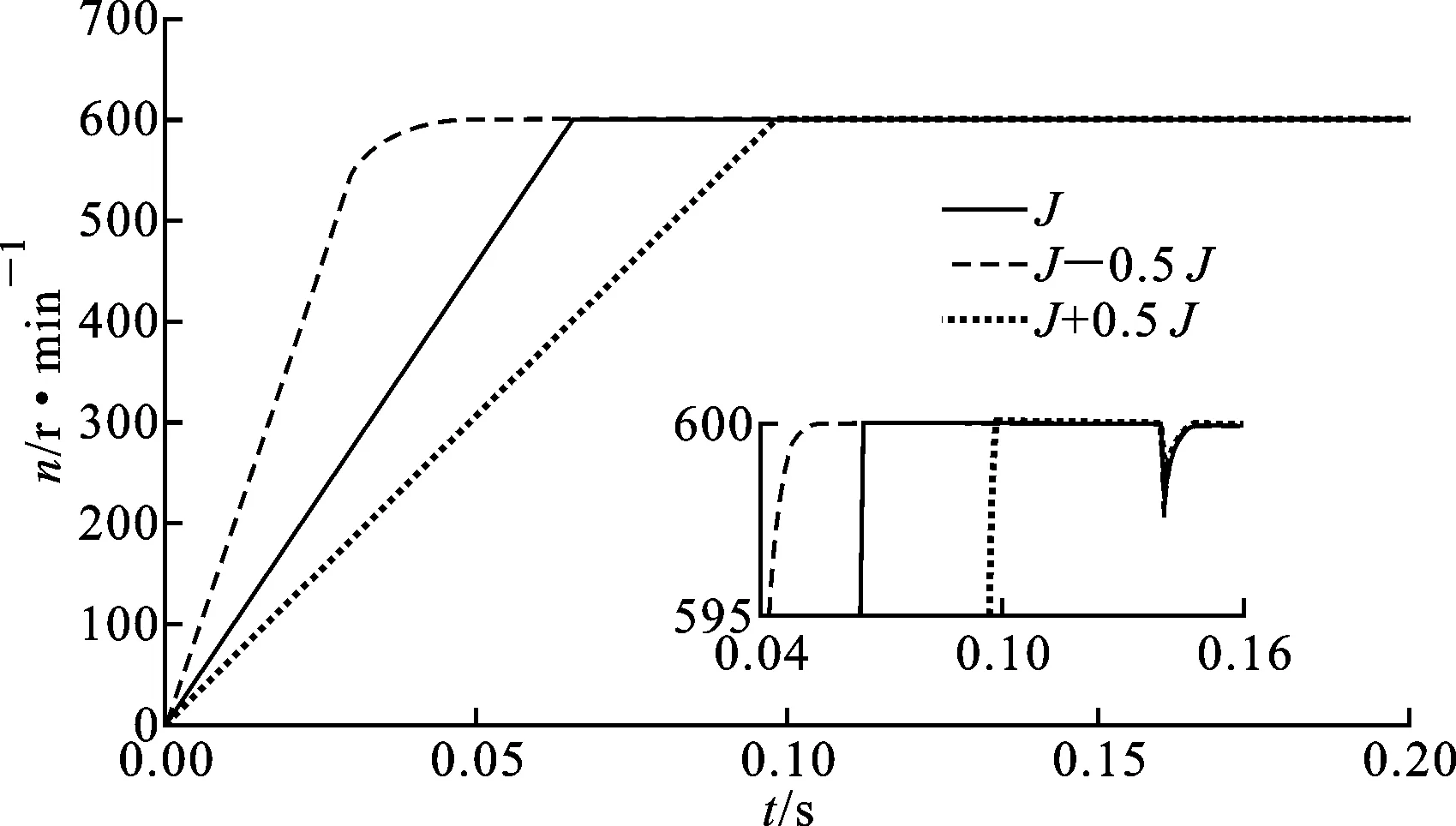
图10 不同转动惯量下NFTSM控制的转速响应

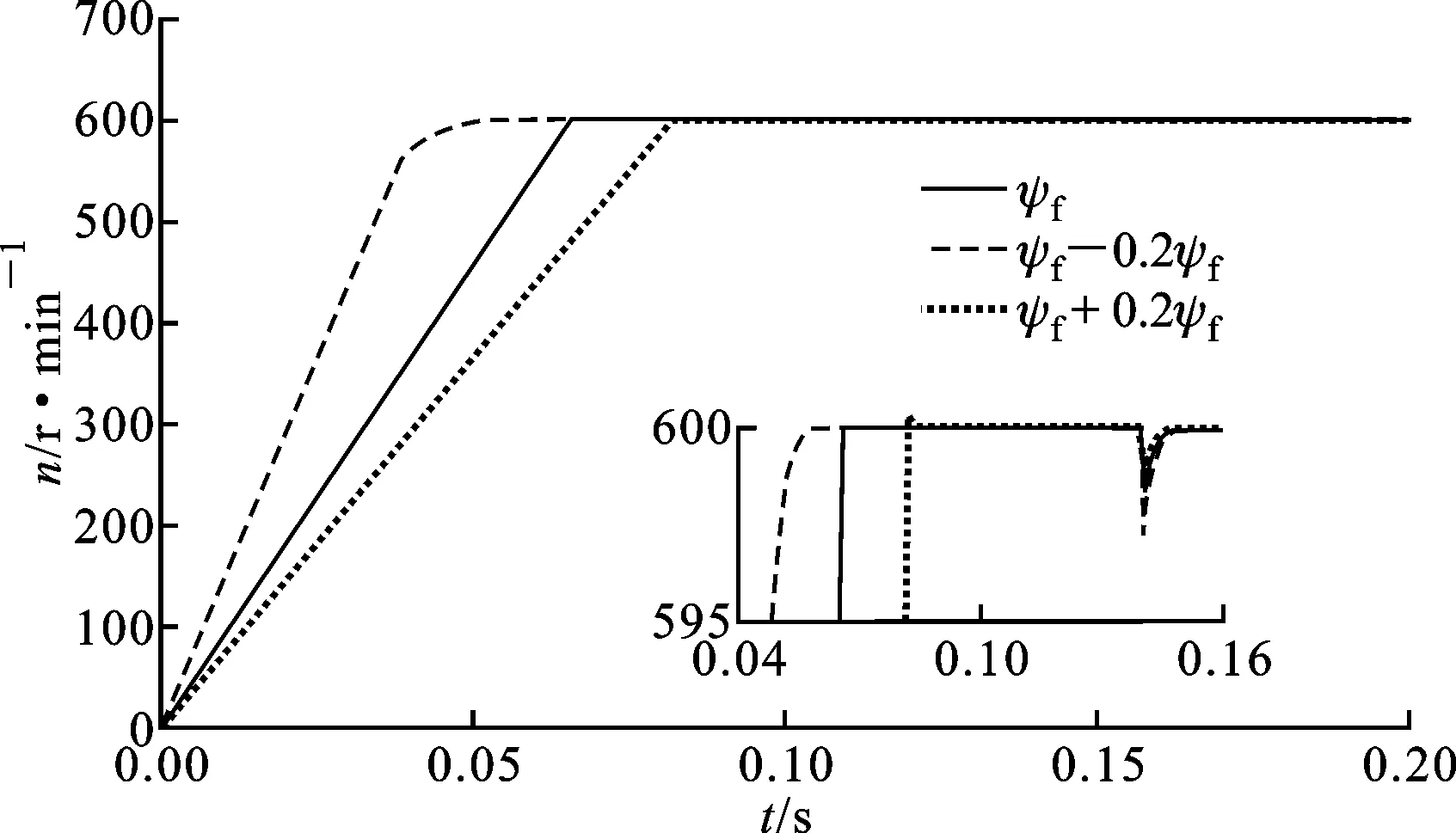
图11 不同磁通下NFTSM控制的转速响应

由图9～图11可见,当负载发生变化或存在参数摄动时,NFTSM控制仍能实现转速的动态快速响应、稳态精确跟踪,且几乎无振荡。

4 结 论

本文通过对矢量控制下的永磁同步电机调速系统,采用非奇异快速终端滑模速度控制器,根据二阶模型进行滑模速度控制器控制律的设计,采用可变边界层实现了抖振和跟踪精度的协调控制,并给出了稳定性分析。仿真结果表明,本文所提出的NFTSM控制器与PI控制器和NTSM控制器相比,电机转速误差能够更快地收敛至平衡点,超调量小,平衡点附近波动小,控制量抖振小,转速稳态精度高,并且对于负载扰动、参数扰动都具有较强的鲁棒性。因此,该方法在工程中具有广泛的应用前景。

[1]WANG M S, SYAMSIANA I N, LIN F C.Sensorless speed control of permanent magnet synchronous motors by neural network algorithm [J].Mathematical Problems in Engineering, 2014, 50(4): 1-7.

[2]LI Zhijun, YANG Chenguang, DING Nan, et al.Robust adaptive motion control for underwater remotely operated vehicles with velocity constraints [J].International Journal of Control, Automation and Systems, 2012, 10(2): 421-429.

[3]LI Zhijun, YANG Chenguang, TANG Yong.Decentralised adaptive fuzzy control of coordinated multiple mobile manipulators interacting with non-rigid environments [J].IET Control Theory & Applications, 2013, 7(3): 397-410.

[4]LEE T S, LIN C H, LIN F J.An adaptiveH∞controller design for permanent magnet synchronous motor drives [J].Control Engineering Practice, 2005, 13(4): 425-439.

[5]CHOI H H, JUNG J W.Fuzzy speed control with an acceleration observer for a permanent magnet synchronous motor [J].Nonlinear Dynamics, 2012, 67(3): 1717-1727.

[6]YANG Chenguang, ZHAI Lianfei, GE Shuzhi.Adaptive model reference control of a class of MIMO discrete-time systems with compensation of nonparametric uncertainty[C]∥ Proceedings of the American Control Conference.Piscataway, NJ, USA: IEEE, 2008: 4111-4116

[7]LIU Ling, LIANG Deliang, LIU Chongxin, et al.Nonlinear state observer design for projective synchronization of fractional-order permanent magnet synchronous motor [J].International Journal of Modern Physics: B, 2012, 26(30): 1250166.

[8]刘金琨, 孙富春.滑模变结构控制理论及其算法研究与进展 [J].控制理论与应用, 2007, 24(3): 407-418.

LIU Jinkun, SUN Fuchun.Research and development on theory and algorithms of sliding mode control [J].Control Theory & Applications, 2007, 24(3): 407-418.

[9]LIU Ling, DING Wen, LIU Chongxin, et al.Hyperchaotic synchronization of fractional-order arbitrary dimensional dynamical systems via modified sliding mode control [J].Nonlinear Dynamics, 2014, 76(4): 2059-2071.

[10]李政, 胡广大, 崔家瑞, 等.永磁同步电机调速系统的积分型滑模变结构控制 [J].中国电机工程学报, 2014, 34(3): 431-437.

LI Zheng, HU Guangda, CUI Jiarui, et al.Sliding-mode variable structure control with integral action for permanent magnet synchronous motor [J].Proceedings of the CSEE, 2014, 34(3): 431-437.

[11]倪骏康, 刘崇新, 庞霞.电力系统混沌振荡的等效快速终端模糊滑模控制 [J].物理学报, 2013, 62(19): 19057.

NI Junkang, LIU Chongxin, PANG Xia.Fuzzy fast terminal sliding mode controller using an equivalent control for chaotic oscillation in power system [J].Acta Physica Sinica, 2013, 62(19): 19057.

[12]袁雷, 沈建清, 肖飞, 等.插入式永磁低速同步电机非奇异终端滑模观测器设计 [J].物理学报, 2013, 62(3): 030501.

YUAN Lei, SHEN Jianqing, XIAO Fei, et al.Nonsingular terminal sliding-mode observer design for interior permanent magnet synchronous motor drive at very low-speed [J].Acta Physica Sinica, 2013, 62(3): 030501.

[13]HE Zhenxin, LIU Chuntong, ZHAN Ying, et al.Nonsingular fast terminal sliding mode control with extended state observer and tracking differentiator for uncertain nonlinear systems [J].Mathematical Problems in Engineering, 2014, 27(2): 1-16.

[14]赵鹏, 姚敏立, 沈晓卫, 等.非奇异快速终端滑模液位跟踪控制 [J].西安交通大学学报, 2011, 45(12): 39-44.

ZHAO Peng, YAO Minli, SHEN Xiaowei, et al.Tracking control of water level based on a nonsingular terminal sliding mode [J].Journal of Xi’an Jiaotong University, 2011, 45(12): 39-44.

[15]张希, 陈宗祥, 潘俊民, 等.永磁直线同步电机的固定边界层滑模控制 [J].中国电机工程学报, 2006, 26(22): 115-121.

ZHANG Xi, CHEN Zongxiang, PAN Junmin, et al.Fixed boundary layer sliding mode control of permanent magnet linear synchronous motor [J].Proceedings of the CSEE, 2006, 26(22): 115-121.

[16]林雷, 任华彬, 王洪瑞.基于径向基函数神经网络的机器人滑模控制 [J].控制工程, 2007, 14(2): 224-226.

LIN Lei, REN Huabin, WANG Hongrui.RBFNN-based sliding mode control for robot [J].Control Engineering of China, 2007, 14(2): 224-226.

[17]LIU Xiaodong, WU Yunjie, LIU Baiting.The research of adaptive sliding mode controller for motor servo system using fuzzy upper bound on disturbances [J].International Journal of Control, Automation, and Systems, 2012, 10(5): 1064-1069.

[18]YANG Jun, LI Shihua, YU Xinghuo.Sliding-mode control for systems with mismatched uncertainties via a disturbance observer [J].IEEE Transactions on Industrial Electronics, 2013, 60(1): 160-169.

[19]LI Shihua, ZONG Kai, LIU Huixian.A composite speed controller based on a second-order model of permanent magnet synchronous motor system [J].Transactions of the Institute of Measurement and Control, 2011, 33(5): 522-541.

(编辑 刘杨)

A Nonsingular Fast Terminal Sliding Mode Controller with Varying Boundary Layers for Permanent Magnet Synchronous Motors

CHANG Xuejian1, LIU Ling1, CUI Rongxin2

(1.School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2.College of Marine Engineering, Northwestern Polytechnical University, Xi’an 710072, China)

A nonsingular fast terminal sliding mode (NFTSM) controller with varying boundary layers is proposed to solve the problem that speed-regulation systems of permanent magnet synchronous motors (PMSM) are susceptible to parameter uncertainties and disturbances of external loads.The sliding mode control law for speed loop is developed through building the NFTSM surface with fast convergence in a finite time and using the second-order model of rotary speed andq-axis stator reference current so that the errors caused by the first-order model of rotary speed andq-axis stator reference current are decreased and the singular problem of the terminal sliding mode surface is avoided.Furthermore, the varying boundary layer is designed to make the system states switch to a small boundary layer when the error decreases to a threshold so that the coordinated control between chattering and tracking accuracy is realized.Numerical simulation results and a comparison with the traditional PI control show that the proposed NFTSM control scheme achieves smaller overshoot and faster response, and the steady-state error is near to zero.Moreover, the NFTSM has strong robustness in parameter variations and disturbances of external loads, and ensures a higher steady-state precision of the speed with a lower chattering.

permanent magnet synchronous motor; sliding mode control; second-order model; load disturbance; parameter variation

2014-12-19。 作者简介:常雪剑(1991—),女,硕士生;刘凌(通信作者),男,博士,讲师,硕士生导师。 基金项目:国家自然科学基金资助项目(51307130,61472325,51209174)。

时间:2015-03-19

http:∥www.cnki.net/kcms/detail/61.1069.T.20150319.1153.001.html

10.7652/xjtuxb201506009

TM301

A

0253-987X(2015)06-0053-07