基于附加动量的小波神经网络风电功率短期预测

刘晓楠，王胜辉 ，金月新

(沈阳工程学院a.电力学院 b.产业管理处,辽宁 沈阳 110136)



基于附加动量的小波神经网络风电功率短期预测

刘晓楠a，王胜辉b，金月新b

(沈阳工程学院a.电力学院 b.产业管理处,辽宁 沈阳 110136)

摘要：以风电功率预测为背景，将小波理论与神经网络结合，在BP神经网络模型的结构基础上构造了小波神经网络，并提出了基于附加动量法改进的小波神经网络。利用附加动量的小波神经网络建立天气预报数据与发电功率的映射模型，并进行实际预测。利用MATLAB进行仿真，验证了设计预测模型的实际可行性，并且预测精度满足相关要求。

关键词：风力发电；功率预测；BP神经网络；小波分析；小波神经网络

在电力方面，用于火力发电的天然气、煤炭、石油的化石燃料的消耗日益增多，不仅使得这些不可再生的资源面临枯竭的问题，也使得全球的环境问题日益增多，这些无疑都限制了火力发电的发展。为了解决能源危机以及环境问题，世界各国近几十年来在努力寻找能够替代化石能源的新能源，风能、太阳能、核能、生物质能等等纷纷登上历史舞台，对清洁的可再生的新能源的研究、开发及利用应运而生。其中风能凭借其清洁、可再生、分布广等众多优点而受到世界各国青睐，许多国家已经把发展风电作为解决能源和环境问题的重要措施。根据研究显示，每10 MW风电入网可节约3.73 t煤炭，同时减少排放粉尘0.498 t、CO 29.35 t、NOx0.049 t和SO20.078 t[1]。无论从短期还是从长期来看，风力发电都是电力可持续发展战略的最佳选择。

根据全球风能理事会(GWEC)2014年2月5日发布的2013年全球风电统计数据显示，截至2013年底，全球风电累计装机容量达到3.18亿kW，排名前五位依次为中国、美国、德国、西班牙、印度，在过去的五年(2009~2013年)全球风电市场规模扩大了几乎200 GW。新增装机容量排名前五位国家分别是中国、德国、英国、印度、加拿大。中国风电事业正经历着由分散小规模开发，向集中大规模远距离输送方向发展。中国已经成为世界风电大国，正在向风电强国转变。

传统的火力发电方式是根据负荷的需求来安排发电计划，但由于风具有随机性、波动性和间歇性等特点，使得风电场的发电功率具有很大的随机性且可控性相对较差。因此当大容量的风电接入电网时会严重影响电力系统的安全性、稳定行以及电能的质量。对风电场的发电功率进行比较准确可靠的预测，可以有效地降低风力发电对电网所带来的不利影响，并且能使电力调度部门合理安排调整调度计划，从而减少电力系统运行成本和旋转备用，使之获得更多的经济效益和社会效益。目前，在国家电网公司的发电计划制定中都应用了风电功率预测系统，这对解决大规模风电接入电网后的调度运行问题提供了强有力的技术支撑。

现在丹麦 、德国 、西班牙、英国以及美国等风电发展较为成熟的国家已经研发出多个用于风电场输出功率短期预测的系统，并成功应用于多个风电场[2]。与欧洲相比，由于我国风资源的分布特点致使大部分风电场建设较为集中，风能的间歇性对风电并网的影响更为突出。因此，开展适合我国风电情况的风电功率短期预测的研究与预测软件的开发对于我国实现大规模风电场的建设是非常必要的。

1小波神经网络方法

根据所参考查询的国内外文献资料，目前关于风电功率预测的方法研究比较成熟、使用较多的是神经网络法。神经网络具有学习能力，可以以任意精度逼近任意非线性映射。但神经网络容易出现对数据学习不够或者过拟合的现象，预测精度不太稳定等缺点。为此，有必要将更加优秀的预测方法引入到风电功率的预测当中来。由于小波变换对分析的信号具有时间和频率局部特性和自适应的聚焦特性，而神经网络具有自学习、自适应性、强鲁棒性和推广能力，如何把小波分析和神经网络两者的优势结合起来用于分析非平稳信号，一直是人们所关注的问题。

1.1　小波变换理论

1.1.1小波变换的发展

小波变换的概念是由法国工程师J.Morlet在20世纪70年代首先提出的，并于20世纪80年代开发出了连续小波变换。1986年著名数学家Y.Meyer构造了第一个正交小波—Meyer小波，这是一个真正的小波基。从1988年Stephane Mallat提出了Mallat快速算法(塔式分解和重构算法)之后，小波分析开始蓬勃发展起来，并在各个工程领域中得到了广泛的应用。目前，小波分析已成为信号处理的强有力工具，典型的如语音信号处理、医学信号处理、图像信息处理、机械故障诊断等。

1.1.2小波变换的原理

(1)

则称ψ(t)为一个基小波或母小波函数，它一般是时域上以t=0为中心的带通函数，在时域和频域都必须是局部化(紧支撑)的，且其平均值为零，即∫ψ(t)=0。小波可以简单的描述为一种函数，这种函数在有限时间范围内变化，并且平均值为0。

将母小波函数ψ(t)进行平移和伸缩得到ψa,b(t)，设其伸缩因子为a，平移因子为b，则

(2)

称ψa,b(t)为依赖于参数a，b的小波基函数。当a，b取值连续变化时，ψa,b(t)称为连续小波基函数。小波基函数的窗口随尺度因子的不同而伸缩，当a逐渐增大时，基函数ψa,b(t)的时间窗口也逐渐变大，而其对应的频域窗口也相应减小，中心频率逐渐变低。相反，当a逐渐减小时，基函数ψa,b(t)的时间窗口逐渐减小，而其频域窗口相应增大，中心频率逐渐升高。

小波变换通过平移基小波(mother wavelet)可获得信号的时间信息，而通过缩放小波的宽度(或者叫做尺度)可获得信号的频率特性。对基小波的缩放和平移操作是为了计算小波的系数，这些系数代表小波和局部信号之间的相互关系[3]。

1.2　小波神经网络的原理

最早研究小波变换与神经网络结合的是Pati和Krishnaprasad，并且首次提出了离散仿射小波网络的模型[4]。目前小波与神经网络的结合主要分为两种方式：一个是分离式结合，比较典型的是利用小波分析对信号进行预处理，然后将处理所得的各个信号分别用神经网络学习与训练；另一个是嵌套式结合，即把小波变换的运算融入到神经网络中去，将小波函数作为神经元的传递函数，形成所谓的小波神经网络(WNN)或小波网络。这是两者结合的主要方式，其中小波与前馈神经网络的嵌套式结合又是最主要的研究方向。小波神经网络是在小波分析研究基础上提出的一种前馈网络，它结合了小波分析与BP神经网络的优点，可以被认为是BP神经网络的推广，它在神经网络领域中具有良好的发展潜力。建立的小波神经网络以BP神经网络的结构为框架，将传递函数选用Morlet小波函数，其表达式为

h(x)=cos(1.75)e-x2/2

(3)

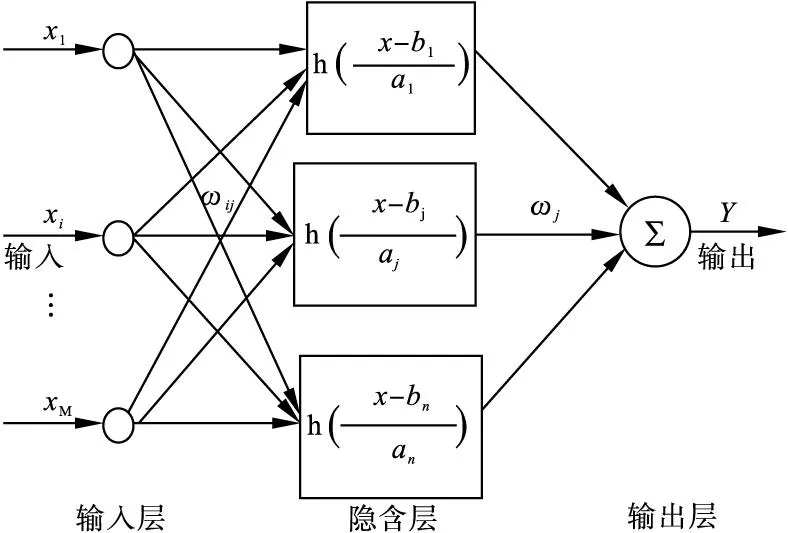
图1　WNN模型

其中：xi表示输入层第i个节点的输入，i=1,2,……,M；

ωij表示输入层第i个节点到隐含层第j个节点之间的权值；

aj表示隐含层第j个节点小波基函数的伸缩因子；

bj表示隐含层第j个节点小波基函数的平移因子；

h表示隐含层的小波函数；

ωj表示隐含层第j个节点和输出节点之间的权值，j=1,2,……,N;

Y表示输出节点的输出。

中间隐含层的处理函数为小波基函数，则隐含层的输出为

(4)

小波神经网络输出层输出计算公式为

(5)

其中，n为隐含层节点数。

小波神经网络权值参数和小波基函数参数的修正算法跟BP神经网络一样，从而使小波神经网络预测输出不断逼近期望输出。

网络对K个训练样本的总误差函数为

(6)

根据预测误差E的梯度下降法修正小波神经网络权值和小波基函数的参数，第p+1次修正值为

(7)

其中Δωij，Δaj，Δbj，Δωj是根据网络预测误差计算得到

(8)

BP网络算法的各种改进学习算法同样适用于小波神经网络训练和学习。针对传统的BP神经网络而言，其学习速率的不变性导致网络收敛速度很慢，容易陷入局部极小且训练时间加长。提出采用基于附加动量法的小波神经网络来进行风电功率预测。

带有附加动量因子的权值和阈值调节公式为

(9)

(10)

其中，p为训练次数，δj为局部梯度，Oi为上一层的输出，η为学习速率，mc为动量因子，一般取0.95左右。

改进后的小波神经网络的第p+1次的权值和小波函数参数修正值为

(11)

3基于附加动量法的小波神经网络实例分析

根据国家能源局发布的《风电场功率预测预报管理暂行办法》规定[5]：风电功率预测报告风日预报和实时预报两种方式。日预报是指对次日0时至24时的预测报告，实时预报是指自上报时刻起未来15min。日预报要求并网电场每日在规定时间前按规定要求向调度部门提交次日0是至24时每15min共96个点风电有功功率预测数据和开机容量。实时预测要求并网风电场按规定要求每15min滚动上报未来15min至4h风电功率预测数据。风电场功率预测系统提供的日预测曲线最大误差不超过25%；实时预测误差不超过15%；全天预测结果的均方根误差应小于20%。

风电场发电功率的评价指标可以分为误差评价指标和预测考核指标。误差评价指标主要包括平均绝对误差(MAE)和均方根误差(RMSE)，主要用来衡量预测效果的好坏；预报考核指标主要包括合格率和准确率，主要用于判断预测系统是否满足并网对预测结果的要求。

MAE、RMSE、准确率和合格率的计算公式如下：

(12)

(13)

(14)

(15)

其中，Bt的取值条件为

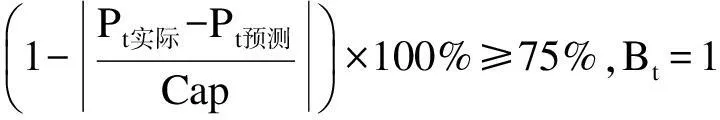
其中，Pt实际为t时刻的实际功率；Pt预测为t时刻的预测功率；Cap为装机容量；T为样本个数。

所选取的数据均来源自位于内蒙古通辽市开鲁县义和塔拉的深能北方(通辽)能源开发有限公司的深能义和风电场。该风电场一总装机容量为150MW，共安装了100台由东方汽轮机有限公司生产的单机容量为1.5MW的FD77B型风力发电机。该风电场提供的数据包括两类，一类是提前24h的时间间隔为15min的数值天气预报数值，包括风速、风向、温度、湿度、压力；一类是风电场通过SCADA系统采集的时间间隔为15min的实测风速、风向等天气数据以及风电场的发电功率。实例中应用的数据样本为深能义和风电场4月份2号至30号29天的数值天气预报数据与风电场实际输出功率，其中12号、15号、29号的数据缺失。数值天气预报数据与风电场实际输入功率均为每15min采样数据，因此共2 496 个样本。其中前2 400个数据为训练样本，后96个样本为测试样本。

利用MATLAB进行预模型的建立，分别采用BP神经网络和附加动量的小波神经网络方法来建立风电场发电功率预测模型。输入样本在输入样本之前利用MATLAB的mapminmax函数默认将数据归一化到[-1,1]。利用该函数将风速、温度，压力以及实测功率进行归一化处理，风向的归一化采用其正弦值和余弦值。在得到归一化后的预测值之后，把预测值还原为原来的量纲后与目标值进行比较来分析两种模型的误差大小。

把预测模型设计为由输入层、隐含层和输出层三层构成的BP神经网络。如果输入变量将数值天气预报的所有预报项都考虑进去，则输入层神经元数量为6个。按照神经网络构建经验选择隐含层神经元个数为输入层神经元个数的2倍加1，所以取隐含层神经元个数为13个。输出层的输出主要是风电场的发电功率，所以输出层神经元个数为1个，建立的模型如图2。

分别利用BP神经网络和附加动量的小波神经网络来对该风电场的发电功率进行预测，得到的各评价指标结果如表1所示。

BP神经网络得到的预测功率与实际功率的对比图如图3和图4和所示。通过采用附加动量法的小波神经网络得到的预测功率与实际功率的对比图如图5和图6所示。

图2　模型结构

表1　各种模型的评价指标

图3　BP神经网络结果对比图

从上面4个图中可以直观看出不同时间段风电功率预测功率值与实际功率的偏差。通过观察可以发现当实际的风电功率比较平稳或者波动不太大时，预测功率与实际功率的变化情基本相似。但当实际风电功率突变时，此时预测功率往往出现比较大的偏差，预测功率不太稳定可靠。

图4　BP神经网络结果误差图

图5　采用附加动量法的小波神经网络结果对比图

图6　采用附加动量法的小波神经网络对比图和误差图

所建立的附加动量法小波神经网络预测模型的预测结果基本符合国家颁布的风电场功率预报管理暂行办法的通知中的相关要求，因此利用该模型来预测未来一天的风电场发电输出功率具有实际可行性。

4结语

利用某风电场提供的数值天气预报数据和实测功率数据，将理论模型用于实际的预测中去。分别利用传统的BP神经网络和改进过后的基于附加动量的小波神经网络进行建模预测，结果表明所提出的基于附加动量的小波神经网络具有更好的预测精度。但是，有个别预测点的误差还是不尽如人意，预测精度有待于进一步提高。目前，风力发电功率预测仍然存在着许多的困难，预测精度还是能够进一步得到提高的。应该在不断学习国外先进方法的同时，立足本国的实际情况进行改善，从而更好地促进新能源的开发以及新兴电力事业的发展。

参考文献

[1]潘广德,张铁,林子超.浅谈风力发电及其发展[J].科技向导,2013(14):72.

[2]GiebelG,LandbergL,KariniotakisG,etal.State-of-the-artonMethodsandSoftwareToolsofShort-TermPredictionofWindEnergyProduction[C]//EuropeanWindEnergyConference&ExhibitionEWEC2003,Marid,2003.

[3]孔莹莹.微小卫星JPEG2000图像压缩与遥测信息复合编码的设计与实现[D].南京：南京航空航天大学，2006.

[4]PatiYC,KrishnaprasadPS.Analysisandsynthesisoffeedforwardneuralnetworkusingdiscreteaffinewavelet.IEEEtransonNN,1993,4(1):73-75.

(责任编辑佟金锴校对张凯)

WindPowerShortTermForecastingBasedontheAdditional

MomentumofWaveletNeuralNetwork

LIUXiao-nana,WANG Sheng-huia,JIN Yue-xinb

(a.SchoolofElectricalEngineering,b.IndustryManagementOffice,ShenyangInstituteof

Engineering,Shenyang110136,LiaoningProvince)

Abstract：Against the background of the wind power forecasting,the wavelet theory and neural network were combined to set up the WNN model based on the BPNN structure,and the WNN was put forward based on the additional momentum method in this paper.A model was set up with the method based on the numerical weather prediction data and wind power data from a wind farm in Inner Mongolia Autonomous Region.The MATLAB was used to simulate and verify the feasibility of this prediction model.Simulation had shown the precision of the model can meet the requirements.

Key words：Wind power;Wind power forecasting;BPNN;Wavelet analysis;WNN

通讯作者：王胜辉(1964-)，男，辽宁本溪人，教授，博士，硕士生导师，主要从事电机与电器方面的研究。

作者简介：刘晓楠(1989-)，女，四川绵阳人，硕士研究生。

基金项目：国家自然基金资助项目(61372195)

收稿日期：2014-11-12

中图分类号：TM715

文献标识码：A

文章编号：1673-1603(2015)02-0101-06

DOI：10.13888/j.cnki.jsie(ns).2015.02.002