参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用

唐贵基,王晓龙

(华北电力大学能源动力与机械工程学院,071000,河北保定)



参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用

唐贵基,王晓龙

(华北电力大学能源动力与机械工程学院,071000,河北保定)

针对滚动轴承早期故障特征提取困难的问题,提出一种基于参数优化变分模态分解的轴承早期故障诊断方法。首先利用粒子群优化算法对变分模态分解算法的最佳影响参数组合进行搜索,搜索结束后根据所得结果设定变分模态分解算法的惩罚参数和分量个数,并利用参数优化变分模态分解算法对故障信号进行处理。原故障信号经过处理后被分解为若干本征模态函数分量,由此筛选出最佳信号分量并进行包络解调运算,最终通过分析信号的包络谱可判断轴承的故障类型。利用参数优化变分模态分解方法对轴承故障仿真和实测信号进行分析,均成功提取出微弱特征频率信息,表明参数优化变分模态分解方法可实现滚动轴承早期故障的有效判别,具有一定的可靠性和应用价值。

变分模态分解;粒子群算法;滚动轴承;早期故障诊断

滚动轴承是机械设备中的重要零部件,故障率高、易损坏,如果能在故障早期阶段有效提取出故障特征信息,实现轴承运行状态的准确判别,并对损伤的轴承进行及时的更换或修复,则可有效避免连锁故障的发生,对于减少经济损失意义重大[1-2]。

经验模态分解(EMD)[3]作为一种自适应信号处理方法,一经提出就受到机械故障诊断领域相关学者的广泛关注,并在滚动轴承故障特征提取上得到了成功应用[4-6]。EMD方法本质上是一个二进制滤波器组[7],这种信号频域分割特性使得EMD方法在处理轴承故障信号时难免存在弊端。由于与故障相关的信号频带的中心及带宽均不确定,所以如果故障相关频带处于第一个分解分量的频带内,可能会因为该分量的频带过宽而引入过多干扰,如果故障相关频带位于更高阶次分解分量的频带内,则可能因为分量的频带过窄而遗漏重要的特征信息。

2014年Dragomiretskiy等人提出一种自适应信号处理新方法——变分模态分解(VMD)[8],该方法在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽,从而能够自适应地实现信号的频域剖分及各分量的有效分离。由于VMD方法刚刚提出,尚未得到推广,因此其在实际工程中的应用还未见报道。笔者尝试将其引入到机械故障诊断领域,用于分析滚动轴承早期微弱故障信号。VMD算法的信号处理结果同时受惩罚参数以及分量个数这两个参数的影响,为了从信噪比较低的轴承早期故障信号中分离出包含丰富特征信息的信号分量,实现最佳的处理效果,本文利用粒子群算法对VMD算法的最佳影响参数组合进行了搜寻,提出了基于参数优化变分模态分解的轴承早期故障诊断方法。仿真信号和实测信号分析结果表明,该方法可有效提取轴承早期故障特征信息,实现故障类型的准确判别。

1 变分模态分解

VMD算法中,本征模态函数(IMF)被重新定义为一个调幅-调频信号,表达式为[8]

uk(t)=Ak(t)cos(φk(t))

(1)

VMD算法在获取IMF分量时摆脱了EMD算法所使用的循环筛分剥离的信号处理方式,而是将信号分解过程转移到变分框架内,通过搜寻约束变分模型最优解来实现信号自适应分解,每个IMF分量的频率中心及带宽在迭代求解变分模型的过程中不断更新,最终可根据实际信号的频域特性完成信号频带的自适应剖分,得到若干窄带IMF分量。假定将原始信号分解为K个IMF分量,则对应的约束变分模型表达式如下

(2)

式中:{uk}={u1,…,uK}代表分解得到的K个IMF分量;{ωk}={ω1,…,ωK}表示各分量的频率中心。

为求取上述约束变分问题的最优解,引入如下形式的增广Lagrange函数,即

(3)

式中:α为惩罚参数;λ为Lagrange乘子。

利用交替方向乘子算法求取上述增广Lagrange函数的鞍点,即为式(3)约束变分模型的最优解,从而将原始信号分解为K个窄带IMF分量。具体实现过程如下:

(2)n=n+1,执行整个循环;

(3)执行内层第一个循环,根据

更新uk;

(4)k=k+1重复步骤(3),直至k=K,结束内层第一个循环;

(5)执行内层第二个循环,根据

更新ωk;

(6)k=k+1重复步骤(5),直至k=K,结束内层第二个循环;

2 基于粒子群优化的变分模态分解

由于VMD算法与EMD算法分别建立在截然不同的理论框架上,因此二者之间存在诸多差异,其中一个较大差别就是利用VMD算法处理信号时需要预先设定分解所得IMF分量的个数,分量个数K设置得不同,最终处理结果也将不同。经过深入研究发现,VMD算法中惩罚参数α对分解结果也存在较大影响,α越小,所得各个IMF分量的带宽越大,反之,分量信号的带宽越小。由于实际待分析信号复杂多变,因此K和α这两个影响参数通常难以确定,如何选定合适的参数组合,是利用VMD算法分析轴承早期故障信号的关键所在。

如果保持一个影响参数不变,仅以另一个影响参数为优化对象,讨论该参数对处理结果的影响,这种局部寻优方式忽略了两个影响参数间的交互作用,得到的只是相对最优结果。粒子群算法[9]作为一种群体智能优化算法,具有良好的全局寻优能力,因此本文利用粒子群算法对VMD算法的两个影响参数进行并行优化,从而可避免人为主观因素的干预,自动筛选出最佳的影响参数组合。

假设在一个D维空间中,由M个粒子组成的种群为X=(X1,X2,…,XM),第i个粒子在D维搜索空间中的位置为Xi=(xi1,xi2,…,xiD)(即优化问题的潜在解),第i个粒子的速度为Vi=(vi1,vi2,…,viD),其个体局部极值为Pi=(pi1,pi2,…,piD),种群全局极值G=(g1,g2,…,gD),每个粒子通过个体局部极值和种群全局极值迭代更新自身的速度和位置,表述为[10-11]

(4)

式中:w为惯性权重;d=1,2,…,D;i=1,2,…,M;k为当前迭代次数;c1和c2为加速度因子;η为介于[0,1]间的随机数。

利用粒子群算法搜寻VMD算法的影响参数时,需确定一个适应度函数,粒子每次更新位置时计算一次适应度值,通过对比新粒子适应度值进行更新。Shannon熵是一种很好的评价信号稀疏特性的标准,熵值的大小反映了概率分布的均匀性,最不确定的概率分布(等概率分布)具有最大的熵值[12]。本文在此基础上提出包络熵的概念,将信号解调运算后得到的包络信号处理成一个概率分布序列pj,由它计算得到的熵值就反映了原始信号的稀疏特性。零均值信号x(j)(j=1,2,…,N)的包络熵Ep可表示成

(5)

式中:pj是a(j)的归一化形式;a(j)是信号x(j)经Hilbert解调后得到的包络信号。

(1)初始化粒子群算法的各项参数并确定寻优过程中的适应度函数。

(2)初始化粒子种群,以影响参数组合[α,K]作为粒子的位置,随机产生一定数量的影响参数组合作为粒子的初始位置,随机初始化每个粒子的移动速度。

(4)对比适应度值大小并更新个体局部极值和种群全局极值。

(5)利用式(4)更新粒子的速度和位置。

(6)循环迭代,转至步骤(3),直至迭代次数达到最大设定值后输出最佳适应度值及粒子的位置。

3 诊断流程

轴承早期故障引起的周期性冲击能量微弱,并且受环境噪声及信号衰减的影响,故障特征提取相对困难。本文尝试利用VMD方法来分析轴承早期故障信号,并利用粒子群算法搜寻VMD算法的最佳影响参数组合,由此提出了基于参数优化变分模态分解的滚动轴承早期故障诊断方法,图1为诊断流程,具体实现步骤如下。

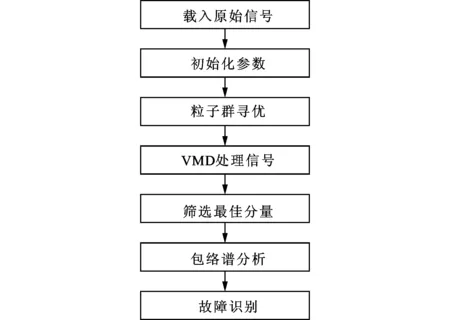
图1 轴承早期故障诊断流程图

(1)设定粒子群算法各参数并搜寻VMD算法的α及K,参考文献[10]进行参数的设定。本文粒子群算法设定的各项参数如表1所示,表中Gmax为最大进化代数;M为种群规模。

表1 粒子群算法各项参数

(2)粒子群寻优结束后会得到一组最佳影响参数组合[αo,Ko],设定VMD算法的惩罚参数为αo,分量个数为Ko,并利用影响参数优化后的VMD算法对轴承早期故障信号进行处理。

(3)故障信号经VMD算法处理后得到若干IMF分量,将包络熵值最小的分量,即与局部极小熵值相对应的IMF分量作为最佳分量,计算该分量的包络谱。

(4)将轴承故障特征频率理论值与包络谱中幅值明显的谱线进行对比,实现故障判别。

4 仿真信号分析

为验证本文方法的有效性,利用故障模型[13]模拟了轴承内圈故障产生的冲击信号,并向其中添加强烈白噪声以模拟内圈早期故障信号,仿真信号如下

(6)

式中:s(t)为周期性冲击信号;A0=0.3为幅值初值;fr=20 Hz为转频;C=700为衰减系数;fn=3 000 Hz为共振频率;fi=1/T=80 Hz为内圈故障特征频率;n(t)为高斯白噪声。染噪信号的信噪比RSNR=20lg(υs/υn)=-13 dB,其中υs和υn分别为冲击和噪声的有效值,fs=12 kHz为采样频率,分析点数为8 192。图2为冲击信号的仿真信号波形及频谱。对比图2a、b发现,强烈的背景噪声将仿真信号中的周期脉冲完全淹没,毫无规律可循,频谱中共振频带也不明显。图3为仿真信号的包络谱,从中也未发现任何突出频率成分。

(a)冲击信号波形

(b)仿真信号波形

(c)仿真信号频谱图2 冲击信号的仿真信号波形及频谱

图3 仿真信号包络谱

图4是利用本文方法对仿真信号进行分析后的结果。粒子群寻优过程中局部极小熵值随种群进化代数的变化见图4a,显然局部极小熵值的最小值8.846出现在第7代,搜寻到的最佳影响参数组合[αo,Ko]=[261,7],由此设定VMD算法的α=7、K=7,并对仿真信号进行处理。原始信号经参数优化变分模态分解算法处理后得到的7个IMF分量(IMF1～IMF7)的波形及频谱见图4b。通过仔细观察可以发现,相比于其他分量,IMF4波形中规律性冲击更加明显,其频带中心恰好处于3 000 Hz,在共振频率附近,所有分量中IMF4的包络熵值也是最小的,该分量即是与局部极小熵值相对应的最佳分量。对其做进一步包络解调运算,得到图4c所示的包络谱,其中特征频率及倍频fi～3fi处谱线幅值十分突出,说明特征频率信息被提取了出来。

(a)局部极小熵值随进化代数的变化

(b)VMD处理后的信号波形和频谱

(c)IMF4分量的包络谱图4 本文方法对仿真信号的分析结果

为验证本文方法的优势,利用EMD算法对上述仿真信号进行了处理,并做包络解调运算,取其最佳包络谱(所有分量均做包络谱,取效果最好的一个)与本文方法进行了对比。图5为仿真信号EMD处理后的结果,共获得了11个分解分量(C1～C11)。经过对比发现,仅C1分量的包络谱中出现了特征频率相关成分,解调效果最佳,结果见图5b,但与图4c相比,故障特征频率及其二倍频处谱线幅值并不突出,背景噪声严重,干扰谱线过多,分析效果不佳。

(a)EMD处理后的信号波形和频谱

(b)C1分量的包络谱图5 仿真信号的EMD分析结果

5 实测信号分析

5.1 人为植入故障试验信号

为验证本文方法对实测振动信号分析的有效性,利用实际滚动轴承故障信号进行了验证。图6为测试试验平台。在试验台右侧的轴承上人为植入故障,利用电火花加工的方式,在轴承的单个圆柱滚动体上制造了一个直径约为0.8 mm、深度约为1 mm的微小凹坑,从而模拟轴承滚动体早期故障缺陷。加速度传感器位于轴承座上方,拾取振动信号时转轴转速为1 480 r/min,采样频率为12.8 kHz。表2为试验轴承的结构参数。根据结构参数计算得到的滚动体理论故障特征频率fe=123.5 Hz。

图6 测试试验平台

轴承型号轴承节径/mm滚动体直径/mm滚动体个数接触角/(°)N2053975120

图7为滚动体故障信号的波形及谱图。时域波形中仅个别位置存在较大冲击,规律性不明显,频谱中1 000～2 000 Hz间存在一个共振频带,低频段未发现故障相关频率成分。对故障信号直接做包络解调运算,得到图8所示的包络谱,其中故障特征频率fe存在一个微小谱峰,但并不明显,很难就此对轴承状态做出准确判断。

(a)故障信号波形

(b)故障信号频谱图7 故障信号的波形及频谱

图8 故障信号的包络谱

下面利用本文方法对滚动体故障信号进行分析,结果如图9所示。图9a为局部极小熵值随进化代数的变化,粒子群仅进化到了第4代就得到局部极小熵值的最小值8.574 7,寻优得到的[α,K]的最佳组合为[209,6]。在完成VMD算法参数设定后对原始信号进行处理,所得6个分量中IMF5分量的包络熵值最小(篇幅所限,处理结果省略),是与局部极小熵值相对应的最佳分量,该分量的波形见图9b。通过观察发现,与原始信号相比,IMF5分量中原本较大的冲击脉冲变得更加明显,并出现了许多原始信号中观察不到的幅值较小的冲击,由此表明经参数优化变分模态分解算法处理后,淹没于背景噪声中的与故障相关的成分被剥离了出来。对IMF5分量做进一步包络谱分析的结果见图9c,其中滚动体故障特征频率fe及其二倍频2fe处出现了清晰的峰值谱线,由此可断定轴承滚动体存在局部损伤,该分析结果与实际情况一致。

(a)局部极小熵值随进化代数的变化

(b)IMF5分量的时域波形

(c)IMF5分量的包络谱图9 本文方法的故障信号分析结果

同样,利用EMD算法对滚动体故障信号进行了处理(篇幅所限,处理结果省略),并取其最佳包络谱与本文方法进行了对比。EMD处理后共获得10个分解分量,其中C1的解调效果最佳,图10为该分量的波形及包络谱。对比后发现,图10b所示包络谱中干扰谱线偏多,不如图9的效果。

(a)C1分量的波形

(b)C1分量的包络谱图10 故障信号的EMD分析结果

5.2 全寿命周期加速试验信号

为进一步验证本文方法对实测振动信号分析的有效性,对NSFI/UCR智能维护系统中心的滚动轴承全寿命周期加速试验数据进行了分析[14]。试验台转轴上同时安装了4个轴承,转速为2 000 r/min,在每个轴承的轴向和径向上各安装了一个加速度传感器,图11为轴承和传感器的安装位置。

图11 轴承和传感器的安装位置

设置采样频率为20 kHz,在试验平台上共进行了3组全寿命加速试验,其中第2组试验持续了164 h,共采集984个文件,采样间隔为10 min,每次采集20 480个点。试验结束后发现,1号轴承外圈出现局部损伤,说明第2组试验中只有该轴承的数据为全寿命数据,本文便对该轴承的实测数据进行了分析。表3为试验滚动轴承结构参数。根据结构参数计算得到的外圈理论故障特征频率fe=236.4 Hz。图12为1号轴承振动信号的均方根值变化。

表3 滚动轴承结构参数

图12 1号轴承振动信号的均方根值变化

均方根值变化趋势基本反映了轴承从正常状态到故障状态的全过程。在7 020 min之前,轴承运行相对稳定;运行至7 020 min时,均方根值发生微小突变,表明轴承状态发生异常;在7 020～9 000 min时间段,均方根值上下浮动,但变化幅度不大,说明故障程度并不严重;运行至9 000 min后,均方根值呈递增趋势,并在9 790 min时达到最大,此时轴承已达到寿命极限。选择4 200 min时测得的信号进行分析,分析点数为8 192。图13为实测信号波形及频谱,可见时域波形中没有过于突出的冲击脉冲,频谱低频段未找到故障特征频率。图14为实测信号的直接包络谱分析结果,显然也没有出现与故障特征频率相关的成分。由此表明,传统直接包络解调方法对于该组信号来说无能为力。

(a)实测信号的波形

(b)实测信号的频谱图13 实测信号的波形及频谱

图14 实测信号的包络谱

图15是利用本文方法对实测信号进行分析后的结果。图15a中,粒子种群进化到第8代时得到局部极小熵值的最小值8.822 6及[α,K]的最佳组合[94,6],VMD处理所得结果中IMF2分量是与局部极小熵值相对应的最佳分量,该分量的波形见图15b。与原实测信号相比,很容易发现IMF2分量中规律性脉冲明显增多,信号中被噪声所淹没的周期性冲击成分被突显出来。图15c为该分量的包络谱,其中外圈故障特征频率fe存在一个明显谱峰,表明轴承外圈已经出现局部损伤,理论分析与实际情况相符。与均方根值指标相比,本文方法可提前2 820 min识别出轴承故障,这对于实际诊断应用来说意义重大。

(a)局部极小熵值随进化代数的变化

(b)IMF2分量的波形

(c)IMF2分量的包络谱图15 本文方法的实测信号分析结果

利用EMD算法对实测信号进行处理后共获得11个分量,分别进行包络解调后发现,仅C2的包络谱中出现了与特征频率相关的成分,图16为该分量的波形及包络谱,但图16b中外圈故障特征频率处谱线幅值并不突出,很容易造成漏诊。

(a)C2分量的波形

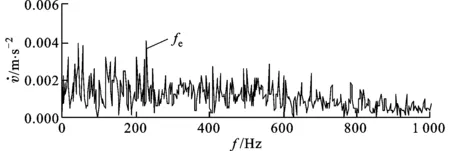
(b)C2分量的包络谱图16 实测信号的EMD分析结果

6 结 论

(1)滚动轴承早期故障特征信号微弱,特征提取相对困难,利用参数优化变分模态分解方法来分析轴承早期故障信号,可有效提取出微弱特征频率信息,实现轴承状态的准确判别。

(2)仿真及实测信号分析结果表明,在轴承微弱故障特征提取上,与传统直接包络解调方法和基于EMD的包络解调方法相比,参数优化变分模态分解方法的分析效果更为准确、有效,优势明显。

(3)VMD作为一种自适应信号处理新方法,尚未在实际工程领域得到应用。本文将其移植应用于机械故障诊断领域,利用该方法来分析轴承早期故障信号,旨在起到一个抛砖引玉的作用,尝试将其应用于其他类型机械故障诊断值得进一步深入研究。

[1] 梅检民, 肖云魁, 贾继德, 等. 基于改进阶比的变速器微弱故障特征提取 [J]. 振动工程学报, 2012, 25(3): 317-322. MEI Jianmin, XIAO Yunkui, JIA Jide, et al. Weak fault characteristics extraction for automobile transmission based on improved order analysis [J]. Journal of Vibration Engineering, 2012, 25(3): 317-322.

[2] 冯辅周, 司爱威, 饶国强, 等. 基于小波相关排列熵的轴承早期故障诊断技术 [J]. 机械工程学报, 2012, 48(13): 73-79. FENG Fuzhou, SI Aiwei, RAO Guoqiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy [J]. Journal of Mechanical Engineering, 2012, 48(13): 73-79.

[3] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society: A, 1998(454): 903-993.

[4] DU Qiuhua, YANG Shunian. Application of the EMD method in the vibration analysis of ball bearings [J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2634-2644.

[5] 程军圣, 于德介, 杨宇. 基于EMD的能量算子解调方法及其在机械故障诊断中的应用 [J]. 机械工程学报, 2004, 40(8): 115-118. CHENG Junsheng, YU Dejie, YANG Yu. Energy operator demodulating approach based on EMD and its application in mechanical fault diagnosis [J]. Journal of Mechanical Engineering, 2004, 40(8): 115-118.

[6] 李辉, 郑海起, 唐立伟. 声测法和经验模态分解在轴承故障诊断中的应用 [J]. 中国电机工程学报, 2006, 26(15): 124-128. LI Hui, ZHENG Haiqi, TANG Liwei. Application acoustic emission and empirical mode decomposition to faults diagnosis of bearing [J]. Proceedings of the CSEE, 2006, 26(15): 124-128.

[7] FLANDRIN P, RILLING G, GONCALVES P. Empirical mode decomposition as a filter band [J]. IEEE Signal Processing Letters, 2004, 11(2): 112-114.

[8] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition [J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

[9] KENNEDY J, EBERHART R C. Particle swarm optimization [C]∥IEEE International Conference on Neural Networks. Piscataway, NJ, USA: IEEE, 1995: 1942-1948.

[10]沈伋, 韩丽川, 沈益斌. 基于粒子群算法的飞机总体参数优化 [J]. 航空学报, 2008, 29(6): 1538-1541. SHEN Ji, HAN Lichuan, SHEN Yibin. Optimization of airplane primary parameters based on particle swarm algorithm [J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1538-1541.

[11]李宁. 粒子群优化算法的理论分析与应用研究 [D]. 武汉: 华中科技大学, 2006.

[12]蒋永华, 汤宝平, 刘文艺, 等. 基于参数优化Morlet小波变换的故障特征提取方法 [J]. 仪器仪表学报, 2010, 31(1): 56-60. JIANG Yonghua, TANG Baoping, LIU Wenyi, et al. Feature extraction method based on parameter optimized Morlet wavelet transform [J]. Chinese Journal of Scientific Instrument, 2010, 31(1): 56-60.

[13]王宏超, 陈进, 董广明. 基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取 [J]. 机械工程学报, 2013, 49(1): 88-94. WANG Hongchao, CHEN Jin, DONG Guangming. Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition [J]. Journal of Mechanical Engineering, 2013, 49(1): 88-94.

[14]LIN J, ZUO M J, FYFE K R. Mechanical fault detection based on the wavelet de-noising technique [J]. Journal of Vibration and Acoustics, 2004, 126: 9-16.

[本刊相关文献链接]

田福庆,罗荣,李万,等.改进的卷积型小波包分解及在故障诊断中的应用.2014,48(3):89-95.[doi:10.7652/xjtuxb 201403017]

杨清宇,孙凤伟.一种迭代改进的球向量机故障诊断算法.2013,47(10):1-6.[doi:10.7652/xjtuxb201310001]

夏虎,庄健,于德弘.面向高维特征故障数据的进化软子空间聚类算法.2013,47(5):115-120.[doi:10.7652/xjtuxb2013 05021]

胡小秋,陈维福.角接触球轴承热特性分析及试验.2015,49(2):106-110.[doi:10.7652/xjtuxb201502018]

周子超,王伊卿,吴文武,等.机床主轴轴承热诱导预紧力及刚度计算与实验研究.2015,49(2):111-116.[doi:10.7652/xjtuxb201502019]

金海善,朱爱斌,陈渭.利用改进牛顿-拉夫逊法的高速圆柱滚子轴承打滑分析.2015,49(1):133-138.[doi:10.7652/xjtuxb201501022]

位文明,吕盾,张俊,等.转台轴承静刚度建模及其影响因素分析.2014,48(12):8-14.[doi:10.7652/xjtuxb201412002]

翟强,闫柯,张优云,等.高速角接触球轴承腔内气相流动与传热特性研究.2014,48(12):29-33.[doi:10.7652/xjtuxb 201412005]

陈汝刚,陈韬.温度影响下箔片动压止推轴承分析.2014,48(11):32-36.[doi:10.7652/xjtuxb201411006]

李建栋,朱永生,熊青青,等.定压预紧主轴轴向动态刚度特性研究.2014,48(10):126-130.[doi:10.7652/xjtuxb2014 10020]

易均,刘恒,刘意,等.歪斜安装对组配轴承转子系统动力学特性影响.2014,48(9):107-111.[doi:10.7652/xjtuxb201409 018]

耿涛,孟庆丰,贾谦,等.薄衬层结构滑动轴承润滑膜厚度的超声检测方法.2014,48(8):80-85.[doi:10.7652/xjtuxb 201408014]

(编辑 苗凌)

Parameter Optimized Variational Mode Decomposition Method with Application to Incipient Fault Diagnosis of Rolling Bearing

TANG Guiji, WANG Xiaolong

(School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding, Hebei 071000, China)

The fault feature of rolling bearing in early failure period is difficult to extract. An incipient fault diagnosis method for rolling bearing based on parameter optimized variational mode decomposition method was proposed. Particle swarm optimization algorithm was used to search for the best combination of influencing parameters of variational mode decomposition algorithm, the penalty parameter and number of components were then set according to the searching results, and the fault signal was processed by parameter optimized variational mode decomposition algorithm. The original fault signal was decomposed into several intrinsic mode function components. The best signal component was selected and processed by envelope demodulation algorithm, the fault type of bearing was judged by analyzing the envelope spectrum of the signal. The simulated and measured signals of fault bearing were analyzed by parameter optimized variational mode decomposition method and the weak characteristic frequency information was extracted successfully. The results show that the proposed method enables to judge the incipient fault of rolling bearing effectively with desired reliability.

variational mode decomposition; particle swarm algorithm; rolling bearing; incipient fault diagnosis

2014-09-24。

唐贵基(1962—),男,博士,教授,博士生导师。

河北省自然科学基金资助项目(E2014502052)。

时间:2015-02-27

10.7652/xjtuxb201505012

TH17

A

0253-987X(2015)05-0073-09

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150227.0845.003.html