单元复习课选题指向：梳理，提升，建构——以“三角形”单元复习为例

☉江苏省如皋市下原镇下原初级中学 夏东方

单元复习课选题指向：梳理，提升，建构
——以“三角形”单元复习为例

☉江苏省如皋市下原镇下原初级中学 夏东方

单元复习，又称章节复习，是初中数学复习课的常见类型之一．这种复习主要分布在两个时段，一是单元新课结束之后，是新授知识结束时的即时性复习，还有就是在学期末综合复习之前，是迎接期终考试的终结性复习．这两个时段的单元复习课教学任务大致相同，主要是梳理单元中所学的知识，并将其与已学知识链接起来，形成系统化的知识网络．近期，笔者设计了一节单元复习课，复习的主题是人教版七年级下册的“三角形”，笔者以基础题组引领学生展开旧知梳理，通过适量的典型例题的训练与讲评巩固了旧知，实现了知识间的关联与融合，取得了较好的成效．本文就结合这节课谈谈单元复习课选题的三个选题指向：梳理，提升，建构，希望对您有所帮助．

一、梳理

单元复习课应有“复习味”，知识梳理应是课堂教学的主要任务．所以，我们为教学设计的任何形式的练习或例题，都应凸显出“复习主题”，力求通过这些题目的解答，唤醒学生脑海中“沉睡”的基础知识．显然，复习课例题与练习的设计应是教师在教学主线之上的精心之作，无论是题目的挑选与改编，还是题目的重组与整合，都应针对教学目标进行，力求使学生解题“有的放矢”．

案例1“三角形”复习题组设计——以题理知.

A．1B．2C．3D．4

（2）如图1，Rt△ABC中，∠ACB＝90°，CD为高，若∠ACD＝50°，则∠B的度数为（）.

A．50°B．40°

C．30°D．25°

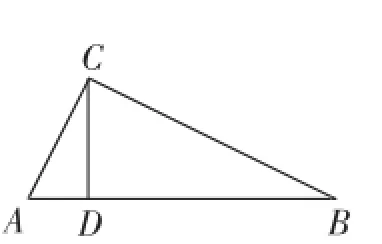
图1

（3）一多边形的内角和与其外角和相等，则这个多边形的边数为_________．

（4）如图2，△ABC的两条中线AM、BN相交于点O，已知△ABO的面积为4，△BOM的面积为2，则四边形MCNO的面积为_________．

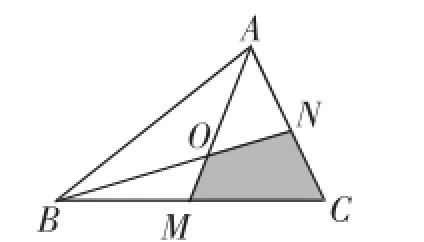
图2

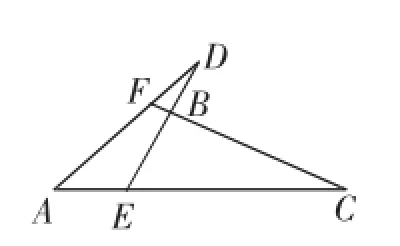
图3

（5）如图3，已知∠CBE=95°，∠A=28°，∠C=30°，求∠ADE的度数．

本文将专有知识成员定义为CPIKN中掌握专有知识的协同成员。协同成员pi是否为专有知识成员UKPi，本文使用布尔变量(pi,K)进行判定：如果协同成员pi是专有知识成员，则(pi,K)=1；反之(pi,K)=0。(pi,K)=0的判定规则如下：

教学设计：学生先独立完成“题组”，然后将解题结果和解题时用到的知识在小组中交流．交流结束后，教师组织学生在全班交流，重点交流各小组都出现错误的题目．

设计意图：我们首先来看题组，一共5个小题，从题型上看，选择、填空、解答都有，这与常规练习是一致的，符合学生的解题习惯．再来看看各小题的知识点的分布，第（1）题，指向了“三角形的三边关系”；第（2）题，指向了“三角形的高”和“直角三角形的两个锐角互余”；第（3）题，涉及的是“多边形的内角和与外角和”；第（4）题，是立足于“三角形的中线”性质之上的三角形面积问题；第（5）题，重点关注了“三角形的内角和定理”与“三角形的外角的性质”的应用．很明显，各个小题知识点的关联不大，一般都指向了“三角形”单元中的某一个或几个知识点，几乎没有出现重合或交叉．再来说说教学设计，教者在教学过程中将这5道题目同时呈现，要求学生先自主解答，然后在小组中交流“解题结果和解题时用到的知识”，最后再在全班交流“各小组都出现错误的题目”．很明显，学生的解题和交流都是以“以题理知”为目标的，从教学要求看，教师没有让学生纠结于解题思路的交流，而是侧重于结果与所用知识点的交流，交流“结果”避免了学生出现错误而不自知，交流用到的知识点重在“理知”，将所涉及的知识摆在“桌面上”“说清道明”．这样的题组及教学设计，学生是复习的主体，他们有解题过程的经历，知识的提取与应用的体验是深刻的，而小组与全班的交流，更是让那些潜藏在学生分析问题与解决问题过程中的知识暴露出来，为全体学生共同感知，“成为大家的知识”．

二、提升

在复习课上，练习是不可缺少的，但复习课不是练习课，我们绝不能以纯粹的练习代替讲评交流．复习课应在知识梳理的基础上进一步强化对这些知识的整合，将学生获得的知识有效地关联起来．在这些基础知识、基本技能、基本思想和基本活动经验的串联过程中，一些对今后问题解决适用的基本套路将会顺势形成，融入到学生的解题经验中．所以，对复习课而言，提升与梳理同样重要．为此，复习课也应设计一些推动旧知关联的提升题，在保证学生“吃得了”的同时，还要让学生“吃得饱”．这类提升题，一般是一些具有共性规律的问题，在交流中要突出共性方法的归纳与呈现．

案例2“三角形”复习题组设计——用知得法.

（1）等腰三角形中，一腰上的中线把三角形的周长分为12cm和15cm两部分，则此三角形的底边长为________．

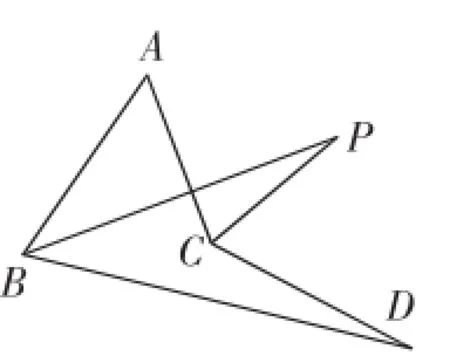
图4

（2）如图4，∠ABD，∠ACD的角平分线交于点P，∠A=50°，∠D=10°，求∠P的度数．

（3）如图5，线段AB、CD相交于点O，连接AD，CB．

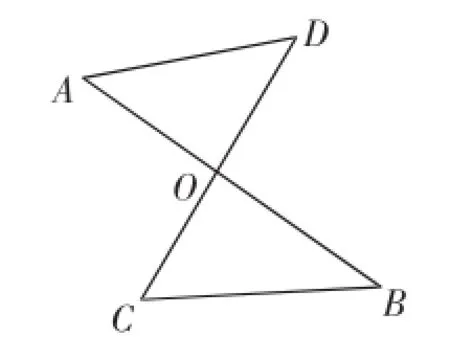
图5

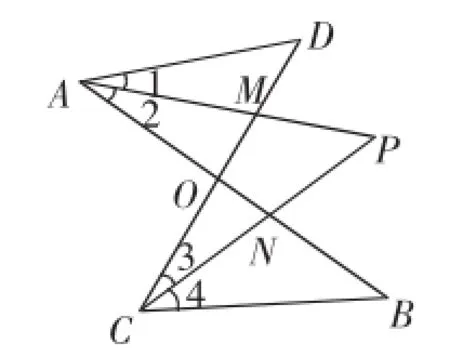
图6

①∠A、∠B、∠C、∠D之间的数量关系为________.

②如图6，在图5的基础上，作∠DAB和∠BCD的平分线AP、CP交于点P，AP与CD相交于点M，CP与AB相交于点N．若∠D=40°，∠B=30°，求∠P的度数.

③若图6中∠D和∠B为任意角，其他条件不变，请直接写出∠P与∠D、∠B之间的数量关系．

教学设计：学生先自主解答，教师巡视，请给出典型解题过程（既有正确的典型，又有错误的典型）的同学进行板演．待全体学生解答结束后，教师组织学生在小组中交流，重点交流分析过程和解题过程．最后，教师结合黑板上学生展示的典型过程进行讲评，让学生发现其中的亮点和不足，并尝试归纳出解题的一般规律和规避典型错误的策略．

设计意图：提升是复习课的重要任务，在学生借助基础题组完成知识扫描之后，用以提升的典型例题就应“登台唱戏”了．这里的3道题目是教者从众多的与三角形有关的考题中挑选出来的．第（1）题，将三角形的中线、三边关系、等腰三角形和分类讨论思想等结合在一起，是“三角形中的重要线段”的典型例题，综合程度较高；第（2）题，将角平分线、三角形的内角和、三角形的外角和及整体思想结合起来，融合了“与三角形有关的角”的很多重要知识，难度不小；第（3）题，涉及了三角形的内角和、三角形的外角、角平分线、整体思想和特殊一般的思想，知识点更加丰富，能否从图6中提取出图5给出的基本图形直接影响着解题的成效．根据这里的分析，三道题目不仅涉及了三角形中的重要线段和重要的角，还用到了很多初中阶段的重要数学思想．几道例题将本单元的核心知识与初中阶段涉及的重要数学思想关联在一起，题目有较强的代表性，此时的问题解决已不再是仅仅停留在基础知识的简单应用上，一些常用的解题套路在学生分析求解、互动交流与教师的点评提升过程中会自然生成，成为所有人的共识．如果能在后续解题训练中将得到的这些“共识”进一步强化，这些符合学生解题需求的“套路”在学生的知识网络中“扎根”是迟早的事！

三、建构

知识网络是隐形的，它悄悄地潜藏在学生的脑海之中．在学生的认知过程中，知识网络的建构历程并不像求解题目那样直观，也不似学生交流那样直白，网络的建构过程一般都是隐形的，知识在应用交流与反思中慢慢地融合在一过．要想让这些知识网络化显性出现，我们可以在学生的解题与交流之中，借助板书或投影将知识间的“链接点”部分展示，给学生以直观的认知．这种基于知识梳理之上的展示，给学生的是视觉的刺激，激活的是他们的创造性思维，推动了知识的融合和网络的建构．在教学中，我们应高度重视用板书或投影的方式进行知识链的展示，用好传统教学媒体和新媒体，恰到好处地将知识“织成网络”，为后续学习与应用形成有效的思维链，从而大幅度地提升学生分析问题和解决问题的能力．

案例3“三角形”单元复习课的教学流程.

活动一：自主解答，以题理知．

活动过程：学生自主解答题组1，小组交流，然后教师组织学生全班交流，梳理“三角形”单元的基础知识．在此过程中，教师将学生在全班交流时陈述的知识点进行了板书（如图7，下同），并根据预设进行了必要的补充．

活动二：典例讲评，用知得法．

活动过程：根据上面的教学设计，学生先后经历了自主解答题组2，然后分别在组内和全班进行了交流．教师在学生组内和全班交流过程中，对解题用到的本单元的基础知识及与解题有关的数学思想方法进行了补充板书．

活动三：整理反思，小结提升．

活动过程：请学生在小组中交流各自的收获和困惑，3分钟后，教师让学生在全班分享各自的学习成果．在学生陈述过程中，教师逐步充实板书，形成板书终稿，如图7．

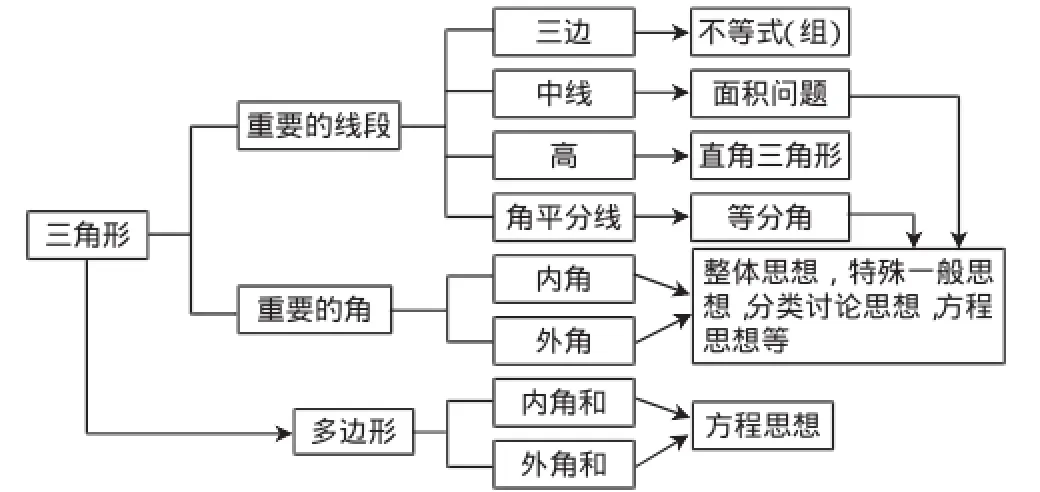
图7

简析：复习课，练习做得多，师生互动多，但能给学生留下的未必多．单元复习涉及的知识都是学生已经学过的，如果就题目讲知识，那就是“炒冷饭”，就是不断重复“过去的故事”，复习的意义也就失去了．从教学追求看，单元复习的最大价值在于将这一单元的知识与旧知有效关联起来，使单元知识融入知识网络中去，成为知识系统的一部分．板书或投影是课堂教学的重要组成部分，适时地板书或投影将能让知识的关联显性化，让原本在学生脑海中的关联变为“文本”、“箭头”、“连线”，以直观方式实现形象串联．板书或投影应如案例中那样，贯穿于教学始终，从第一个活动“知识梳理”就已经展开，到最后的课堂小结精准“收尾”．最终，呈现出来的应是一幅有文字、有连线，整体性很强的框图，必要时，我们还可以让符号、图形、表格等信息载体参与到知识的网络化建构中来，让知识间的衔接方式更加多样化，让我们的知识结构更为丰富，从而适应不同学生的认知需求．

单元复习课的入口小，所要复习的仅为单元内获得的知识，通常应紧扣主题单元展开．但是，单元复习的出口应该是宽阔的，无论是即时性复习，还是终结性复习，都不能就单元复习单元，我们应将单元复习置于整个阶段或整个学段的层面上进行设计，站在“全局”的角度设计单元复习课的教学目标，并在目标的指引下选题，指向“梳理，提升，建构”，让单元复习课具有浓浓的“复习味”，力求以一课之力实现单元复习课的教学价值，为学生的数学素养的提升“添砖加瓦”！

1．印冬建．突出核心主线追求有效教学——谈初中数学有效备课的做法和思考［J］．中学数学（下），2014（1）．

2．万茂绪．以题理知：回顾概念的有效方法——两则教学案例的对比分析及感悟［J］．中学数学（下），2014（11）．Z