钻芯法检测坝工实体混凝土抗冻性能研究

闪 黎杨 智（.淮河水利委员会治淮工程建设局 蚌埠 233000 2.安徽省·水利部淮委水利科学研究院蚌埠 233000 3.安徽省水利工程病害防治工程技术研究中心 蚌埠 233000）

钻芯法检测坝工实体混凝土抗冻性能研究

闪 黎1杨 智2,3
（1.淮河水利委员会治淮工程建设局 蚌埠 233000 2.安徽省·水利部淮委水利科学研究院蚌埠 233000 3.安徽省水利工程病害防治工程技术研究中心 蚌埠 233000）

我国的坝工建筑物主要分布在山区及丘陵地带，昼夜温差大，一般对混凝土抗冻性能有较高的要求，尤其是高纬度或者高海拔地区；混凝土的抗冻性能作为混凝土耐久性设计的重要参数，被行业内广泛关注。目前，在混凝土冻融破坏机理研究、如何提高混凝土抗冻性能等方面取得了重大突破，然而在坝工实体结构混凝土抗冻性能现场检测领域少有人问津。为此，笔者通过大量试验研究，拟合了混凝土芯样抗冻性能参数与标准棱柱体抗冻性能参数的相关关系曲线，提出或可通过对坝工实体结构钻芯取样，获取芯样的抗冻性能参数，依据函数预测标准棱柱体的抗冻性能参数，从而参照现行标准确定坝工混凝土抗冻等级的现场检测方法。

坝工实体 钻芯法 抗冻性能 现场检测

目前，为了提高混凝土的抗冻性能，通常向混凝土中掺入引气剂或引气减水剂，引气剂的掺入能使混凝土在拌和过程中引入大量微小、封闭的气泡，引气的目的是为混凝土提供足够气泡数量，以增加内部逃逸边界，以改善混凝土的和易性和耐久性。通常将掺入引气剂的混凝土称为引气混凝土，或有抗冻融指标要求时也称作抗冻混凝土。随着混凝土新工艺辈出，商品混凝土的发展成熟与广泛应用，因而课题组着重于对商品混凝土抗冻性能的研究，试验阶段主要采用二级配混凝土。

1 试验设计

实验室分别预制强度等级为C25、C30、C35、C40的引气混凝土，引气剂型号为WDSP型高效减水引气剂，掺入量为2.0%，以覆盖坝工常用的混凝土等级。成型尺寸为30cm×40cm×50cm的立方体试块各3块，自然养护90d，用于模拟坝工实体构件，养护时间28d后，采用矩阵工程钻机分别从每个试块上钻取2个直径为100mm、长度为400mm的圆柱形芯样，对芯样进行标准养护；同时预留标准棱柱体试件各1组，标准养护90d。将一半数量的芯样与对应的标准棱柱体试件在到达试验龄期的前4d，于20± 3℃温水中浸泡4d。

90d龄期后，将未泡水的一半数量芯样用于抗压试验，确定混凝土强度等级，泡水构件进行冻融试验，分别进行25次、50次……200次冻融循环，并记录相关抗冻性能参数。

2 芯样试件与标准试件抗冻性能分析

2.1 质量损失率

2.1.1 C25标准试件质量损失率与芯样试件质量损失率相关关系

根据标准试件质量损失率与芯样试件质量损失率散点分布形式，分别采用线性、二次型曲线拟合其相关关系，曲线拟合及方差分析均采用SPSS统计分析软件进行，成果见表1、表2。

因变量为标准试件质量损失率，自变量为芯样试件质量损失率，散点图形见图1。

曲线选型：二次曲线相关系数为0.999，估计值的标准误为0.023，明显优于线性曲线，函数关系式为：

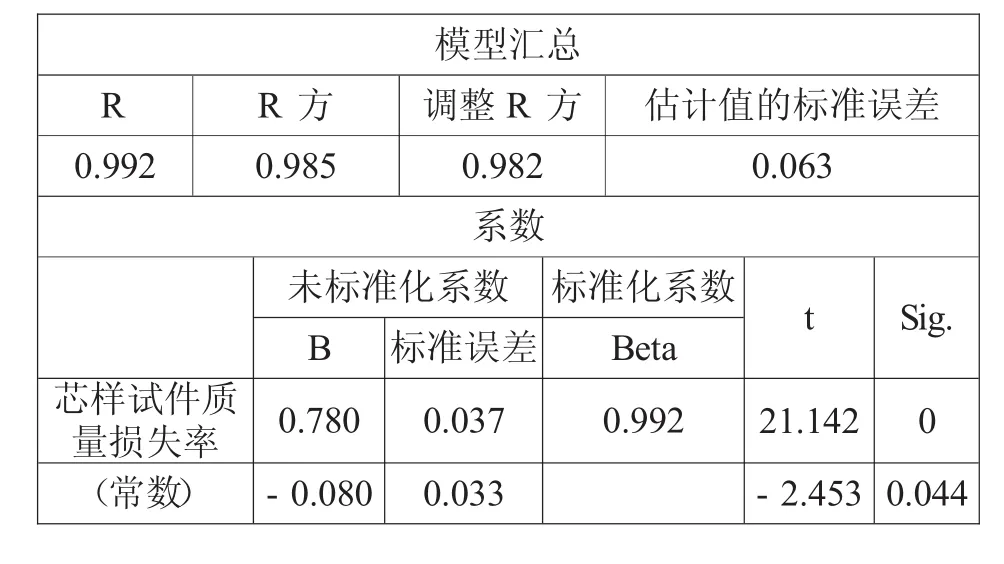
表1 线性函数

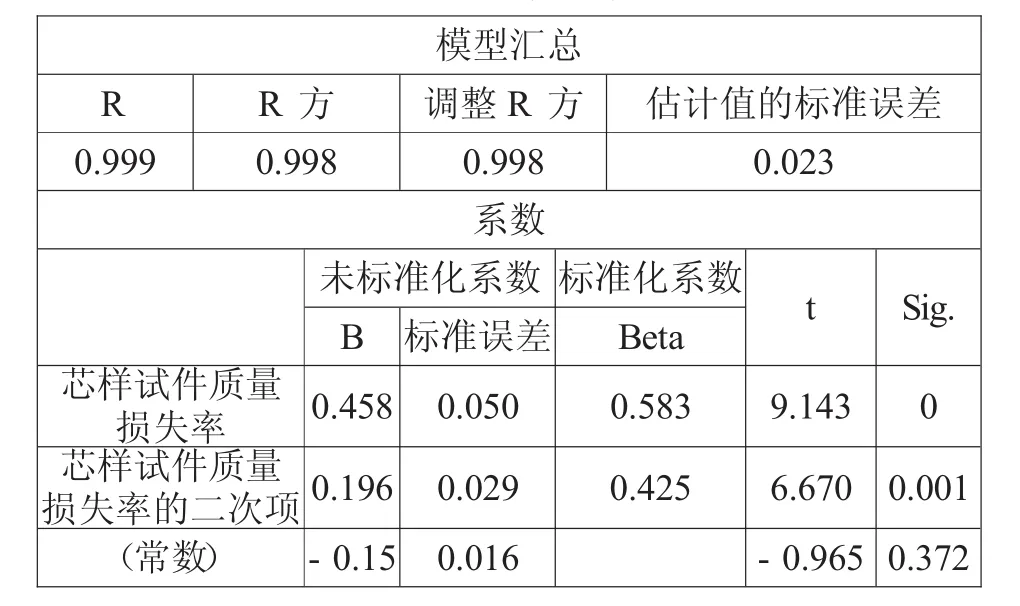
表2 二次函数

图1 C25标准试件质量损失率与芯样试件损失率相关关系曲线

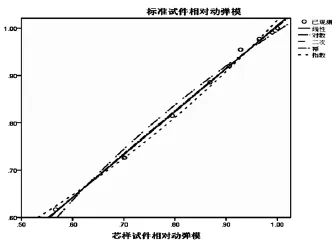
图2 C25标准试件相对动弹模与芯样试件相对动弹模相关关系曲线

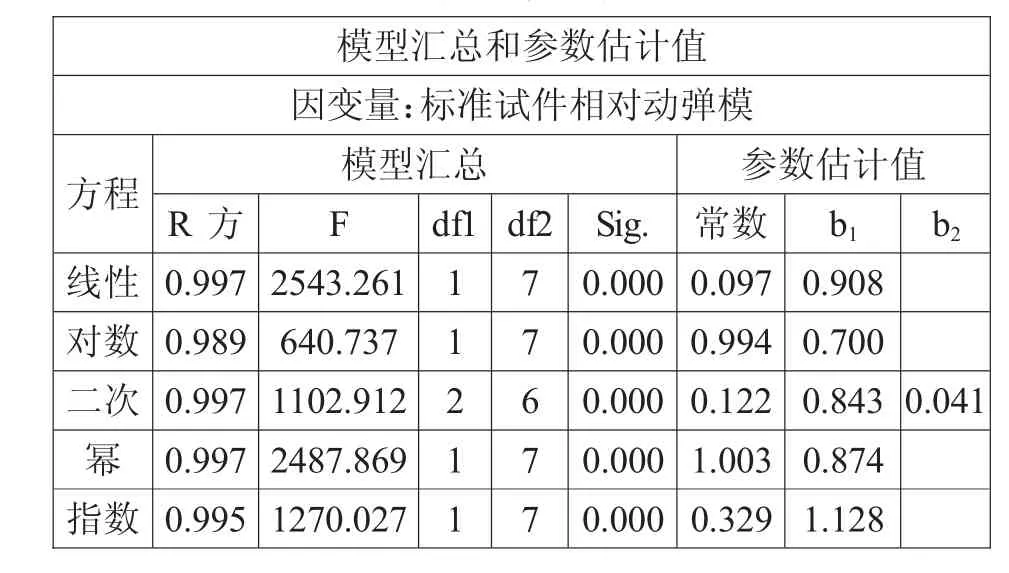
表3 5种曲线形式拟合比对

ΔmL=0.196ΔmX2+0.458ΔmX-0.015

式中：ΔmL—标准试件质量损失率，%；ΔmX—芯样试件质量损失率，%。

2.1.2 C30标准试件质量损失率与芯样试件质量损失率相关关系

为避免冗余，仅给出分析结果，过程数据及散点分布图不再列出。

曲线选型：二次曲线相关系数为0.999，估计值的标准误为0.014，明显优于线性曲线，函数关系式为：

ΔmL=-0.074ΔmX2+0.964ΔmX-0.007

2.1.3 C35标准试件质量损失率与芯样试件质量损失率相关关系

曲线选型：二次曲线相关系数趋近于1.0，估计值的标准误为0.008，明显优于线性曲线，函数关系式为：

ΔmL=-0.136ΔmX2+0.913ΔmX-0.002

2.1.4 C40标准试件质量损失率与芯样试件质量损失率相关关系

曲线选型：线性曲线相关系数趋近于1.0，估计值的标准误为0.004，略优于二次曲线，函数关系式为：

ΔmL=0.784ΔmX

2.1.5 不同强度等级标准试件与芯样试件质量损失率比对分析

随着强度等级的提高，标准试件与芯样试件质量损失率的相关关系曲线逐渐由二次型转变为线性，强度等级越高，标准试件与芯样试件质量损失率的相关关系越趋近于线性。

2.2 相对动弹模

2.2.1 C25标准试件相对动弹模与芯样试件相对动弹模相关关系

根据散点分布形式，分别选取线性、对数、二次型、幂、指数函数5种线型拟合标准试件相对动弹模与芯样试件相对动弹模间的相关关系（见表3），5种曲线Sig.值均小于0.05，说明相关关系均显著，比对5种线型的R方值和卡方值F，择优选取两者数值较大的曲线形式，线性曲线和幂函数曲线拟合度明显优于其他3种线型，线性函数卡方值更大，因而择优选取线性函数，表达式如下：

ΔEL=0.908ΔEX+0.097

式中：ΔEL—标准试件相对动弹模；ΔEX—芯样试件相对动弹模。

曲线R方值为0.997。散点图形见图2。

2.2.2 C30标准试件相对动弹模与芯样试件相对动弹模相关关系

同上，不再列出曲线系数表及散点分布图。5种曲线Sig.值均小于0.05，说明相关关系均显著；比对5种线型的R方值和卡方值F，择优选取两者数值较大的曲线形式，线性曲线和幂函数曲线拟合度明显优于其他3种线型，幂函数卡方值更大，因而择优选取幂函数，表达式如下：

ΔEL=1.002ΔEX0.874

曲线R方值为0.997。

2.2.3 C35标准试件相对动弹模与芯样试件相对动弹模相关关系

5种曲线Sig.值均小于0.05，说明相关关系均显著；比对5种线型的R方值和卡方值F，择优选取两者数值较大的曲线形式，对数函数曲线和幂函数曲线拟合度明显优于其他3种线型，对数函数R方值和卡方值更大，因而择优选取对数函数，表达式如下：

ΔEL=1.002log0.703ΔEX

曲线R方值为0.995。

2.2.4 C40标准试件相对动弹模与芯样试件相对动弹模相关关系

5种曲线Sig.值均小于0.05，说明相关关系均显著；比对5种线型的R方值和卡方值F，择优选取两者数值较大的曲线形式，对数函数曲线和幂函数曲线拟合度明显优于其他3种线型，对数函数卡方值更大，因而择优选取对数函数，表达式如下：

ΔEL=0.997log0.677ΔEX曲线R方值为0.997。

2.2.5 不同强度等级标准试件与芯样试件相对动弹模比对分析

随着强度等级的提高，标准试件与芯样试件质量损失率的相关关系曲线逐渐由线性转变为对数函数形式，强度等级越高，标准试件与芯样试件质量损失率的相关关系越趋近于对数函数。

3 结语

（1）同条件的芯样的抗冻性能参数和标准试件的抗冻性能参数间的相关关系在误差允许的范围内可以量化，且随着强度等级的提高，标准试件与芯样试件质量损失率的相关关系曲线逐渐由二次型转变为线性，强度等级越高，标准试件与芯样试件质量损失率的相关关系越趋近于线性；标准试件与芯样试件质量损失率的相关关系曲线逐渐由线性转变为对数函数形式，强度等级越高，标准试件与芯样试件质量损失率的相关关系越趋近于对数函数。

（2）课题组采用成型大试件自然养护以模拟坝工实体构件，并预留同批次混凝土的标准试件，通过获取芯样抗冻性能参数值，探索得到了与标准试件抗冻参数值间相关关系曲线，该项研究成果使得今后进一步发展坝工混凝土构件抗冻性能的现场检测技术成为可能。

（3）课题组大量研究成果均是基于常规普通引气混凝土，对于特种混凝土及高强混凝土的芯样抗冻性能试验研究尚需进一步拓展