旋转降落伞系统角运动及稳定性分析

马晓冬，郭 锐，刘荣忠，吕胜涛

（南京理工大学 智能弹药技术国防重点实验室，南京210094）

旋转伞是一类具有非轴对称结构的降落伞，充满时伞衣形成与旋转方向一致的排气口。旋转伞在空中下落时，流入伞衣的气流从排气口排出，产生的反作用力矩使伞衣绕伞轴旋转。伞衣的高速旋转使带旋转伞的伞物系统下降时具有良好的稳定性［1］。随着兵器技术、航空航天技术的飞速发展，旋转伞作为气动力减速器得到了广泛应用，如末敏子弹的减速导旋主伞［2］等。

作为重要的减速装置，降落伞具有良好的运动稳定性是其可靠工作的必要条件，所以伞物系统的稳定性研究十分重要。文献［3－4］通过理论建模，对运动方程线性化处理，给出了物伞系统平面运动的稳定性判据。文献［5］建立了伞舱系统刚性连接和弹性连接时的数学模型，分析了降落伞侧向力系数、吊带长度、降落伞和载荷质量比及吊带性质对系统运动稳定性的影响。可发现，已有运动稳定性研究多关注结构轴对称的降落伞，对旋转伞运动稳定性的研究甚少。虽然文献［1］指出旋转伞由于高速旋转而具有良好的稳定性，但其运动稳定性的相关规律还有待探索。

为了了解旋转伞的运动稳定性，本文从理论建模出发，建立旋转伞－载物系统角运动的数学模型，研究系统主要参数对运动稳定性的影响。

1 旋转降落伞系统运动方程

1.1 基本假设

旋转伞系统简图如图1所示。处于平衡状态的旋转伞系统受到小扰动时，旋转伞的充满形状及其与载物间的相对位置不发生明显变化，故运动稳定性分析时，采用如下假设：

①旋转伞和载物均为刚体，且二者刚性连接。②只考虑旋转伞的空气动力，气动力参数为常数，旋转伞的压心与质心位置重合。③载物为一圆柱体，其轴线与伞轴重合。④不考虑风的影响。

图1 伞弹系统结构简图

1.2 坐标系

地面坐标系O0xyz，原点为初始时刻系统质心在地面的投影，O0x轴沿水平线指向系统运动方向，O0y轴竖直向上，O0z轴按右手法则确定。

速度坐标系Ox2y2z2，O为系统质心，Ox2轴沿系统质心速度矢量v的方向，Oy2轴垂直于速度向上，Oz2轴按右手法则确定。其相对于O0xyz的方位由速度高低角θa和速度方位角ψ2确定，转动角速度为

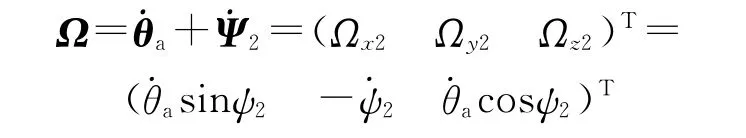
伞轴坐标系Oξηζ，Oξ为伞轴，Oη轴垂直于伞轴向上，Oζ按右手法则确定。其相对于O0xyz的方位由伞轴高低角φa和伞轴方位角φ2确定，转动角速度为

在伞轴坐标系中，系统相对于伞轴Oξ的自转角为γ，则系统的总角速度为

速度坐标系到伞轴坐标系的转换矩阵为

式中：δ1为高低攻角，δ2为方向攻角。则旋转伞质心速度在速度坐标系中的投影为

式中：Lp为旋转伞质心位置向量，在伞轴坐标系中Lp＝（－lp0 0）T。

1.3 受力分析

系统所受外力包括旋转伞空气阻力、升力、重力和载物重力，外力矩包括旋转伞导旋力矩、极阻尼力矩、赤道阻尼力矩和外力产生的力矩。

将系统外力向速度坐标系投影。旋转伞空气阻力和升力分别为

式中：ρ为空气密度，S为旋转伞特征面积，Cx为旋转伞阻力系数，C′y为旋转伞升力系数导数，I为伞轴方向单位向量。

系统重力为

式中：mp、mb和ma分别为旋转伞质量、载物质量和伞附加质量。

力矩在伞轴坐标系中表示。导旋力矩为

式中：l为旋转伞特征长度，mxw为导旋力矩系数。极阻尼力矩为

式中：m′xz为旋转伞极阻尼力矩系数导数，d为特征直径。

赤道阻尼力矩为

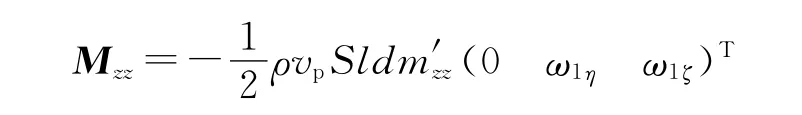
式中：m′zz为旋转伞赤道阻尼力矩系数导数。

旋转伞阻力、升力及伞物的重力对系统质心的合力矩为

载物质心矢量在伞轴坐标系中表示为Lb＝（lb0 0）T。

1.4 运动方程

1.4.1 系统质心运动方程

地面坐标系中，根据质心运动定理，旋转伞系统质心的运动方程为

向速度坐标系Ox2y2z2上投影，由于v，则质心运动方程为

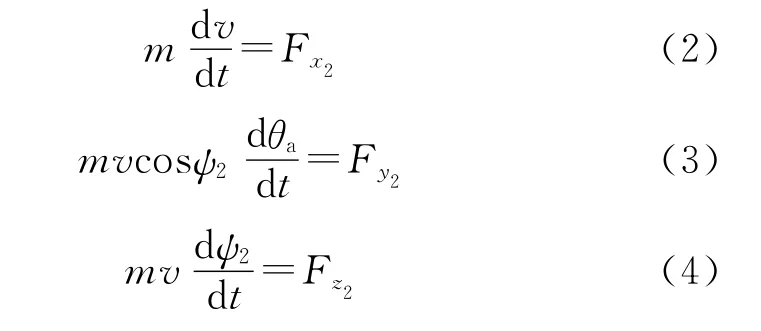
1.4.2 系统转动方程

根据动量矩定理，旋转伞系统绕质心的转动方程为

式中：J为系统的转动惯量矩阵，在伞轴坐标系中，有：

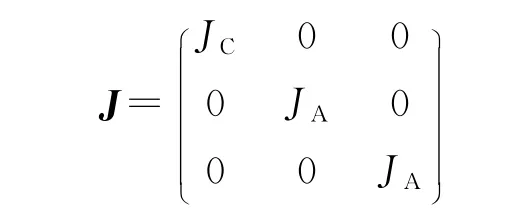
式中：JA为系统赤道转动惯量，JC为极转动惯量。

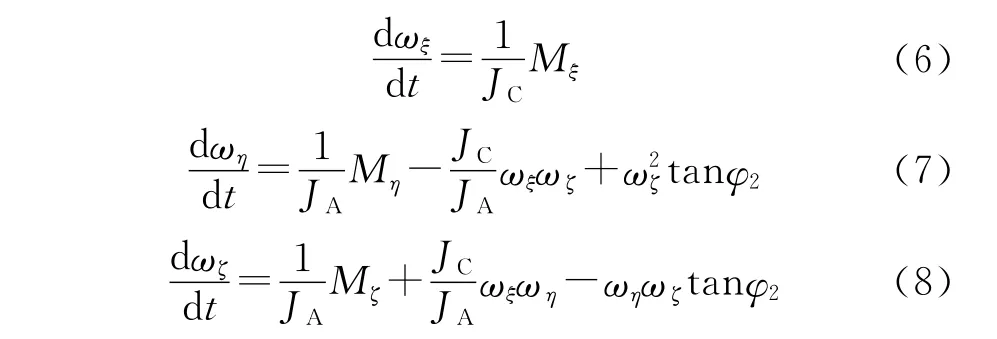
2 角运动方程的建立

用复摆动角Φ和复偏角Ψ来描述旋转伞系统的角运动［6］，其中：

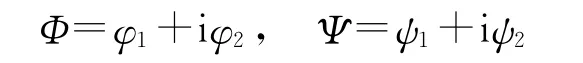
设θi为理想弹道倾角，即理想弹道的速度方向与基准坐标系O0x的夹角，因为旋转伞系统理想弹道的速度方向为竖直向下，所以θi＝－90°。小扰动时，扰动弹道接近理想弹道，令θa＝θi＋ψ1＝－90°＋ψ1，φa＝θi＋φ1＝－90°＋φ1。φ1，φ2，ψ1，ψ2，δ1，δ2均是小量。

引入符号：

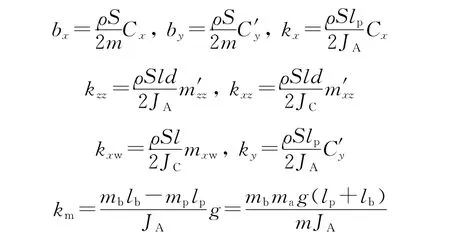
2.1 复偏角方程

当伞物系统在平衡位置附近时，假设1和2为小量，将受到的外力代入式（3）和式（4），略去高阶小量，得：

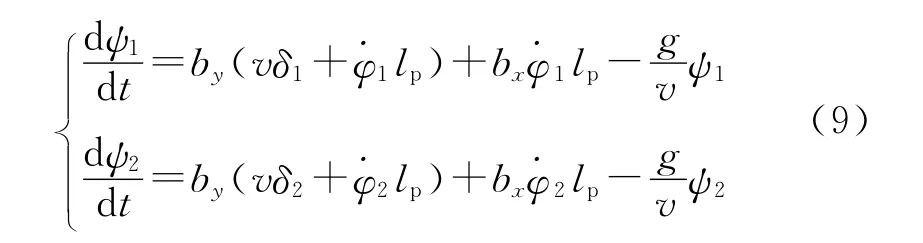
第二式乘以i与第一式相加得复偏角方程：

式中：Δ＝δ1＋iδ2为伞系统复攻角。

由于

式中：X为任意变量，s为弧长。故可将式（10）的自变量从时间改为弧长：

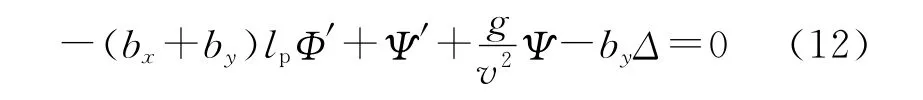
2.2 复摆动方程

旋转伞自转角速度一般为3～6r／s，远大于横向摆动角ωζ，且tanφ2为小量，故ωξ≈。在平衡位置附近时，／dt＝0，得

将系统受到的力矩及ωζ≈＝、ωη＝－代入式（7）和式（8），并略去高阶小量，得：

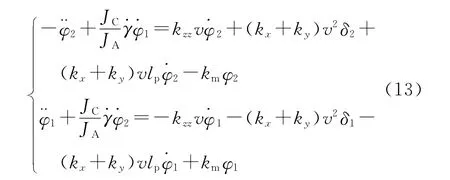
将第一式乘以（－i）与第二式相加，得复摆动角方程：

利用式（11），将式（14）转化为

3 角运动及稳定性

3.1 角运动分析

将Δ＝Φ－Ψ代入式（12）和式（15），得：

取系统主要参数：Cx＝1.1，lp／lb＝1.2，C′y＝0.03，m′zz＝0.02，mxw＝1，m′xz＝0.3，mp／mb分别取0.15 和 0.25，系统初始扰动：Φ0＝0.7°ei30°＝0.61°＋i0.35°，Φ′0＝0，Ψ0＝0.5°ei30°＝0.43°＋i0.25°。

图2为给定系统参数下的攻角变化情况。mp／mb＝0.15时，δ1和δ2约在s＝20m 处衰减至0，旋转伞系统较迅速地达到平衡位置Δ＝0，复攻角变化情况如图3所示。mp／mb＝0.25时，δ1和δ2在平衡状态附近震荡变化，振幅有变大的趋势，复攻角不会达到平衡位置，系统不稳定。继续增大mp／mb，δ1和δ2发散速率增大，伞系统最终发生翻滚。

可见，系统参数影响着旋转伞系统的角运动。欲使旋转伞系统具有良好的运动稳定性，受到初始扰动时其角运动能很快地衰减至0，需掌握系统参数对系统角运动的影响规律。

图2 系统攻角变化

图3 复攻角变化

3.2 系统参数对稳定性的影响

系统的平衡位置为Φ＝0，Ψ＝0，则方程组（16）即系统角运动扰动方程，其特征方程为

式中：

欲使旋转伞系统稳定，扰动方程的特征根必须都具有负的实部。由于特征方程系数含有虚数，稳定性判据的理论求解困难，故对特征方程（17）进行数值求解，得到特征根。对于具有运动稳定性的系统，扰动衰减至0的速率主要取决于特征值最大实部λp的数值大小。λp＜0，且其它参数一定时，｜λp｜越大，扰动衰减越快，则系统稳定性越好。

图4给出旋转伞阻力系数和导旋力矩系数对λp的影响。当Cx＜2.0时，λp为负值，说明在选定系统参数下，旋转伞系统具有运动稳定性。随着Cx的增大，｜λp｜先增大后减小，在Cx＝1.0附近取极值｜λp｜max。当Cx较小时（本例中小于1.0），mxw对λp无明显影响。在Cx＝1.0附近时，mxw越大，即系统的稳定转速越高，｜λp｜max越小，λp变化越平缓。特别地，当mxw＝0时，｜λp｜max最大，但这并不是说明转速越高，系统稳定性越差。因为旋转降落伞的阻力系数要比其他一般非旋转伞要高，如涡环旋转伞的阻力系数为0.95～1.55，而一般非旋转伞的阻力系数只有0.3～0.9［1，7］，所以通过调整设计旋转伞的结构，可较容易地使Cx落在极值位置的附近，进而使系统扰动衰减速率大于非旋转伞。当Cx很大时（大于极值点），mxw越大，｜λp｜越小，但大部分降落伞的阻力系数达不到如此大的数值。所以，与非旋转伞相比，旋转伞具有更好的运动稳定性，而且在旋转伞阻力系数变化范围内，转速越高，｜λp｜变化越平缓，即稳定性受阻力系数的影响越小。

图4 λp与mxw的关系

图5 为旋转伞特征长度与直径关系对λp的影响。可看出，增大l／d，｜λp｜max减小，相对应的Cx也减小，且减小幅度很大。所以，当旋转伞阻力系数较小时，应增大旋转伞特征长度；当旋转伞阻力系数较大时，应尽量减小其特征长度。

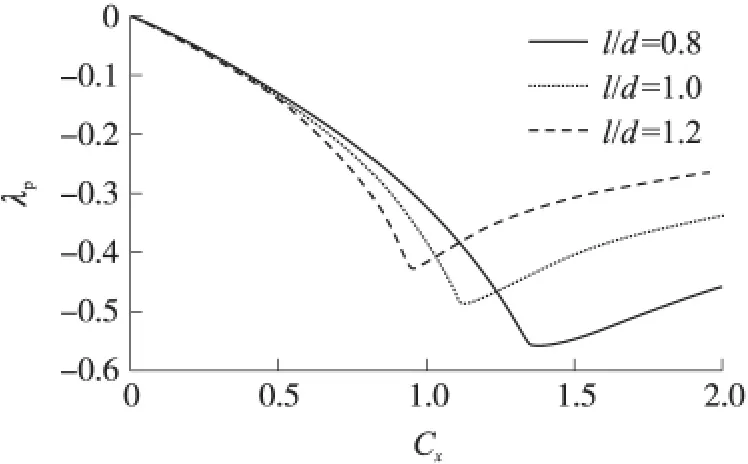
图5 λp与l／d的关系

图6 给出旋转伞与载物质量关系对λp的影响。减小mp／mb，｜λp｜max先增大后减小，且相对应的Cx增大。当mp／mb很小时（如小于0.05），λp始终为负值，系统具有运动稳定性，但｜λp｜max对应的Cx大于旋转伞阻力系数的变化范围，故系统扰动衰减较慢。当mp／mb很大时（如小于0.15），｜λp｜相对较小，系统稳定性较差。继续增大mp／mb（如等于0.25），在Cx＝1附近，λp将变为正值，系统不具备运动稳定性。所以，对于结构确定的旋转伞，可通过调节载物质量，使｜λp｜max与旋转伞的Cx正好对应，从而运动稳定性达到最优。

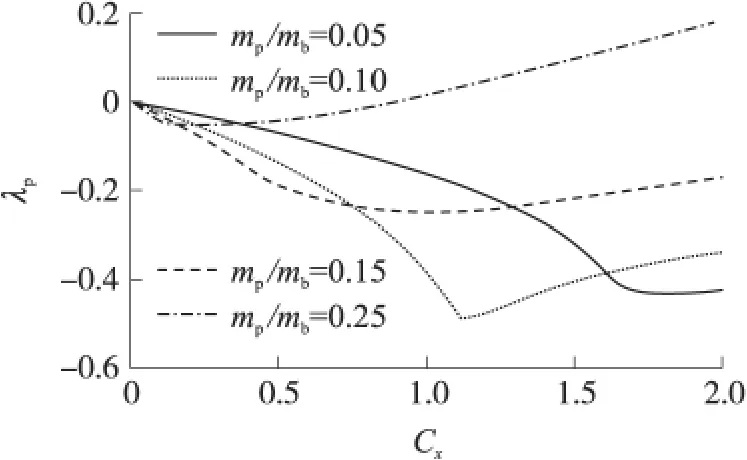
图6 λp与mp／mb的关系

4 结论

本文基于经典弹道方程，在小扰动的条件下，建立旋转伞系统的复偏角方程和复摆动角方程，通过角运动扰动方程的特征值研究系统的运动稳定性。

①旋转降落伞的运动稳定性优于结构轴对称的非旋转降落伞，转速越高，旋转伞系统稳定性受阻力系数影响越小。

②为提高系统扰动衰减速率，当旋转伞阻力系数较小时，应增大旋转伞特征长度；当旋转伞阻力系数较大时，应尽量减小其特征长度。

③相对于旋转伞，载物质量过大时，系统总是稳定的，但系统受到扰动后达到稳定状态时间长；载物质量过小时，系统出现不稳定现象；实际应用中，要选取合适的旋转伞和载物质量，使系统在较短的时间内达到稳定状态。

④旋转伞系统运动稳定性的好坏与旋转伞阻力系数关系密切。在设计及应用中，可根据旋转伞阻力系数设定系统其他参数，使旋转伞系统具有良好的运动稳定性。

［1］王利荣.降落伞理论与应用［M］.北京：中国宇航出版社，1997.WANG Li－rong.Theory and application of parachute［M］.Beijing：China Astronautic Publishing House，1997.（in Chinese）

［2］王国平，芮筱亭，张弛，等.远程火箭末敏弹弹道特性仿真［J］.弹道学报，2011，23（4）：1－4.WANG Guo－ping，RUI Xiao－ting，ZHANG Chi，et al.Simulation of ballistic characteristics of long－range－rocket target－sensitivity－projectile［J］.Journal of Ballistics，2011，23（4）：1－4.（in Chinese）

［3］李大耀，李大治.物－伞系统运动方程与稳定性判据［J］.中国空间科学技术学报，1994，15（1）：8－17.LI Da－yao，LI Da－zhi.Motion equations and stability criteria of body－parachute system［J］.Chinese Space Science and Technology，1994，15（1）：8－17.（in Chinese）

［4］李大耀，李大治.物－双伞系统运动方程与稳定性判据［J］.宇航学报，1997，18（4）：93－97.LI Da－yao，LI Da－zhi.Motion equations and stability criteria of body－parachutes system［J］.Chinese Space Science and Technology，1997，18（4）：93－97.（in Chinese）

［5］王海涛，郭叔伟，秦子增.降落伞特性对伞舱系统运动稳定性的影响［J］.航天器工程，2009，18（2）：68－73.WANG Hai－tao，GUO Shu－wei，QIN Zi－zeng.Influence of character of parachute on stability of parachute－cabin system［J］.Spacecraft，2009，18（2）：68－73.（in Chinese）

［6］韩子鹏.弹箭外弹道学［M］.北京：北京理工大学出版社，2008.HAN Zi－peng.Exterior ballistics of projectile and rocket［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）