应急物资储备点选址问题研究

郭继坤 穆祥静，2

(1.后勤工程学院，重庆401311;2.海军工程大学 勤务学院，天津300450)

1 引言

应急物资储备点选址是应急物资储备布局优化需解决的关键问题，即在现有物资储备点地址的基础上，根据可能担负的任务、地形交通状况、储存条件和资源配置等因素，科学确定或调整物资的储备布局，为国家物资储备建设和处理突发事件提供更加有效的物资供应。

关于应急物资储备点选址问题研究，军内专家多次展开相关研究:如张来顺采用运筹学中动态规划的方法建立数学规划模型，并采用模型分解与启发式算法相结合的方法求解［1］;陈阳提出将物联网技术应用到应急物资储备布局的观点［2］;陈智提出在考虑运输方式和道路换乘的条件下，对实际运距进行标准运距的换算，以达到不同运送方式下保障时效的可比性，选出布局优化方案［3］;双海军引入计算机SLAM 仿真技术和综合评判方法对储备布局进行优化研究［4］;徐东提出建立构建军事物资储备布局评价、调整模型的思路，使得物资储备布局可随军事战略方针和兵力部署的变化而及时、合理地调整［5］。从以往研究结果看，应急物资储备点选址问题是一种典型的多目标优化问题，不同学者因目标设定不同和采用方法各异而得出不同的研究结论。

本文采用多目标决策方法对应急物资储备点选址问题展开研究，与以往研究方法相比较，该方法的创新之处在于:综合考虑多种影响因素，使优化结果更符合选址实际需求，并且为规避各目标之间存在的矛盾，首先结合军用标准地图提供的道路信息，确定各目标的影响因素;其次运用模糊层次分析法，对最“底层”影响要素结合专家打分或经验取值构造优先关系矩阵，从而确定上级目标的权重系数;最后再对选址问题进行目标决策，使得结果最优。

2 确定应急物资储备点选址目标

2.1 距离最短

储备点至最远需求点的距离在满足物资保障要求的前提下，越短越优。如:应急物资储备点距前方为150—200 公里，在此范围内前送距离越短越好，优化目标是找出距需求点距离最短的储备点。

2.2 时间最短

储备点到最远需求点的时间在满足最短时间要求的前提下，时间越短越好。如果存在多点储备，同时多点保障的情况，优化目标是找出到需求点时间最少的储备点。

2.3 调运成本最少

储备点到各需求点的总调运成本最少，即物资输送的总吨公里数最小。这一目标主要针对平时物资供应管理，达到节约目的。

2.4 储备点建设成本最低

应急物资储备点建设成本主要指建设的地理费用，包括建筑物、设备、土地和运输距离等相关费用。此项费用与储备点的地理位置和规模有关。

2.5 储备数量在满足持续消耗需求的前提下最低

储备点应急物资储备数量满足规定时限内的持续消耗要求，多则浪费，少则不能达到保障要求。

3 确立备选应急物资储备点

应急物资储备点选址的实施，重点是确立备选应急物资储备点。备选应急物资储备点的确立需要考虑储备点的储存条件、交通状况、安全情况和补充的难易度等因素，并不是所有能建立物资库站的位置都能成为储备备选点。

3.1 根据任务确定储备备选点

根据不同任务以及物资来源的情况，选择储备备选点。备选点的选取对最优方案和计算求解的过程以及运算成本有着直接的影响。备选点过多，会使模型复杂化，计算工作量剧增;而备选点太少，则可能使所得优化方案偏离最优解太远，达不到合理布局的目的。

3.2 对各备选点进行综合评价

确定了应急物资储备备选点，就要对每个备选点进行具体分析和综合评价，从整体保障效益的角度出发，权衡该备选点在布局中作用的大小。评价的指标有:①储存条件，包括水源、地幅、地势、坡度等;②交通条件，包括附近铁路、公路状况，通行程度等;③地形隐蔽条件，包括疏散地域、地表覆盖情况等;④靠近物资需求点，包括标准运距、实际距离、到达时间;⑤靠近物资供应点，包括实际距离，运送时间。

设有A1，A2，…，Am是评价方案的m个替代方案，x1，x2，…，xn是评价替代方案的n个评价指标，w1，w2，…，wn是n个评价指标的权重，vi1，vi2，…，vin是第i个替代方案Ai的关于xj指标(j =1，2，…，n)的价值评定量，相应的关联矩阵见表1。

表1 备选点综合评价关联矩阵

评价:

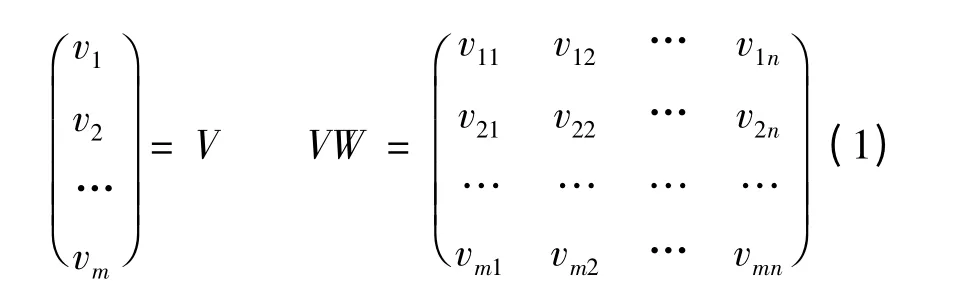
对于不同的评价指标，难以在同一标准下进行比较:交通方便的道路枢纽往往隐蔽条件较差，靠近前方的储备地点往往安全防护性差，便于物资供应点补充的地域往往又距离前送补充要点太远。在这种情况下，可用逐对比较法来对不同的评价指标加以权重，即利用所有评价指标对替代方案按照一定的基准进行评分，再利用加权的方法对替代方案的各种评价指标的评价值进行综合评价。

对评价指标进行两两比较，认为相对重要的指标得分定为1，相对不重要的得分定为0，进行比较后的评价指标权值见表2。

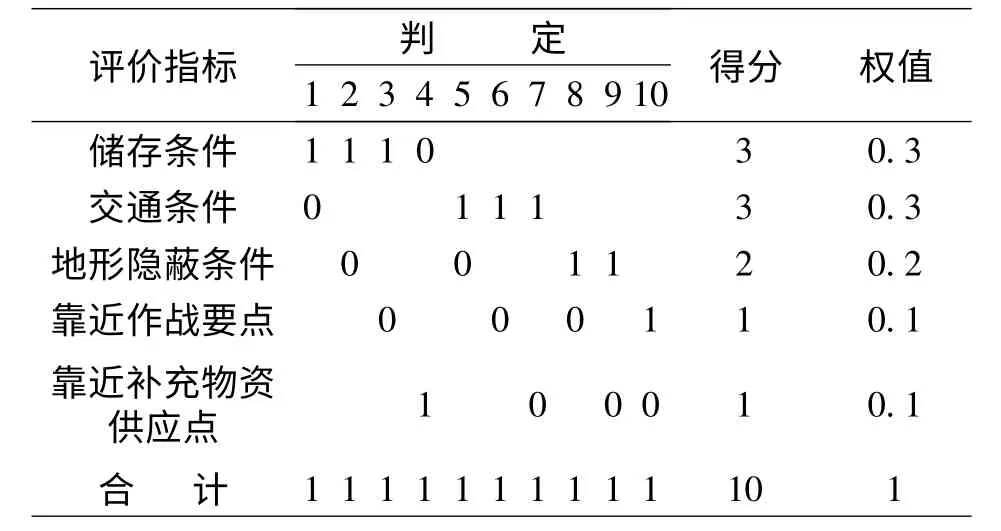
表2 用逐对比较法计算权重

得出评价指标的权重值后，再对各储备备选点进行综合评价，评价的标准分为好、一般、差三个等级，评价好的得分为2、评价一般的得分为1、评价差的不得分。例如，对8 个应急物资储备备选点b1，b2，…，b8 进行评价，见表3。

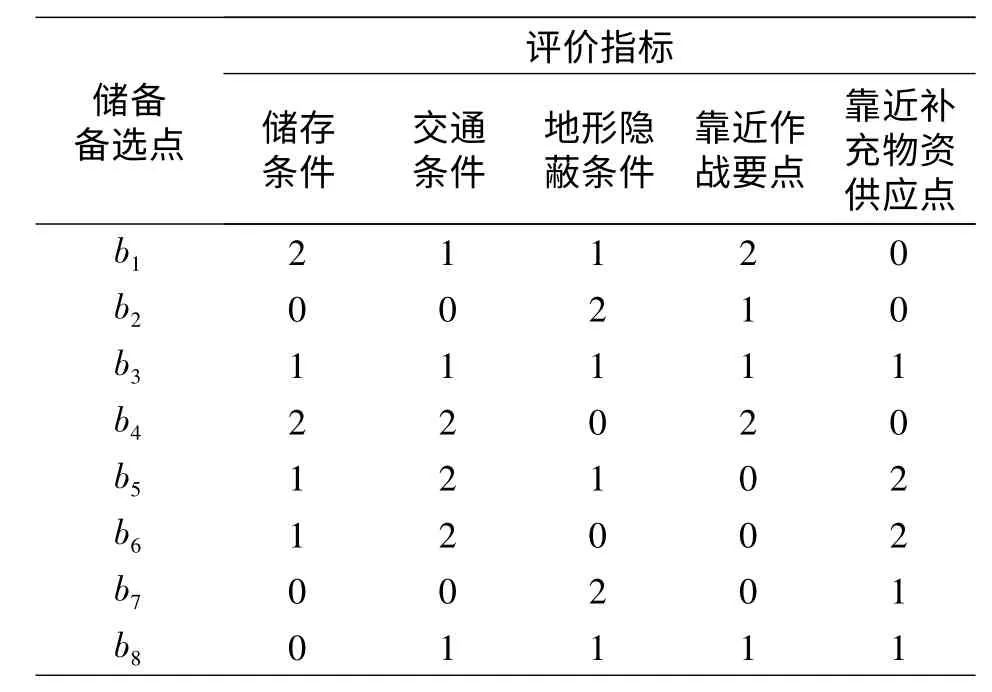
表3 备选点得分表

根据表3，各储备点得分为:

3.3 筛选备选点

根据以上对各备选点的综合评价，可以据此剔除一些不能满足应急物资储备要求的备选点，以减少后续模型计算的复杂性。如:现以评价得分1.0为划分标准，得分大于标准的可作为备选点，低于标准的不能作为备选点。这样，可以去掉b2、b7、b8三个不符合要求的备选点，保留剩余的五个备选点。

4 以单一目标对应急物资储备点进行优化

在应急物资储备点选址目标模型中，设定了最短距离、最短时间、调运成本、建设成本、储存数量五个目标，可以任意目标进行应急物资储备点优化。在本文中，仅以时间最短为目标进行应急物资储备优化为例，对单一目标优化展开说明。

该优化目标是应急物资从储备点输送到需求点的时间最短，这需要先算出各条线路的应急物资输送速度，再根据线路长度和平均输送速率，折算成标准里程(通过速度一致的里程)，通过比较标准里程的长短即可比较输送时间的长短，从而确定应急物资储备点的位置。

4.1 运距换算

储备点的布置，必须依托于运输方式的选择，无论采用何种运输方式，前送的时间要求是一致的。根据实际情况，应急物资输送主要有水路、铁路、公路这三种运输方式，其实际输送距离的长短并不能衡量出应急物资前送实际时间长短，这就无法比较不同运输方式条件下保障时效性的优劣。这需要结合各种运输方式条件下应急物资输送的速度、道路或水路的安全通过系数等因素具体分析，对实际输送距离进行运距的换算，折算成标准运距。标准运距越长，该运输方式下单位应急物资前送所需的时间越长，保障效益越差。设标准运距为S，实际运距为L，折算系数为d，则有S = Ld。

标准运距的折算系数d可根据下式得出:

式(2)中，V0为单位应急物资输送的标准速度(km/h);V为该输送方式下单位应急物资的实际运送速度(km/h);K为该输送方式的道路(水路)的地形修正系数，K≥1;U为该方式下安全通过系数，U≤1。

假如从储备点A到要点B的输送过程中经过道路换乘或输送方式转换，则可分段求取各路段的标准运距，再求和得出总的标准运距，即:

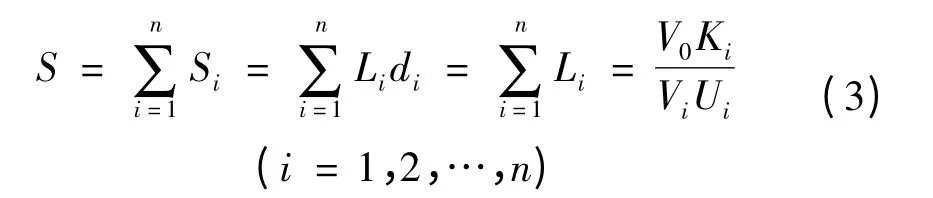
4.2 应急物资储备优化模型的建立

最短时间优化模型，设在某一作战方向上，作战要点分别为ai(i =1，2，…，n)，每个要点针对某一种物资的作战应急物资需求量分别为Yi(i =1，2，…，n)，则由选定的x个应急物资储备点bj(j =1，2，…，x)向作战要点运送应急物资，将实际运距进行标准运距折算后，用最短路方法计算后，设最小标准运距为Sji(i =1，2，…，n;j =1，2，…，x)，写成矩阵形式为:

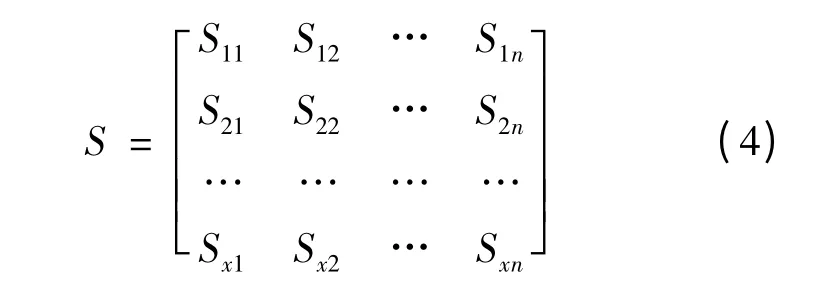
也可写成时间矩阵形式，即标准运距除以标准运送速度:

在该矩阵中，如果某一储备点不能到达某一需求点，可以设该段距离(时间)为∞，以简化矩阵。

4.3 储备方案分析

在上述矩阵中，可以很快找到一个储备点，使其到最远需求点的标准运距最短(时间最短)，该点即是所求的最优点。但这里的最优点是到最远需求点的标准运距最小，而不是总标准运距最小。也就是，到最远需求点的时间最少，而不是总时间最少。优化比较时，先从矩阵中提取每个储备点到所有需求点中的最大标准运距(时间)，再比较每个储备点的最大标准运距(时间)，选出标准运距最短(时间最少)的储备点。

如果需要确定多个储备点，则应根据需要确定的储备点个数，选取储备点组合，使得该储备点组合能到达所有需求点。该组合中，按照就近保障的原则，以组合中储备点到需求点标准运距(时间)最小来确定保障关系，再比较不同组合到最远需求点的最大标准运距(时间)，用时少者为最优。通过储备点组合之间的比较，可以得到最优的储备点方案。

4.4 应用举例

设在位置点b1、b2、b3、b4、b5中设置应急物资储备点，要保障作战方向上的7 个要点(a1，a2，…，a7)，各要点的应急物资需求量分别为Y1，Y2，…，Y7，储备点经通道至作战要点的最短时间(h)矩阵如下:

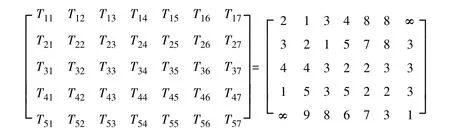
可以假设储备点至需求点的时间不能长于5h，即从储备点到保障要点的时间Tji≤5h，如果Tji ＞5h，则该储备点不能保障这个需求点。那么，时间矩阵可变为:

4.4.1 选择一个储备点

如果只选择一个储备点(能到达所有需求点)，则从矩阵中选出至最远保障点时间最短的一个点。矩阵中点b3至最远需求点的时间为4h，点b4至最远需求点的时间为5h，b3点应是时间最优的储备点。

4.4.2 选择两个以上储备点

如果选择两个以上的储备点，则要根据就近保障的原则区分保障任务。本文中，以选择两个储备点为例，可以选择的位置点组合有:b1和b3、b1和b4、b2和b3、b2和b4、b3和b4、b4和b5。

(1)当选择b1和b3为储备方案时，由b1保障a1、a2、a3，至最远需求点时间为3h;由b3保障a4、a5、a6、a7，至最远需求点时间为3h;该方案至最远需求点的时间为3h。

(2)当选择b1和b4为储备方案时，由b1保障a2、a3、a4，至最远需求点时间为4h;由b4保障a1、a5、a6、a7，至最远需求点时间为3h;该方案至最远需求点的时间为4h。

(3)当选择b2和b3为储备方案时，由b2保障a1、a2、a3、a7，至最远需求点时间为3h;由b3保障a4、a5、a6，至最远需求点时间为3h;该方案至最远需求点时间为3h。

(4)当选择b2和b4为储备方案时，由b2保障a2、a3、a4、a7，至最远需求点时间为5h;由b4保障a1、a5、a6，至最远需求点时间为2h;该方案至最远需求点时间为5h。

(5)当选择b3和b4为储备方案时，由b3保障a2、a3、a4、a5，至最远需求点时间为4h;由b4保障a1、a6、a7，至最远需求点时间为3h;该方案至最远需求点时间为4h。

(6)当选择b4和b5为储备方案时，由b4保障a1、a2、a3、a4、a5、a6，至最远需求点时间为5h;由b5保障a7，至需求点时间为1h;该方案至最远需求点时间为5h。

所以，当选择b1和b3或b2和b3为储备方案时，至最远储备点所花时间最短，它们是时间最优的储备方案。

5 以多目标决策方法进行应急物资储备优化

在实际应用中，物资储备点组合方案的选取标准不一，究竟该以哪一种目标作为最终的选取标准很难确定。不同优化目标方案之间往往会相互矛盾，如:距离前方近势必距离后方油源远，减少储备点势必造成单个储备点数量规模过大，等等。可考虑采用多目标决策方法，综合考虑物资储备点距离、时间、调运成本、建设成本、储备数量等因素，赋予不同的加权系数，比较得出物资储备优化方案。

5.1 建立模型

首先明确评价目标和建立评价指标，评价指标可以通过专家打分、综合评议的方式确立;备选方案可以通过决策者与相关专家会审确定。

5.2 统一标准

不同评价目标的计量单位标准不一，有距离、时间、成本、数量等，无法进行比较。因此，必须把这些计量单位数值转化为可比较的效用值来表示。效用值取0—1 之间的所有数，每个目标的最坏程度，效用值为0，低于最坏程度的舍弃;每个目标要求的最好程度，效用值取1，高于最好程度的同最好程度一样看待，取值为1。

为便于保障，利于安全，假设储备方案的几个目标应为:距需求点距离最好小于200km，最坏也不能超过500km;到需求点时间最好在12h 内，最坏也不能超过24h;物资调运总成本最好在3000 吨·百公里以下，最坏也不能超过6000 吨·百公里;物资储备点建设成本最好在5000 万元以下，最坏也不能超过6000 万元;物资储备总数量最好在1 万吨以下，最坏也不能超过2 万吨。这样可以画出各目标的效用曲线，并求得各方案中各目标的效用值大小。

5.3 淘汰劣案

作为备选方案，所有目标只要有一项是超出最坏程度的，作为劣案淘汰。

5.4 附加系数

在上述目标中，并不是所有的目标都具有同等重要性，因此需要考虑各个目标在优化中的重要程度并赋予适当的系数。将各方案目标的效应值乘以比重系数，然后相加得到总和，方案所得总和最大的就是最优方案。即:

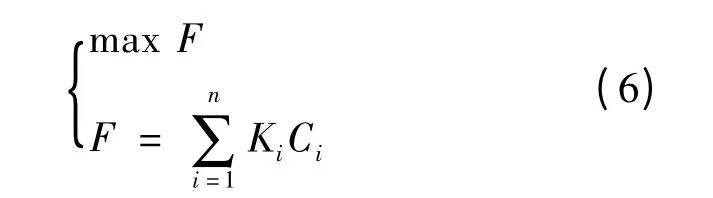
式(6)中，F为效用值函数，Ki为每个目标的效用值比重系数，Ci为评价目标。

5.5 应用举例

假设有储备布局方案P1、P2、P3，综合最短距离、最少时间、最小调运成本、最小建设成本和最少储存数量等优化目标进行物资储备的比较优化，五个优化目标的比重系数分别为2、3、3、1、1，三个储备方案的目标值见表4。

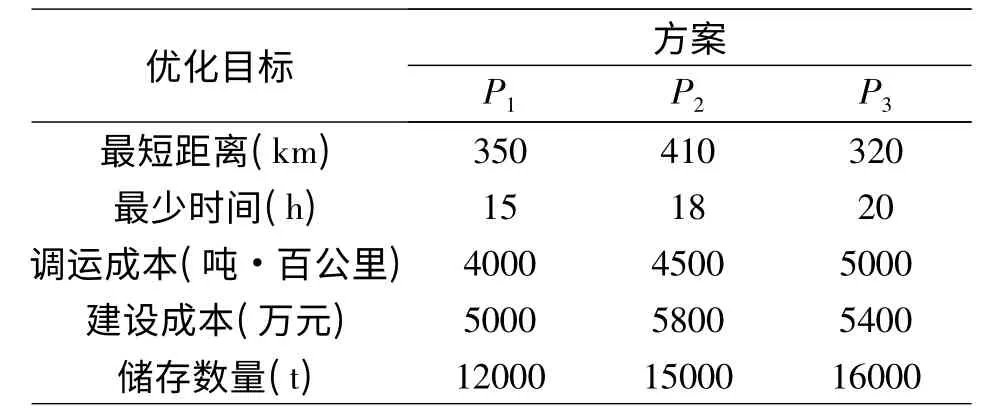
表4 储备布局方案目标值对比表

根据前文所设的效用值程度，进行效用值计算后所得见表5。

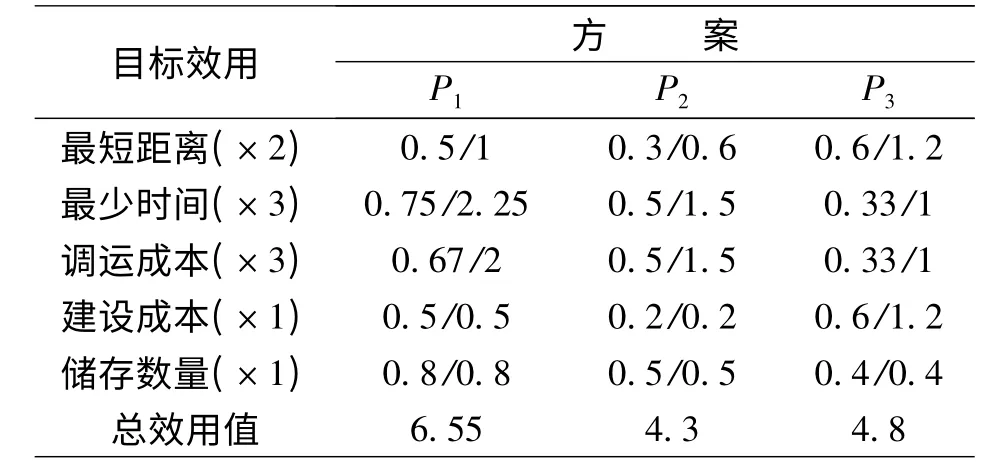
表5 储备布局方案效用值对比表

从表5 中可以看到，当采用方案P1时，多目标效用值最大，即取得最优的储备效能。所以多目标决策的优化结果是选择方案P1。

6 结束语

在应急物资储备点选址问题研究中，由于不同优化目标可能存在矛盾，一般没有全局最优解存在。本文建立的多目标优化模型，利用模糊逻辑的多目标遗传算法求解，能够达到比较好的效果。该模型曾被应用于部队军需物资油料保障系统中，可根据标定的保障方向、选择的参与保障单位、初始的保障任务以及用户设定的相关参数等，对军区油料储备布局进行优化分析，为战区的平时供应管理和战时保障的保障点选址提供决策参考，取得很好的军事和经济效益。

［1］ 张来顺，尚振峰，姚頔.联勤保障一线仓库布局优化分析［J］.火力与指挥控制，2011，36(1):37 -39.

［2］ 陈阳，雍岐东，邢兆勇，等.基于物联网的军队油料储备布局研究［J］.训练与科技，2013，34(3):4 -6.

［3］ 陈智，郭继坤.以线性规划方法构建油料储备布局模型［J］.后勤学术，2004(12):90 -92.

［4］ 双海军.战备物资储备优化［D］.重庆:后勤工程学院，2001.

［5］ 徐东.新形势下军事物资储备布局的合理性研究［D］.北京:后勤指挥学院，1999.

［6］ 郭继坤.战时物资勤务［M］.北京:军事科学出版社，2004.