赣南地区P波、S波随频率衰减关系研究*
汤兰荣,董非非,曾新福,项月文
(江西省地震局,江西南昌330039)
0 引言
Q值是量度地球介质对地震波衰减 (Q-1)的基本物理参数之一,是描述地壳介质非均匀程度的确定性指标 (Roecker et al.,1982),Q值的大小及其对频率的依赖程度反映了介质的非均匀性和非弹性特征,既包含介质对地震波能量的吸收,也包含了对地震波的散射,因此,不同的构造区有不同的衰减特性。由于品质因子与区域构造活动、地震活动密切相关,可以作为评价区域构造活动的基本指标,用以分析区域地震活动水平。
用于计算Q值的方法很多,目前国内外利用天然地震的体波、尾波、Lg波开展地壳介质品质因子Q值研究应用比较广泛的方法主要有:多台多震联合反演方法计算 S波衰减 (Atkinson,Mereu,1992;Singh et al.,1999;黄玉龙等,2003)、叠加谱比 (Xie,Mitchell,1990)、单次散射模型的尾波Q值计算方法 (Aki,Chouet,1975;Sato,1977)和尾波归一化方法 (Aki,1980;Sato,1980;Yoshimoto et al.,1993;Sharma et al.,2007;Lorenzo et al.,2013)等,李祖宁等(2012)利用Atkinson方法研究得出福建地区介质平均Q值与f的关系式。本文采用尾波归一化方法研究计算P波和S波的衰减,王勤彩等 (2005)首次利用此方法得到云南地区的P波、S波衰减规律,华卫等 (2009)和董非非等 (2013)分别对龙滩水库地区和赣西北地区P波、S波随频率的衰减关系进行了研究。
1 方法原理
Aki(1980)首先考虑通过一个记录中的S波谱振幅与尾波谱振幅之比,以消除震源和台站场地项,用S波尾波归一化方法得到日本关东地区与频率有关的S波衰减;Yoshimoto等 (1993)在上述研究的基础上,指出鉴于P波谱振幅与S波谱振幅成比例,假设在很小的震级范围,很窄的频带内,就可以把此方法扩展到P波,得到能同时测定P波、S波衰减的体波归一化方法。
对于地方震,在扣除了噪音、仪器响应和台站场地响应后,S波谱振幅为
式中,S(f,θ)为包含了震源辐射图像效应的震源谱,R代表震源矩,β表示S波速度。扣除噪音、仪器响应和台站场地效应后,对于地方震,尾波的振幅可用式 (2)表示 (Aki,Chouet,1975),只是这时S(f)仅为震源谱。
式中,tC为尾波的走时,即从地震发震时间算起至尾波测量的时间,一般tC>2R/β。
将式 (1)除以式 (2),并取对数,整理后得
为了消除震源辐射图像的影响,即消去上式右边的第一项,对展布在R±ΔR范围 (R不同,θ不同)的多个地震求平均,即对不同的R进行回归计算 (用< >表示),即有
根据式 (3),C(f,tC)仅是频率和走时tC的函数,与震源和台站的位置无关,故当对所有地震都取同样的走时tC时,则对某中心频率fK,lnC(fK,tC)为常数,这里令
“说来话长,民国24二十四年,随家父渡海来到厦门开办诊所,平常还从台湾倒一些洋药洋膏到大陆转卖,生意到也红火生意倒也红火。
在对地震记录滤波后,对各中心频点fK在S波窗和尾波窗 (对于每次地震,tC相同,在tC前后取一定长度的尾波记录)分别计算S波和尾波的均方根振幅,然后对式 (7),以R为变量,用最小二乘法进行回归计算,得到斜率b,从而得到
由一系列的QS(fK)即得到QS(f)=Q0fη。由于P波的谱振幅AP(f)与S波谱振幅AS(f)成正比,故有AP(f)~AC(f),于是用该方法也可求得P波的Q值QP(f)。
2 资料选取与处理
赣南“十五”数字地震台网于2007年10月开始投入运行,有数字地震台站7个,运行初期观测波形数据不够完整,2009年1月开始观测资料较齐全,因此选用2009年1月~2013年2月赣南及邻区ML≥1.0地震 (图1)进行研究。由于尾波归一化方法对地震数量和地震相对台站分布有一定要求,安远 (ANY)、龙南 (LON)和寻乌(XUW)3个台站周边地区小震活动较活跃,断裂构造发育,在赣南地区具有代表性,因此选这三个台站进行QP和QS研究。寻乌和龙南台地震计为KS-2000宽频带速度地震计 (平坦范围120 s~50 Hz),安远台地震计为BBVS-60宽频带速度地震计 (平坦范围60 s~40 Hz),3个台站数采型号均为EDAS-24IP,采样率为100 sps。
对台站和地震初步选定后,首先在5个不同频带范围内利用巴特沃斯带通滤波器进行滤波,在此基础上,选取尾波信号大于2倍噪声的地震计算每个台站的尾波归一化值,由于地震到各台站的距离不相同,每个台站选取的尾波结束的流逝时间也不一样,3个台站选用的流逝时间在21~40 s之间,求出每个台站的QP、QS后,再计算拟合平均值。
3 计算结果与分析
表1、2给出了寻乌、安远和龙南台各频带的P波、S波衰减值、所用地震数以及衰减与频率关系的拟合结果。图2以寻乌台为例展示了各频带上经尾波归一化后S波振幅与震源距关系,图3给出了该台站得到的S波Q值拟合曲线,图中显示Q值随频率增大而增大,Q值与频率呈现较强的依赖关系。
由于计算方法对地震相对台站的分布和波形信噪比要求较高,挑选出来参与计算的地震波形数远远少于准备的基础波形资料。计算安远台采用的流逝时间均为21 s,由于多数地震距离龙南台更远,所以龙南台QP和QS流逝时间值取值更大,均为40 s。为了保证拟合质量,寻乌台计算QP和QS选用的流逝时间不同,计算QP的流逝时间为35 s,和龙南台相近,计算QS的流逝时间为21 s,和安远台相同。

表1 3个台站各频带的P波Q值结果 (M L≥1.0)Tab.1 Q value of P wave at different frequencies of three seismic satations(M L≥1.0)

表2 3个台站各频带的S波Q值结果 (M L≥1.0)Tab.2 Q value of Swave at different frequencies of three seismic stations(M L≥1.0)
流逝时间的大小对于Q值有一定影响,选取寻乌台QS计算结果为例,随着流逝时间的增大,S波尾波归一化Q0值有逐渐增大的趋势 (表3),6个流逝时间对应的P波Q0中,有一个点偏离这种趋势,去掉该点后拟合结果线性关系较好 (图4)。由此可以推断表1中安远台P波Q0值明显低于龙南和寻乌台的Q0值,可能与选用的流逝时间明显小于寻乌和龙南台,从而导致选用地震的震中距范围较小有关。表2中龙南台QS值明显大于寻乌台和安远台的QS值,可能是与龙南台选取的流逝时间较大,从而选用地震震中距范围较大有关。
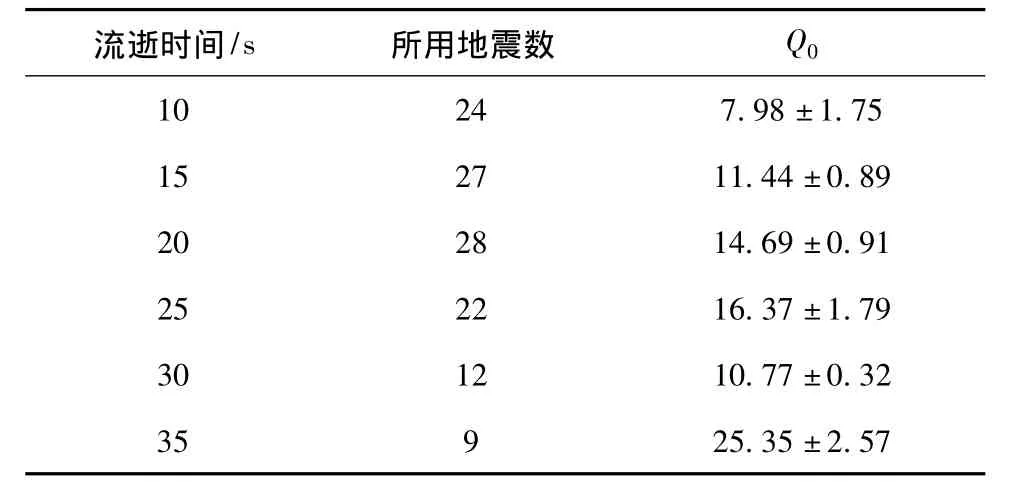
表3 寻乌台不同流逝时间对应的S波尾波归一化Q0值Tab.3 Q0 value for Swave in different lapse time derived by using the extended coda-normalization method at Xunwu Station
对于Q值平均值的计算,考虑到流逝时间对结果的影响以及各台站拟合结果的可靠性,选用流逝时间相近的寻乌台 (35 s)和龙南台 (40 s),将各频点的P波Q值平均后重新拟合,得到寻乌龙南地区的P波平均Q值QP(f)=(20.76+1.67)*f(1.03±0.04);选用流逝时间相同的寻乌台和安远台(21 s),将各频点的S波Q值平均后重新拟合,得到寻乌安远地区的S波平均Q值QS(f)=(18.86+1.46)*f(0.84±0.04)(图5)。P波与S波平均Q值接近,QP略大可能与流逝时间选择不同有一定关系。参与平均值计算的台站各频点对应的Q值比较相近,反映了上述结果的可靠性。
4 结论与讨论
使用扩展的尾波归一化方法要求研究区内有较多的地震且分布均匀,以消除辐射花样和入射角的影响;另外要求尾波信号大于2倍噪声 (王勤彩等,2005),为了保证计算地震的样本数和拟合精度。本文对寻乌、安远和龙南台进行尾波归一化Q值计算时,QP和QS计算选取流逝时间不完全一致,但参与平均值拟合的不同台站选取流逝时间接近或相同,尽量减小由于流逝时间不同而产生的Q值差别,因为流逝时间的长短直接影响所用资料的震中距范围,而Q0值的高低与所用资料震中距离的范围有关 (Dinesh et al.,2005,2006;Sharma et al.,2007)。计算寻乌台 S波 Q值时,选用6个不同流逝时间进行Q0值对比发现流逝时间与Q0值大小具有线性关系 (表3,图4)。从图5可以看出参与QP或QS平均值拟合的流逝时间相近的台站QP或QS值都较接近,特别是流逝时间相同的寻乌台和安远台,其QS值更加接近,因为这两个台站相距仅28 km,计算选择的地震波形穿透的区域有部分重叠。最终得出的寻乌龙南地区的P波平均Q值比寻乌安远地区的S波平均Q值略大一些,与某些QS/QP>1的研究结果 (华卫等,2009;Sharma et al.,2007)有所不同,原因是采用平均值计算的台站不完全相同,且计算QP选取的流逝时间更大。
本研究中得到的P波、S波的Q0值不高,分别为20.76、18.86,与赣西北地区相同方法计算QP和QS值 (董非非等,2013)所用资料的震中距离相近,Q值结果相差不大。比华卫等 (2007)对龙滩水库地区的计算结果高,造成这种现象的原因除了区域介质均匀程度不同造成数值差别以外,另外一个原因是本文研究区域比龙滩水库地区计算所用资料的震中距要大。本文未参与QP值平均值拟合的安远台选用的地震震中距范围就相对较小,因此QP值明显低于寻乌和龙南台 (表1)。最终P波、S波Q值平均值结果η值较高,分别为1.03和0.84,说明QP和QS值与频率的依赖程度较高,本文所使用的地震资料的震源深度大部分在4~11 km之间,高η值反映了地壳浅层介质非均匀性较高,与华卫等 (2007),董非非等(2013)研究结果相似。赣南地区受台湾板块边界带强震活动直接影响,是华南内陆地震活动水平较高的地区,区内1500年以来发生4■4级以上地震10次,最大地震为1806年1月11日会昌6级地震,1980年以来也发生了1982年2月龙南5.0级地震、1987年8月寻乌5.5级强震群和一系列的4级以上显著地震,沿河源—邵武断裂带、南岭纬向构造带温泉广泛分布,非常发育 (何昭星,1989)。本研究得到该地区的Q值结果总体呈现低Q0和高η值的特点,是构造运动活跃地区的特征体现,和上述地震活动实况是较为吻合的。
本文所用程序由中国地震局地震预测研究所华卫博士提供,他在理论与方法上给予诸多指导和帮助,在此深表谢意。
董非非,汤兰荣,潘林山,等.2013.赣西北地区P波S波随频率衰减关系研究[J].大地测量与地球动力学,33(增刊I):97-105.
何昭星.1989.江西寻乌震区地震地质特征初步研究[J].华南地震,9(2):14-21.
华卫,赵翠萍,陈章立,等.2009.龙滩水库地区P波、S波和尾波衰减[J].地震学报,23(6):620-628.
黄玉龙,郑斯华,刘杰,等.2003.广东地区地震衰减和场地响应的研究[J].地球物理学报,46(1):54-61.
李祖宁,杨贵,陈光.2012.福建地区地震波大弹性衰减Q值场地响应及震源参数研究[J].地震研究,35(2):381-386.
王勤彩,刘杰,郑斯华,等.2005.云南地区与频率有关的P波、S波衰减研究[J].地震学报,27(6):588-597.
Aki K.,Chouet B..1975.Origin of Coda Waves:Source,Attenuation and Scattering Effects[J].J.Geophys Res.80(23):3322-3342.
Aki K..1980.Attenuation of Shear Waves in the Lithosphere for Frequencies from 0.05 to 25 Hz[J].Phys.Earth Planet,21(1):50-60.
Atkinson G.M.,Mereu R.F..1992.The Shape of Ground Attenuation Curves in Southeastern Canada[J].Bull.Seism.Soc.Amer.,82(5):2014-2031.
Dicesh K.,Sriram V.,Khattri K.N..2006.A Study of Source Parameters,Site Amplification Functions and Average Effective Shear Wave Quality Factor Qseff from Analysis of Accelerograms of the 1999 Chamoli Earthquake,Himalaya[J].Pure Appl Geophys,163:1369-1398.
Dinesh K.,Sarkar I.,Sriram V.,et al..2005.Estimation of the Source Parameters of the Himalaya Earthquake of October 19,1991,Average Effective Shear Wave Attenuation Parameter and Local Site Effects from Accelerograms[J].Tectonophysics,407:1-24.
Lorenzo S.D.,Bianco F.,Pezzo E.D..2013.Frequency Dependent QSand QPin the Umbria-Marche(Italy)region using a Quadratic Approximation of the coda-Normalization Method[J].Geophys J.Int.,193:1726-1731.
Roecker S.W.,Tucker B.,King J.,et a1..1982.Estimation of in Central Asia as a Function of Frequency and Depth using the Coda of Local Recorded Earthquakes[J].Bull.Seism.Soc.Amer.,72:129-149.
Sato H..1977.Energy Propagation Including Scatter1ng Effects:Single I-sotropic Scattering Approximation[J].J.Phys.Earth,25:27-41.
Sato H..1980.Q-1Value for S-wave under the Kanto District in Japan[J].Zisin,33:541-543.
Sharma B.,Teotia S.S.,Kumar D..2007.Attenuation of P,S,and Code Waves in Koynaregion,India[J].J.Seismol.,11:327-344.
Singh S.K.,Ordaz M.,Dattatrayam R.S..1999.A Spectral Analysis of the 21 May 1997 Jabalpur India,Earthquake and Estimation of Ground Motion from Future Earthquakes in the India Shield Region[J].Bull.Seism.Soc.Amer.,89(6):1620-1830.
Xie J.,Mitchell B.J..1990.A back Projection Method for Imaging Largescale Lateral Variation of Lg coda Q with Application to Continental Africa[J].Geophys J.Int.,100(1):161-181.
Yoshimoto K.,Sato H.,Yoshihisa,et al..1993.Frequency-dependent Attenuation of P and S Waves in the Kanto area,Japan,Based on the Coda-normalization Method[J].Geophys J.Int.,114:165-174.

