摆杆和摆杆座质量对复摆实验的影响
段益峰,秦丽霞,于建勇
(中国矿业大学,江苏徐州 221116)
复摆又称为物理摆,是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系。通过对复摆物理模型的分析,可以用来测量重力加速度和转动惯量以及验证平行轴定理等等[1-3]。复摆的结构形式有多种,图1a~c图3所示是3种常见的结构形式不同的复摆。

图1 复摆示意图

如图1(a)所示,刚体绕固定轴O在竖直平面内作左右摆动,G是该物体的质心,与轴O的距离为h,θ为其摆动角度。若规定右转角为正,此时刚体所受力矩与角位移方向相反,即有

又据转动定律,该复摆又有

其中I为该物体转动惯量。由公式(1)和(2)可得

其中ω2=。若θ很小时(θ在5°以内)近似有

此方程说明该复摆在小角度下作简谐振动,该复摆振动周期为

利用平行轴定理,设IG为转轴过质心且与O轴平行时的转动惯量,则有

因此,有

根据公式(7)可测重力加速度。
1 复摆为固定刚体时的实验方案
对于固定的刚体而言,IG是固定的,因而测量重力加速度时,只需改变质心到转轴的距离。设质心离O轴的距离分别为h1和h2,对应周期分别为T1和T2,为使计算简化,取h2=2h1,则

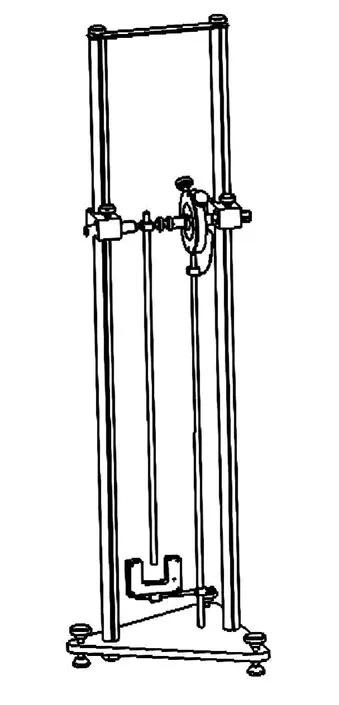
图2 复摆装置
测量两组数据,即可求出重力加速度值。如图1a所示装置,如果摆杆为轻质摆杆,质量相对摆锤可以忽略,则复摆质心始终在摆锤质心,只需要改变摆锤位置,就可以改变质心到复摆转轴的距离,则公式(8)显然成立。如图1b所示装置,通过刀刃悬挂的复摆,可以通过改变刀刃的悬挂位置,改变复摆质心到转轴的距离,在改变质心到转轴距离的过程中,复摆是一个固定刚体,其相对过质心且平行于悬挂点的转轴的转动惯量是固定值,因此公式(8)也成立[4],可以用来测量重力加速度。
2 非固定刚体的复摆装置的实验方案
如图1a,如果摆杆质量不能忽略,复摆质心位置由摆杆和摆锤共同决定,对摆杆和摆锤共同组成的刚体并非固定刚体,则公式(8)并不成立[5-6]。如图2所示的复摆装置,摆杆为铁质摆杆,摆杆质量ml=620 g。转轴处采用摆杆座固定摆杆,摆杆可在摆杆座内滑动以调节刚体重心的高度,为防止生锈摆杆座采用钢材制作,摆杆座质量mo=60 g,摆杆上还可以安装可调节位置的摆锤,通过调节摆杆座和摆锤的位置可以改变复摆的质心到转轴的距离。在本装置中,移动摆杆座和摆锤的位置,则复摆就不是固定刚体,转轴过质心且与O轴平行时复摆的转动惯量IG将随着摆杆座和摆锤移动而改变,公式(8)不再成立。因此重新设计实验方案如下:
由于摆杆质量分布均匀,对于匀质摆杆,其质心位于摆杆中心。摆杆座的存在使质心位置发生改变,若在摆杆上安装一个摆锤,摆锤质量mo与摆杆座质量ma相等,均为60 g,若令摆杆座和摆锤相对摆杆中心对称安置,如图1c,则复摆系统质心仍在摆杆中心,如此问题可以简化。
根据平行轴定律可知,复摆的转动惯量

其中IG为包括摆杆座、摆杆和摆锤三者相对过各自质心且与O轴平行的转轴的转动惯量之和,ml为摆杆质量,ma为摆锤质量,h为摆杆中心到摆杆座中心的距离。
将公式(9)代入(5)得复摆振动周期为
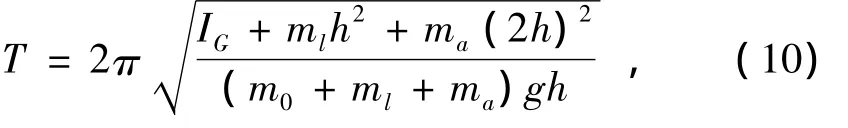
其中M=m0+ml+ma为摆杆座、摆杆和摆锤的总质量,即复摆的总质量。
使摆杆做微小摆动(摆角θ在5°以内),用多功能微秒计测出10个周期的时间Δt10(s),然后,保持摆杆座和摆锤相对摆杆中心对称,移动摆杆座和摆锤改变质心到转轴的距离h,并测出摆杆摆动10个周期的时间,测量多组数据,然后计算出周期,利用公式(10)即可求出重力加速度的值,相关数据如表1所示[7-8]。

表1 测复摆的振动周期
由公式10变换得线性关系式
h2=,经过线性拟合得
h2=0.2136T2h - 0.0287 则 g=0.2136=9.800037027 m/s2,实验结果合理。
3 结 论
复摆实验装置结构不同,所依据的原理就不同,要充分考虑到复摆各部分在刚体定轴转动时转动惯量对测量的影响。本文中,针对摆杆座和摆杆质量都较大的情况,分析了摆杆座和摆杆对实验的影响,提出了利用现有实验装置测量重力加速度的优化方案,并利用该方案进行了测量,实验结果合理。
[1]程守洙,江之永.普通物理学[M].北京:高等教育出版社,2008.
[2]代伟.复摆实验装置研究[J].实验技术与管理,2007,24(6):55-58.
[3]安爱芳,王玉清,任新成,等.加配重复摆振动周期的实验研究[J].大学物理,2003,22(10):28-31.
[4]陈思佳,张文霞,杨启凤,等.线性回归法和Matlab在复摆测重力加速度实验中的应用[J].物理实验,2009,29(3):44-46.
[5]张天洋,王艳辉,曲光伟,等.空气阻力对复摆振动周期的影响[J].物理实验,2008,28(11):42-45.
[6]毛瑞全,刘翠红,郑卿.复摆方程的一种求解方法[J].物理实验,2008,28(3):45-46.
[7]张凯,姚宇峰,刘紫,等.基于偏弱器h0复摆设计与实验研究[J].大学物理实验,2014,05:23-26.
[8]吴波,朱瑜.三线摆转动角度控制装置的设计[J].大学物理实验,2013,02:31-32.

